【数据结构】树的概念以及二叉树
目录
1 树概念及结构
1.1 树的概念
1.3 树的存储
2 二叉树的概念及结构
2.1 概念
2.2 特殊的二叉树
2.3 二叉树的性质
2.4 二叉树的存储结构
1 树概念及结构
1.1 树的概念
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。树有以下三个比较显著的特征:
- 有一个特殊的结点,称为根结点,根节点没有前驱结点
- 除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
- 树是递归定义的
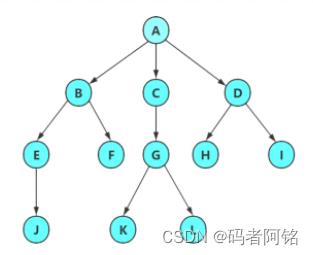
注意: 树形结构中,子树之间不能有交集,否则就不是树形结构
1.2 树的相关概念
- 节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
- 叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点
- 非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G...等节点为分支节点
- 双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
- 孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
- 兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
- 树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
- 节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
- 树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
- 堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
- 节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
- 子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
- 森林:由m(m>0)棵互不相交的树的集合称为森林;
1.3 树的存储
树结构相对线性表逻辑欢喜复杂很多,既需要保存值域,也要保存结点和结点之间的关系。所以不能以存储线性表的逻辑去看待树的存储。
实际中树有很多种表示方式如:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。
下图是一种最为直白的表示方式,即对于每一个节点,结构内定义多个孩子指针指向子节点。下列的每个指针也可以用一个指针数组来维护。但是由于孩子节点的数目是浮动变化的,这样做其实会造成很多资源的浪费。
如果明确了树的度,那么确实可以使用这种方法,但是由于每个节点的度并不一定一致,会造成很多资源的浪费。
可以使用顺序表代替静态数组来解决上述问题,但即使使用了顺序表,树的整个结构仍然过于繁琐。并不便于执行相关的操作。
应用比较广泛的是左孩子右兄弟表示法,即每个结点结构内控制指针只有两个。一个指针永远指向其每个孩子中最左边的孩子(树形逻辑结构中最左边的孩子),而另一个指针指向它右边第一个兄弟结点。
typedef int DataType; struct Node {struct Node* _firstChild1; // 第一个孩子结点struct Node* _pNextBrother; // 指向其下一个兄弟结点DataType _data; // 结点中的数据域 };
2 二叉树的概念及结构
2.1 概念
一棵二叉树是结点的一个有限集合,该集合:
- 或者为空
- 由一个根节点加上两棵别称为左子树和右子树的二叉树组成
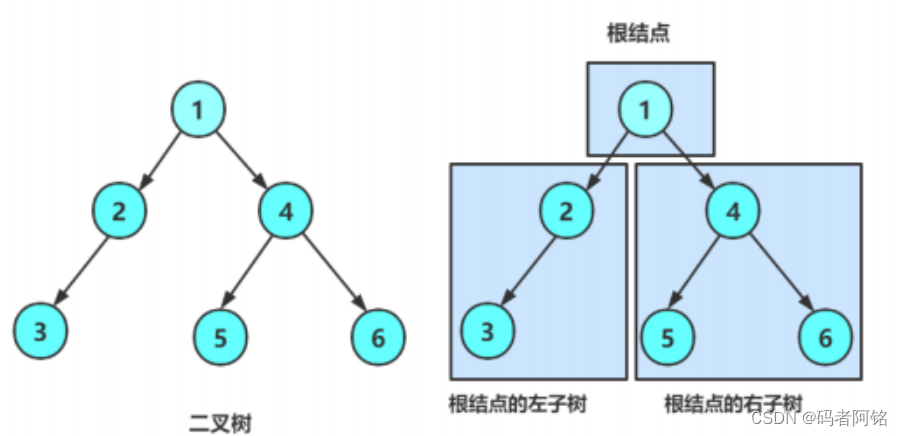
从上图可以很明显的看出:
- 二叉树不存在度大于2的结点
- 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
2.2 特殊的二叉树
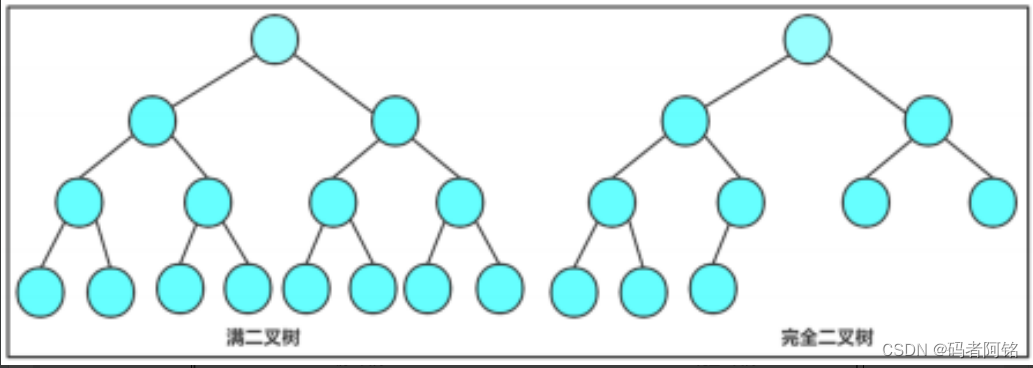
- 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是 说,如果一个二叉树的层数为K,且结点总数是 2^k-1,则它就是满二叉树。
- 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K 的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对 应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
2.3 二叉树的性质
二叉树有如下一些重要的性质:
- 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2^(i-1)个结点.
- 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2^h-1
- 对任何一棵二叉树, 如果度为0其叶结点个数为n0, 度为2的分支结点个数为n2,则有n0=n2+1
- 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h=log2(n+1)
- 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对 于序号为i的结点有:
若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点;
若2i+1<n,左孩子序号:2i+1,若2i+1>=n则无左孩子;
若2i+2<n,右孩子序号:2i+2,若2i+2>=n则无右孩子
2.4 二叉树的存储结构
二叉树一般可以使用两种结构存储,一种顺序结构,一种链式结构。
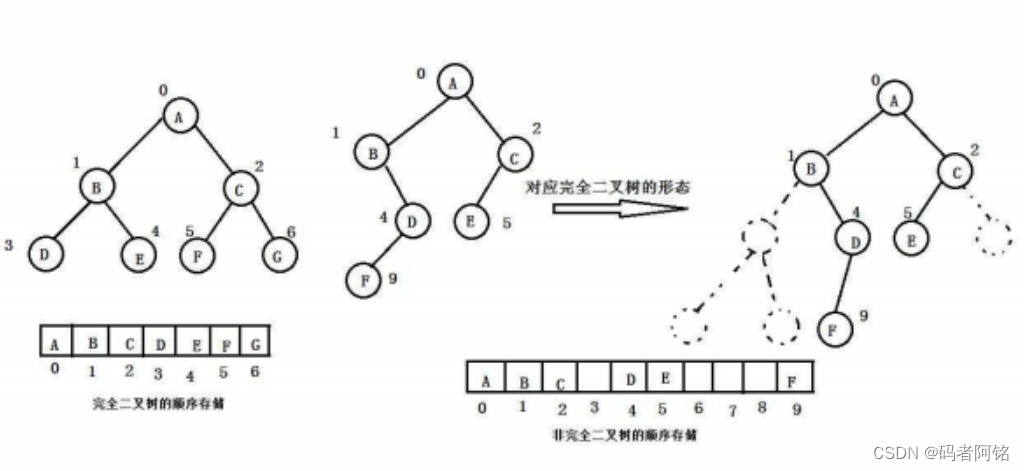
顺序存储顺序结构存储就是使用数组来存储 ,一般使用数组 只适合表示完全二叉树 ,因为不是完全二叉树会有空间的浪费。而现实中使用中只有堆才会使用数组来存储,关于堆我们后面的章节会专门讲解。二叉树顺 序存储在物理上是一个数组,在逻辑上是一颗二叉树。
链式存储二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。通常的方法是:链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址 。链式结构又分为二叉链和三叉链。三叉链比较复杂,在高阶数据结构如红黑树等会用到三叉链。
相关文章:
【数据结构】树的概念以及二叉树
目录 1 树概念及结构 1.1 树的概念 1.3 树的存储 2 二叉树的概念及结构 2.1 概念 2.2 特殊的二叉树 2.3 二叉树的性质 2.4 二叉树的存储结构 1 树概念及结构 1.1 树的概念 树是一种非线性的数据结构,它是由n(n>0)个有限结点组…...
软件测试职业规划导图
公司开发的产品专业性较强,软件测试人员需要有很强的专业知识,现在软件测试人员发展出现了一种测试管理者不愿意看到的景象: 1、开发技术较强的软件测试人员转向了软件开发(非测试工具开发); 2、业务能力较强的测试人员转向了软件…...
360压缩安装一半不动了?一分钟解决!
360压缩软件是我们常用的压缩软件,但是常常会遇到压缩安装到一半停止的情况,下面提供了一些可能的原因和解决办法,大家可以进行尝试~ 方法一:关闭防火墙和杀毒软件 有时候,防火墙和杀毒软件可能会阻止360压缩的安装过…...
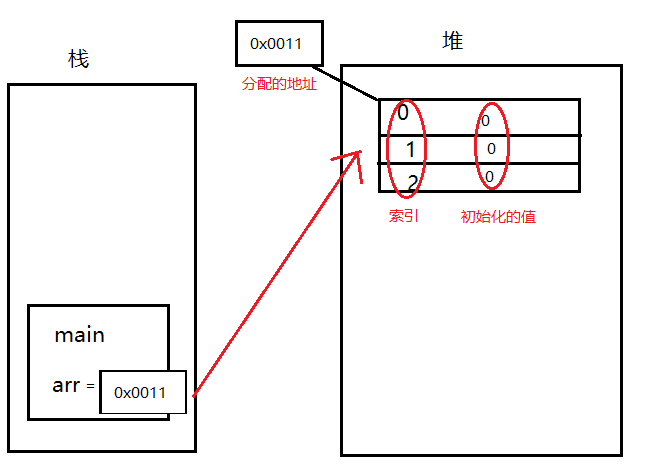
堆和栈的区别 重点来说一下堆和栈;堆与栈之间的联系
文章目录 堆和栈的区别重点来说一下堆和栈:那么堆和栈是怎么联系起来的呢? 堆与栈的区别 很明显: 今天来聊一聊java中的堆和栈,工作当中这两个也是经常遇到的,知识我们没有去注意理论上的这些内容,今天就来分享一下。…...

python 批量将图片存入excel单元格内
python 批量将图片存入excel单元格 示例代码1示例代码2 示例代码1 https://blog.csdn.net/wuyoudeyuer/article/details/128185284 # -*- coding: utf-8 -*- # Time : 2022-12-05 # Author : Carl_DJ 实现功能:在excel中,对应的名称后面,…...

Nginx常见的中间件漏洞
目录 1、Nginx文件名逻辑漏洞 2、Nginx解析漏洞 3、Nginx越权读取缓存漏洞 这里需要的漏洞环境可以看:Nginx 配置错误导致的漏洞-CSDN博客 1、Nginx文件名逻辑漏洞 该漏洞利用条件有两个: Nginx 0.8.41 ~ 1.4.3 / 1.5.0 ~ 1.5.7 php-fpm.conf中的s…...

Linux C语言 27-递归
Linux C语言 27-递归 本节关键字:C语言 递归 相关C库函数:main、printf 什么是递归? 在C语言中,程序调用自身的编程技巧称为递归(recursion)。递归从字面上可以理解为“递去归来”。 使用递归的优缺点 …...

redis运维(二十一)redis 的扩展应用 lua(三)
一 redis 的扩展应用 lua redis加载lua脚本文件 ① 调试lua脚本 redis-cli 通过管道 --pipe 快速导入数据到redis中 ② 预加载方式 1、错误方式 2、正确方式 "案例讲解" ③ 一次性加载 执行命令: redis-cli -a 密码 --eval Lua脚本路径 key …...

如何科学地划分医学图像数据集
在进行医学图像分类任务时,如何科学地划分数据集是一个重要的问题。这个问题的答案取决于你的数据特性和实验目标。一般来说,有两种常见的数据划分方法:按照比例划分和按照病例划分。 按照比例划分 按照比例划分是一种常见的方法,…...

【开源】基于Vue+SpringBoot的食品生产管理系统
项目编号: S 044 ,文末获取源码。 \color{red}{项目编号:S044,文末获取源码。} 项目编号:S044,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 加工厂管理模块2.2 客户管理模块2.3…...

如何减少40%的Docker构建时间
随着Docker的普及,许多公司的产品会将组件构建为Docker镜像。但随着时间的推移,一些镜像变得越来越大,对应的CI构建也变得越来越慢。 如果能在喝完一杯咖啡的时间(不超过5分钟)内完成构建,将是一个理想状态…...
Scrapy爬虫异步框架之持久化存储(一篇文章齐全)
1、Scrapy框架初识(点击前往查阅) 2、Scrapy框架持久化存储 3、Scrapy框架内置管道(点击前往查阅) 4、Scrapy框架中间件(点击前往查阅) Scrapy 是一个开源的、基于Python的爬虫框架,它提供了…...
JVM——几种常见的对象引用
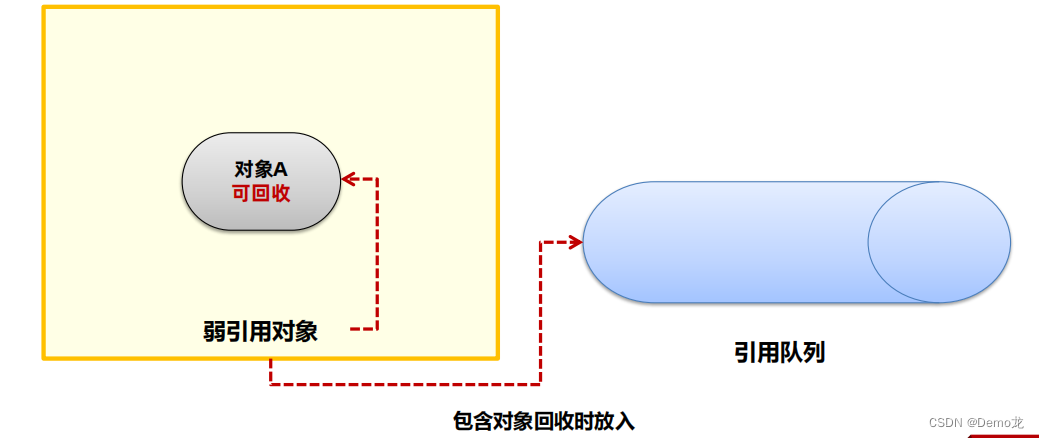
目录 1. 软引用软引用的使用场景-缓存 2.弱引用3.虚引用和终结器引用 可达性算法中描述的对象引用,一般指的是强引用,即是GCRoot对象对普通对象有引用关系,只要这层关系存在, 普通对象就不会被回收。除了强引用之外,Ja…...

C++期末考试选择题题库100道C++期末判断题的易错知识点复习
今天备考C,看到了一些好的复习资料,整合一起给大家分享一下 选择题 对于常数据成员,下面描述正确的是 【 B 】 A. 常数据成员必须被初始化,并且不能被修改 B. 常数据成员可以不初始化,并且不能被修改 C. 常数据成…...

使用qemu调试arm内核
参考书籍《奔跑吧Linux内核》–笨叔 下载Linux-5.0源码 https://benshushu.coding.net/public/runninglinuxkernel_5.0/runninglinuxkernel_5.0/git/files或者直接git源码 git clone https://e.coding.net/benshushu/runninglinuxkernel_5.0/runninglinuxkernel_5.0.git安装必…...

Pytorch深度学习实战2-1:详细推导Xavier参数初始化(附Python实现)
目录 1 参数初始化2 Xavier参数初始化原理2.1 前向传播阶段2.2 反向传播阶段2.3 可视化思考 3 Python实现 1 参数初始化 参数初始化在深度学习中起着重要的作用。在神经网络中,参数初始化是指为模型中的权重和偏置项设置初始值的过程。合适的参数初始化可以帮助模型…...

Java的threadd常用方法
常用API 给当前线程命名 主线程 package com.itheima.d2;public class ThreadTest1 {public static void main(String[] args) {Thread t1 new MyThread("子线程1");//t1.setName("子线程1");t1.start();System.out.println(t1.getName());//获得子线程…...
一键修复0xc000007b错误代码,科普关于0xc000007b错误的原因
最近很多用户都有遇到过0xc000007b错误的问题,出现这样的问题想必大家都会手足无措吧,其实解决这样的问题也有很简单的解决方法,这篇文章就来教大家如何一键修复0xc000007b,同时给大家科普一下关于0xc000007b错误的原因࿰…...
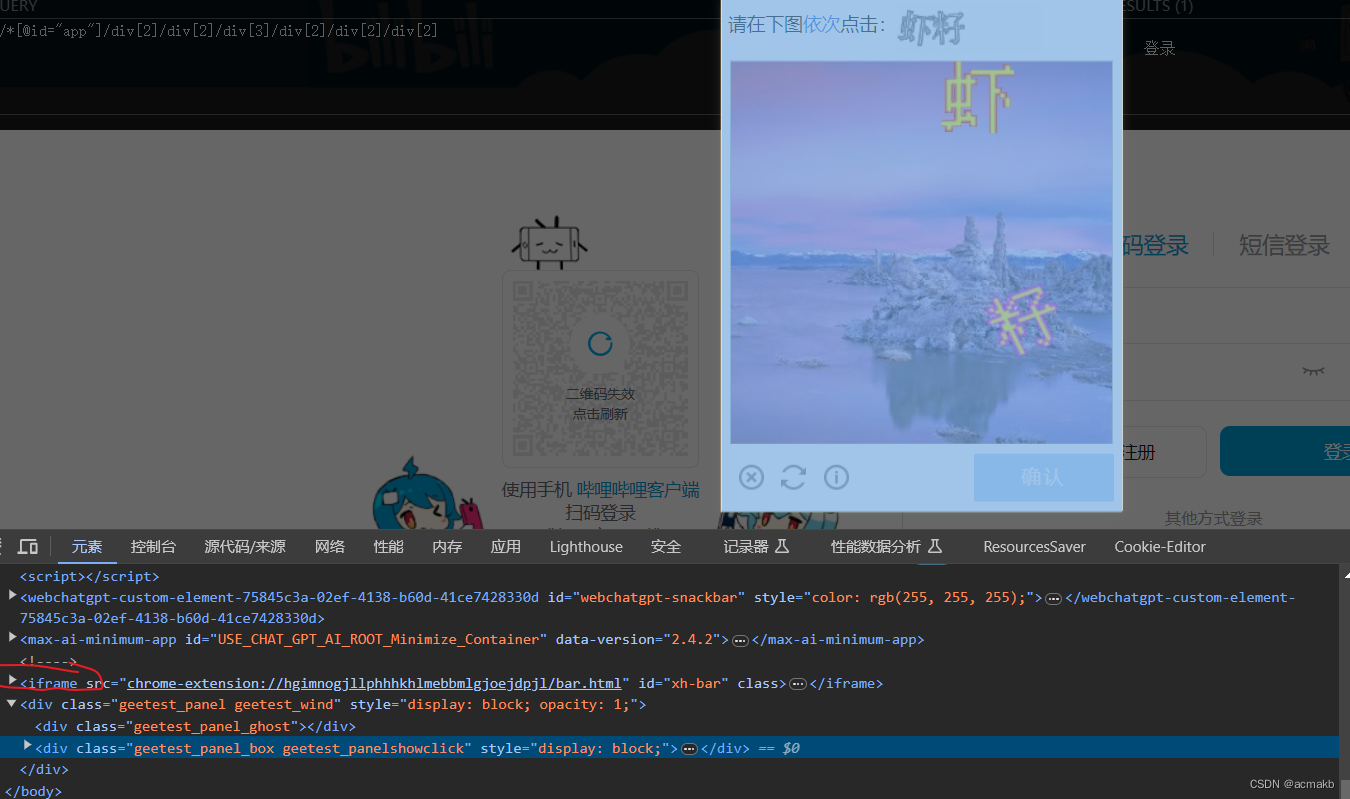
使用Selenium、Python和图鉴打码平台实现B站登录
selenium实战之模拟登录b站 基础知识铺垫: 利用selenium进行截图: driver.save_screenshot() 注意图片文件名要用png结尾. 关于移动: ActionChains(bro).move_to_element_with_offset()# 对于某个图像ActionChains(bro).move_by_offset(…...

嵌入式设备视频编码比较:H.264、H.265、MPEG-2和MJPG
在嵌入式设备领域,视频编码是一项关键技术,它能够将高清视频压缩为更小的数据量,以实现高效的存储和传输。本文将对四种常见的视频编码标准进行详细比较,包括H.264(AVC)、H.265(HEVC)…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...