力扣日记11.27-【二叉树篇】二叉树的最大深度
力扣日记:【二叉树篇】二叉树的最大深度
日期:2023.11.27
参考:代码随想录、力扣
104. 二叉树的最大深度
题目描述
难度:
给定一个二叉树 root ,返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。
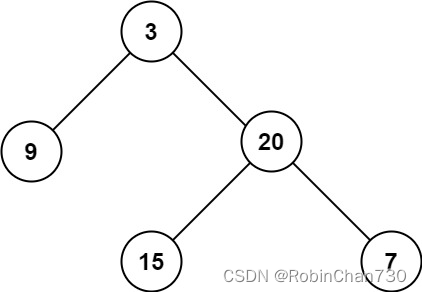
示例 1:
输入:root = [3,9,20,null,null,15,7]
输出:3
示例 2:
输入:root = [1,null,2]
输出:2
提示:
- 树中节点的数量在 [0, 10^4] 区间内。
- -100 <= Node.val <= 100
题解
递归法(cpp ver)
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:// 递归法:后序遍历 (实际上是求高度)// 1. 确定递归函数的参数和返回值:参数就是传入树的根节点,返回就返回以该节点为根的树的深度int getdepth(TreeNode* node) { // 2. 确定终止条件:如果为空节点的话,就返回0,表示高度为0。if (node == NULL) return 0;// 3. 确定单层递归的逻辑:先求它的左子树的深度,再求右子树的深度,最后取左右深度最大的数值 再+1 (加1是因为算上当前中间节点)就是目前节点为根节点的树的深度。int leftdepth = getdepth(node->left); // 左(左子树的高度)int rightdepth = getdepth(node->right); // 右(右子树的高度)int depth = 1 + max(leftdepth, rightdepth); // 中(左子树和右子树的根节点的高度, 包括根节点, 故+1)return depth;}int maxDepth(TreeNode* root) {return getdepth(root);}
};
迭代法(go ver)
/*** Definition for a binary tree node.* type TreeNode struct {* Val int* Left *TreeNode* Right *TreeNode* }*/
func maxDepth(root *TreeNode) int {// 使用迭代法的话,使用层序遍历是最为合适的,因为最大的深度就是二叉树的层数,和层序遍历的方式极其吻合queue := list.New()maxDepth := 0if root != nil {queue.PushBack(root)}for queue.Len() > 0 {// 记录当前队列长度size := queue.Len()for size > 0 {// 弹出并写入结果front := queue.Front()node := queue.Remove(front).(*TreeNode) // 存进list之后类型会变为*list.Element,要转换为*TreeNode// 左右节点入队列if node.Left != nil {queue.PushBack(node.Left)}if node.Right != nil {queue.PushBack(node.Right)}size -= 1}maxDepth += 1}return maxDepth
}
复杂度
时间复杂度:
空间复杂度:
思路总结
- 本题如果用迭代法,则直接使用层序遍历的模板解题即可
- 如果用递归法,则相对难一些:
- 首先要理解二叉树的深度和高度区别:
- 二叉树节点的深度:指从根节点到该节点的最长简单路径边的条数或者节点数(取决于深度从0开始还是从1开始)—— 即深度是从某节点角度往上(根节点)看的
- 二叉树节点的高度:指从该节点到叶子节点的最长简单路径边的条数或者节点数(取决于高度从0开始还是从1开始)—— 即高度是从某节点角度往下(叶子节点)看的
- 因此,根节点的高度就是二叉树的最大深度
- 本题可以使用前序(中左右),也可以使用后序遍历(左右中),使用前序求的就是深度,即最大的叶子节点深度,使用后序求的是高度,即根节点的高度。(后序遍历相对容易理解一些,见代码)
- 首先要理解二叉树的深度和高度区别:
相关文章:

力扣日记11.27-【二叉树篇】二叉树的最大深度
力扣日记:【二叉树篇】二叉树的最大深度 日期:2023.11.27 参考:代码随想录、力扣 104. 二叉树的最大深度 题目描述 难度: 给定一个二叉树 root ,返回其最大深度。 二叉树的 最大深度 是指从根节点到最远叶子节点的最…...
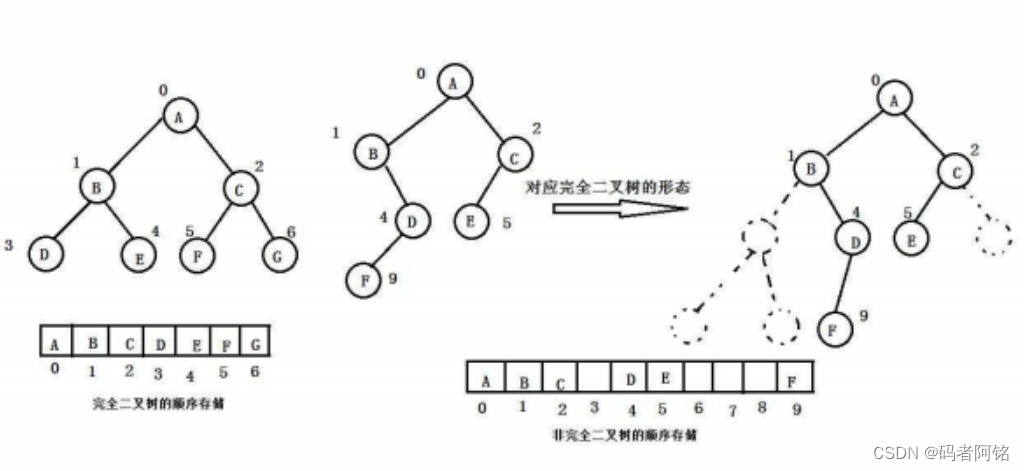
【数据结构】树的概念以及二叉树
目录 1 树概念及结构 1.1 树的概念 1.3 树的存储 2 二叉树的概念及结构 2.1 概念 2.2 特殊的二叉树 2.3 二叉树的性质 2.4 二叉树的存储结构 1 树概念及结构 1.1 树的概念 树是一种非线性的数据结构,它是由n(n>0)个有限结点组…...
软件测试职业规划导图
公司开发的产品专业性较强,软件测试人员需要有很强的专业知识,现在软件测试人员发展出现了一种测试管理者不愿意看到的景象: 1、开发技术较强的软件测试人员转向了软件开发(非测试工具开发); 2、业务能力较强的测试人员转向了软件…...
360压缩安装一半不动了?一分钟解决!
360压缩软件是我们常用的压缩软件,但是常常会遇到压缩安装到一半停止的情况,下面提供了一些可能的原因和解决办法,大家可以进行尝试~ 方法一:关闭防火墙和杀毒软件 有时候,防火墙和杀毒软件可能会阻止360压缩的安装过…...
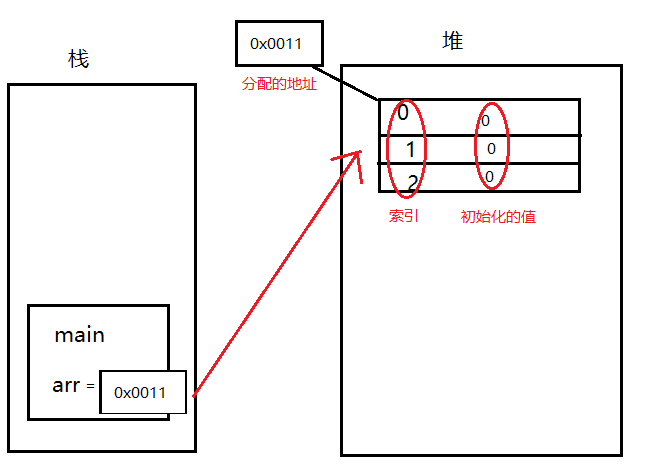
堆和栈的区别 重点来说一下堆和栈;堆与栈之间的联系
文章目录 堆和栈的区别重点来说一下堆和栈:那么堆和栈是怎么联系起来的呢? 堆与栈的区别 很明显: 今天来聊一聊java中的堆和栈,工作当中这两个也是经常遇到的,知识我们没有去注意理论上的这些内容,今天就来分享一下。…...

python 批量将图片存入excel单元格内
python 批量将图片存入excel单元格 示例代码1示例代码2 示例代码1 https://blog.csdn.net/wuyoudeyuer/article/details/128185284 # -*- coding: utf-8 -*- # Time : 2022-12-05 # Author : Carl_DJ 实现功能:在excel中,对应的名称后面,…...

Nginx常见的中间件漏洞
目录 1、Nginx文件名逻辑漏洞 2、Nginx解析漏洞 3、Nginx越权读取缓存漏洞 这里需要的漏洞环境可以看:Nginx 配置错误导致的漏洞-CSDN博客 1、Nginx文件名逻辑漏洞 该漏洞利用条件有两个: Nginx 0.8.41 ~ 1.4.3 / 1.5.0 ~ 1.5.7 php-fpm.conf中的s…...

Linux C语言 27-递归
Linux C语言 27-递归 本节关键字:C语言 递归 相关C库函数:main、printf 什么是递归? 在C语言中,程序调用自身的编程技巧称为递归(recursion)。递归从字面上可以理解为“递去归来”。 使用递归的优缺点 …...

redis运维(二十一)redis 的扩展应用 lua(三)
一 redis 的扩展应用 lua redis加载lua脚本文件 ① 调试lua脚本 redis-cli 通过管道 --pipe 快速导入数据到redis中 ② 预加载方式 1、错误方式 2、正确方式 "案例讲解" ③ 一次性加载 执行命令: redis-cli -a 密码 --eval Lua脚本路径 key …...

如何科学地划分医学图像数据集
在进行医学图像分类任务时,如何科学地划分数据集是一个重要的问题。这个问题的答案取决于你的数据特性和实验目标。一般来说,有两种常见的数据划分方法:按照比例划分和按照病例划分。 按照比例划分 按照比例划分是一种常见的方法,…...

【开源】基于Vue+SpringBoot的食品生产管理系统
项目编号: S 044 ,文末获取源码。 \color{red}{项目编号:S044,文末获取源码。} 项目编号:S044,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 加工厂管理模块2.2 客户管理模块2.3…...

如何减少40%的Docker构建时间
随着Docker的普及,许多公司的产品会将组件构建为Docker镜像。但随着时间的推移,一些镜像变得越来越大,对应的CI构建也变得越来越慢。 如果能在喝完一杯咖啡的时间(不超过5分钟)内完成构建,将是一个理想状态…...
Scrapy爬虫异步框架之持久化存储(一篇文章齐全)
1、Scrapy框架初识(点击前往查阅) 2、Scrapy框架持久化存储 3、Scrapy框架内置管道(点击前往查阅) 4、Scrapy框架中间件(点击前往查阅) Scrapy 是一个开源的、基于Python的爬虫框架,它提供了…...
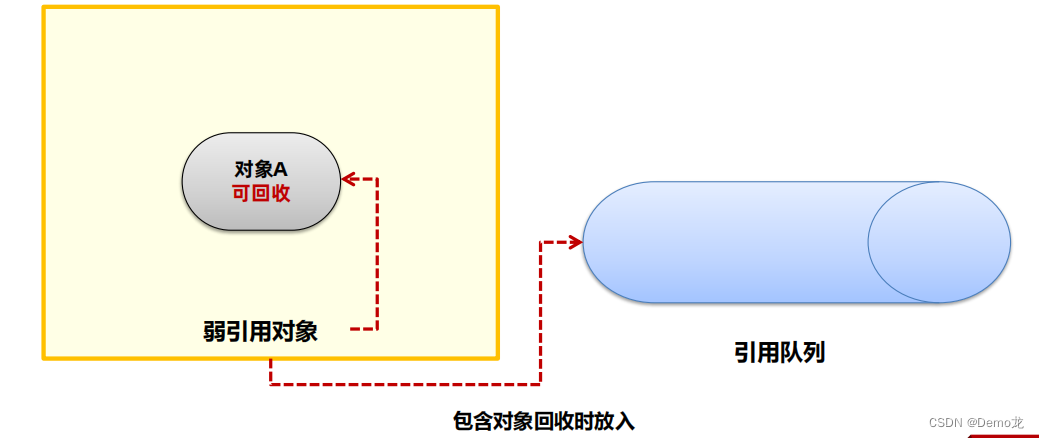
JVM——几种常见的对象引用
目录 1. 软引用软引用的使用场景-缓存 2.弱引用3.虚引用和终结器引用 可达性算法中描述的对象引用,一般指的是强引用,即是GCRoot对象对普通对象有引用关系,只要这层关系存在, 普通对象就不会被回收。除了强引用之外,Ja…...

C++期末考试选择题题库100道C++期末判断题的易错知识点复习
今天备考C,看到了一些好的复习资料,整合一起给大家分享一下 选择题 对于常数据成员,下面描述正确的是 【 B 】 A. 常数据成员必须被初始化,并且不能被修改 B. 常数据成员可以不初始化,并且不能被修改 C. 常数据成…...

使用qemu调试arm内核
参考书籍《奔跑吧Linux内核》–笨叔 下载Linux-5.0源码 https://benshushu.coding.net/public/runninglinuxkernel_5.0/runninglinuxkernel_5.0/git/files或者直接git源码 git clone https://e.coding.net/benshushu/runninglinuxkernel_5.0/runninglinuxkernel_5.0.git安装必…...

Pytorch深度学习实战2-1:详细推导Xavier参数初始化(附Python实现)
目录 1 参数初始化2 Xavier参数初始化原理2.1 前向传播阶段2.2 反向传播阶段2.3 可视化思考 3 Python实现 1 参数初始化 参数初始化在深度学习中起着重要的作用。在神经网络中,参数初始化是指为模型中的权重和偏置项设置初始值的过程。合适的参数初始化可以帮助模型…...

Java的threadd常用方法
常用API 给当前线程命名 主线程 package com.itheima.d2;public class ThreadTest1 {public static void main(String[] args) {Thread t1 new MyThread("子线程1");//t1.setName("子线程1");t1.start();System.out.println(t1.getName());//获得子线程…...
一键修复0xc000007b错误代码,科普关于0xc000007b错误的原因
最近很多用户都有遇到过0xc000007b错误的问题,出现这样的问题想必大家都会手足无措吧,其实解决这样的问题也有很简单的解决方法,这篇文章就来教大家如何一键修复0xc000007b,同时给大家科普一下关于0xc000007b错误的原因࿰…...
使用Selenium、Python和图鉴打码平台实现B站登录
selenium实战之模拟登录b站 基础知识铺垫: 利用selenium进行截图: driver.save_screenshot() 注意图片文件名要用png结尾. 关于移动: ActionChains(bro).move_to_element_with_offset()# 对于某个图像ActionChains(bro).move_by_offset(…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...
