【机器学习】On the Identifiability of Nonlinear ICA: Sparsity and Beyond
前言
本文是对On the Identifiability of Nonlinear ICA: Sparsity and Beyond (NIPS 2022)中两个结构稀疏假设的总结。原文链接在Reference中。
什么是ICA(Independent component analysis)?
独立成分分析简单来说,就是给定很多的样本X,通过样本分离出组合成样本的源S。
关于ICA的详细内容,可以参考Yifan Shen的博客:ICA简明攻略
非线性独立成分分析
非线性独立成分分析(ICA)旨在从其可观测的非线性混合物中恢复潜在的独立源。非线性独立成分分析(ICA)是无监督学习的基础。它推广了线性ICA(Comon, 1994),用于从观测数据中识别潜在源。这些观测数据是源的非线性混合。对于观测向量 x x x,非线性ICA将其表示为 x = f ( s ) x = f(s) x=f(s), f f f是一个未知的可逆混合函数, s s s是表示(边缘上)独立源的潜在随机向量。非线性ICA问题的困难点在于,在没有额外假设的情况下是不可解的。即在没有额外假设或限制的情况下,把观测变量分解为独立的元素存在无穷种解。同时分离后的元素仍然是源的混合。
现有的研究引入了辅助变量 u u u(例如,类别标签、域索引、时间索引),并假设在给定 u u u的条件下源是条件独立的。关于这部分工作如果感兴趣可以去看 Hyvärinen的talk。
条件独立
P ( A , B ∣ C ) = P ( A ∣ C ) ⋅ P ( B ∣ C ) P(A, B|C) = P(A|C) \cdot P(B|C) P(A,B∣C)=P(A∣C)⋅P(B∣C)
一个很好的例子:
C指赖床,A指熬夜,B指迟到, P ( A , B ∣ C ) = P ( A ∣ C ) ⋅ P ( B ∣ C ) P(A, B|C) = P(A|C) \cdot P(B|C) P(A,B∣C)=P(A∣C)⋅P(B∣C),赖床的发生使得熬夜想通过赖床来影响迟到的可能为零,即没有别的可能来影响迟到了,所以此时熬夜和迟到就是条件独立了。
结构稀疏(Structural Sparsity)假设
Theorem 1. Let the observed data be sampled from a nonlinear ICA model as defined in Eqs. (1) and (2). Suppose the following assumptions hold:
i. Mixing function f f f is invertible and smooth. Its inverse is also smooth.
ii. For all i ∈ { 1 , … , n } i \in \{1, \ldots, n\} i∈{1,…,n} and j ∈ F i , : j \in \mathcal{F}_{i, :} j∈Fi,:, there exist { s ( ℓ ) } ℓ = 1 ∣ F i , : ∣ \{s^{(\ell)}\}_{\ell=1}^{|\mathcal{F}_{i, :}|} {s(ℓ)}ℓ=1∣Fi,:∣ and T T T s.t. span { J f ( s ( ℓ ) ) i , : } ℓ = 1 ∣ F i , : ∣ = R F i , : n \text{span}\{J_f(s^{(\ell)})_{i, :}\}_{\ell=1}^{|\mathcal{F}_{i, :}|} = \mathbb{R}^n_{\mathcal{F}_{i, :}} span{Jf(s(ℓ))i,:}ℓ=1∣Fi,:∣=RFi,:n and [ J f ( s ( ℓ ) ) T ] j , : ∈ R F ^ i , : n [J_f(s^{(\ell)})^T]_{j, :} \in \mathbb{R}^{n}_{\hat{\mathcal{F}}_{i, :}} [Jf(s(ℓ))T]j,:∈RF^i,:n.
iii. ∣ F ^ ∣ ≤ ∣ F ∣ |\hat{\mathcal{F}}| \leq |\mathcal{F}| ∣F^∣≤∣F∣.
iv. (Structural Sparsity) For all k ∈ { 1 , … , n } k \in \{1, \ldots, n\} k∈{1,…,n}, there exists C k C_k Ck such that
⋂ i ∈ C k F i , : = { k } . \bigcap_{i \in C_k} \mathcal{F}_{i, :} = \{k\}. i∈Ck⋂Fi,:={k}.
Then h : = f ^ − 1 ∘ f h := \hat{f}^{-1} \circ f h:=f^−1∘f is a composition of a component-wise invertible transformation and a permutation.
![![[Pasted image 20231121180751.png]]](https://img-blog.csdnimg.cn/d3b52fc548474c16b87d835e92872473.png)
符号含义
- J f ( s ) {J_f(s)} Jf(s)表示对源矩阵求偏导得到的雅可比矩阵,如上图所示。
- KaTeX parse error: Got function '\hat' with no arguments as subscript at position 4: {J_\̲h̲a̲t̲{f}(\hat{s})} 表示源矩阵经过变换后得到的矩阵求偏导得到的雅可比矩阵。其实就是表示nonlinear ICA求解后得到的矩阵求偏导。因为在有解的情况下,求解出的源只是真实源的排列组合,因此表示称这种形式。后面会用预测值来表示带hat的量。
- F \mathcal{F} F 表示雅各比矩阵 J f ( s ) {J_f(s)} Jf(s)的support,也就是其不为0的点组成的集合。
- F ^ \hat{\mathcal{F}} F^ 表示雅各比矩阵KaTeX parse error: Got function '\hat' with no arguments as subscript at position 4: {J_\̲h̲a̲t̲{f}(\hat{s})}的support,也就是其不为0的点组成的集合。
- i , : i,: i,: 表示的是某一行中所有不为0点的索引。也就是横坐标固定,列坐标任取。
- s ( l ) s^{(l)} s(l)表示的是第l个源
- C k C_k Ck
理论拆解:
- 第一条很容易理解。由观测样本X恢复出源S的过程是一个求逆的过程。在 f f f是可逆平滑的情况下才可以求逆,求导。
- 第二条表示的意思是源S可能的组合空间足够大(实数)。这条是为了避免ill-posed conditions。比如雅可比矩阵的某一个部分一直满足后面的假设条件,使得假设虽然成立但仍无法求解。
- 第三条表示预测雅可比矩阵support的数量小于等于真实雅可比矩阵support support的数量。
- 第四条表示的意思是,对于某一列 C k C_k Ck中的行 i i i来说,从support集合 F \mathcal{F} F中取行坐标为 i i i的所有坐标点,也就是取了某一行上的所有support。依次取出所有行的support,在列方向上求交集。一定存在这样的列,它的列坐标是k,可以保证这列存在不止一个support(存在交集),同时这列存在这些support的对应行只在这列上有交集(意思是某些观测值的共同源只有一个)。概括来说就是,一定至少存在一个源,是某些观测变量的唯一共同源。
满足上述条件的情况下,可以得到对源 s s s做变换 f f f得到实际的 x = f ( s ) x=f(s) x=f(s),再做逆变换 f − 1 f^{-1} f−1
整个过程是分量逐一逆变换加上排列,也就是component-wise invertible transformation and a permutation。
证明
问题简化
证明的目标是 h : = f ^ − 1 ∘ f h := \hat{f}^{-1} \circ f h:=f^−1∘f 为源s的permutation with component-wise invertible变换。也就是: f ^ = f ∘ h − 1 ( s ) \hat{f} = f \circ h^{-1}(s) f^=f∘h−1(s). 假设 D ( s ) D(s) D(s) 表示一个对角矩阵, P P P 表示一个排列变换矩阵。通过使用链式法则, 我们可以把 f ^ = f ∘ h − 1 ( s ) \hat{f} = f \circ h^{-1}(s) f^=f∘h−1(s) 表示为:
J f ^ ( s ^ ) = J f ∘ h − 1 ( h ( s ) ) = J f ∘ g − 1 ∘ P − 1 ( P g ( s ) ) = J f ∘ g − 1 ( P − 1 P g ( s ) ) J P − 1 ( P g ( s ) ) = J f ∘ g − 1 ( g ( s ) ) J P − 1 ( P g ( s ) ) = J f ( g − 1 ( g ( s ) ) ) J g − 1 ( g ( s ) ) J P − 1 ( P g ( s ) ) = J f ( s ) D ( s ) P , (1) \begin{aligned} J_{\hat{f}}(\hat{s}) &= J_{f \circ h^{-1}}(h(s)) \\ &= J_{f \circ g^{-1} \circ P^{-1}}(Pg(s)) \\ &= J_{f \circ g^{-1}}(P^{-1}Pg(s)) J_{P^{-1}}(Pg(s)) \\ &= J_{f \circ g^{-1}}(g(s)) J_{P^{-1}}(Pg(s)) \\ &= J_{f}(g^{-1}(g(s))) J_{g^{-1}}(g(s)) J_{P^{-1}}(Pg(s)) \\ &= J_{f}(s)D(s)P, \end{aligned} \tag{1} Jf^(s^)=Jf∘h−1(h(s))=Jf∘g−1∘P−1(Pg(s))=Jf∘g−1(P−1Pg(s))JP−1(Pg(s))=Jf∘g−1(g(s))JP−1(Pg(s))=Jf(g−1(g(s)))Jg−1(g(s))JP−1(Pg(s))=Jf(s)D(s)P,(1)
其中,g是一个元素可逆函数(invertible element-wise function)。
接着用 T ( s ) = D ( s ) P T(s) = D(s)P T(s)=D(s)P 来表示 D ( s ) P D(s)P D(s)P , T ( s ) T(s) T(s)是可逆的。由此目标可以转化为证明(2)成立:
J f ^ ( s ^ ) = J f ( s ) T ( s ) , (2) J_{\hat{f}}(\hat{s}) = J_{f}(s)T(s), \tag{2} Jf^(s^)=Jf(s)T(s),(2)
也就是我们希望证明预测得到的雅可比矩阵,只是真实雅可比矩阵的一个排列。
如果变换 T ( s ) T(s) T(s)不是一个简单的排列变换,也就是 T ( s ) ≠ D ( s ) P T(s) \neq D(s)P T(s)=D(s)P,那么(2)就不成立。如果我们能证明 T ( s ) = D ( s ) P T(s) = D(s)P T(s)=D(s)P,也就能说明(2)成立。
接着我们的目标就转化为证明:
T ( s ) = D ( s ) P , (3) T(s) = D(s)P, \tag{3} T(s)=D(s)P,(3)
找源雅可比矩阵,预测雅可比矩阵,变换矩阵T之间的关系
用 F \mathcal{F} F 表示 J f ( s ) J_f(s) Jf(s) 的支撑集, F ^ \hat{\mathcal{F}} F^ 表示 J f ^ ( s ^ ) J_{\hat{f}}(\hat{s}) Jf^(s^) 的支撑集, τ \tau τ 表示 T ( s ) T(s) T(s) 的支撑集, T T T 表示具有支撑集 τ \tau τ 的矩阵。根据假设 ii,我们可以得到:
span { J f ( s ( ℓ ) ) i } ℓ = 1 ∣ F i , : ∣ = R F i , : n (4) \text{span}\{J_f(s^{(\ell)})_i\}_{\ell=1}^{|\mathcal{F}_{i, :}|} = \mathbb{R}^n_{\mathcal{F}_{i, :}} \tag{4} span{Jf(s(ℓ))i}ℓ=1∣Fi,:∣=RFi,:n(4)
由于 { J f ( s ( ℓ ) ) i } ℓ = 1 ∣ F i , : ∣ \{J_f(s^{(\ell)})_i\}_{\ell=1}^{|\mathcal{F}_{i, :}|} {Jf(s(ℓ))i}ℓ=1∣Fi,:∣ 形成了 R F i , : n \mathbb{R}^n_{\mathcal{F}_{i, :}} RFi,:n 的一组基,对于任意 j 0 ∈ F i , : j_0 \in \mathcal{F}_{i, :} j0∈Fi,:,我们可以将热独向量 e j 0 ∈ R F i , : n e_{j_0} \in \mathbb{R}^n_{\mathcal{F}_{i, :}} ej0∈RFi,:n 重写为:
e j 0 = ∑ ℓ ∈ F i , : α ℓ J f ( s ( ℓ ) ) i , : , (5) e_{j_0} = \sum_{\ell \in \mathcal{F}_{i, :}} \alpha_{\ell} J_f(s^{(\ell)})_{i, :}, \tag{5} ej0=ℓ∈Fi,:∑αℓJf(s(ℓ))i,:,(5)
其中 α ℓ \alpha_{\ell} αℓ 是对应的系数。则有:
T j 0 , : = e j 0 T = ∑ ℓ ∈ F i , : α ℓ J f ( s ( ℓ ) ) i , : ⋅ T ∈ R F ^ i , : n , (6) T_{j_0, :} = e_{j_0} T = \sum_{\ell \in \mathcal{F}_{i, :}} \alpha_{\ell} J_f(s^{(\ell)})_{i, :} \cdot T \in \mathbb{R}^n_{\hat{\mathcal{F}}_{i, :}}, \tag{6} Tj0,:=ej0T=ℓ∈Fi,:∑αℓJf(s(ℓ))i,:⋅T∈RF^i,:n,(6)
公式(6)的“ ∈ \in ∈”符号来自于假设 ii,即(6)求和中的每个元素都属于 R F ^ i , : n \mathbb{R}^n_{\hat{\mathcal{F}}_{i, :}} RF^i,:n。因此有:
∀ j ∈ F i , : , T j , : ∈ R F ^ i , : n (7) \forall j \in \mathcal{F}_{i, :}, \quad T_{j, :} \in \mathbb{R}^n_{\hat{\mathcal{F}}_{i, :}} \tag{7} ∀j∈Fi,:,Tj,:∈RF^i,:n(7)
到这一步我们推出了 T j , : T_{j, :} Tj,: 是属于预测矩阵的支撑集的。
然后我们可以在支撑集之间建立如下关系:
∀ ( i , j ) ∈ F , { i } × τ j , : ⊆ F ^ . (8) \forall (i, j) \in \mathcal{F}, \{i\} \times \tau_{j, :} \subseteq \hat{\mathcal{F}}. \tag{8} ∀(i,j)∈F,{i}×τj,:⊆F^.(8)
需要注意,这里的 × \times ×表示的是combine。意思是横坐标 i {i} i和 τ j , : \tau_{j, :} τj,:表示的纵坐标组合起来。
根据假设 i, T ( s ) T(s) T(s) 是一个可逆矩阵,这意味着它有一个非零的行列式值。将矩阵 T ( s ) T(s) T(s) 的行列式为它的 Leibniz 公式展开:
det ( T ( s ) ) = ∑ σ ∈ S n { sgn ( σ ) ∏ i = 1 n T ( s ) i , σ ( i ) } ≠ 0. (9) \text{det}(T(s)) = \sum_{\sigma \in S_n} \{\text{sgn}(\sigma) \prod_{i=1}^n T(s)_{i,\sigma(i)}\} \neq 0. \tag{9} det(T(s))=σ∈Sn∑{sgn(σ)i=1∏nT(s)i,σ(i)}=0.(9)
其中 S n S_n Sn 是 n n n排列的集合。
由于(9)不为0, 则存在至少一个求和元素是非零的,表示为:
∃ σ ∈ S n , ∀ i ∈ { 1 , … , n } , sgn ( σ ) ∏ i = 1 n T ( s ) i , σ ( i ) ≠ 0. (10) \exists \sigma \in S_n, \forall i \in \{1, \ldots, n\}, \text{sgn}(\sigma) \prod_{i=1}^n T(s)_{i,\sigma(i)} \neq 0. \tag{10} ∃σ∈Sn,∀i∈{1,…,n},sgn(σ)i=1∏nT(s)i,σ(i)=0.(10)
(10)等价于:
∃ σ ∈ S n , ∀ i ∈ { 1 , … , n } , T ( s ) i , σ ( i ) ≠ 0. (11) \exists \sigma \in S_n, \forall i \in \{1, \ldots, n\}, T(s)_{i,\sigma(i)} \neq 0. \tag{11} ∃σ∈Sn,∀i∈{1,…,n},T(s)i,σ(i)=0.(11)
由此我们可以得到 σ ( ⋅ ) \sigma(·) σ(⋅) 在 T ( s ) T(s) T(s) 的支持集中,进而有:
∀ j ∈ { 1 , … , n } , σ ( j ) ∈ T j , : (12) \forall j \in \{1, \ldots, n\}, \sigma(j) \in T_{j, :} \tag{12} ∀j∈{1,…,n},σ(j)∈Tj,:(12)
结合 (8),可以得到:
∀ ( i , j ) ∈ F , ( i , σ ( j ) ) ∈ { i } × T j , : ⊆ F ^ . (13) \forall (i, j) \in \mathcal{F}, (i, \sigma(j)) \in \{i\} \times T_{j, :} \subseteq \hat{\mathcal{F}}. \tag{13} ∀(i,j)∈F,(i,σ(j))∈{i}×Tj,:⊆F^.(13)
表示
σ ( F ) = { ( i , σ ( j ) ) ∣ ( i , j ) ∈ F } . (14) \sigma(\mathcal{F}) = \{(i, \sigma(j)) | (i, j) \in \mathcal{F}\}. \tag{14} σ(F)={(i,σ(j))∣(i,j)∈F}.(14)
以上我们得到了 F \mathcal{F} F, F ^ \hat{\mathcal{F}} F^, T T T 之间的变换关系。
反证法证明 T ( s ) = D ( s ) P T(s) = D(s)P T(s)=D(s)P成立
假设 T ( s ) ≠ D ( s ) P T(s) \neq D(s)P T(s)=D(s)P,那么:
∃ j 1 ≠ j 2 , τ j 1 , : ∩ τ j 2 , : ≠ ∅ . (15) \exists j_1 \neq j_2, \tau_{j_1, :} \cap \tau_{j_2, :} \neq \varnothing. \tag{15} ∃j1=j2,τj1,:∩τj2,:=∅.(15)
此外,考虑 j 3 ∈ { 1 , … , n } j_3 \in \{1, \ldots, n\} j3∈{1,…,n} 使得:
σ ( j 3 ) ∈ τ j 1 , : ∩ τ j 2 , : . (16) \sigma(j_3) \in \tau_{j_1, :} \cap \tau_{j_2, :}. \tag{16} σ(j3)∈τj1,:∩τj2,:.(16)
因为 j 1 ≠ j 2 j_1 \neq j_2 j1=j2,我们可以假设 j 3 ≠ j 1 j_3 \neq j_1 j3=j1 而不失一般性(矩阵通常很大, j 3 = j 1 j_3 = j_1 j3=j1 只是概率非常非常小的一种情况,概率小到 1 n \frac{1}{n} n1)。
根据假设 iv, 存在 j 1 ∈ C j 1 j_1 \in C_{j_1} j1∈Cj1 使得:
⋂ i ∈ C j 1 F i , : = { j 1 } . (17) \bigcap_{i \in C_{j_1}} \mathcal{F}_{i, :} = \{j_1\}. \tag{17} i∈Cj1⋂Fi,:={j1}.(17)
由于:
j 3 ∉ { j 1 } = ⋂ i ∈ C j 1 F i , : , (18) j_3 \not\in \{j_1\} = \bigcap_{i \in C_{j_1}} \mathcal{F}_{i, :}, \tag{18} j3∈{j1}=i∈Cj1⋂Fi,:,(18)
那么一定存在 i 3 ∈ C j 1 i_3 \in C_{j_1} i3∈Cj1 使得:
j 3 ∉ F i 3 , : (19) j_3 \not\in \mathcal{F}_{i_3, :} \tag{19} j3∈Fi3,:(19)
因为 j 1 ∈ F i 3 , : j_1 \in \mathcal{F}_{i_3, :} j1∈Fi3,:,我们有 ( i 3 , j 1 ) ∈ F (i_3, j_1) \in \mathcal{F} (i3,j1)∈F。然后根据公式 (8),可以得到:
{ i 3 } × τ j 1 , : ⊆ F ^ . (20) \{i_3\} \times \tau_{j_1, :} \subseteq \hat{\mathcal{F}}. \tag{20} {i3}×τj1,:⊆F^.(20)
由 σ ( j 3 ) ∈ τ j 1 , : ∩ τ j 2 , : \sigma(j_3) \in \tau_{j_1, :} \cap \tau_{j_2, :} σ(j3)∈τj1,:∩τj2,: 可以得到:
( i 3 , σ ( j 3 ) ) ∈ { i 3 } × τ j 1 , : . (21) (i_3, \sigma(j_3)) \in \{i_3\} \times \tau_{j_1, :}. \tag{21} (i3,σ(j3))∈{i3}×τj1,:.(21)
通过公式(20) 和 (21),我们可以得到:
( i 3 , σ ( j 3 ) ) ∈ F ^ , (22) (i_3, \sigma(j_3)) \in \hat{\mathcal{F}}, \tag{22} (i3,σ(j3))∈F^,(22)
结合公式 (14) 可知 ( i 3 , j 3 ) ∈ F (i_3, j_3) \in \mathcal{F} (i3,j3)∈F,与等式 (19) 矛盾。
则可知假设 T ( s ) ≠ D ( s ) P T(s) \neq D(s)P T(s)=D(s)P不成立。
则 T ( s ) = D ( s ) P T(s) = D(s)P T(s)=D(s)P,得证。
不完备情况下的结构稀疏假设
不完备指观测样本的数量远大于源的数量
Theorem 2. Let the observed data be sampled from a linear ICA model defined in Eqs. ( 1 ) (1) (1) and ( 3 ) (3) (3) with Gaussian sources. Differently, the number of observed variables (denoted as m m m) could be larger than that of the sources n n n, i.e., m ≥ n m \geq n m≥n. Suppose the following assumptions hold:
i. The nonzero coefficients of the mixing matrix A \mathbf{A} A are randomly drawn from a distribution that is absolutely continuous with respect to Lebesgue measure.
ii. The estimated mixing matrix A ^ \hat{A} A^ has the minimal L 0 L_0 L0 norm during estimation.
iii. (Structural Sparsity) Given C ⊆ { 1 , 2 , … , n } C \subseteq \{1,2,\ldots,n\} C⊆{1,2,…,n} where ∣ C ∣ > 1 |C| > 1 ∣C∣>1, let A C ∈ R m × ∣ C ∣ A_C \in \mathbb{R}^{m \times |C|} AC∈Rm×∣C∣ represents a submatrix of A ∈ R m × n A \in \mathbb{R}^{m \times n} A∈Rm×n consisting of columns with indices C C C. Then, for all k ∈ C k \in C k∈C, we have
∣ ⋃ k ′ ∈ C supp ( A k ′ ) ∣ − rank ( overlap ( A C ) ) > ∣ supp ( A k ) ∣ . \left| \bigcup_{k' \in C} \text{supp}(A_{k'}) \right| - \text{rank}(\text{overlap}(A_C)) > \left| \text{supp}(A_k) \right|. k′∈C⋃supp(Ak′) −rank(overlap(AC))>∣supp(Ak)∣.
Then A ^ = A D P \hat{A} = ADP A^=ADP with probability one, where D D D is a diagonal matrix and P P P is a column permutation matrix.
![![[Pasted image 20231122193737.png]]](https://img-blog.csdnimg.cn/746dbb14ffbd41efb46205a0db300725.png)
理论拆解:
- 第一条:保证了混合矩阵的结构足够复杂,不是特殊的单一结构。
- 第二条:L0正则化表示的是矩阵中不为0的点的数量。这条表示预测的混合矩阵越稀疏越好。
- 第三条:support的并集(按行求并,也就是向行投影)中support的数量 - 行重叠子矩阵的秩 > 每一列的support support数量。假设的目的是:每个source影响的观测越少越好,source共同作用越小越好。图中是一个例子, k = 1 k = 1 k=1 并且 C = { 1 , 2 , 3 } C = \{1,2,3\} C={1,2,3}。让 A C A_C AC 表示图中所示的子矩阵,其中 ∣ ⋃ k ′ ∈ C supp ( A k ′ ) ∣ = 7. \left| \bigcup_{k' \in C} \text{supp}(A_{k'}) \right| = 7. ⋃k′∈Csupp(Ak′) =7.蓝色虚线方块表示 overlap ( A C ) \text{overlap}(A_C) overlap(AC) , rank ( overlap ( A C ) ) = 2 \text{rank}(\text{overlap}(A_C)) = 2 rank(overlap(AC))=2。因此, ∣ ⋃ k ′ ∈ C supp ( A k ′ ) ∣ − rank ( overlap ( A C ) ) = 5 (黑点的数量) , \left| \bigcup_{k' \in C} \text{supp}(A_{k'}) \right| - \text{rank}(\text{overlap}(A_C)) = 5 \text{(黑点的数量)}, ⋃k′∈Csupp(Ak′) −rank(overlap(AC))=5(黑点的数量),比 ∣ supp ( A 1 ) ∣ = 4 \left| \text{supp}(A_1) \right| = 4 ∣supp(A1)∣=4 大。
证明
根据假设(ii),我们考虑以下组合优化问题:
U ^ : = arg min U ∈ R s × s , U U T = I s ∥ A U ∥ 0 , (1) \hat{U} := \arg \min_{U \in \mathbb{R}^{s \times s}, UU^T=I_s} \|AU\|_0,\tag{1} U^:=argU∈Rs×s,UUT=Ismin∥AU∥0,(1)
其中 A A A 是真实的混合矩阵, U ^ \hat{U} U^ 表示对应于优化问题解的旋转矩阵。设 A ^ = A U ^ \hat{A} = A\hat{U} A^=AU^。
用反证法,假设 A ^ ≠ A D P \hat{A} \neq ADP A^=ADP,那么 U ^ ≠ D P \hat{U} \neq DP U^=DP。
这意味着存在某个 j ′ ∈ { 1 , … , s } j' \in \{1, \ldots, s\} j′∈{1,…,s} 和它对应的行索引集合 I j ′ \mathcal{I}_{j'} Ij′ ( ∣ I j ′ ∣ > 1 |\mathcal{I}_{j'}| > 1 ∣Ij′∣>1),使得 U ^ i , j ′ ≠ 0 \hat{U}_{i,j'} \neq 0 U^i,j′=0 对所有 i ∈ I j ′ i \in \mathcal{I}_{j'} i∈Ij′成立,并且 U ^ i , j ′ = 0 \hat{U}_{i,j'} = 0 U^i,j′=0 对所有 i ∉ I j ′ i \notin \mathcal{I}_{j'} i∈/Ij′成立。
由于 U ^ \hat{U} U^ 是可逆的并且具有完整的行秩,为了避免列之间的线性依赖,存在唯一对应于 j ′ j' j′ 的行索引 i ′ i' i′。设:
U ^ : = [ U ^ 1 … U ^ s ] , \hat{U} := \begin{bmatrix} \hat{U}_1 & \ldots & \hat{U}_s \end{bmatrix}, U^:=[U^1…U^s],
我们可以得到:
∥ A ^ j ′ ∥ 0 = ∥ A U ^ j ′ ∥ 0 = ∥ ∑ i ∈ I j ′ A i U ^ i , j ′ ∥ 0 . (2) \|\hat{A}_{j'}\|_0 = \|A\hat{U}_{j'}\|_0 = \left\| \sum_{i \in \mathcal{I}_{j'}} A_{i} \hat{U}_{i,j'} \right\|_0. \tag{2} ∥A^j′∥0=∥AU^j′∥0= i∈Ij′∑AiU^i,j′ 0.(2)
这里的 ∥ ⋅ ∥ 0 \|\cdot\|_0 ∥⋅∥0 表示 L 0 L_0 L0 范数,即矩阵中非零元素的数量。
设 A I j A_{\mathcal{I}_j} AIj 表示由 A A A 的列索引 I j \mathcal{I}_j Ij 组成的子矩阵。注意 A i A_i Ai 表示矩阵 A A A 的第 i i i 列。根据假设 (ii, iii),由于 ∣ I j ′ ∣ > 1 |\mathcal{I}_{j'}| > 1 ∣Ij′∣>1 并且 U i , j ′ ≠ 0 U_{i,j'} \neq 0 Ui,j′=0,我们有:
∥ ∑ i ∈ I j ′ A i U ^ i , j ′ ∥ 0 ≥ ∣ ⋃ i ∈ I j ′ supp ( A i ) ∣ − rank ( overlap ( A I j ′ ) ) > ∣ supp ( A i ′ ) ∣ , (3) \left\|\sum_{i \in \mathcal{I}_{j'}} A_i \hat{U}_{i,j'}\right\|_0 \geq \left| \bigcup_{i \in \mathcal{I}_{j'}}\text{supp}(A_{i}) \right| - \text{rank}(\text{overlap}(A_{\mathcal{I}_{j'}})) > \left| \text{supp}(A_{i'}) \right|,\tag{3} i∈Ij′∑AiU^i,j′ 0≥ i∈Ij′⋃supp(Ai) −rank(overlap(AIj′))>∣supp(Ai′)∣,(3)
其中,项 rank ( overlap ( A I j ′ ) ) \text{rank}(\text{overlap}(A_{\mathcal{I}_{j'}})) rank(overlap(AIj′)) 表示其所有非零项可能被矩阵的线性组合 ∑ i ∈ I j ′ , A i \sum_{i \in \mathcal{I}_{j'}, A_i} ∑i∈Ij′,Ai 消除的行的最大数量。假设 i 排除了违反上述公式的情况,例如, A A A 的两列具有相同的值和support。进而可以保证:
∥ ∑ i ∈ I j ′ A i U ^ i , j ′ ∥ 0 > ∣ supp ( A i ′ ) ∣ = ∥ A i ′ ∥ 0 = ∥ A i ′ U ^ i ′ , j ′ ∥ 0 . (4) \left\|\sum_{i \in \mathcal{I}_{j'}} A_i \hat{U}_{i,j'}\right\|_0 > \left| \text{supp}(A_{i'}) \right| = \left\|A_{i'}\right\|_0 = \left\| A_{i'} \hat{U}_{i',j'} \right\|_0.\tag{4} i∈Ij′∑AiU^i,j′ 0>∣supp(Ai′)∣=∥Ai′∥0= Ai′U^i′,j′ 0.(4)
然后我们可以构造 U ~ : = [ U ~ 1 … U ~ s ] \tilde{U} := \begin{bmatrix} \tilde{U}_1 & \ldots & \tilde{U}_s \end{bmatrix} U~:=[U~1…U~s]。
首先,我们将 U ~ i , j ′ \tilde{U}_{i,j'} U~i,j′ 设置为列 U ~ j ′ \tilde{U}_{j'} U~j′ 中的唯一非零项。为了简便起见,我们可以将 U ~ i , j ′ \tilde{U}_{i,j'} U~i,j′ 设为 1。对于其他 j ≠ j ′ j \neq j' j=j′ 并且 U ^ i , j ≠ 0 \hat{U}_{i,j} \neq 0 U^i,j=0的列 U ~ j \tilde{U}_{j} U~j,我们设 U ~ i , j = 1 \tilde{U}_{i,j} = 1 U~i,j=1。因此:
∥ A U j ^ ∥ 0 > ∥ A U ~ j ∥ 0 , j = j ′ , ∥ A U ^ j ∥ 0 = ∥ A U ~ j ∥ 0 , j ≠ j ′ . (5) \begin{align} \left\|A\hat{U_{j}}\right\|_0 &> \left\|A\tilde{U}_{j}\right\|_0, & j = j', \\ \left\|A\hat{U}_{j}\right\|_0 &= \left\|A\tilde{U}_{j}\right\|_0, & j \neq j'. \end{align} \tag{5} AUj^ 0 AU^j 0> AU~j 0,= AU~j 0,j=j′,j=j′.(5)
由于假设 iii 涵盖了所有列,公式 (4) 对于任何 j ′ ∈ { 1 , … , s } j' \in \{1, \ldots, s\} j′∈{1,…,s} 都成立。如果存在多个 U ^ \hat{U} U^ 的列有多于一个非零项,为每一个列计算得到公式(4)。将不同的目标列索引 j ′ j' j′ 的集合表示为 J J J。对于 j ∈ J j \in J j∈J,设 U ^ i , j = 1 \hat{U}_{i,j} = 1 U^i,j=1,其中 i j i_j ij 是列 U j U_{j} Uj 中对应的非零项的唯一索引。对于其他 j ∉ J j \not\in J j∈J 并且 U i , j ≠ 0 U_{i,j} \neq 0 Ui,j=0的列 U j U_{j} Uj,设 U i , j = 1 U_{i,j} = 1 Ui,j=1。则有:
{ ∥ A U ^ j ∥ 0 > ∥ A U ~ j ∥ 0 , j ∈ J , ∥ A U ^ j ∥ 0 = ∥ A U ~ j ∥ 0 , j ∉ J . \left\{ \begin{aligned} \|A{\hat{U}_j}\|_0 &> \|A{\tilde{U}_j}\|_0, & j \in J, \\ \|A{\hat{U}_j}\|_0 &= \|A{\tilde{U}_j}\|_0, & j \notin J. \end{aligned} \right. {∥AU^j∥0∥AU^j∥0>∥AU~j∥0,=∥AU~j∥0,j∈J,j∈/J.
如前所述,每个列索引 j j j 对应一个唯一的行索引。 U ~ \tilde{U} U~ 是一个置换矩阵且 U ~ U ~ T = I s \tilde{U}\tilde{U}^T = I_s U~U~T=Is。因此有:
∥ A U ^ ∥ 0 > ∥ A U ~ ∥ 0 , (7) \left\|A\hat{U}\right\|_0 > \left\|A\tilde{U}\right\|_0,\tag{7} AU^ 0> AU~ 0,(7)
根据(1), U ^ \hat{U} U^应该是最小值,而(7)说明当 U ^ ≠ D P \hat{U} \neq DP U^=DP时, U ^ \hat{U} U^ 不是最小值。与定义相违背。因此证明 U ^ = D P \hat{U} = DP U^=DP,也就是 A ^ = A D P \hat{A} = ADP A^=ADP成立。
Reference
- Zheng, Yujia, Ignavier Ng, and Kun Zhang. “On the identifiability of nonlinear ica: Sparsity and beyond.” Advances in Neural Information Processing Systems 35 (2022): 16411-16422.
相关文章:
【机器学习】On the Identifiability of Nonlinear ICA: Sparsity and Beyond
前言 本文是对On the Identifiability of Nonlinear ICA: Sparsity and Beyond (NIPS 2022)中两个结构稀疏假设的总结。原文链接在Reference中。 什么是ICA(Independent component analysis)? 独立成分分析简单来说,就是给定很多的样本X,通…...
)
RBAC(Role-Based Access Control,基于角色的访问控制)
1. RBAC核心概念 RBAC(Role-Based Access Control,基于角色的访问控制)是一种广泛应用于软件和系统中的权限管理模型。它通过将用户与角色关联,再将角色与访问权限关联,来管理用户对系统资源的访问。RBAC模型的主要特…...

C++const指针的两种用法
const int *p &a; 指向const变量的指针 指向const变量的指针const修饰的变量,只能由指向const变量的指针去指向 p &a1;const的位置,必须在*的左边指向const变量的指针,可以被改变,可以指向别的变量可以指向普通变量&am…...

【Proteus仿真】【51单片机】智能垃圾桶设计
文章目录 一、功能简介二、软件设计三、实验现象联系作者 一、功能简介 本项目使用Proteus8仿真51单片机控制器,使用报警模块、LCD1602液晶模块、按键模块、人体红外传感器、HCSR04超声波、有害气体传感器、SG90舵机等。 主要功能: 系统运行后…...

【Windows】执行tasklist/taskkill提示“错误:找不到”或者“ERROR: not found”的解决方案
原因 由于WinMgmt异常导致起不来,而WinMgmt是SVCHOST进程中的WMI服务,解决这个问题需要停止之后再重新启动。 WinMgmt是Windows 2000客户端管理的核心组件,当客户端应用程序连接或当管理程序需要它本身的服务时,这个进程就会初始…...

MS2630——Sub-1 GHz、低噪声放大器芯片
产品简述 MS2630 是一款 Sub-1 GHz 低功耗、低噪声放大器 (LNA) 芯 片。芯片采用先进制造工艺,采用 SOT23-6 的封装形式。 主要特点 ◼ 典型噪声系数: 1.57dB ◼ 典型功率增益: 16.3dB ◼ 典型输出 P1dB : -9.2dBm…...

车载以太网-数据链路层-MAC
文章目录 车载以太网MAC(Media Access Control)车载以太网MAC帧格式以太网MAC帧报文示例车载以太网MAC层测试内容车载以太网MAC(Media Access Control) 车载以太网MAC(Media Access Control)是一种用于车载通信系统的以太网硬件地址,用于在物理层上识别和管理数据包的传…...

Tomcat源码分析
Tomcat源码分析与实例 Tomcat是一个开源的Java Web服务器,它提供了一种简单的方式来部署和运行Java Web应用程序。本文将详细介绍Tomcat的源码分析和实例。 1. Tomcat源码分析 1.1 目录结构 Tomcat的源码目录结构如下: tomcat-x.y.z/ ├── bin/ ├…...
计算机视觉面试题-02
图像处理和计算机视觉基础 什么是图像滤波?有哪些常见的图像滤波器? 图像滤波是一种通过在图像上应用滤波器(卷积核)来改变图像外观或提取图像特征的图像处理技术。滤波器通常是一个小的矩阵,通过在图像上进行卷积…...
力扣日记11.27-【二叉树篇】二叉树的最大深度
力扣日记:【二叉树篇】二叉树的最大深度 日期:2023.11.27 参考:代码随想录、力扣 104. 二叉树的最大深度 题目描述 难度: 给定一个二叉树 root ,返回其最大深度。 二叉树的 最大深度 是指从根节点到最远叶子节点的最…...
【数据结构】树的概念以及二叉树
目录 1 树概念及结构 1.1 树的概念 1.3 树的存储 2 二叉树的概念及结构 2.1 概念 2.2 特殊的二叉树 2.3 二叉树的性质 2.4 二叉树的存储结构 1 树概念及结构 1.1 树的概念 树是一种非线性的数据结构,它是由n(n>0)个有限结点组…...
软件测试职业规划导图
公司开发的产品专业性较强,软件测试人员需要有很强的专业知识,现在软件测试人员发展出现了一种测试管理者不愿意看到的景象: 1、开发技术较强的软件测试人员转向了软件开发(非测试工具开发); 2、业务能力较强的测试人员转向了软件…...
360压缩安装一半不动了?一分钟解决!
360压缩软件是我们常用的压缩软件,但是常常会遇到压缩安装到一半停止的情况,下面提供了一些可能的原因和解决办法,大家可以进行尝试~ 方法一:关闭防火墙和杀毒软件 有时候,防火墙和杀毒软件可能会阻止360压缩的安装过…...
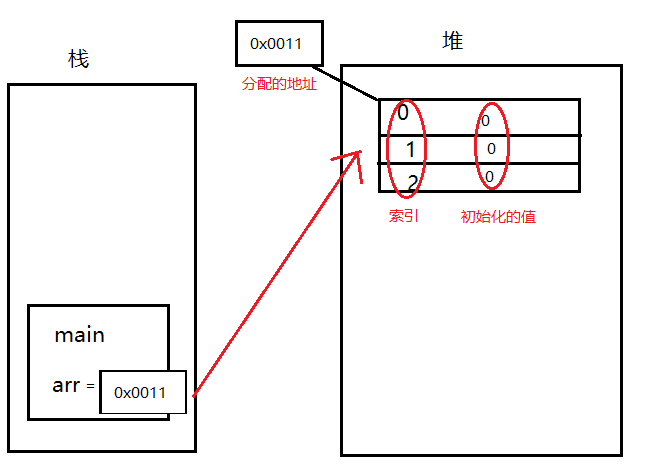
堆和栈的区别 重点来说一下堆和栈;堆与栈之间的联系
文章目录 堆和栈的区别重点来说一下堆和栈:那么堆和栈是怎么联系起来的呢? 堆与栈的区别 很明显: 今天来聊一聊java中的堆和栈,工作当中这两个也是经常遇到的,知识我们没有去注意理论上的这些内容,今天就来分享一下。…...

python 批量将图片存入excel单元格内
python 批量将图片存入excel单元格 示例代码1示例代码2 示例代码1 https://blog.csdn.net/wuyoudeyuer/article/details/128185284 # -*- coding: utf-8 -*- # Time : 2022-12-05 # Author : Carl_DJ 实现功能:在excel中,对应的名称后面,…...

Nginx常见的中间件漏洞
目录 1、Nginx文件名逻辑漏洞 2、Nginx解析漏洞 3、Nginx越权读取缓存漏洞 这里需要的漏洞环境可以看:Nginx 配置错误导致的漏洞-CSDN博客 1、Nginx文件名逻辑漏洞 该漏洞利用条件有两个: Nginx 0.8.41 ~ 1.4.3 / 1.5.0 ~ 1.5.7 php-fpm.conf中的s…...

Linux C语言 27-递归
Linux C语言 27-递归 本节关键字:C语言 递归 相关C库函数:main、printf 什么是递归? 在C语言中,程序调用自身的编程技巧称为递归(recursion)。递归从字面上可以理解为“递去归来”。 使用递归的优缺点 …...

redis运维(二十一)redis 的扩展应用 lua(三)
一 redis 的扩展应用 lua redis加载lua脚本文件 ① 调试lua脚本 redis-cli 通过管道 --pipe 快速导入数据到redis中 ② 预加载方式 1、错误方式 2、正确方式 "案例讲解" ③ 一次性加载 执行命令: redis-cli -a 密码 --eval Lua脚本路径 key …...

如何科学地划分医学图像数据集
在进行医学图像分类任务时,如何科学地划分数据集是一个重要的问题。这个问题的答案取决于你的数据特性和实验目标。一般来说,有两种常见的数据划分方法:按照比例划分和按照病例划分。 按照比例划分 按照比例划分是一种常见的方法,…...

【开源】基于Vue+SpringBoot的食品生产管理系统
项目编号: S 044 ,文末获取源码。 \color{red}{项目编号:S044,文末获取源码。} 项目编号:S044,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 加工厂管理模块2.2 客户管理模块2.3…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

mac:大模型系列测试
0 MAC 前几天经过学生优惠以及国补17K入手了mac studio,然后这两天亲自测试其模型行运用能力如何,是否支持微调、推理速度等能力。下面进入正文。 1 mac 与 unsloth 按照下面的进行安装以及测试,是可以跑通文章里面的代码。训练速度也是很快的。 注意…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...
