C#,《小白学程序》第二十二课:大数的乘法(BigInteger Multiply)
1 文本格式
using System;
using System.Linq;
using System.Text;
using System.Collections.Generic;
/// <summary>
/// 大数的(加减乘除)四则运算、阶乘运算
/// 乘法计算包括小学生算法、Karatsuba和Toom-Cook3算法
/// </summary>
public static class BigInteger_Utility
{
/// <summary>
/// 记录 加减乘除 的运算次数
/// </summary>
public static int[] operations { get; set; } = new int[] { 0, 0, 0, 0 };
/// <summary>
/// 《小白学程序》第十九课:随机数(Random)第六,随机生成任意长度的大数(BigInteger)
/// 一般可将超过9位数的数字成为“大数”。
/// 两个大数之间的四则运算用于密码学、高精度计算等应用。
/// 位数很多的浮点数可转为大数,再逆转即可。
/// </summary>
/// <param name="n"></param>
/// <returns></returns>
public static string rand(int n)
{
// 随机数发生器
Random rnd = new Random();
StringBuilder sb = new StringBuilder();
// 第一个数字不能为0,故:0-8之间的随机数+ 1 = 1-9
sb.Append((rnd.Next(9) + 1).ToString());
// 后面 n-1 个数字为 0-9;从 1 开始计数
for (int i = 1; i < n; i++)
{
sb.Append((rnd.Next(10)).ToString());
}
return sb.ToString();
}
/// <summary>
/// 字符串型的数字转为数组
/// 低位(右)在前,比如 "123" , n=6 存为 3,2,1,_,_,_
/// n 可能大于 a 的长度;剩余位置留出来用于 进位 等。
/// </summary>
/// <param name="a"></param>
/// <param name="n">最大位数,后面留0</param>
/// <returns></returns>
public static int[] string_to_digitals(string a, int n)
{
// 字符串 转为 “字符数组”
char[] c = a.ToCharArray();
// 存储数字的数组
int[] d = new int[n];
// 从最右端(个位)数字开始,转存为数字数组,参与后面的计算
for (int i = a.Length - 1, j = 0; i >= 0; i--)
{
// 跳过数字前面可能有的 - 号
if (a[i] == '-') continue;
// '0' 字符是最小的数字字符
// 数值 = 字符 - '0' ;
d[j++] = a[i] - '0';
}
return d;
}
/// <summary>
/// 数组型数字转为字符串型
/// 低位(右)在前,比如 3,2,1,_,_,_ 转为 "123", n=6
/// 这是前面 string_to_digitals 的反向计算函数
/// n 可能大于 d 的长度;剩余位置留出来用于 进位 等。
/// </summary>
/// <param name="d"></param>
/// <returns></returns>
public static string digitals_to_string(int[] d)
{
int n = d.Length;
// 数字数组 d 含有一些无效的数组;
// 因此,先从最右段开始去除无效的位置
int k = n - 1;
//for (; (k >= 0) && (d[k] == 0); k--) ;
while ((k >= 0) && (d[k] == 0)) k--;
// 找到有效位置后,开始组合字符串;
if (k >= 0)
{
StringBuilder sb = new StringBuilder();
for (; k >= 0; k--) sb.Append(d[k]);
return sb.ToString();
}
else
{
return "0";
}
}
/// <summary>
/// 《小白学程序》第二十二课:大数(BigInteger)的四则运算之三,乘法
/// 大数乘法 c = a * b
/// 本算法与小学生算法基本一致,主要的区别是:
/// 小学生算法每两个位数的数字相乘后立即进位;
/// 而本程序则是先计算全部相乘,最后统一进位。
/// 可能出乎大家的意料!虽然很多大牛发明了多种算法,
/// 如果进行编译器自动优化,该算法居然经常是最快的。
/// </summary>
/// <param name="a"></param>
/// <param name="b"></param>
/// <returns></returns>
public static string big_integer_multiply(string a, string b)
{
int na = a.Length;
int nb = b.Length;
int n = na + nb + 1;
int[] da = string_to_digitals(a, n);
int[] db = string_to_digitals(b, n);
// 乘数的每一位 乘以 被乘数
int[] dc = new int[n];
for (int i = 0; i < na; i++)
{
for (int j = 0; j < nb; j++)
{
dc[i + j] += da[i] * db[j];
}
}
// 所有位置进位
for (int i = 0; i < n; i++)
{
if (dc[i] >= 10)
{
dc[i + 1] += (dc[i] / 10);
dc[i] %= 10;
}
}
return digitals_to_string(dc);
}
}
2 代码格式
using System;
using System.Linq;
using System.Text;
using System.Collections.Generic;/// <summary>
/// 大数的(加减乘除)四则运算、阶乘运算
/// 乘法计算包括小学生算法、Karatsuba和Toom-Cook3算法
/// </summary>
public static class BigInteger_Utility
{/// <summary>/// 记录 加减乘除 的运算次数/// </summary>public static int[] operations { get; set; } = new int[] { 0, 0, 0, 0 };/// <summary>/// 《小白学程序》第十九课:随机数(Random)第六,随机生成任意长度的大数(BigInteger)/// 一般可将超过9位数的数字成为“大数”。/// 两个大数之间的四则运算用于密码学、高精度计算等应用。/// 位数很多的浮点数可转为大数,再逆转即可。/// </summary>/// <param name="n"></param>/// <returns></returns>public static string rand(int n){// 随机数发生器Random rnd = new Random();StringBuilder sb = new StringBuilder();// 第一个数字不能为0,故:0-8之间的随机数+ 1 = 1-9sb.Append((rnd.Next(9) + 1).ToString());// 后面 n-1 个数字为 0-9;从 1 开始计数for (int i = 1; i < n; i++){sb.Append((rnd.Next(10)).ToString());}return sb.ToString();}/// <summary>/// 字符串型的数字转为数组/// 低位(右)在前,比如 "123" , n=6 存为 3,2,1,_,_,_/// n 可能大于 a 的长度;剩余位置留出来用于 进位 等。/// </summary>/// <param name="a"></param>/// <param name="n">最大位数,后面留0</param>/// <returns></returns>public static int[] string_to_digitals(string a, int n){// 字符串 转为 “字符数组”char[] c = a.ToCharArray();// 存储数字的数组int[] d = new int[n];// 从最右端(个位)数字开始,转存为数字数组,参与后面的计算for (int i = a.Length - 1, j = 0; i >= 0; i--){// 跳过数字前面可能有的 - 号if (a[i] == '-') continue;// '0' 字符是最小的数字字符// 数值 = 字符 - '0' ;d[j++] = a[i] - '0';}return d;}/// <summary>/// 数组型数字转为字符串型/// 低位(右)在前,比如 3,2,1,_,_,_ 转为 "123", n=6/// 这是前面 string_to_digitals 的反向计算函数/// n 可能大于 d 的长度;剩余位置留出来用于 进位 等。/// </summary>/// <param name="d"></param>/// <returns></returns>public static string digitals_to_string(int[] d){int n = d.Length;// 数字数组 d 含有一些无效的数组;// 因此,先从最右段开始去除无效的位置int k = n - 1;//for (; (k >= 0) && (d[k] == 0); k--) ;while ((k >= 0) && (d[k] == 0)) k--;// 找到有效位置后,开始组合字符串;if (k >= 0){StringBuilder sb = new StringBuilder();for (; k >= 0; k--) sb.Append(d[k]);return sb.ToString();}else{return "0";}}/// <summary>/// 《小白学程序》第二十二课:大数(BigInteger)的四则运算之三,乘法/// 大数乘法 c = a * b/// 本算法与小学生算法基本一致,主要的区别是:/// 小学生算法每两个位数的数字相乘后立即进位;/// 而本程序则是先计算全部相乘,最后统一进位。/// 可能出乎大家的意料!虽然很多大牛发明了多种算法,/// 如果进行编译器自动优化,该算法居然经常是最快的。/// </summary>/// <param name="a"></param>/// <param name="b"></param>/// <returns></returns>public static string big_integer_multiply(string a, string b){int na = a.Length;int nb = b.Length;int n = na + nb + 1;int[] da = string_to_digitals(a, n);int[] db = string_to_digitals(b, n);// 乘数的每一位 乘以 被乘数int[] dc = new int[n];for (int i = 0; i < na; i++){for (int j = 0; j < nb; j++){dc[i + j] += da[i] * db[j];}}// 所有位置进位for (int i = 0; i < n; i++){if (dc[i] >= 10){dc[i + 1] += (dc[i] / 10);dc[i] %= 10;}}return digitals_to_string(dc);}
}
3 计算结果
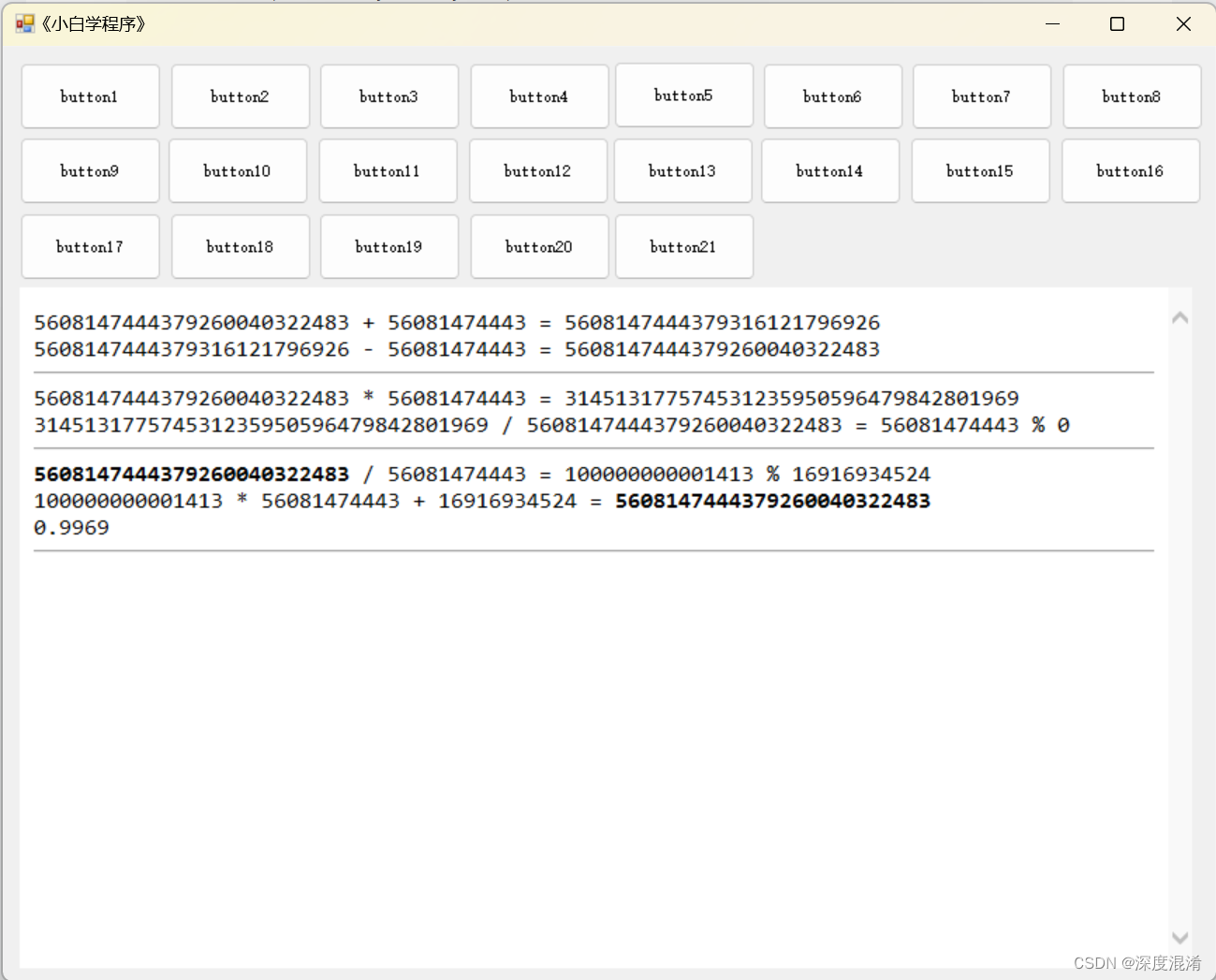
相关文章:

C#,《小白学程序》第二十二课:大数的乘法(BigInteger Multiply)
1 文本格式 using System; using System.Linq; using System.Text; using System.Collections.Generic; /// <summary> /// 大数的(加减乘除)四则运算、阶乘运算 /// 乘法计算包括小学生算法、Karatsuba和Toom-Cook3算法 /// </summary> p…...
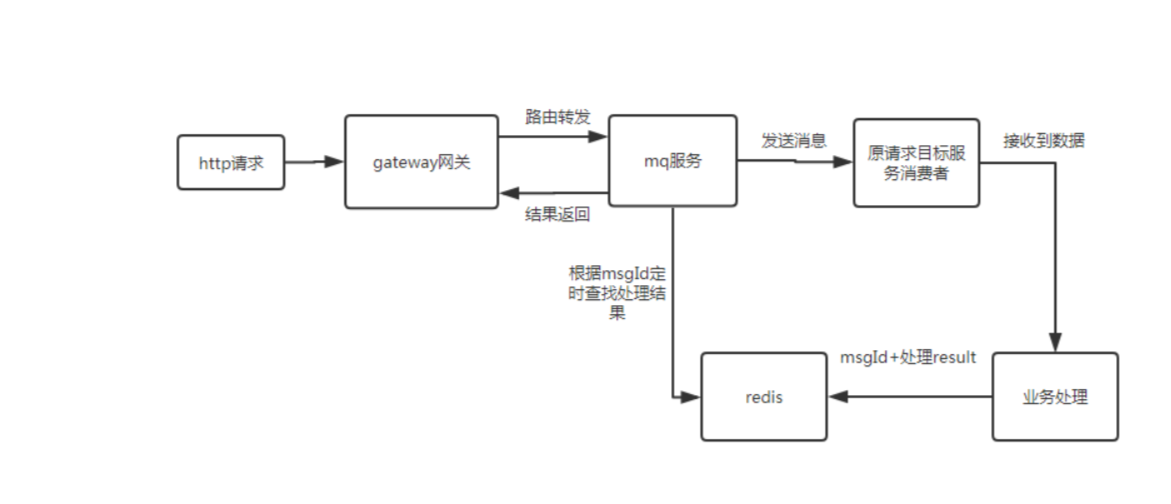
kafka,RabbitMQ,RocketMQ,他们之间的区别,架构,如何保证消息的不丢失,保证不重复消费,保证消息的有序性
文章目录 Kafka、RabbitMQ、RocketMQ 之间的区别是什么?性能数据可靠性服务可用性功能 RabbitMQ如何保证消息不丢失?Kafka 的架构说一下?Kafka 怎么保证消息是有序的?Kafka 怎么解决重复消费?Kafka 怎么保证消息不丢失…...

uni-app中vue3+setup实现下拉刷新、上拉加载更多效果
在小程序或各类app中,下拉刷新和上拉加载更多是极为常见和使用非常频繁的两个功能,通过对这两个功能的合理使用可以极大的方便用户进行操作。 合理的设计逻辑才能更容易挽留住用户,因为这些细节性的小功能点就变得极为重要起来。 那么在uni…...

微服务实战系列之Nginx(技巧篇)
前言 今天北京早晨竟然飘了一些“雪花”,定睛一看,似雪非雪,像泡沫球一样,原来那叫“霰”。 自然中,雨雪霜露雾,因为出场太频繁,认识门槛较低,自然不费吹灰之力,即可享受…...

好工具|datamap,一个好用的地图可视化Excel插件,在Excel中实现地理编码、拾取坐标
在做VRP相关研究的时候,需要对地图数据做很多处理,比如地理编码,根据“重庆市沙坪坝区沙正街174号”这样的一个文本地址知道他的经纬度;再比如绘制一些散点图,根据某个位置的经纬度在地图上把它标注出来。还有有的时候…...

Java——继承
继承是面向对象编程的三大特征之一,它让我们更加容易实现对已有类的扩展、更加容易实现对现实世界的建模。 继承有两个主要作用: 代码复用,更加容易实现类的扩展方便建模 继承的实现 继承让我们更加容易实现对类的扩展。比如我们定义了人…...

十、sdl显示yuv图片
前言 SDL中内置加载BMP的API,使用起来会更加简单,便于初学者学习使用SDL 如果需要加载JPG、PNG等其他格式的图片,可以使用第三方库:SDL_image 测试环境: ffmpeg的4.3.2自行编译版本windows环境qt5.12sdl2.0.22&…...

Docker Nginx容器部署vue项目
Docker Nginx容器部署vue项目 文章目录 Docker Nginx容器部署vue项目1. 前提2. 下载nginx镜像3. 编写nginx.conf配置文件4. 编写构建命令5. vue项目上传 1. 前提 Docker服务已部署 2. 下载nginx镜像 首先查看有没有nginx镜像 docker images没有的情况下再进行下载 docker …...
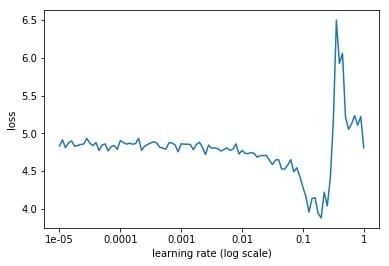
【深度学习】如何找到最优学习率
经过了大量炼丹的同学都知道,超参数是一个非常玄乎的东西,比如batch size,学习率等,这些东西的设定并没有什么规律和原因,论文中设定的超参数一般都是靠经验决定的。但是超参数往往又特别重要,比如学习率&a…...
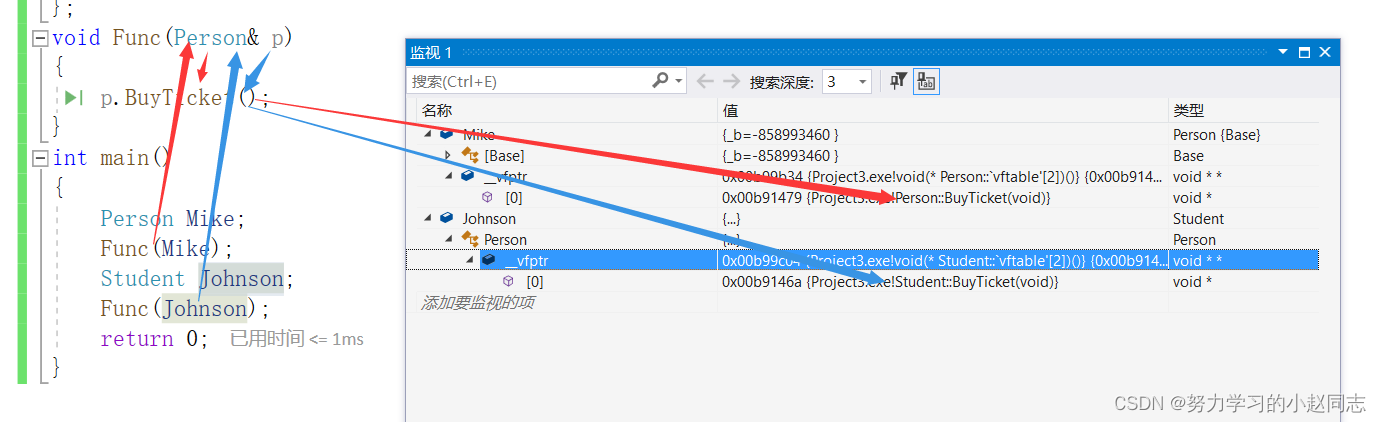
详解—C++三大特性——多态
目录 一. 多态的概念 1.1 概念 二. 多态的定义及实现 2.1多态的构成条件 2.2 虚函数 2.3虚函数的重写 2.3.1虚函数重写的两个例外: 1. 协变(基类与派生类虚函数返回值类型不同) 2. 析构函数的重写(基类与派生类析构函数的名字不同) 2.4 C11 override 和 f…...

用idea搭建一个spring cloud微服务项目
以下是使用 IntelliJ IDEA 搭建 Spring Cloud 微服务项目的步骤: 创建一个新的 Maven 项目。 在 pom.xml 文件中添加以下依赖: <dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-…...
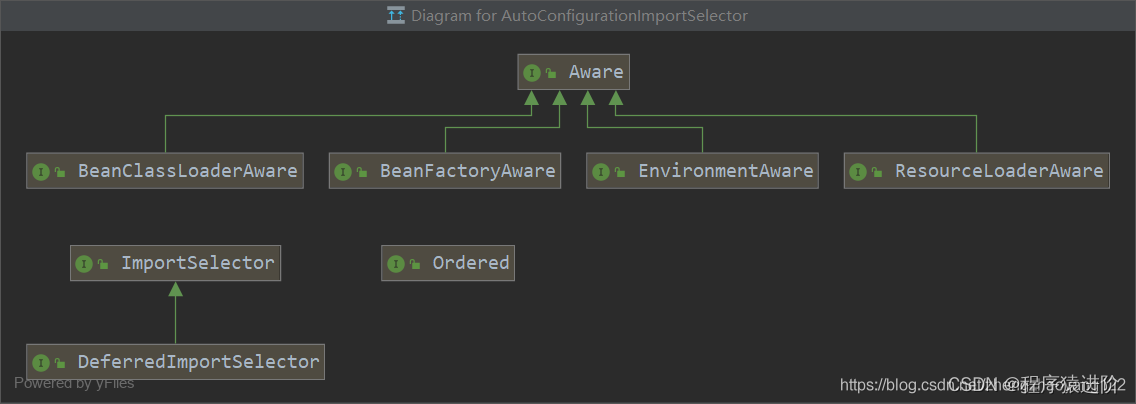
SpringBoot——启动类的原理
优质博文:IT-BLOG-CN SpringBoot启动类上使用SpringBootApplication注解,该注解是一个组合注解,包含多个其它注解。和类定义SpringApplication.run要揭开SpringBoot的神秘面纱,我们要从这两位开始就可以了。 SpringBootApplicati…...
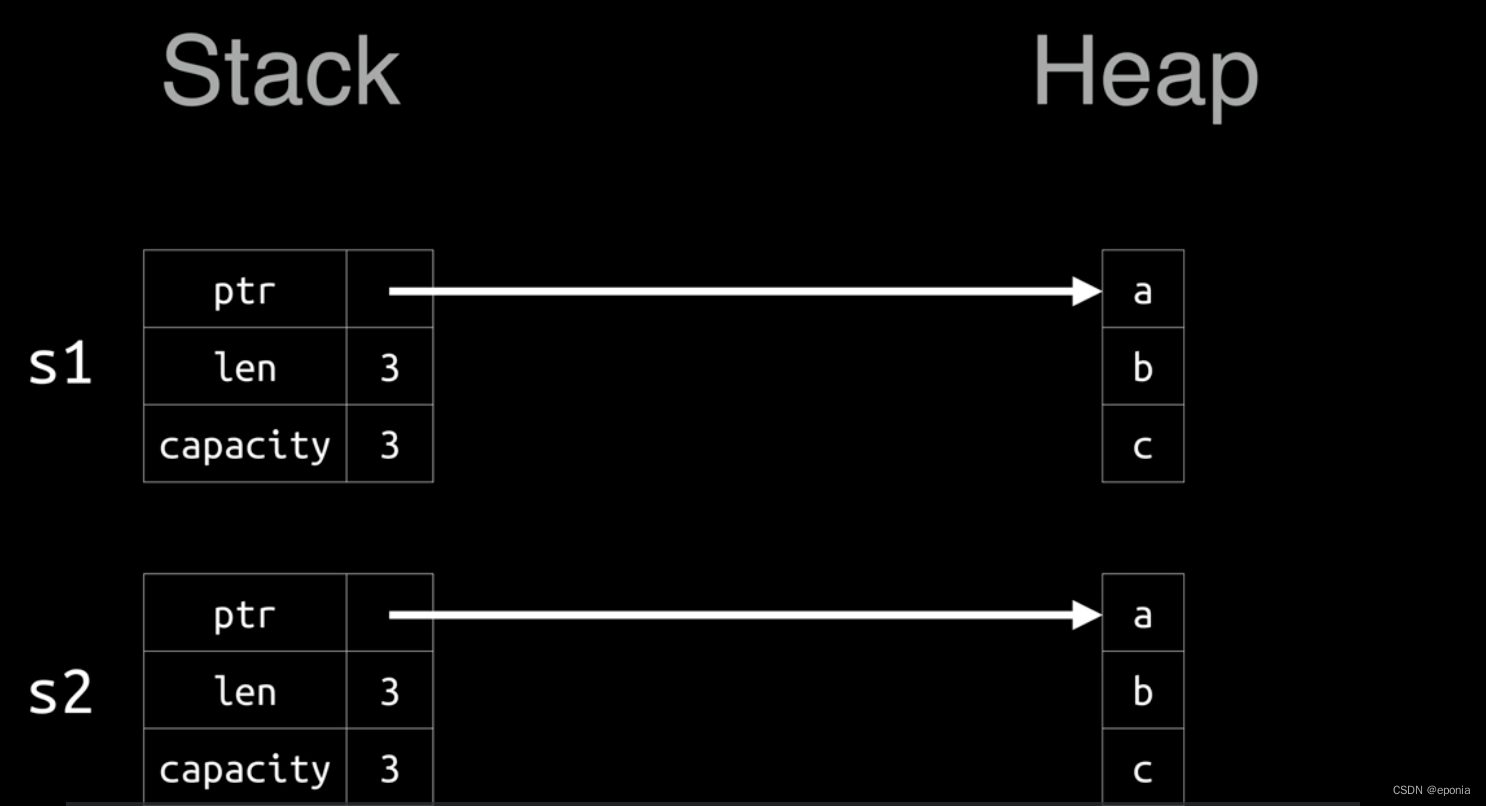
Rust语言入门教程(七) - 所有权系统
所有权系统是Rust敢于声称自己为一门内存安全语言的底气来源,也是让Rust成为一门与众不同的语言的所在之处。也正是因为这个特别的所有权系统,才使得编译器能够提前暴露代码中的错误,并给出我们必要且精准的错误提示。 所有权系统的三个规则…...
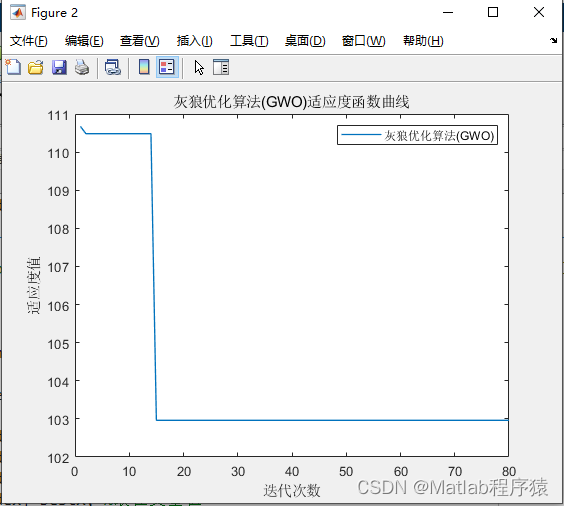
【MATLAB源码-第89期】基于matlab的灰狼优化算法(GWO)无人机三维路径规划,输出做短路径图和适应度曲线
操作环境: MATLAB 2022a 1、算法描述 灰狼优化算法(Grey Wolf Optimizer, GWO)是一种模仿灰狼捕食行为的优化算法。灰狼是群居动物,有着严格的社会等级结构。在灰狼群体中,通常有三个等级:首领ÿ…...

线程池的饱和策略有哪些?
线程池的饱和策略是指当线程池中的任务队列已满时,线程池如何处理新提交的任务。常见的饱和策略有以下几种: 阻塞策略 阻塞策略是指当线程池中的任务队列已满时,新提交的任务会等待队列中有空闲位置后再执行。这种策略可以避免过多的任务被…...

Git设置多个仓库同时推送
Git设置多个仓库同时推送 添加 在Git中,有时我们需要将同一份代码推送到不同的远程仓库,只是URL地址不同。 下面是一种优化的方法来设置多个仓库同时推送: # 添加一个新的远程仓库 git remote set-url --add origin2 新的仓库地址这样&am…...

前端入职环境安装
前端入职 后环境安装 ,内函 nodenvmgit微信开发者工具vscode 的安装包 一.node安装-js运行环境 1.node下载,下载地址Node.js 2.配置淘宝镜像 npm config set registry https://registry.npmmirror.com/ 3.查看配置 npm config list 二.nvm安装-切…...
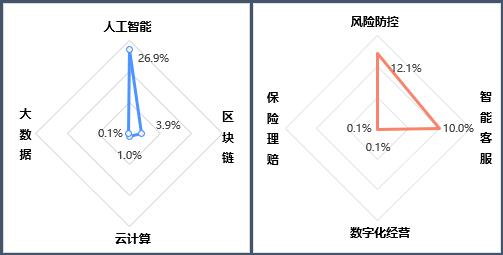
《金融科技行业2023年专利分析白皮书》发布——科技变革金融,专利助力行业发展
金融是国民经济的血脉,是国家核心竞争力的重要组成部分,金融高质量发展成为2023年中央金融工作的重要议题。《中国金融科技调查报告》中指出,我国金融服务业在科技的助力下,从1.0时代的“信息科技金融”、2.0时代的“互联网金融”…...

Introducing the Arm architecture
快速链接: . 👉👉👉 个人博客笔记导读目录(全部) 👈👈👈 付费专栏-付费课程 【购买须知】:【精选】ARMv8/ARMv9架构入门到精通-[目录] 👈👈👈 — 适合小白入门【目录】ARMv8/ARMv9架构高级进阶-[目录]👈👈👈 — 高级进阶、小白勿买【加群】ARM/TEE…...

Python 使用SQLAlchemy数据库模块
SQLAlchemy 是用Python编程语言开发的一个开源项目,它提供了SQL工具包和ORM对象关系映射工具,使用MIT许可证发行,SQLAlchemy 提供高效和高性能的数据库访问,实现了完整的企业级持久模型。 ORM(对象关系映射࿰…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...

CppCon 2015 学习:Time Programming Fundamentals
Civil Time 公历时间 特点: 共 6 个字段: Year(年)Month(月)Day(日)Hour(小时)Minute(分钟)Second(秒) 表示…...

