每日一题--寻找重复数
蝶恋花-王国维
阅尽天涯离别苦,
不道归来,零落花如许。
花底相看无一语,绿窗春与天俱莫。
待把相思灯下诉,一缕新欢,旧恨千千缕。
最是人间留不住,朱颜辞镜花辞树。

目录
题目描述:
思路分析:
方法及时间复杂度:
法一 排序数组(暴力解法):
法二 哈希表
法三 二分查找(经典解法)
法四 快慢指针
法五 二进制(烧脑解法)
个人总结:
题目描述:

287. 寻找重复数 - 力扣(LeetCode)
思路分析:
在一个数组中查找唯一重复的元素,可以用很多解法,立马想到的便是哈希表。将数组元素插入哈希表,然后查找哈希表,找到了就返回该数
方法及时间复杂度:
法一 排序数组(暴力解法):
将数组进行排序,这样重复的元素一定相邻,然后遍历排序后的数组就行。代码如下:

int cmp(const void*a,const void*b){return *(int*)a-*(int*)b;
}
int findDuplicate(int* nums, int numsSize) {qsort(nums,numsSize,sizeof(int),cmp);for(int i=1;i<numsSize;++i){if(nums[i]==nums[i-1]){return nums[i];}}return -1;
}时间复杂度O(nlogn) 排序的时间nlogn
空间复杂度O(1)
法二 哈希表
利用哈希表查找哈希表中存在的元素,即数组重复的元素。可以使用c++容器的哈希集合unordered_set,这里用c语言数组模拟了一个哈希表。代码如下:
int findDuplicate(int* nums, int numsSize) {int hash[100001]={0};//初始化哈希表所有元素为0for(int i=0;i<numsSize;++i){if(hash[nums[i]]){//查找哈希表中是否存在该元素return nums[i];}hash[nums[i]]++;}return -1;
}时间复杂度O(n)
空间复杂度O(n) 空间换时间了属于是
法三 二分查找(经典解法)
用此方法前先弄清楚什么是鸽巢原理。
鸽巢原理:也称为抽屉原理,是一个基本的数学原理,这个原理的经典解释是,就像将若干只鸽子放在若干个鸽巢中一样,如果鸽子的数量大于鸽巢的数量,那么至少有一个鸽巢中放了两只鸽子。

这里抽象成二分查找那个装有两只鸽子的鸽巢
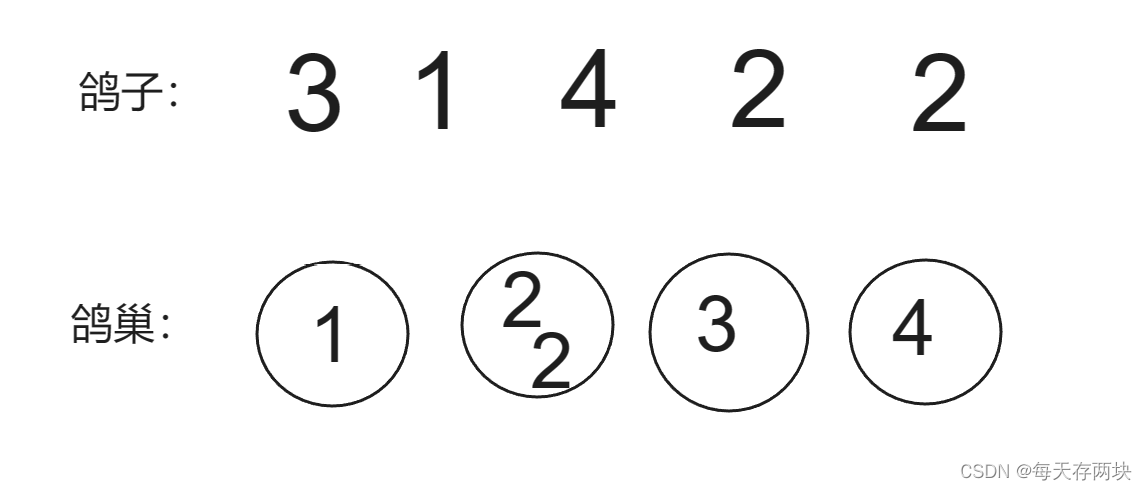
二分查找的区间很明显就是【1,n-1】,n为数组长度。查找中点mid(先猜一个鸽巢),遍历数组并记录<=mid的数,如果<=mid的数大于mid说明这个有着两只鸽子的鸽巢在左区间,反之,如果<=mid的数小于等于mid,就在右区间。直到left==right时,这个鸽巢就是有着两只鸽子的鸽巢。
代码如下:
int findDuplicate(int* nums, int numsSize) {int left=1,right=numsSize-1;while(left<right){int mid=(left+right)>>1;int cnt=0;for(int i=0;i<numsSize;++i){if(nums[i]<=mid){cnt++;}}if(cnt>mid){right=mid;}else{left=mid+1;}}return left;
}时间复杂度O(nlogn) 二分查找时间复杂度 logn,然后每次查找都要遍历数组O(n)
空间复杂度O(1)
法四 快慢指针
下标向值引一条边,值向下标引一条边,从0开始沿着箭头走,逐渐就会进入一个环,环的入口就是重复的元素。
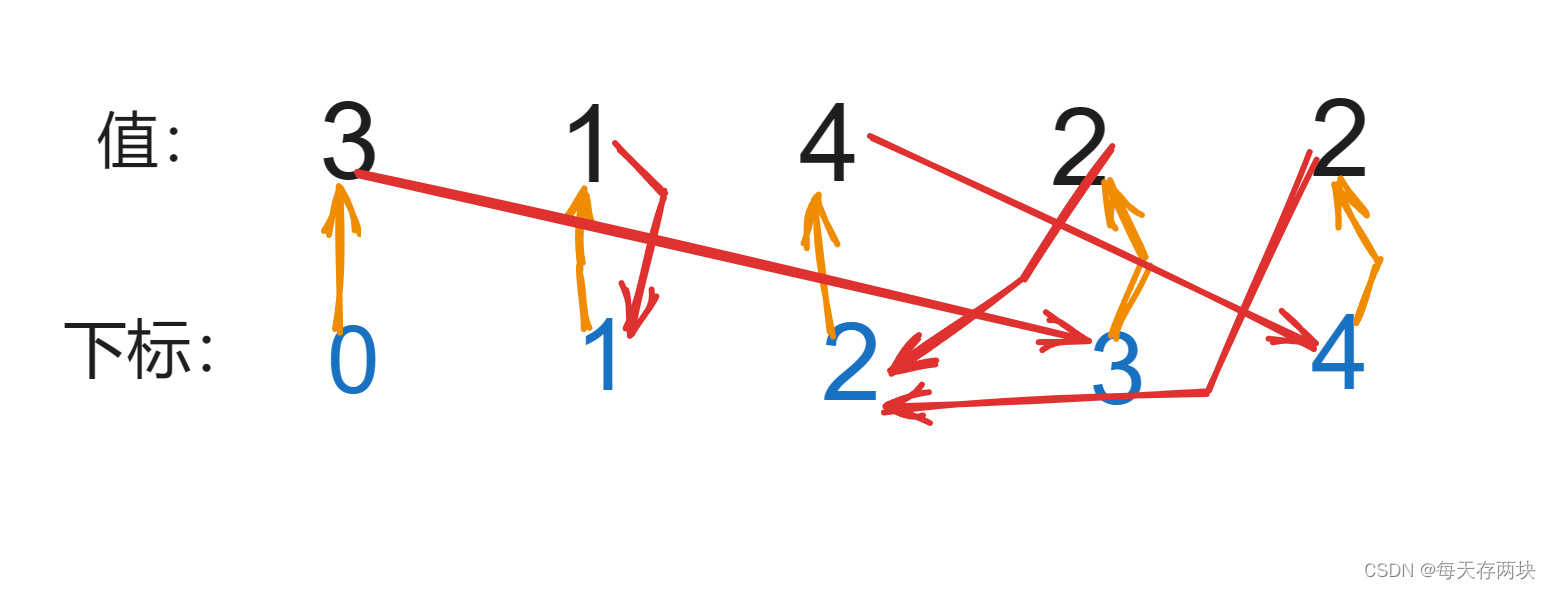
类似于环形链表,定义快指针fast,慢指针slow。慢指针每次走一步,快指针每次走两步,快指针会在环里追上慢指针,然后让快指针从0开始走,快慢指针同时走一步,相逢时就是环的入口,即重复元素。
代码如下:
int findDuplicate(int* nums, int numsSize) {int slow=0,fast=0;do{slow=nums[slow];fast=nums[nums[fast]];}while(slow!=fast);fast=0;while(slow!=fast){slow=nums[slow];fast=nums[fast];}return slow;
}时间复杂度O(n)
空间复杂度O(1)
法五 二进制(烧脑解法)
可以使用二进制位运算来解决此题。我们可以将数组 nums 中的每一个数字用二进制来表示,最多只需要 log(n) 位,其中 n 是数组 nums 的长度。
对于每一位 i,我们可以计算在此位上所有数字出现的次数之和。如果某一位上的出现次数之和大于 2,说明出现了重复的数字。
具体做法如下:
- 对于二进制的第 i 位,计算所有数字的二进制表示中第 i 位上出现 1 的次数之和(可以使用位运算和移位操作进行统计)。
- 如果第 i 位上出现 1 的次数之和大于 2,说明重复数字在此位上的值为 1,否则为 0。
- 将所有位上确定的二进制位还原成对应的十进制数字,即为重复的数字。
代码如下:
int findDuplicate(int* nums, int n) {int ans = 0;// 确定二进制下最高位是多少int bit_max = 31;while (!((n - 1) >> bit_max)) {bit_max -= 1;}for (int bit = 0; bit <= bit_max; ++bit) {int x = 0, y = 0;for (int i = 0; i < n; ++i) {if (nums[i] & (1 << bit)) {x += 1;}if (i >= 1 && (i & (1 << bit))) {y += 1;}}if (x > y) {ans |= 1 << bit;}}return ans;
}时间复杂度O(nlogn) 枚举二进制数的位数个数O(logn)
空间复杂度O(1)
个人总结:
二分查找的算法其实还可以优化。 有位大师曾经说过,完成比完美更重要。
相关文章:

每日一题--寻找重复数
蝶恋花-王国维 阅尽天涯离别苦, 不道归来,零落花如许。 花底相看无一语,绿窗春与天俱莫。 待把相思灯下诉, 一缕新欢,旧恨千千缕。 最是人间留不住,朱颜辞镜花辞树。 目录 题目描述: 思路分析…...
C#,《小白学程序》第二十二课:大数的乘法(BigInteger Multiply)
1 文本格式 using System; using System.Linq; using System.Text; using System.Collections.Generic; /// <summary> /// 大数的(加减乘除)四则运算、阶乘运算 /// 乘法计算包括小学生算法、Karatsuba和Toom-Cook3算法 /// </summary> p…...
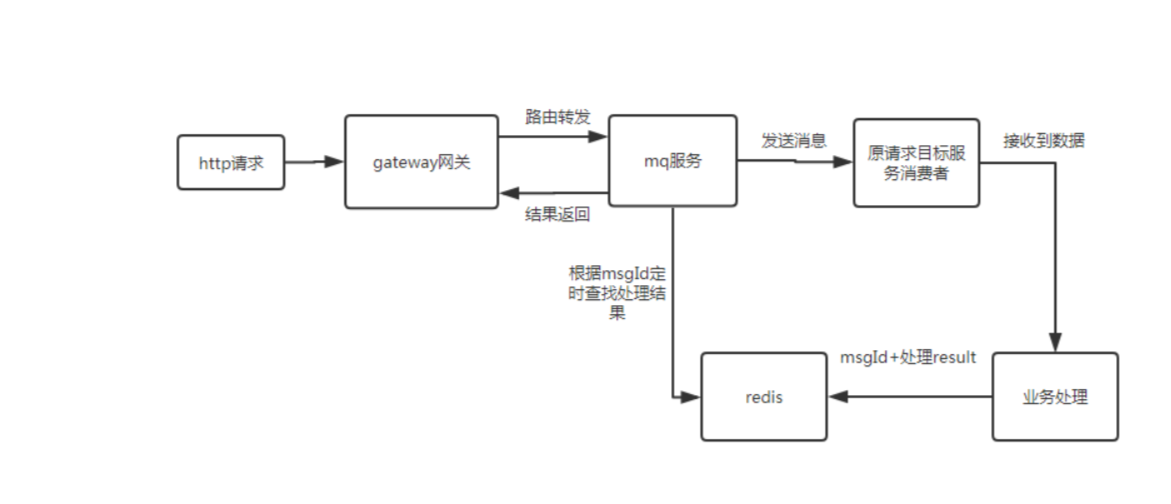
kafka,RabbitMQ,RocketMQ,他们之间的区别,架构,如何保证消息的不丢失,保证不重复消费,保证消息的有序性
文章目录 Kafka、RabbitMQ、RocketMQ 之间的区别是什么?性能数据可靠性服务可用性功能 RabbitMQ如何保证消息不丢失?Kafka 的架构说一下?Kafka 怎么保证消息是有序的?Kafka 怎么解决重复消费?Kafka 怎么保证消息不丢失…...

uni-app中vue3+setup实现下拉刷新、上拉加载更多效果
在小程序或各类app中,下拉刷新和上拉加载更多是极为常见和使用非常频繁的两个功能,通过对这两个功能的合理使用可以极大的方便用户进行操作。 合理的设计逻辑才能更容易挽留住用户,因为这些细节性的小功能点就变得极为重要起来。 那么在uni…...

微服务实战系列之Nginx(技巧篇)
前言 今天北京早晨竟然飘了一些“雪花”,定睛一看,似雪非雪,像泡沫球一样,原来那叫“霰”。 自然中,雨雪霜露雾,因为出场太频繁,认识门槛较低,自然不费吹灰之力,即可享受…...

好工具|datamap,一个好用的地图可视化Excel插件,在Excel中实现地理编码、拾取坐标
在做VRP相关研究的时候,需要对地图数据做很多处理,比如地理编码,根据“重庆市沙坪坝区沙正街174号”这样的一个文本地址知道他的经纬度;再比如绘制一些散点图,根据某个位置的经纬度在地图上把它标注出来。还有有的时候…...

Java——继承
继承是面向对象编程的三大特征之一,它让我们更加容易实现对已有类的扩展、更加容易实现对现实世界的建模。 继承有两个主要作用: 代码复用,更加容易实现类的扩展方便建模 继承的实现 继承让我们更加容易实现对类的扩展。比如我们定义了人…...

十、sdl显示yuv图片
前言 SDL中内置加载BMP的API,使用起来会更加简单,便于初学者学习使用SDL 如果需要加载JPG、PNG等其他格式的图片,可以使用第三方库:SDL_image 测试环境: ffmpeg的4.3.2自行编译版本windows环境qt5.12sdl2.0.22&…...

Docker Nginx容器部署vue项目
Docker Nginx容器部署vue项目 文章目录 Docker Nginx容器部署vue项目1. 前提2. 下载nginx镜像3. 编写nginx.conf配置文件4. 编写构建命令5. vue项目上传 1. 前提 Docker服务已部署 2. 下载nginx镜像 首先查看有没有nginx镜像 docker images没有的情况下再进行下载 docker …...
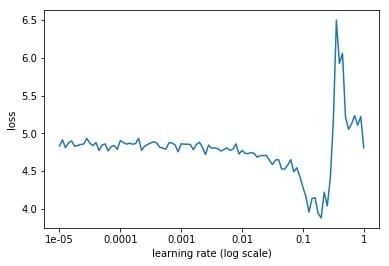
【深度学习】如何找到最优学习率
经过了大量炼丹的同学都知道,超参数是一个非常玄乎的东西,比如batch size,学习率等,这些东西的设定并没有什么规律和原因,论文中设定的超参数一般都是靠经验决定的。但是超参数往往又特别重要,比如学习率&a…...
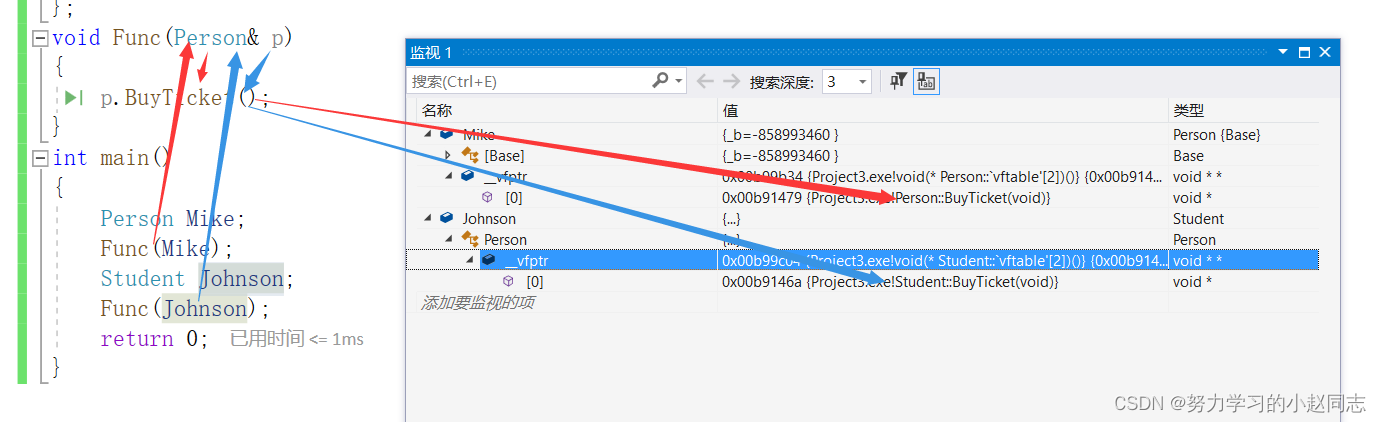
详解—C++三大特性——多态
目录 一. 多态的概念 1.1 概念 二. 多态的定义及实现 2.1多态的构成条件 2.2 虚函数 2.3虚函数的重写 2.3.1虚函数重写的两个例外: 1. 协变(基类与派生类虚函数返回值类型不同) 2. 析构函数的重写(基类与派生类析构函数的名字不同) 2.4 C11 override 和 f…...

用idea搭建一个spring cloud微服务项目
以下是使用 IntelliJ IDEA 搭建 Spring Cloud 微服务项目的步骤: 创建一个新的 Maven 项目。 在 pom.xml 文件中添加以下依赖: <dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-…...
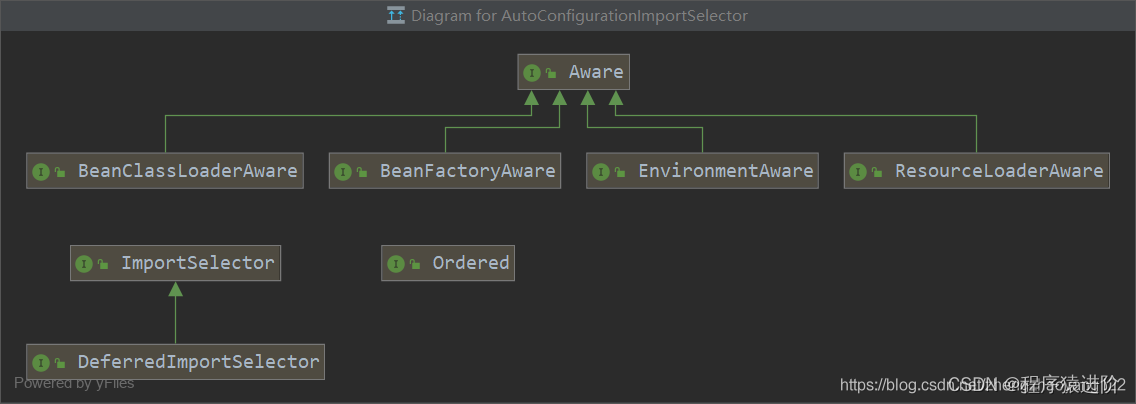
SpringBoot——启动类的原理
优质博文:IT-BLOG-CN SpringBoot启动类上使用SpringBootApplication注解,该注解是一个组合注解,包含多个其它注解。和类定义SpringApplication.run要揭开SpringBoot的神秘面纱,我们要从这两位开始就可以了。 SpringBootApplicati…...
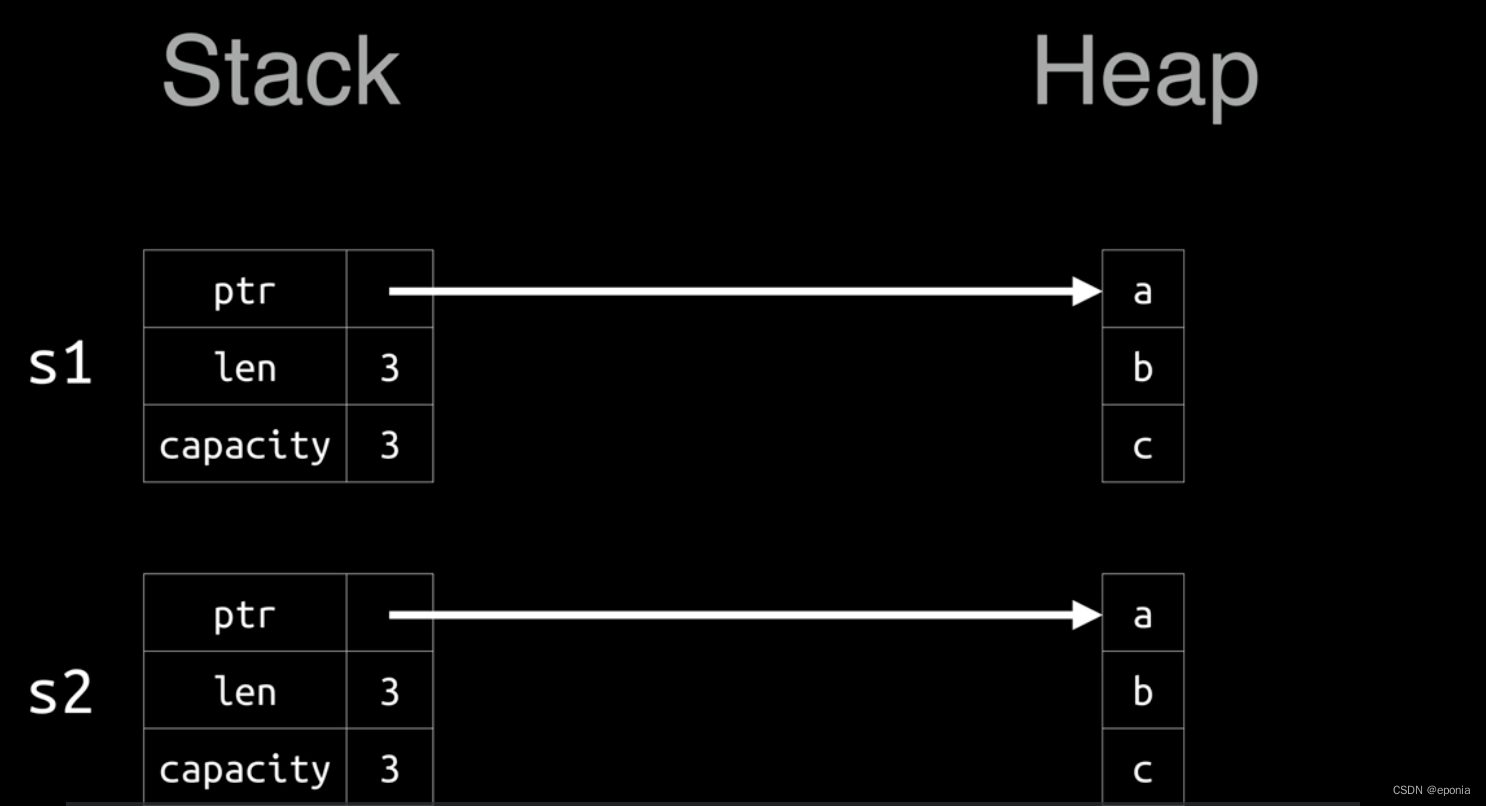
Rust语言入门教程(七) - 所有权系统
所有权系统是Rust敢于声称自己为一门内存安全语言的底气来源,也是让Rust成为一门与众不同的语言的所在之处。也正是因为这个特别的所有权系统,才使得编译器能够提前暴露代码中的错误,并给出我们必要且精准的错误提示。 所有权系统的三个规则…...
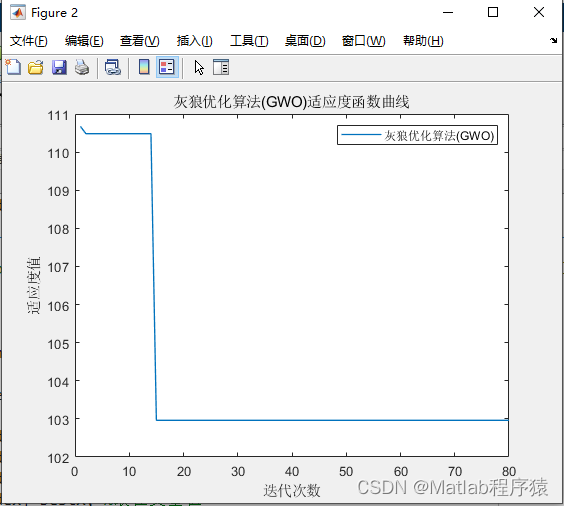
【MATLAB源码-第89期】基于matlab的灰狼优化算法(GWO)无人机三维路径规划,输出做短路径图和适应度曲线
操作环境: MATLAB 2022a 1、算法描述 灰狼优化算法(Grey Wolf Optimizer, GWO)是一种模仿灰狼捕食行为的优化算法。灰狼是群居动物,有着严格的社会等级结构。在灰狼群体中,通常有三个等级:首领ÿ…...

线程池的饱和策略有哪些?
线程池的饱和策略是指当线程池中的任务队列已满时,线程池如何处理新提交的任务。常见的饱和策略有以下几种: 阻塞策略 阻塞策略是指当线程池中的任务队列已满时,新提交的任务会等待队列中有空闲位置后再执行。这种策略可以避免过多的任务被…...

Git设置多个仓库同时推送
Git设置多个仓库同时推送 添加 在Git中,有时我们需要将同一份代码推送到不同的远程仓库,只是URL地址不同。 下面是一种优化的方法来设置多个仓库同时推送: # 添加一个新的远程仓库 git remote set-url --add origin2 新的仓库地址这样&am…...

前端入职环境安装
前端入职 后环境安装 ,内函 nodenvmgit微信开发者工具vscode 的安装包 一.node安装-js运行环境 1.node下载,下载地址Node.js 2.配置淘宝镜像 npm config set registry https://registry.npmmirror.com/ 3.查看配置 npm config list 二.nvm安装-切…...
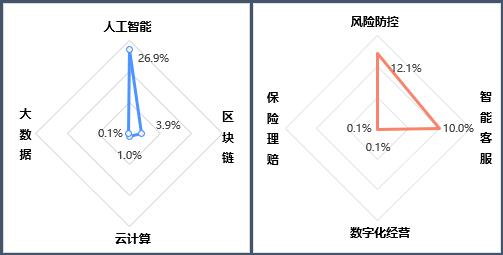
《金融科技行业2023年专利分析白皮书》发布——科技变革金融,专利助力行业发展
金融是国民经济的血脉,是国家核心竞争力的重要组成部分,金融高质量发展成为2023年中央金融工作的重要议题。《中国金融科技调查报告》中指出,我国金融服务业在科技的助力下,从1.0时代的“信息科技金融”、2.0时代的“互联网金融”…...

Introducing the Arm architecture
快速链接: . 👉👉👉 个人博客笔记导读目录(全部) 👈👈👈 付费专栏-付费课程 【购买须知】:【精选】ARMv8/ARMv9架构入门到精通-[目录] 👈👈👈 — 适合小白入门【目录】ARMv8/ARMv9架构高级进阶-[目录]👈👈👈 — 高级进阶、小白勿买【加群】ARM/TEE…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...
