策略算法与Actor-Critic网络
策略算法
教程链接
DataWhale强化学习课程JoyRL
https://johnjim0816.com/joyrl-book/#/ch7/main
策略梯度
与前面的基于价值的算法不同,这类算法直接对策略本身进行近似优化。
在这种情况下,我们可以将策略描述成一个带有参数 θ θ θ的连续函数,该函数将某个状态作为输入,输出的不再是某个确定性的离散动作,而是对应的动作概率分布,通常用 π θ ( a ∣ s ) \pi_{θ}(a|s) πθ(a∣s) 表示,称作随机性策略。
价值算法缺点
- 无法表示连续动作
由于 DQN 等算法是通过学习状态和动作的价值函数来间接指导策略的,因此它们只能处理离散动作空间的问题,无法表示连续动作空间的问题
- 高方差
基于价值的方法通常都是通过采样的方式来估计价值函数,这样会导致估计的方差很高,从而影响算法的收敛性。尽管一些 DQN 改进算法,通过改善经验回放、目标网络等方式,可以在一定程度上减小方差,但是这些方法并不能完全解决这个问题。
- 探索与利用的平衡问题
DQN 等算法在实现时通常选择贪心的确定性策略,而很多问题的最优策略是随机策略,即需要以不同的概率选择不同的动作。虽然可以通过 ϵ -greedy \epsilon\text{-greedy} ϵ-greedy 策略等方式来实现一定程度的随机策略,但是实际上这种方式并不是很理想,因为它并不能很好地平衡探索与利用的关系。
策略梯度算法
特点: 直接对策略进行优化算法,但是优化目标与基于价值一样,都是累积的价值期望 V ∗ ( s ) V^{*}(s) V∗(s)
轨迹产生的概率:
P θ ( τ ) = p ( s 0 ) π θ ( a 0 ∣ s 0 ) p ( s 1 ∣ s 0 , a 0 ) π θ ( a 1 ∣ s 1 ) p ( s 2 ∣ s 1 , a 1 ) ⋯ = p ( s 0 ) ∏ t = 0 T π θ ( a t ∣ s t ) p ( s t + 1 ∣ s t , a t ) (9.2) \tag{9.2} \begin{aligned} P_{\theta}(\tau) &=p(s_{0}) \pi_{\theta}(a_{0} | s_{0}) p(s_{1} | s_{0}, a_{0}) \pi_{\theta}(a_{1} | s_{1}) p(s_{2} | s_{1}, a_{1}) \cdots \\ &=p(s_{0}) \prod_{t=0}^{T} \pi_{\theta}\left(a_{t} | s_{t}\right) p\left(s_{t+1} | s_{t}, a_{t}\right) \end{aligned} Pθ(τ)=p(s0)πθ(a0∣s0)p(s1∣s0,a0)πθ(a1∣s1)p(s2∣s1,a1)⋯=p(s0)t=0∏Tπθ(at∣st)p(st+1∣st,at)(9.2)
基于全期望公式得到价值的期望公式
J ( π θ ) = E τ ∼ π θ [ R ( τ ) ] = P θ ( τ 1 ) R ( τ 1 ) + P θ ( τ 2 ) R ( τ 2 ) + ⋯ = ∫ τ P θ ( τ ) R ( τ ) = E τ ∼ P θ ( τ ) [ ∑ t r ( s t , a t ) ] (9.3) \tag{9.3} \begin{aligned} J(\pi_{\theta}) = \underset{\tau \sim \pi_\theta}{E}[R(\tau)] & = P_{\theta}(\tau_{1})R(\tau_{1})+P_{\theta}(\tau_{2})R(\tau_{2})+\cdots \\ &=\int_\tau P_{\theta}(\tau) R(\tau) \\ &=E_{\tau \sim P_\theta(\tau)}[\sum_t r(s_t, a_t)] \end{aligned} J(πθ)=τ∼πθE[R(τ)]=Pθ(τ1)R(τ1)+Pθ(τ2)R(τ2)+⋯=∫τPθ(τ)R(τ)=Eτ∼Pθ(τ)[t∑r(st,at)](9.3)
由于 R ( τ ) R(\tau) R(τ)与参数 θ \theta θ无关,一来问题就稍稍简化成了如何求解 P θ ( τ ) P_{\theta}(\tau) Pθ(τ) 的梯度了
后进行一系列推导
∇ θ P θ ( τ ) = P θ ( τ ) ∇ θ P θ ( τ ) P θ ( τ ) = P θ ( τ ) ∇ θ log P θ ( τ ) (9.4) \tag{9.4} \nabla_\theta P_{\theta}(\tau)= P_{\theta}(\tau) \frac{\nabla_\theta P_{\theta}(\tau)}{P_{\theta}(\tau) }= P_{\theta}(\tau) \nabla_\theta \log P_{\theta}(\tau) ∇θPθ(τ)=Pθ(τ)Pθ(τ)∇θPθ(τ)=Pθ(τ)∇θlogPθ(τ)(9.4)
log P θ ( τ ) = log p ( s 0 ) + ∑ t = 0 T ( log π θ ( a t ∣ s t ) + log p ( s t + 1 ∣ s t , a t ) ) (9.5) \tag{9.5} \log P_{\theta}(\tau)= \log p(s_{0}) + \sum_{t=0}^T(\log \pi_{\theta}(a_t \mid s_t)+\log p(s_{t+1} \mid s_t,a_t)) logPθ(τ)=logp(s0)+t=0∑T(logπθ(at∣st)+logp(st+1∣st,at))(9.5)
∇ θ log P θ ( τ ) = ∇ θ log ρ 0 ( s 0 ) + ∑ t = 0 T ( ∇ θ log π θ ( a t ∣ s t ) + ∇ θ log p ( s t + 1 ∣ s t , a t ) ) = 0 + ∑ t = 0 T ( ∇ θ log π θ ( a t ∣ s t ) + 0 ) = ∑ t = 0 T ∇ θ log π θ ( a t ∣ s t ) (9.6) \tag{9.6} \begin{aligned} \nabla_\theta \log P_{\theta}(\tau) &=\nabla_\theta \log \rho_0\left(s_0\right)+\sum_{t=0}^T\left(\nabla_\theta \log \pi_\theta\left(a_t \mid s_t\right)+\nabla_\theta \log p\left(s_{t+1} \mid s_t, a_t\right)\right) \\ &=0+\sum_{t=0}^T\left(\nabla_\theta \log \pi_\theta\left(a_t \mid s_t\right)+0\right) \\ &=\sum_{t=0}^T \nabla_\theta \log \pi_\theta\left(a_t \mid s_t\right) \end{aligned} ∇θlogPθ(τ)=∇θlogρ0(s0)+t=0∑T(∇θlogπθ(at∣st)+∇θlogp(st+1∣st,at))=0+t=0∑T(∇θlogπθ(at∣st)+0)=t=0∑T∇θlogπθ(at∣st)(9.6)
得到目标函数的梯度
∇ θ J ( π θ ) = ∇ θ E τ ∼ π θ [ R ( τ ) ] = ∇ θ ∫ τ P θ ( τ ) R ( τ ) = ∫ τ ∇ θ P θ ( τ ) R ( τ ) = ∫ τ P θ ( τ ) ∇ θ log P θ ( τ ) R ( τ ) = E τ ∼ π θ [ ∇ θ log P θ ( τ ) R ( τ ) ] = E τ ∼ π θ [ ∑ t = 0 T ∇ θ log π θ ( a t ∣ s t ) R ( τ ) ] (9.7) \tag{9.7} \begin{aligned} \nabla_\theta J\left(\pi_\theta\right) &=\nabla_\theta \underset{\tau \sim \pi_\theta}{\mathrm{E}}[R(\tau)] \\ &=\nabla_\theta \int_\tau P_{\theta}(\tau) R(\tau) \\ &=\int_\tau \nabla_\theta P_{\theta}(\tau) R(\tau) \\ &=\int_\tau P_{\theta}(\tau) \nabla_\theta \log P_{\theta}(\tau) R(\tau) \\ &=\underset{\tau \sim \pi_\theta}{\mathrm{E}}\left[\nabla_\theta \log P_{\theta}(\tau) R(\tau)\right]\\ &= \underset{\tau \sim \pi_\theta}{\mathrm{E}}\left[\sum_{t=0}^T \nabla_\theta \log \pi_\theta\left(a_t \mid s_t\right) R(\tau)\right] \end{aligned} ∇θJ(πθ)=∇θτ∼πθE[R(τ)]=∇θ∫τPθ(τ)R(τ)=∫τ∇θPθ(τ)R(τ)=∫τPθ(τ)∇θlogPθ(τ)R(τ)=τ∼πθE[∇θlogPθ(τ)R(τ)]=τ∼πθE[t=0∑T∇θlogπθ(at∣st)R(τ)](9.7)
蒙特卡洛策略梯度算法
由于环境的初始状态为随机的,智能体的每次采样动作也是随机的,从而导致每条轨迹可能不一样。考虑采样数量足够多的轨迹,然后利用这些轨迹的平均值来近似求解目标函数的梯度。
∇ J θ ≈ 1 N ∑ n = 1 N ∑ t = 1 T n G t n ∇ log π θ ( a t n ∣ s t n ) (9.8) \tag{9.8} \nabla J_{\theta} \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_{n}} G_{t}^{n} \nabla \log \pi_{\theta}\left(a_{t}^{n} \mid s_{t}^{n}\right) ∇Jθ≈N1n=1∑Nt=1∑TnGtn∇logπθ(atn∣stn)(9.8)
这里我们假定目标是使每回合的累积价值最大。
但是实际每回合的累积奖励或回报会受到很多因素的影响。后引入优势量来进行评估价值。
作业题
- 基于价值和基于策略的算法各有什么优缺点?
基于价值的算法的优点包括:
-
可以收敛到全局最优策略,而不是局部最优。
-
可以利用贪心策略或者epsilon-greedy策略来平衡探索和利用。
-
可以用于离散或者连续的状态空间。
基于价值的算法的缺点包括:
- 对于高维或者连续的动作空间,难以找到最优的动作。
- 需要存储和更新一个大的值函数表格或者近似函数,计算量较大。
- 不能很好地处理随机策略。
策略梯度算法优点:
- 适配连续动作空间。在将策略函数设计的时候我们已经展开过,这里不再赘述。
- 适配随机策略。由于策略梯度算法是基于策略函数的,因此可以适配随机策略,而基于价值的算法则需要一个确定的策略。此外其计算出来的策略梯度是无偏的,而基于价值的算法则是有偏的。
策略梯度算法缺点
- 采样效率低。由于使用的是蒙特卡洛估计,与基于价值算法的时序差分估计相比其采样速度必然是要慢很多的,这个问题在前面相关章节中也提到过。
- 高方差。虽然跟基于价值的算法一样都会导致高方差,但是策略梯度算法通常是在估计梯度时蒙特卡洛采样引起的高方差,这样的方差甚至比基于价值的算法还要高。
- 收敛性差。容易陷入局部最优,策略梯度方法并不保证全局最优解,因为它们可能会陷入局部最优点。策略空间可能非常复杂,存在多个局部最优点,因此算法可能会在局部最优点附近停滞。
- 难以处理高维离散动作空间:对于离散动作空间,采样的效率可能会受到限制,因为对每个动作的采样都需要计算一次策略。当动作空间非常大时,这可能会导致计算成本的急剧增加。
- 马尔可夫平稳分布需要满足什么条件?
- 非周期性:由于马尔可夫链需要收敛,那么就一定不能是周期性的,实际上我们处理的问题基本上都是非周期性的,这点不需要做过多的考虑。
- 状态连通性:即存在概率转移矩阵P,能够使得任意状态S0经过有限次转移到达状态s,反之亦然。
- REINFORCE 算法会比 Q-learning 算法训练速度更快吗?为什么?
是的。REINFORCE 算法直接优化一个参数化的策略函数,而不需要估计一个值函数.Q-learning 算法是一种基于价值的算法,它通过学习一个状态-动作值函数来评估不同动作的优劣,然后根据这个函数来选择最优的动作。
- 确定性策略与随机性策略的区别?
- 确定性策略是指在每个状态下,只选择一个固定的动作,不考虑其他可能的动作。确定性策略可以用一个函数来表示,即 a = μ ( s ) a = \mu(s) a=μ(s) ,其中 a 是动作,s 是状态, μ \mu μ是策略函数。
- 随机性策略是指在每个状态下,按照一定的概率分布来选择动作,而不是唯一确定的。随机性策略可以用一个条件概率来表示,即 π ( a ∣ s ) \pi(a|s) π(a∣s),其中 π \pi π是策略函数,表示在状态 s 下选择动作 a 的概率。
随机性策略可以更好地探索环境,避免陷入局部最优,而确定性策略可以更高效地利用已知的信息,减少计算量。
Actor-Ctitic算法
策略梯度算法优缺点:
- 适配连续动作空间。在将策略函数设计的时候我们已经展开过,这里不再赘述。
- 适配随机策略。由于策略梯度算法是基于策略函数的,因此可以适配随机策略,而基于价值的算法则需要一个确定的策略。此外其计算出来的策略梯度是无偏的,而基于价值的算法则是有偏的。
但同样的,策略梯度算法也有其缺点。
- 采样效率低。由于使用的是蒙特卡洛估计,与基于价值算法的时序差分估计相比其采样速度必然是要慢很多的,这个问题在前面相关章节中也提到过。
- 高方差。虽然跟基于价值的算法一样都会导致高方差,但是策略梯度算法通常是在估计梯度时蒙特卡洛采样引起的高方差,这样的方差甚至比基于价值的算法还要高。
- 收敛性差。容易陷入局部最优,策略梯度方法并不保证全局最优解,因为它们可能会陷入局部最优点。策略空间可能非常复杂,存在多个局部最优点,因此算法可能会在局部最优点附近停滞。
- 难以处理高维离散动作空间:对于离散动作空间,采样的效率可能会受到限制,因为对每个动作的采样都需要计算一次策略。当动作空间非常大时,这可能会导致计算成本的急剧增加。
结合策略梯度与值函数的Actor-Critic算法能够同时兼顾两者的优点,甚至还能缓解两种方法都很难解决的高方差问题。
策略梯度算法高方差来源为 直接对策略参数化,相当于既要利用策略与环境进行交互采样,又要利用采样去估计策略梯度。
价值函数算法高方差来源为 需要与环境交互采样来估计值函数。
而两者结合后,Actor网络部分还是负责估计策略梯度和采样,但是Critic网络 也就是原来的值函数部分就不需要采样只负责估计值函数,并且由于它估计的值函数为策略函数的只,相当于带来了一个更稳定的估计用于指导Actor的更新,反而能够缓解策略梯度估计带来的高方差。
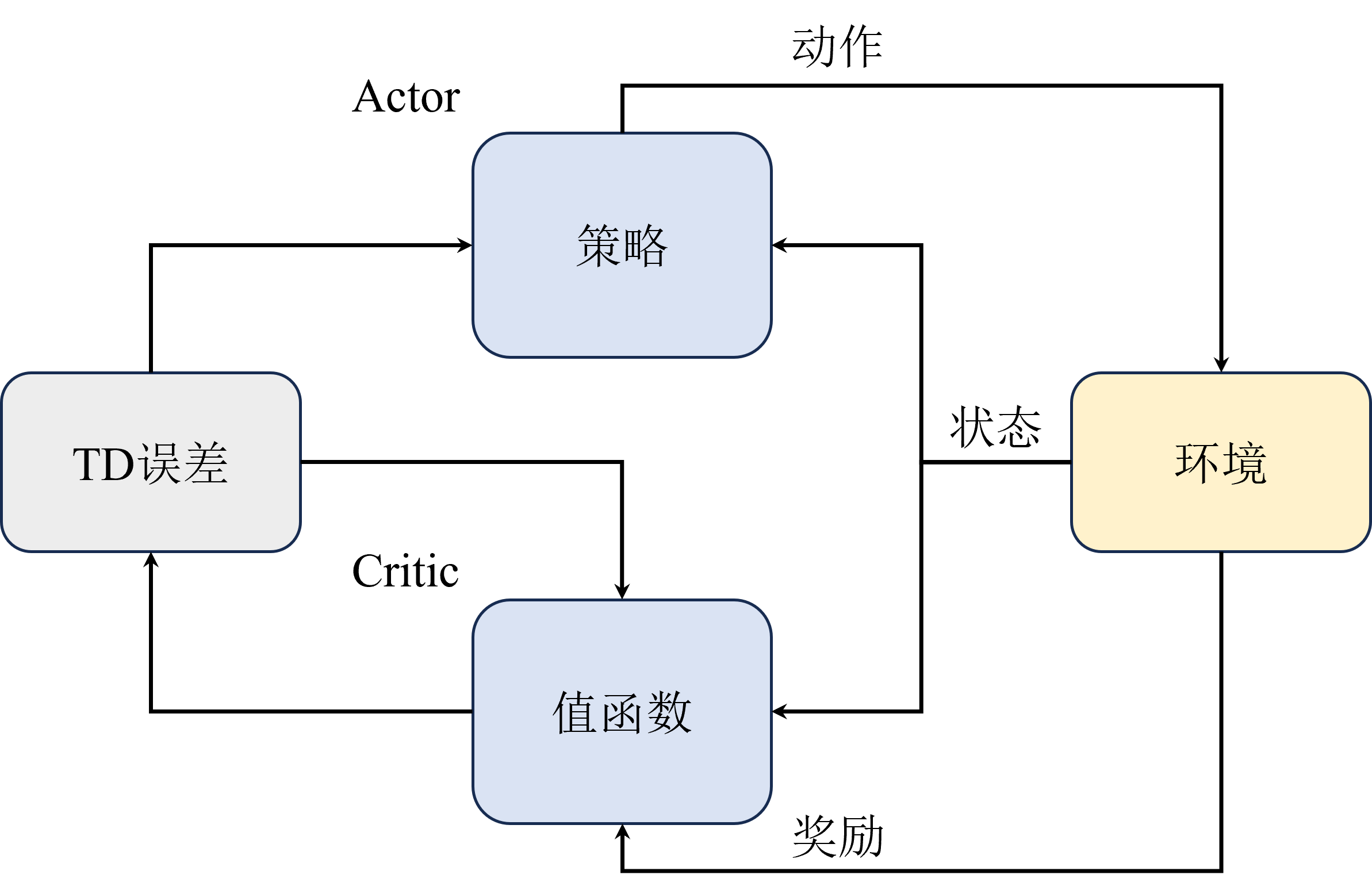
由于AC网络并不能彻底解决策略梯度算法的高方差问题,所以为了进一步缓解高方差问题,引入了一个优势函数,用来表示当前状态-动作对相当于平均水平的优势
KaTeX parse error: \tag works only in display equations
这里优势函数相当于减去了一个基线,可以自由选择,但是通常选择状态价值函数使得梯度估计更加稳定。即A2C算法。而A3C算法是在A2C基础上引入了多线程的概念提高训练效率。原先的 A2C 算法相当于只有一个全局网络并持续与环境交互更新。而 A3C 算法中增加了多个进程,每一个进程都拥有一个独立的网络和环境以供交互,并且每个进程每隔一段时间都会将自己的参数同步到全局网络中,这样就能提高训练效率。
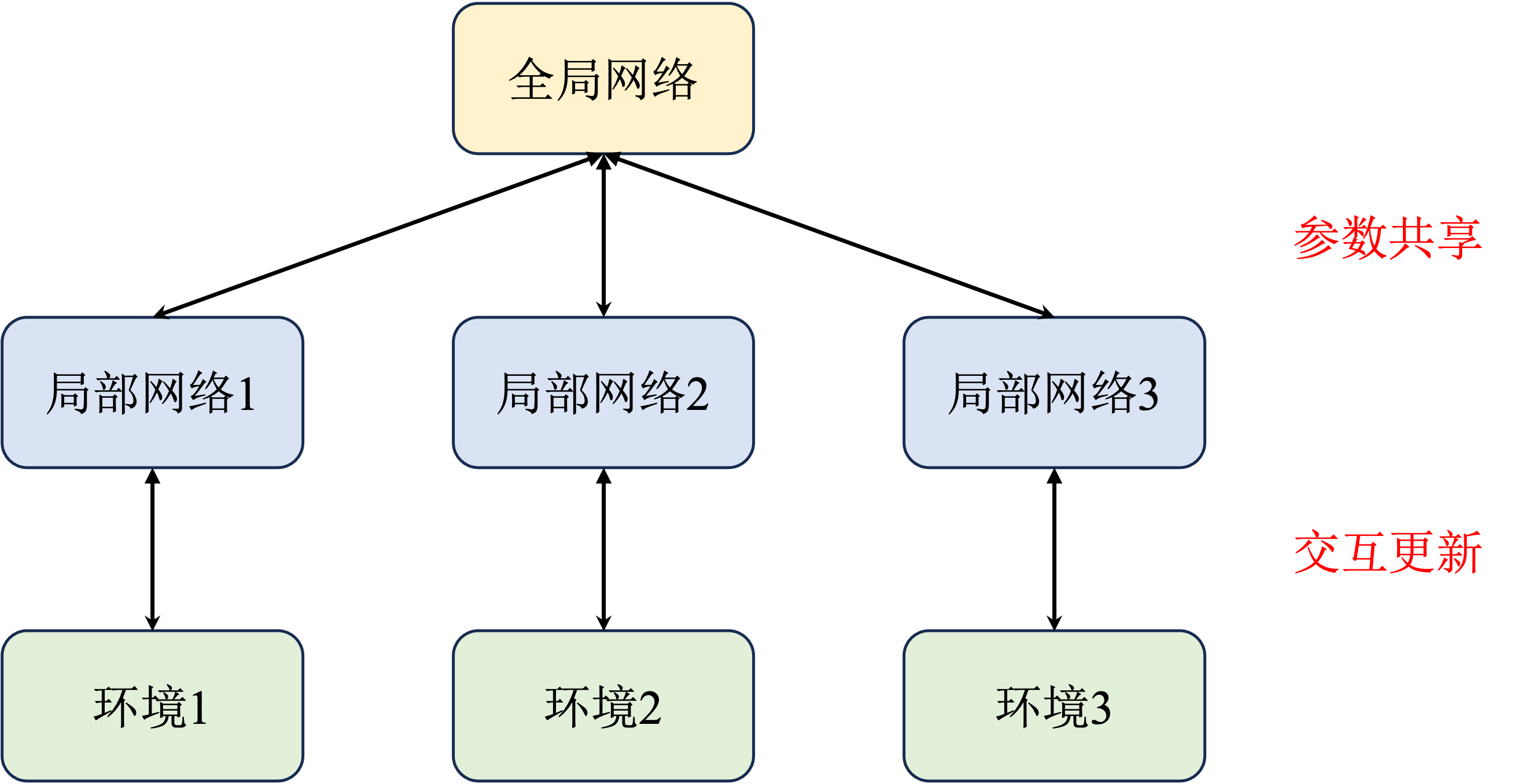
作业题
- 相比于 REINFORCE 算法, A2C 主要的改进点在哪里,为什么能提高速度?
A2C引入了优势函数与AC演员评论家网络。A2C 算法是一种演员-评论家算法,它引入了一个值函数作为评论家,可以在每一步或者每几步就根据优势函数来更新策略和值函数。可以衡量一个动作相对于平均水平的优劣。这些改进使得 A2C 算法能够更快地收敛到最优策略,提高了训练的速度和效果。
- A2C 算法是 on-policy 的吗?为什么?
什么能提高速度?
A2C引入了优势函数与AC演员评论家网络。A2C 算法是一种演员-评论家算法,它引入了一个值函数作为评论家,可以在每一步或者每几步就根据优势函数来更新策略和值函数。可以衡量一个动作相对于平均水平的优劣。这些改进使得 A2C 算法能够更快地收敛到最优策略,提高了训练的速度和效果。
- A2C 算法是 on-policy 的吗?为什么?
是的。 A2C 算法的目标是最大化累积回报的期望,而这个期望是基于当前的策略分布的,如果使用不同的策略分布来采样数据,那么就会导致偏差和不一致。
相关文章:

策略算法与Actor-Critic网络
策略算法 教程链接 DataWhale强化学习课程JoyRL https://johnjim0816.com/joyrl-book/#/ch7/main 策略梯度 与前面的基于价值的算法不同,这类算法直接对策略本身进行近似优化。 在这种情况下,我们可以将策略描述成一个带有参数 θ θ θ的连续函数…...

基于Pytest+Requests+Allure实现接口自动化测试
一、整体结构 框架组成:pytestrequestsallure 设计模式: 关键字驱动 项目结构: 工具层:api_keyword/ 参数层:params/ 用例层:case/ 数据驱动:data_driver/ 数据层:data/ 逻…...

【中间件】消息队列中间件intro
中间件middleware 内容管理 introwhy use MQMQ实现漫谈主流消息队列QMQ IntroQMQ架构QMQ 存储模型 本文还是从理论层面分析消息队列中间件 cfeng现在处于理论分析阶段,以中间件例子,之前的blog对于中间件是从使用角度分享了相关的用法,现在就…...
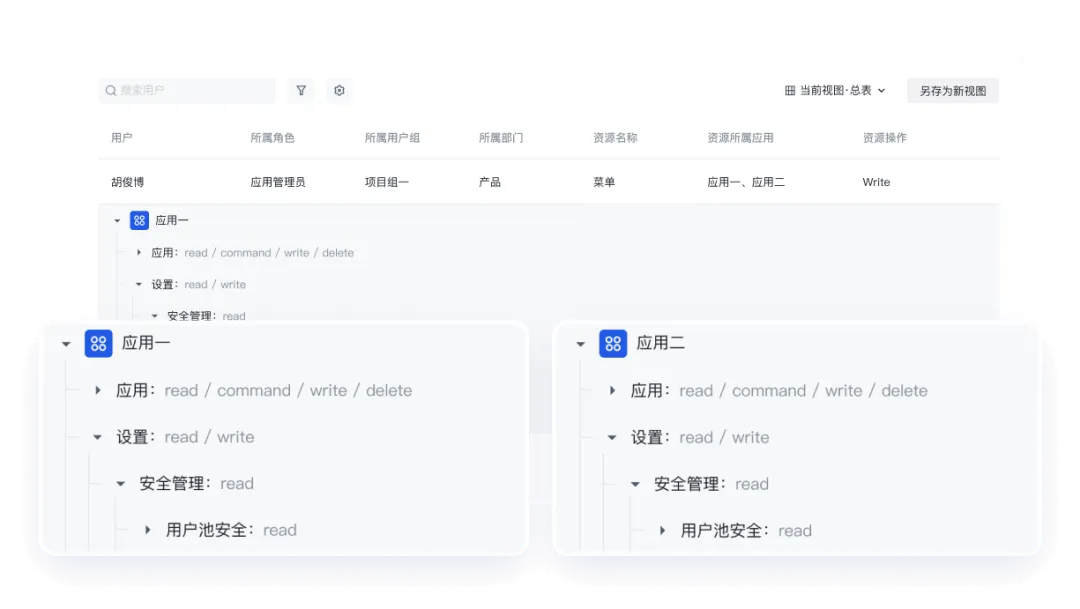
从 RBAC 到 NGAC ,企业如何实现自动化权限管理?
随着各领域加快向数字化、移动化、互联网化的发展,企业信息环境变得庞大复杂,身份和权限管理面临巨大的挑战。为了满足身份管理法规要求并管理风险,企业必须清点、分析和管理用户的访问权限。如今,越来越多的员工采用移动设备进行…...

vue3中如何使用TypeScript?
在Vue 3中引入和使用TypeScript非常简单。下面是在Vue 3中引入和使用TypeScript的步骤: 创建Vue 3项目:首先,使用Vue CLI创建一个新的Vue 3项目。可以使用以下命令: vue create my-project在创建项目时,选择TypeScri…...

Git基础操作:合并某个分支的一个目录到另一个分支
有的时候不小心在错误的分支A上开发了一点代码,也已经提交了;或者分支A原计划先上线的,但是业务调整需要插一个需求进来,但是插进来的需求中有一部分代码在分支A中已经写过了。 这个时候如果想把这部分代码移到正确的分支B上可以…...

学习grdecl文件格式
一、初步了解 最近在学习grdecl文件格式,文档不多。查找资料发现,这个格式的文件是由斯伦贝谢公司的ECLIPSE专业软件生成的。 搜到一些文档,都是2010年之前的,似乎有些用处。文档也交代了这个文件格式分为二进制和文本格式…...
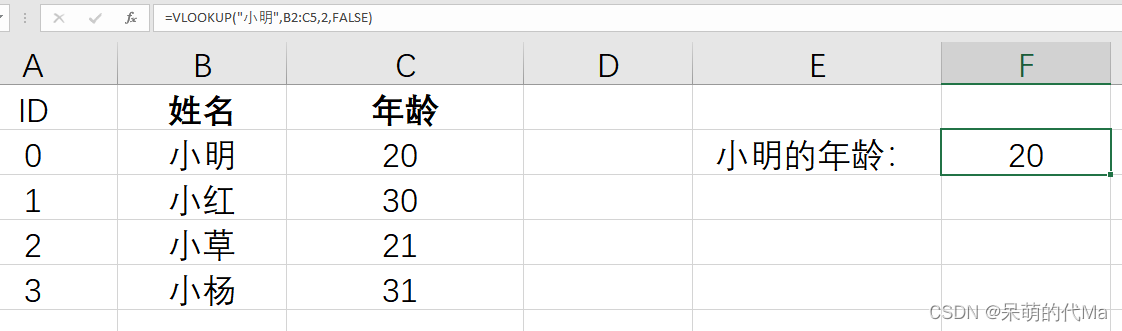
Excel使用VLOOKUP查询数据
VLOOKUP函数在百度百科中的解释是: 解释一下,函数需要4个参数: 参数1(lookup_value):需要匹配的值参数2(table_array):在哪个区域里进行匹配参数3(col_index…...

SpectralGPT: Spectral Foundation Model 论文翻译2
遥感领域的通用大模型 2023.11.13在CVPR发表 原文地址:[2311.07113] SpectralGPT: Spectral Foundation Model (arxiv.org) 实验 在本节中,我们将严格评估我们的SpectralGPT模型的性能,并对其进行基准测试SOTA基础模型:ResN…...

Java编译过程中的JVM
流程 源代码编写: 首先,开发者使用Java编程语言编写源代码。这些源代码通常保存在扩展名为.java的文件中。 编译源代码: 使用Java编译器(例如javac),这些.java文件被编译成Java字节码。字节码是一种中间形…...
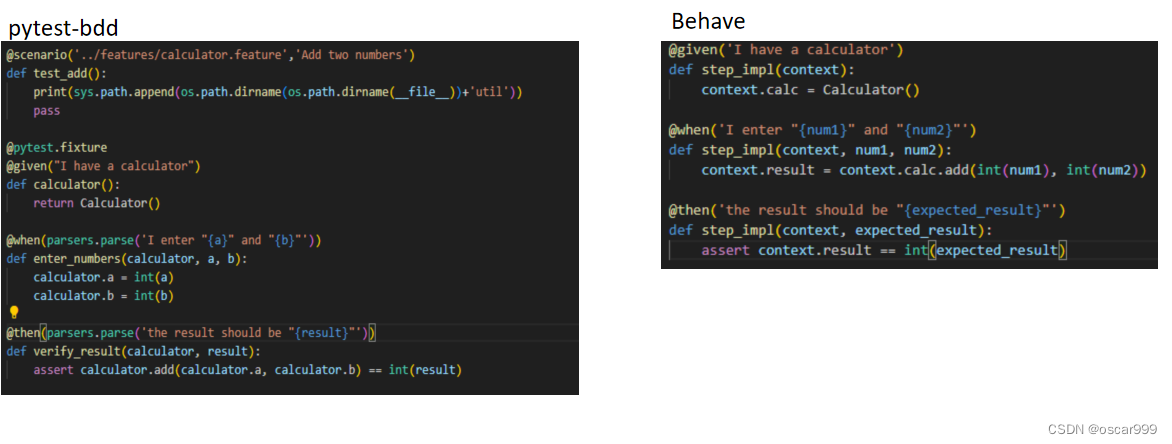
Python BDD 框架比较之 pytest-bdd vs behave
pytest-bdd和behave是 Python 的两个流行的 BDD 测试框架,两者都可以用来编写用户故事和可执行的测试用例, 具体选择哪一个则需要根据实际的项目状况来看。 先简单看一下两者的功能: pytest-bdd 基于pytest测试框架,可以与pytest…...
)
【面经八股】搜广推方向:常见面试题(一)
【面经&八股】搜广推方向:常见面试题(一) 文章目录 【面经&八股】搜广推方向:常见面试题(一)1. 线下效果提升、线上效果不好。2. XGBoost 和 GBDT是什么?有什么区别?3. 偏差与方差。延伸知识(集成学习的三种方式: Bagging、Boosting、Stacking)。4. 随机森林…...
斐讯K2结合Padavan实现锐捷认证破解方法
前言 众所周知,校园网在传统模式下是不能直接插路由使用的,但苦于校园网只能连接一台设备的烦恼,不得不“另辟蹊径”来寻求新的解决路径,这不,它来了,它来了,它带着希望走来了。 本文基于斐讯…...
SpringBoot : ch06 整合 web (一)
前言 SpringBoot作为一款优秀的框架,不仅提供了快速开发的能力,同时也提供了丰富的文档和示例,让开发者更加容易上手。在本博客中,我们将介绍如何使用SpringBoot来整合Web应用程序的相关技术,并通过实例代码来演示如何…...

C++:OJ练习(每日练习系列)
编程题: 题一:把字符串转换成整数 把字符串转换成整数_牛客题霸_牛客网 示例1 输入: "2147483647" 返回值: 2147483647思路一: 第一步:it从str的第一个字符开始遍历,定义一个最后输…...
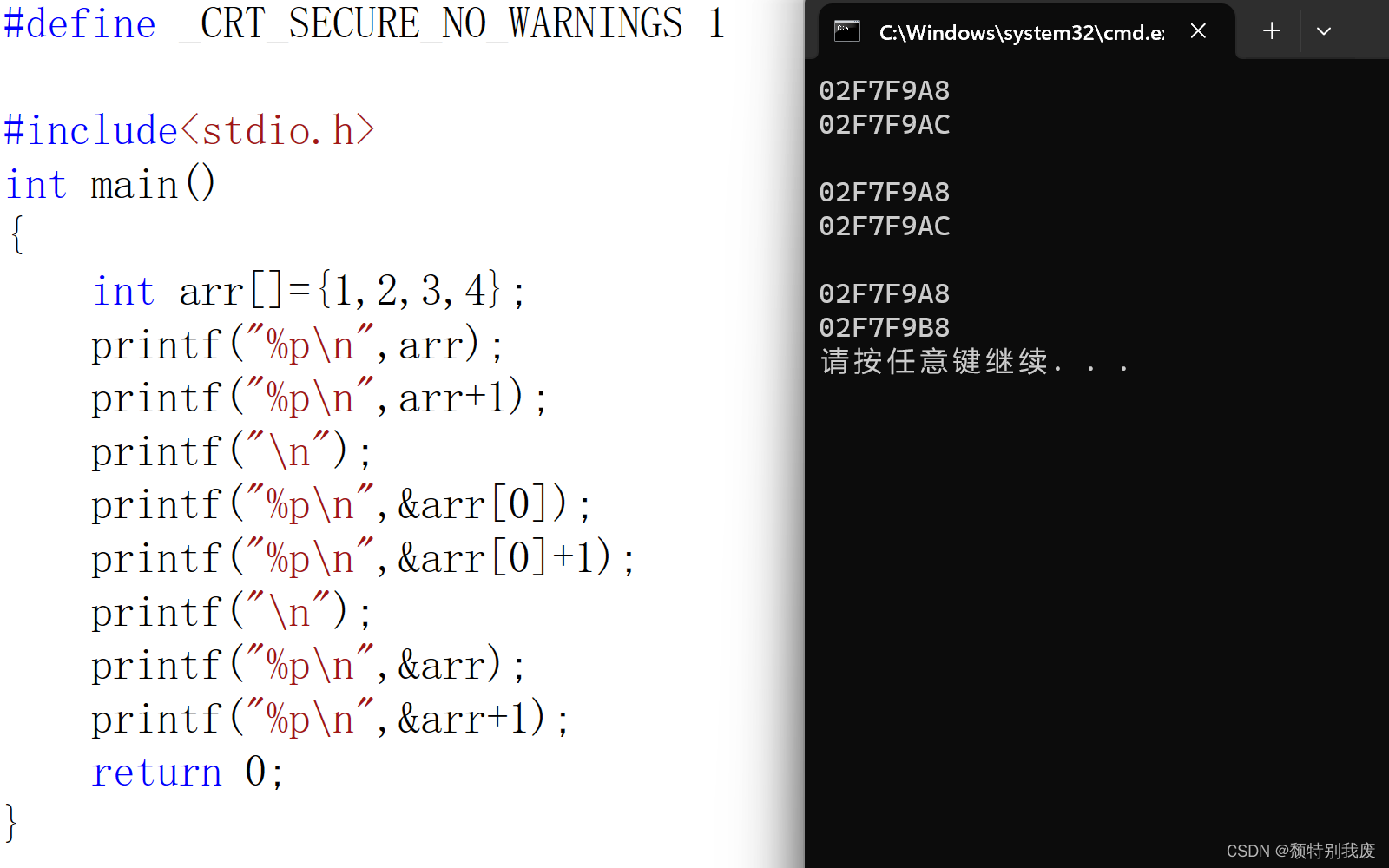
C语言—什么是数组名
#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h> int main() {int arr[]{1,2,3,4};printf("%p\n",arr);printf("%p\n",&arr);printf("%p\n",*arr);return 0; } 结论:数组名是数组首元素地址(下标为0的元素…...

如何与死锁斗争!!!
其他系列文章导航 Java基础合集 设计模式合集 多线程合集 分布式合集 ES合集 文章目录 其他系列文章导航 文章目录 前言 一、死锁场景现场 二、死锁是如何产生的 三、死锁排查思路 四、sql模拟死锁复现 五、死锁的解决方案 前言 为避免影响业务,应尽可能避…...
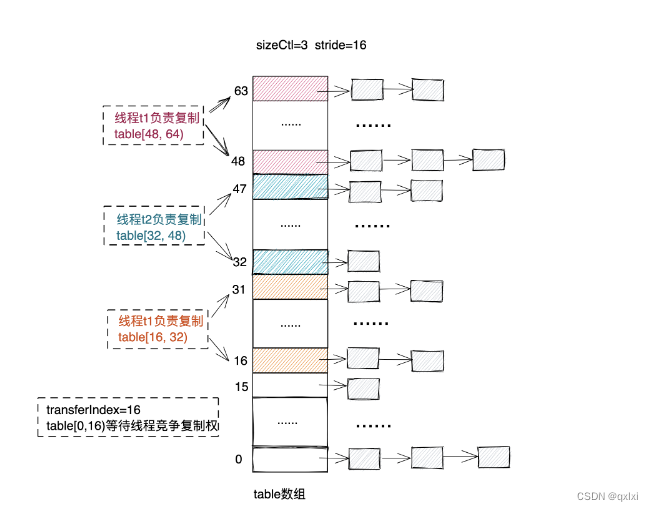
【Java并发】聊聊不安全的HashMap以及ConcurrentHashMap
在实际的开发中,hashmap是比较常用的数据结构,如果所开发的系统并发量不高,那么没有问题,但是一旦系统的并发量增加一倍,那么就可能出现不可控的系统问题,所以在平时的开发中,我们除了需要考虑正…...
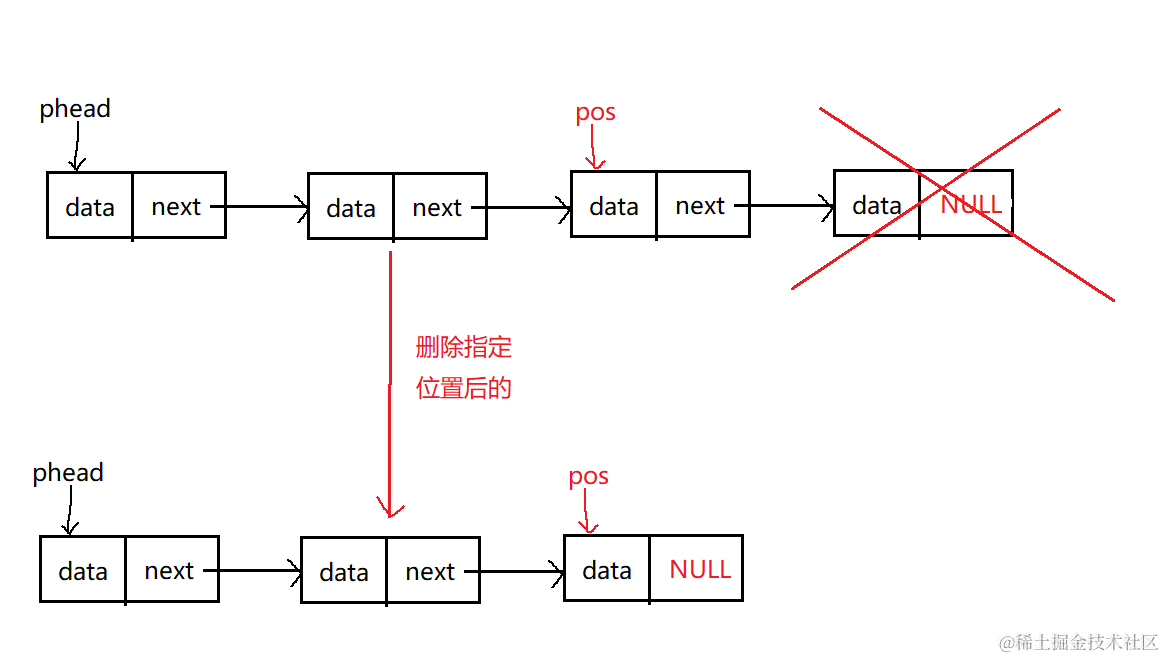
数据结构--->单链表
文章目录 链表链表的分类 单链表单链表的存储结构单链表主要实现的接口函数单链表尾插动态申请新节点单链表头插单链表的尾删单链表的头删在指定位置之前插入单链表查找插入 在指定位置之后插删除指定位置元素删除指定位置之后的元素顺序输出链表销毁单链表 顺序表和单链表的区…...

RT-Thread 线程间同步【信号量、互斥量、事件集】
线程间同步 一、信号量1. 创建信号量2. 获取信号量3. 释放信号量4. 删除信号量5. 代码示例 二、互斥量1. 创建互斥量2. 获取互斥量3. 释放互斥量4. 删除互斥量5. 代码示例 三、事件集1. 创建事件集2. 发送事件3. 接收事件4. 删除事件集5. 代码示例 简单来说,同步就是…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...
