C语言—什么是数组名
#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h>
int main()
{int arr[]={1,2,3,4};printf("%p\n",arr);printf("%p\n",&arr);printf("%p\n",*arr);return 0;
}
结论:数组名是数组首元素地址(下标为0的元素是首元素)
例外:
1、sizeof(数组名),该数组数组名表示整个数组,sizeof计算数组大小,单位字节
#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h>
int main()
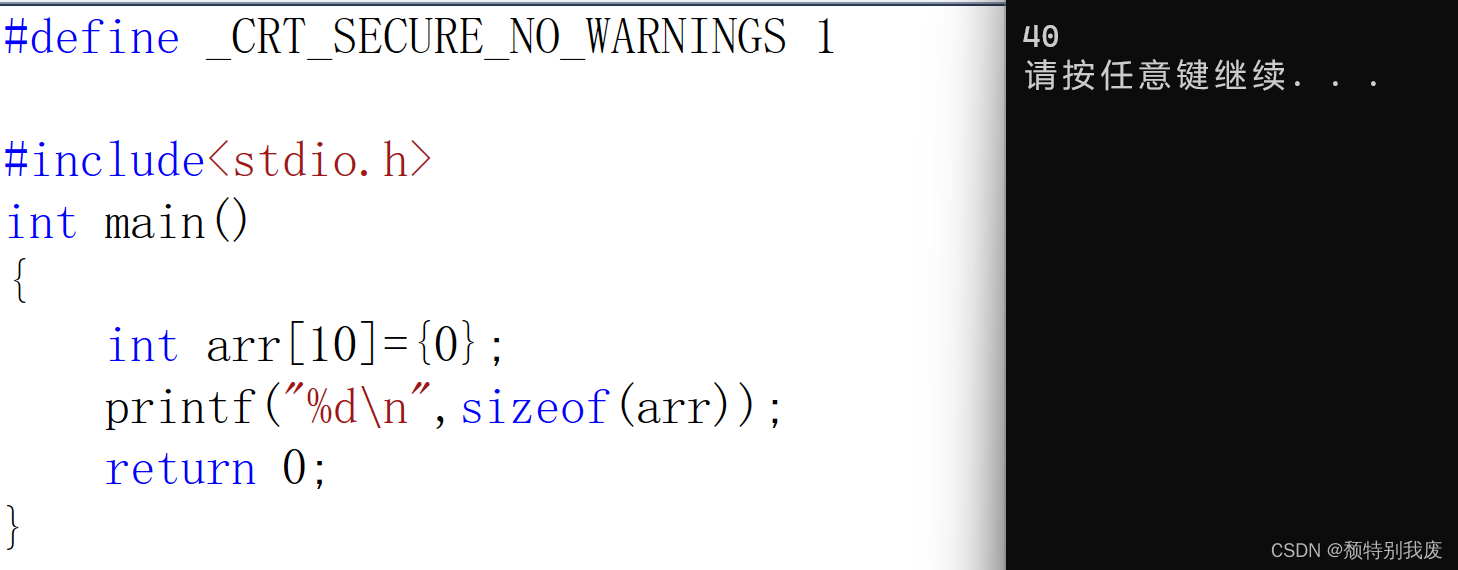
{int arr[10]={0};printf("%d\n",sizeof(arr));return 0;
}
2、&(数组名),数组名代表整个数组,取出的是整个数组的地址
#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h>
int main()
{int arr[]={1,2,3,4};printf("%p\n",arr);printf("%p\n",&arr[0]);printf("%p\n",&arr);return 0;
}
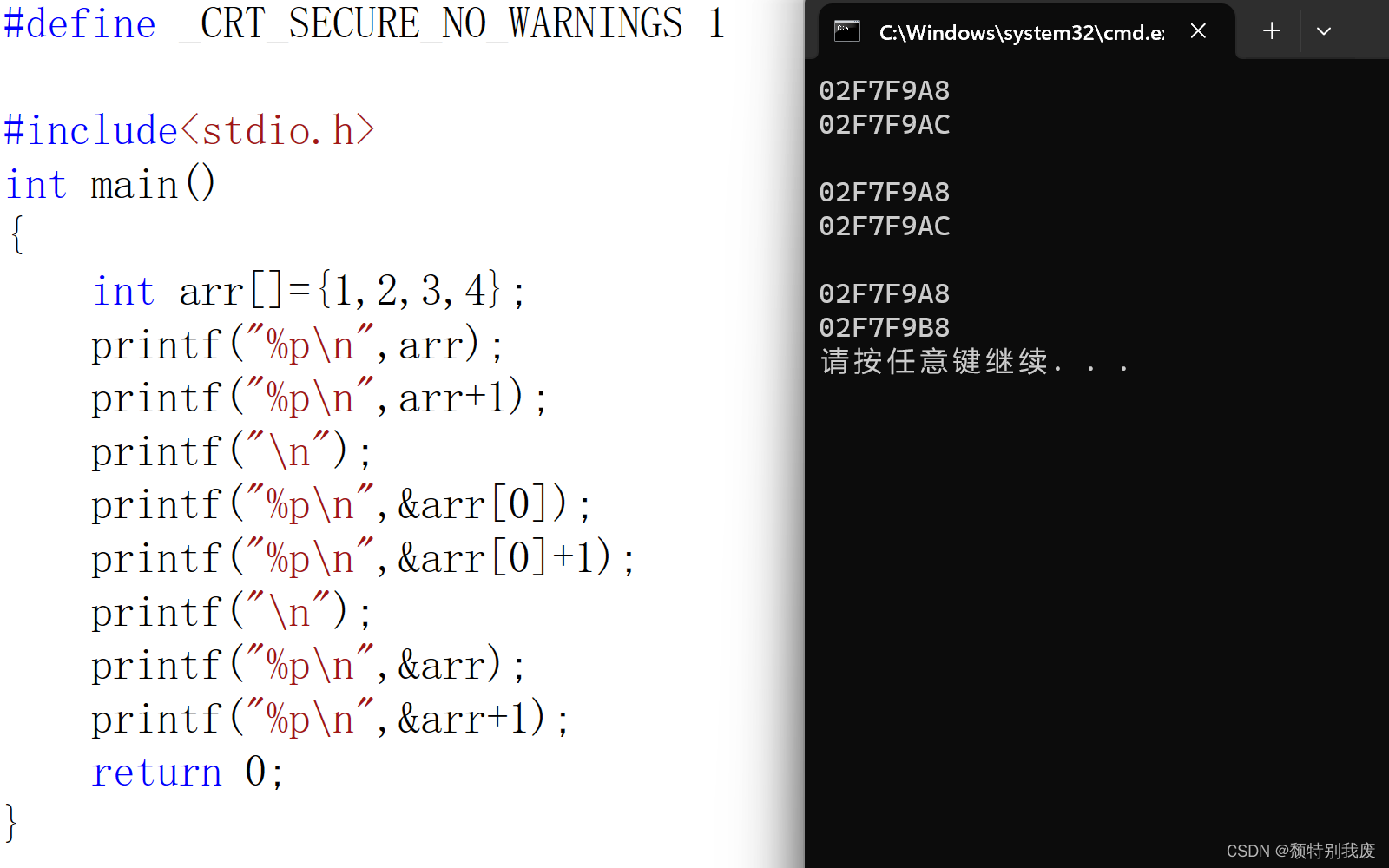
输出的结果是一样的,但是&(arr)的地址代表的是从第一个数组元素开始,分别+1发现输出结果不通,因为&arr+1输出的是数组的地址,而其他输出的是数组中首元素+1的元素地址(第二个元素地址)
#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h>
int main()
{int arr[]={1,2,3,4};printf("%p\n",arr);printf("%p\n",arr+1);printf("\n");printf("%p\n",&arr[0]);printf("%p\n",&arr[0]+1);printf("\n");printf("%p\n",&arr);printf("%p\n",&arr+1);return 0;
} 
相关文章:

C语言—什么是数组名
#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h> int main() {int arr[]{1,2,3,4};printf("%p\n",arr);printf("%p\n",&arr);printf("%p\n",*arr);return 0; } 结论:数组名是数组首元素地址(下标为0的元素…...

如何与死锁斗争!!!
其他系列文章导航 Java基础合集 设计模式合集 多线程合集 分布式合集 ES合集 文章目录 其他系列文章导航 文章目录 前言 一、死锁场景现场 二、死锁是如何产生的 三、死锁排查思路 四、sql模拟死锁复现 五、死锁的解决方案 前言 为避免影响业务,应尽可能避…...
【Java并发】聊聊不安全的HashMap以及ConcurrentHashMap
在实际的开发中,hashmap是比较常用的数据结构,如果所开发的系统并发量不高,那么没有问题,但是一旦系统的并发量增加一倍,那么就可能出现不可控的系统问题,所以在平时的开发中,我们除了需要考虑正…...
数据结构--->单链表
文章目录 链表链表的分类 单链表单链表的存储结构单链表主要实现的接口函数单链表尾插动态申请新节点单链表头插单链表的尾删单链表的头删在指定位置之前插入单链表查找插入 在指定位置之后插删除指定位置元素删除指定位置之后的元素顺序输出链表销毁单链表 顺序表和单链表的区…...

RT-Thread 线程间同步【信号量、互斥量、事件集】
线程间同步 一、信号量1. 创建信号量2. 获取信号量3. 释放信号量4. 删除信号量5. 代码示例 二、互斥量1. 创建互斥量2. 获取互斥量3. 释放互斥量4. 删除互斥量5. 代码示例 三、事件集1. 创建事件集2. 发送事件3. 接收事件4. 删除事件集5. 代码示例 简单来说,同步就是…...
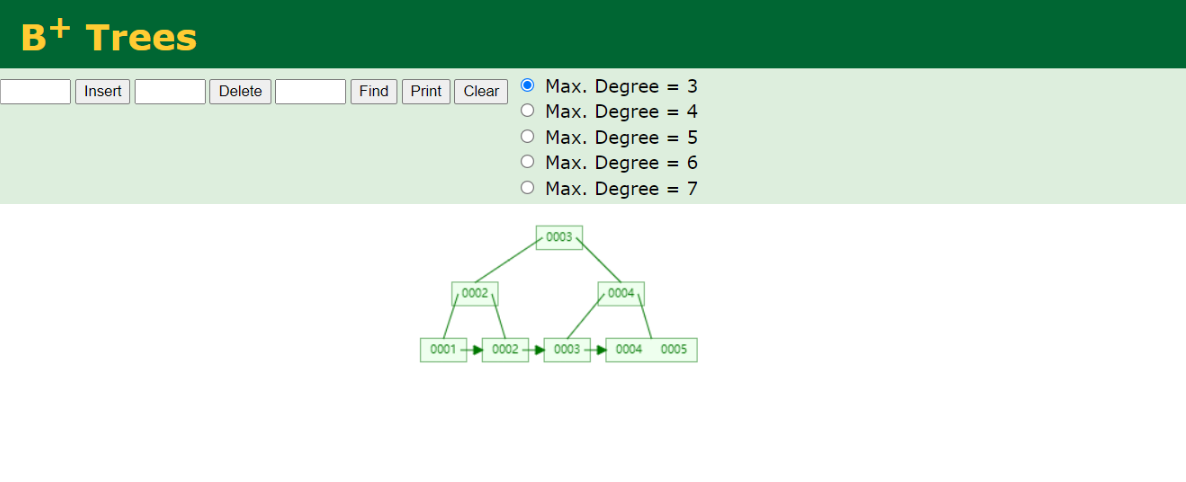
B 树和 B+树 的区别
文章目录 B 树和 B树 的区别 B 树和 B树 的区别 了解二叉树、AVL 树、B 树的概念 B 树和 B树的应用场景 B 树是一种多路平衡查找树,为了更形象的理解。 二叉树,每个节点支持两个分支的树结构,相比于单向链表,多了一个分支。 …...

Go iota简介
当声明枚举类型或定义一组相关常量时,Go语言中的iota关键字可以帮助我们简化代码并自动生成递增的值。本文档将详细介绍iota的用法和行为。 iota关键字 iota是Go语言中的一个预定义标识符,它用于创建自增的无类型整数常量。iota的行为类似于一个计数器…...
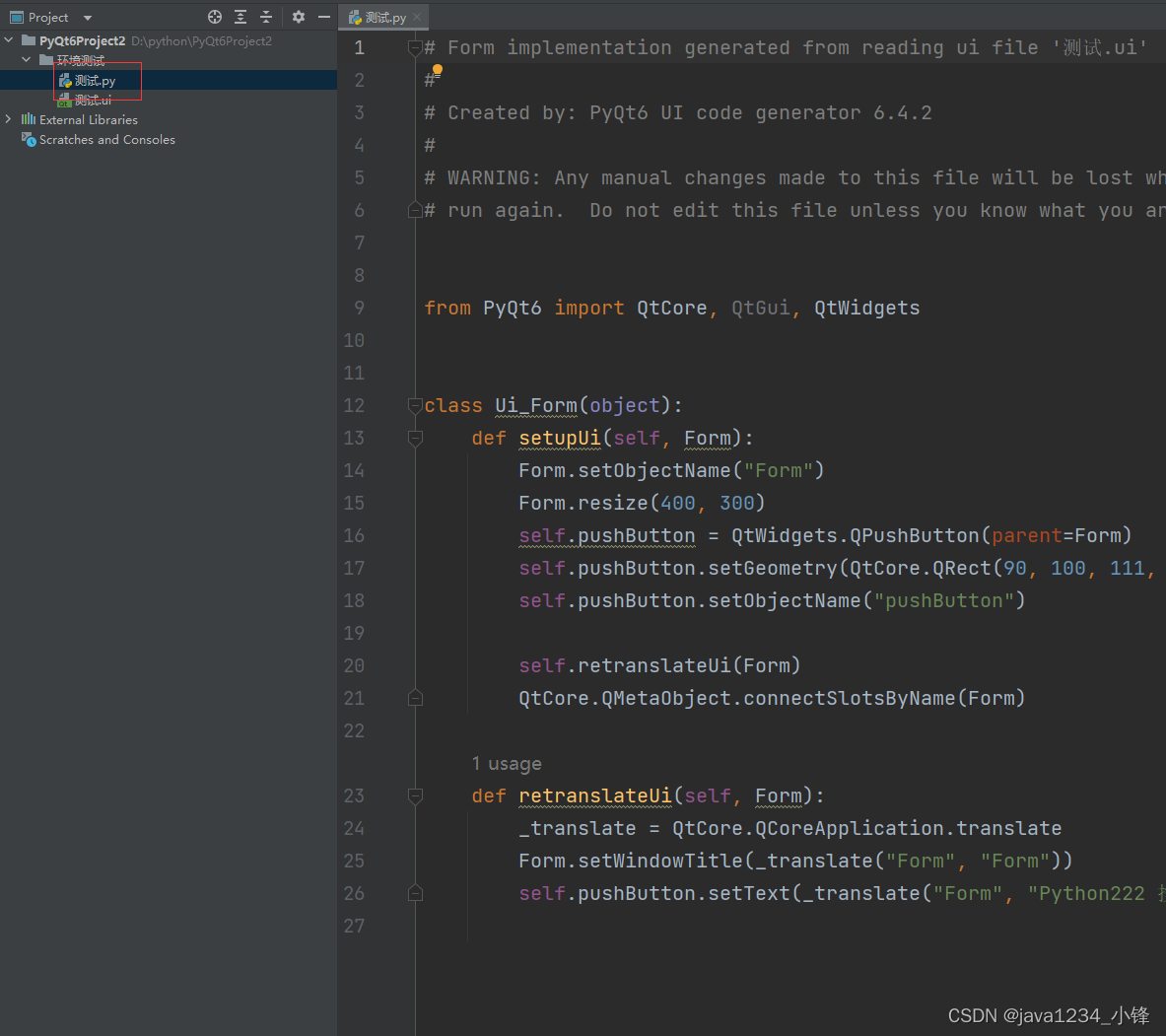
PyQt6库和工具库QTDesigner安装与配置
锋哥原创的PyQt6视频教程: 2024版 PyQt6 Python桌面开发 视频教程(无废话版) 玩命更新中~_哔哩哔哩_bilibili2024版 PyQt6 Python桌面开发 视频教程(无废话版) 玩命更新中~共计12条视频,包括:2024版 PyQt6 Python桌面开发 视频教程(无废话版…...

性能测试:系统架构性能优化思路
今天谈下业务系统性能问题分析诊断和性能优化方面的内容。这篇文章重点还是谈已经上线的业务系统后续出现性能问题后的问题诊断和优化重点。 系统性能问题分析流程 我们首先来分析下如果一个业务系统上线前没有性能问题,而在上线后出现了比较严重的性能问题&#x…...

python字符串格式化
字符串格式化 # 2023年11月16日 星期四 y 2023 m 11 d 16 w 四 s %d年%d月%d日 星期%s%(y,m,d,w) print(s) s {}年{}月{}日 星期{}.format(y,m,d,w) print(s) s f{y}年{m}月{d}日 星期{w} print(s)...
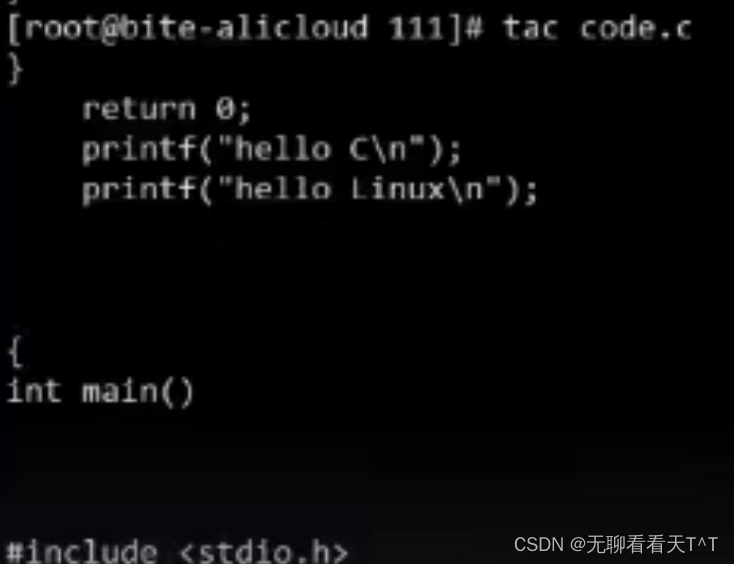
Linux的基本指令(二)
目录 前言 学前补充 touch指令 mkdir指令 rmdir指令 rm指令 通配符* man指令 cp指令 mv指令(重要) 补充内容: 1、如何快速在Linux中写出代码 2、如何看待如此多的Linux指令 cat指令 前言 关于Linux的基本指令我们会分三到四篇文章进行分析,…...
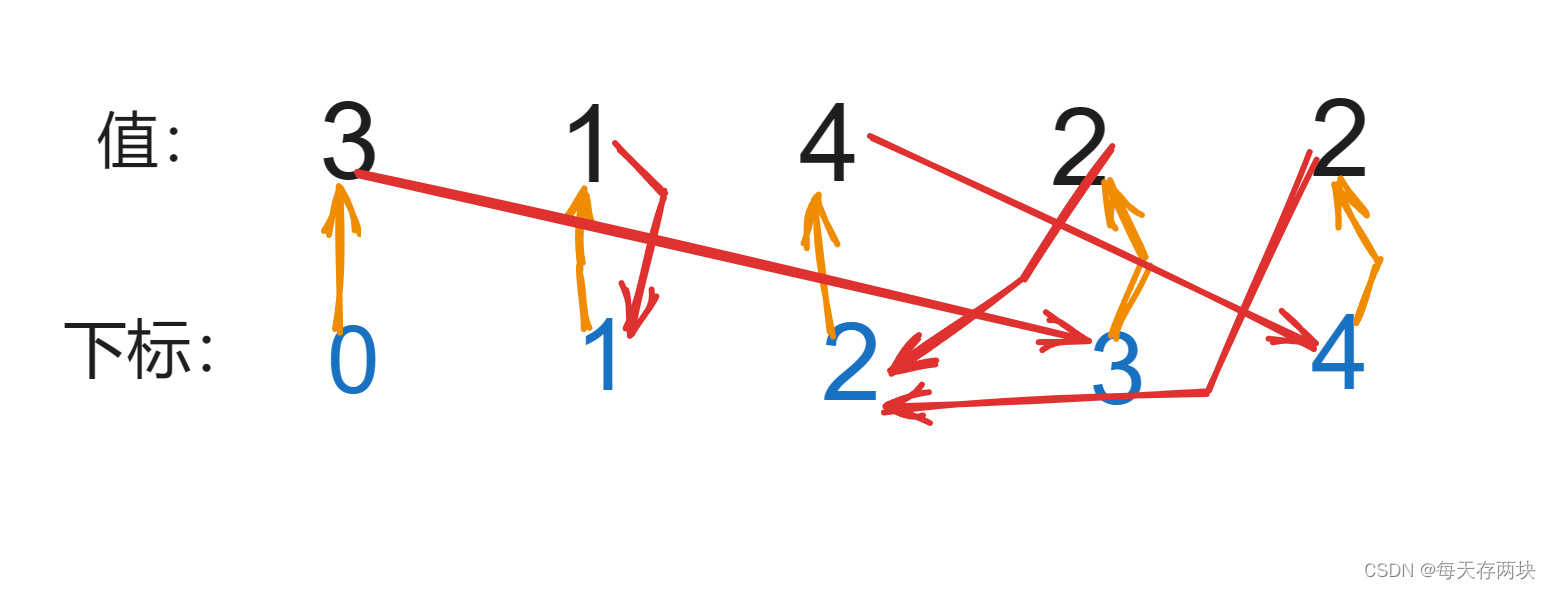
每日一题--寻找重复数
蝶恋花-王国维 阅尽天涯离别苦, 不道归来,零落花如许。 花底相看无一语,绿窗春与天俱莫。 待把相思灯下诉, 一缕新欢,旧恨千千缕。 最是人间留不住,朱颜辞镜花辞树。 目录 题目描述: 思路分析…...
C#,《小白学程序》第二十二课:大数的乘法(BigInteger Multiply)
1 文本格式 using System; using System.Linq; using System.Text; using System.Collections.Generic; /// <summary> /// 大数的(加减乘除)四则运算、阶乘运算 /// 乘法计算包括小学生算法、Karatsuba和Toom-Cook3算法 /// </summary> p…...
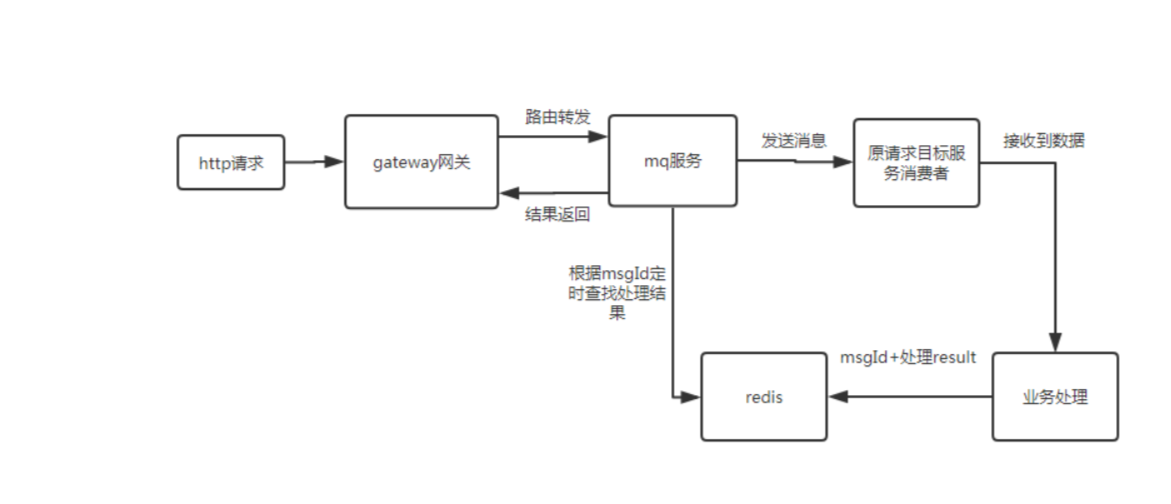
kafka,RabbitMQ,RocketMQ,他们之间的区别,架构,如何保证消息的不丢失,保证不重复消费,保证消息的有序性
文章目录 Kafka、RabbitMQ、RocketMQ 之间的区别是什么?性能数据可靠性服务可用性功能 RabbitMQ如何保证消息不丢失?Kafka 的架构说一下?Kafka 怎么保证消息是有序的?Kafka 怎么解决重复消费?Kafka 怎么保证消息不丢失…...

uni-app中vue3+setup实现下拉刷新、上拉加载更多效果
在小程序或各类app中,下拉刷新和上拉加载更多是极为常见和使用非常频繁的两个功能,通过对这两个功能的合理使用可以极大的方便用户进行操作。 合理的设计逻辑才能更容易挽留住用户,因为这些细节性的小功能点就变得极为重要起来。 那么在uni…...

微服务实战系列之Nginx(技巧篇)
前言 今天北京早晨竟然飘了一些“雪花”,定睛一看,似雪非雪,像泡沫球一样,原来那叫“霰”。 自然中,雨雪霜露雾,因为出场太频繁,认识门槛较低,自然不费吹灰之力,即可享受…...

好工具|datamap,一个好用的地图可视化Excel插件,在Excel中实现地理编码、拾取坐标
在做VRP相关研究的时候,需要对地图数据做很多处理,比如地理编码,根据“重庆市沙坪坝区沙正街174号”这样的一个文本地址知道他的经纬度;再比如绘制一些散点图,根据某个位置的经纬度在地图上把它标注出来。还有有的时候…...

Java——继承
继承是面向对象编程的三大特征之一,它让我们更加容易实现对已有类的扩展、更加容易实现对现实世界的建模。 继承有两个主要作用: 代码复用,更加容易实现类的扩展方便建模 继承的实现 继承让我们更加容易实现对类的扩展。比如我们定义了人…...

十、sdl显示yuv图片
前言 SDL中内置加载BMP的API,使用起来会更加简单,便于初学者学习使用SDL 如果需要加载JPG、PNG等其他格式的图片,可以使用第三方库:SDL_image 测试环境: ffmpeg的4.3.2自行编译版本windows环境qt5.12sdl2.0.22&…...

Docker Nginx容器部署vue项目
Docker Nginx容器部署vue项目 文章目录 Docker Nginx容器部署vue项目1. 前提2. 下载nginx镜像3. 编写nginx.conf配置文件4. 编写构建命令5. vue项目上传 1. 前提 Docker服务已部署 2. 下载nginx镜像 首先查看有没有nginx镜像 docker images没有的情况下再进行下载 docker …...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...
