前缀和与差分
文章目录
- 前缀和
- 一维前缀和
- 公式
- CODE
- 二维前缀和
- 公式
- CODE
- 差分
- 一维差分
- 思路
- 作用
- CODE
- 二维差分
- 思路
- CODE
前缀和
一维前缀和
板子题:https://www.acwing.com/activity/content/problem/content/829/
公式
S [ i ] = a [ i ] + S [ i − 1 ] S[i] = a[i] + S[i - 1] S[i]=a[i]+S[i−1]
CODE
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 1e5 + 10;
int n, m, l, r;
int a[N], s[N];int main()
{cin >> n >> m;for(int i = 1; i <= n; ++i){scanf("%d", &a[i]);s[i] = s[i - 1] + a[i];}while(m--){cin >> l >> r;printf("%d\n", s[r] - s[l - 1]);}
}
二维前缀和
板子题:https://www.acwing.com/activity/content/problem/content/830/
公式
S [ i ] [ j ] = S [ i − 1 ] [ j ] + S [ i ] [ j − 1 ] − S [ i − 1 ] [ j − 1 ] + a [ i ] [ j ] S[i][j] = S[i - 1][j] + S[i][j - 1] - S[i - 1][j - 1] + a[i][j] S[i][j]=S[i−1][j]+S[i][j−1]−S[i−1][j−1]+a[i][j]
CODE
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 1010;
int n, m, q;
int x1, x2, y1, y2;
int a[N][N], s[N][N];int main()
{cin >> n >> m >> q;for(int i = 1; i <= n; ++i)for(int j = 1; j <= m; ++j){scanf("%d", &a[i][j]);s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];}while (q -- ){cin >> x1 >> y1 >> x2 >> y2;printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);}
}
差分
一维差分
板子题:https://www.acwing.com/activity/content/problem/content/831/
思路
差分其实是前缀和的逆运算,我们假想有一个数组b[],它的前缀和是数组a[],也就是说:
b [ i ] = a [ i ] − a [ i − 1 ] b[i] = a[i] - a[i - 1] b[i]=a[i]−a[i−1]
作用
这个b[]数组有什么用呢?
在我们对a[]的元素进行加减操作时,如果采用遍历a[]的方法,时间是 o ( N ) o(N) o(N) 的,但是如果我们用b[]对其优化可以使时间复杂度降到 o ( 1 ) o(1) o(1)。
对a[]的 [ i , j ] [i, j] [i,j] 段进行+k操作,我们可以在 b[i] + k并在b[j + 1] - k。当我们对b[]求前缀和时,从i开始的每个元素都会+k,但是我们只要加到a[j]就结束了,所以在a[j + 1]进行归位。
CODE
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;const int N = 1e5 + 10;
int n, m;
int l, r, c;
int a[N], b[N];void insert(int l, int r, int c){b[l] += c;b[r + 1] -= c;
}int main()
{cin >> n >> m;for(int i = 1; i <= n; ++i){ scanf("%d", &a[i]);insert(i, i, a[i]);}while (m -- ){cin >> l >> r >> c;insert(l, r, c);}for(int i = 1; i <= n; ++i) printf("%d ", b[i] += b[i - 1]);
}
整个差分数组的精髓就在于insert()函数,非常巧妙啊,尤其是在读入阶段对b[]数组进行初始化时的操作,这个操作的意义如下:

来源:https://www.acwing.com/activity/content/code/content/39799/
二维差分
板子题:https://www.acwing.com/activity/content/problem/content/832/
思路
答题思路跟一维差分差不多,借鉴二维前缀和的操作我们可以得到以下公式:
a [ i ] [ j ] = b [ i ] [ j ] − b [ i − 1 ] [ j ] − b [ i ] [ j − 1 ] + b [ i − 1 ] [ j − 1 ] a[i][j] = b[i][j] - b[i - 1][j] - b[i][j - 1] + b[i - 1][j - 1] a[i][j]=b[i][j]−b[i−1][j]−b[i][j−1]+b[i−1][j−1]
那我们插入函数该怎么写呢?
一样的原理:
b [ x 1 ] [ y 1 ] + = c b [ x 2 + 1 ] [ y 1 ] − = c b [ x 1 ] [ y 2 + 1 ] − = c b [ x 2 + 1 ] [ y 2 + 1 ] + = c b[x1][y1] += c\\ b[x2 + 1][y1] -= c\\ b[x1][y2 + 1] -=c\\ b[x2 + 1][y2 + 1] += c b[x1][y1]+=cb[x2+1][y1]−=cb[x1][y2+1]−=cb[x2+1][y2+1]+=c
CODE
#include <iostream>
#include <cstring>
#include <algorithm>using namespace std;int n, m, q;
const int N = 1010;
int a[N][N], b[N][N];
int x1, y1, x2, y2, c;void insert(int x1, int y1, int x2, int y2, int c){b[x1][y1] += c;b[x2 + 1][y1] -= c;b[x1][y2 + 1] -= c;b[x2 + 1][y2 + 1] += c;
}int main()
{cin >> n >> m >> q;for(int i = 1; i <= n; ++i)for(int j = 1; j <= m; ++j){scanf("%d", &a[i][j]);insert(i, j, i, j, a[i][j]);}while(q--){cin >> x1 >> y1 >> x2 >> y2 >> c;insert(x1, y1, x2, y2, c);}for(int i = 1; i <= n; ++i){for(int j = 1; j <= m; ++j){printf("%d ", b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1]);}printf("\n"); }
}
相关文章:

前缀和与差分
文章目录 前缀和一维前缀和公式CODE 二维前缀和公式CODE 差分一维差分思路作用CODE 二维差分思路CODE 前缀和 一维前缀和 板子题:https://www.acwing.com/activity/content/problem/content/829/ 公式 S [ i ] a [ i ] S [ i − 1 ] S[i] a[i] S[i - 1] S[i]…...

力扣hot100 滑动窗口最大值 单调队列
👨🏫 题目地址 🍻 AC code class Solution {public int[] maxSlidingWindow(int[] nums, int k){int n nums.length;int[] res new int[n - k 1]; // 单调递减队列int[] q new int[n];// q数组维护的是元素在 nums 数组对应的下标int…...

mysql MHA配置文件
[rootlocalhost mastermha]# cat app1.cnf [server default]默认服务器配置 check_repl_delay0 #默认值为1,表示如果slave中从库落后主库relay log超过100M,主库不会选 择这个从库为新的master,因为这个从库进行恢复需要很长的时间.通过设置参数check_r…...
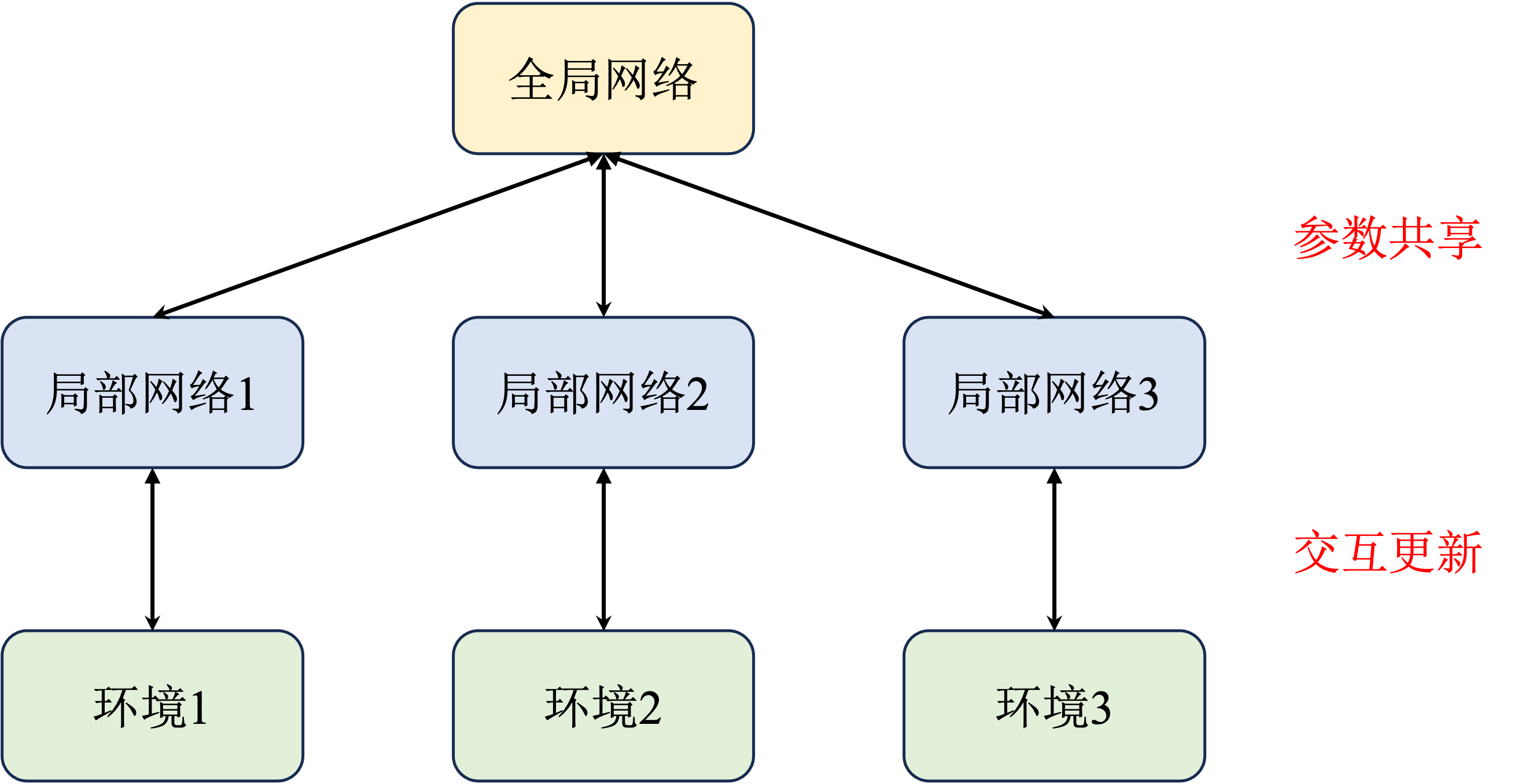
策略算法与Actor-Critic网络
策略算法 教程链接 DataWhale强化学习课程JoyRL https://johnjim0816.com/joyrl-book/#/ch7/main 策略梯度 与前面的基于价值的算法不同,这类算法直接对策略本身进行近似优化。 在这种情况下,我们可以将策略描述成一个带有参数 θ θ θ的连续函数…...

基于Pytest+Requests+Allure实现接口自动化测试
一、整体结构 框架组成:pytestrequestsallure 设计模式: 关键字驱动 项目结构: 工具层:api_keyword/ 参数层:params/ 用例层:case/ 数据驱动:data_driver/ 数据层:data/ 逻…...

【中间件】消息队列中间件intro
中间件middleware 内容管理 introwhy use MQMQ实现漫谈主流消息队列QMQ IntroQMQ架构QMQ 存储模型 本文还是从理论层面分析消息队列中间件 cfeng现在处于理论分析阶段,以中间件例子,之前的blog对于中间件是从使用角度分享了相关的用法,现在就…...
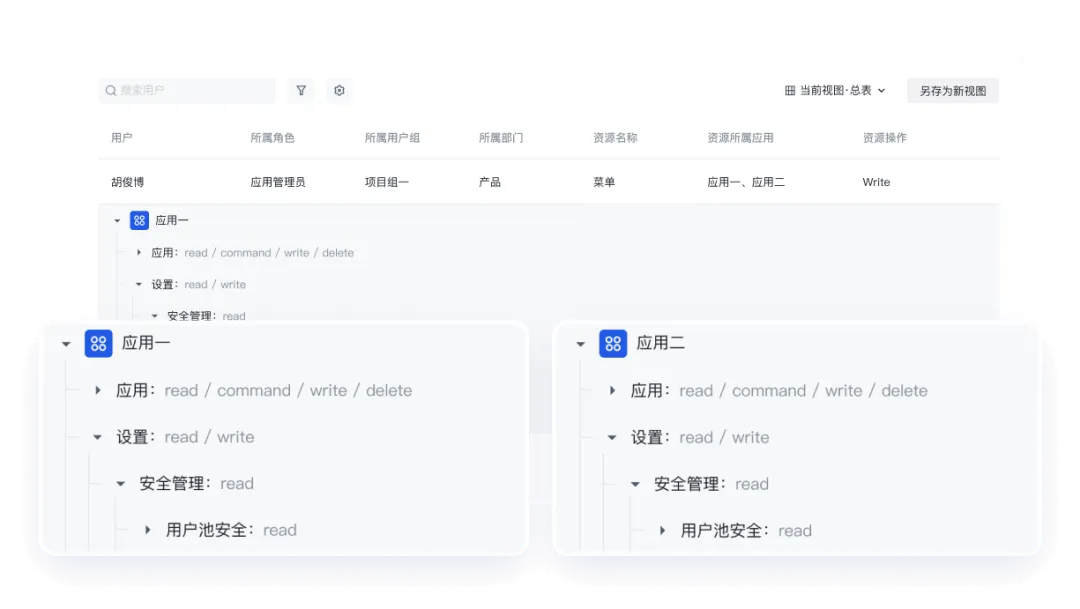
从 RBAC 到 NGAC ,企业如何实现自动化权限管理?
随着各领域加快向数字化、移动化、互联网化的发展,企业信息环境变得庞大复杂,身份和权限管理面临巨大的挑战。为了满足身份管理法规要求并管理风险,企业必须清点、分析和管理用户的访问权限。如今,越来越多的员工采用移动设备进行…...

vue3中如何使用TypeScript?
在Vue 3中引入和使用TypeScript非常简单。下面是在Vue 3中引入和使用TypeScript的步骤: 创建Vue 3项目:首先,使用Vue CLI创建一个新的Vue 3项目。可以使用以下命令: vue create my-project在创建项目时,选择TypeScri…...

Git基础操作:合并某个分支的一个目录到另一个分支
有的时候不小心在错误的分支A上开发了一点代码,也已经提交了;或者分支A原计划先上线的,但是业务调整需要插一个需求进来,但是插进来的需求中有一部分代码在分支A中已经写过了。 这个时候如果想把这部分代码移到正确的分支B上可以…...

学习grdecl文件格式
一、初步了解 最近在学习grdecl文件格式,文档不多。查找资料发现,这个格式的文件是由斯伦贝谢公司的ECLIPSE专业软件生成的。 搜到一些文档,都是2010年之前的,似乎有些用处。文档也交代了这个文件格式分为二进制和文本格式…...
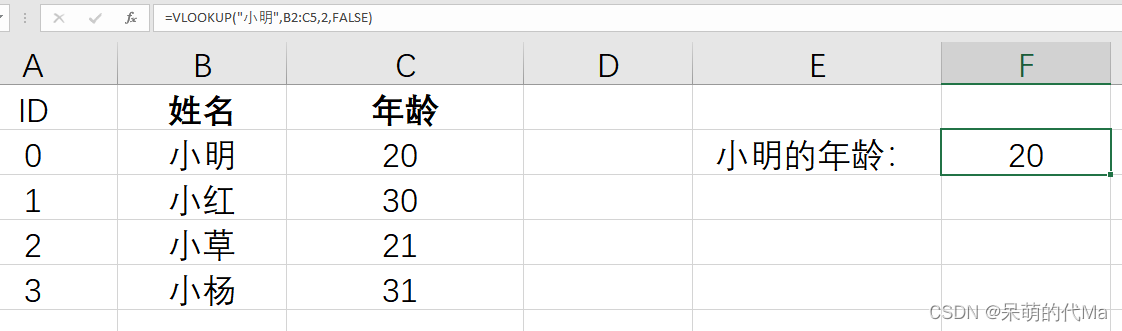
Excel使用VLOOKUP查询数据
VLOOKUP函数在百度百科中的解释是: 解释一下,函数需要4个参数: 参数1(lookup_value):需要匹配的值参数2(table_array):在哪个区域里进行匹配参数3(col_index…...

SpectralGPT: Spectral Foundation Model 论文翻译2
遥感领域的通用大模型 2023.11.13在CVPR发表 原文地址:[2311.07113] SpectralGPT: Spectral Foundation Model (arxiv.org) 实验 在本节中,我们将严格评估我们的SpectralGPT模型的性能,并对其进行基准测试SOTA基础模型:ResN…...

Java编译过程中的JVM
流程 源代码编写: 首先,开发者使用Java编程语言编写源代码。这些源代码通常保存在扩展名为.java的文件中。 编译源代码: 使用Java编译器(例如javac),这些.java文件被编译成Java字节码。字节码是一种中间形…...
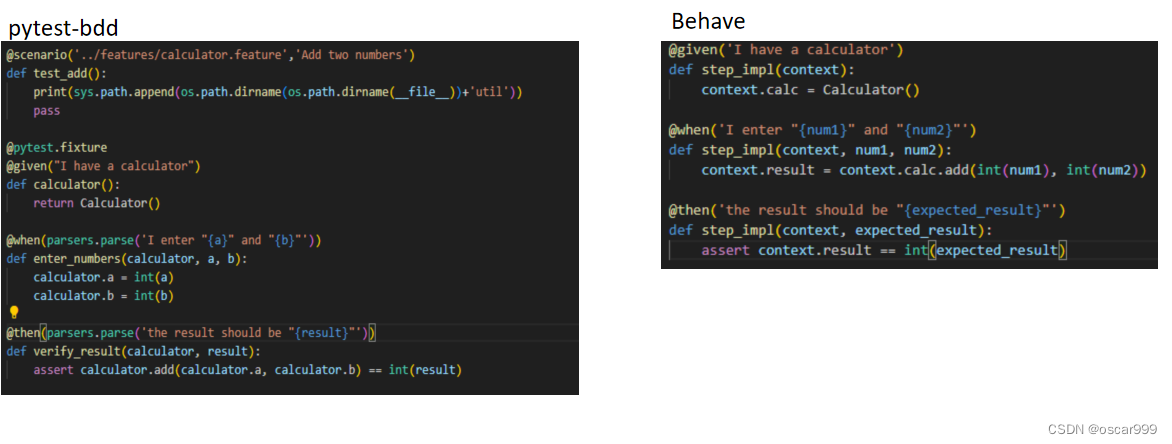
Python BDD 框架比较之 pytest-bdd vs behave
pytest-bdd和behave是 Python 的两个流行的 BDD 测试框架,两者都可以用来编写用户故事和可执行的测试用例, 具体选择哪一个则需要根据实际的项目状况来看。 先简单看一下两者的功能: pytest-bdd 基于pytest测试框架,可以与pytest…...
)
【面经八股】搜广推方向:常见面试题(一)
【面经&八股】搜广推方向:常见面试题(一) 文章目录 【面经&八股】搜广推方向:常见面试题(一)1. 线下效果提升、线上效果不好。2. XGBoost 和 GBDT是什么?有什么区别?3. 偏差与方差。延伸知识(集成学习的三种方式: Bagging、Boosting、Stacking)。4. 随机森林…...
斐讯K2结合Padavan实现锐捷认证破解方法
前言 众所周知,校园网在传统模式下是不能直接插路由使用的,但苦于校园网只能连接一台设备的烦恼,不得不“另辟蹊径”来寻求新的解决路径,这不,它来了,它来了,它带着希望走来了。 本文基于斐讯…...
SpringBoot : ch06 整合 web (一)
前言 SpringBoot作为一款优秀的框架,不仅提供了快速开发的能力,同时也提供了丰富的文档和示例,让开发者更加容易上手。在本博客中,我们将介绍如何使用SpringBoot来整合Web应用程序的相关技术,并通过实例代码来演示如何…...

C++:OJ练习(每日练习系列)
编程题: 题一:把字符串转换成整数 把字符串转换成整数_牛客题霸_牛客网 示例1 输入: "2147483647" 返回值: 2147483647思路一: 第一步:it从str的第一个字符开始遍历,定义一个最后输…...
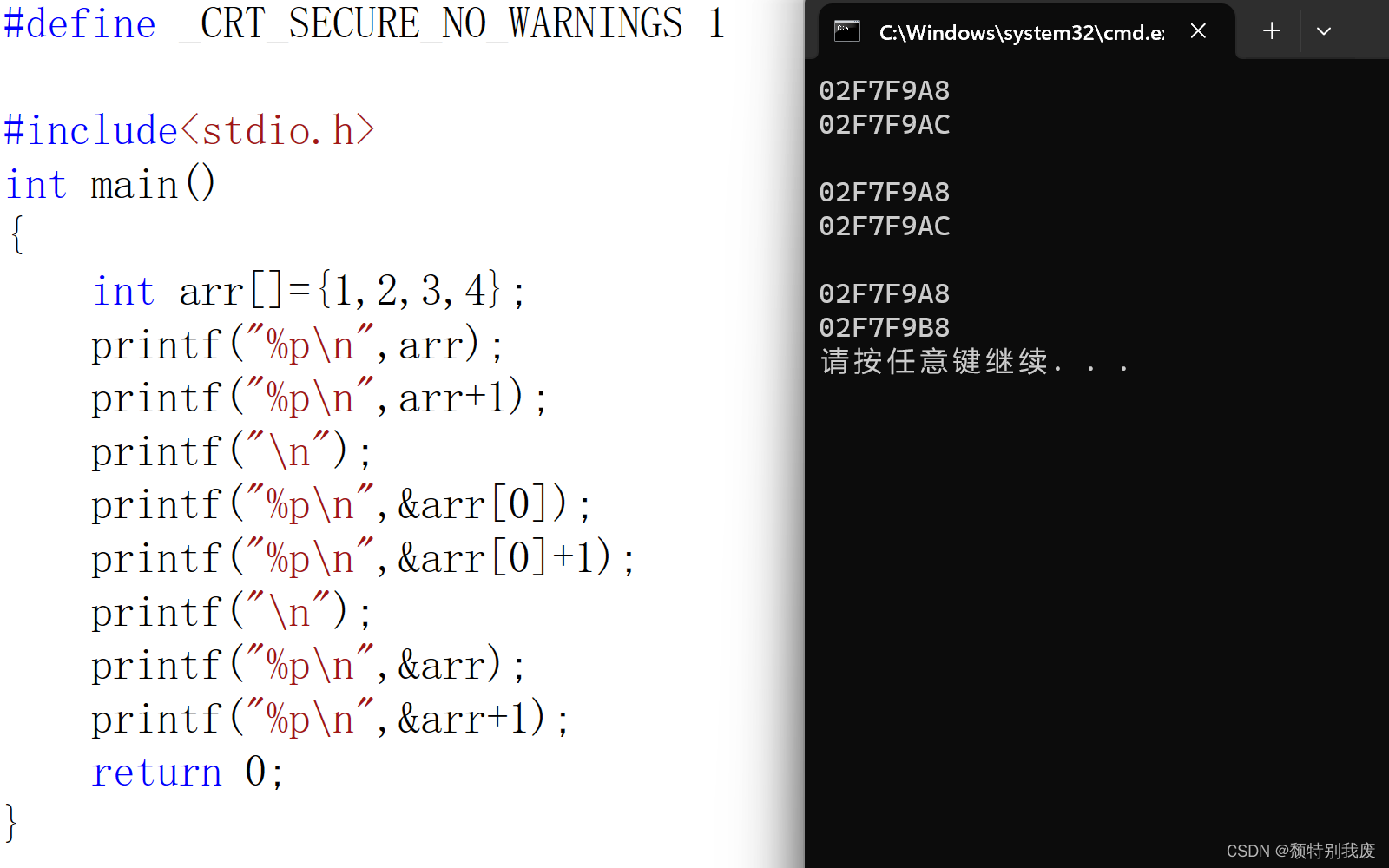
C语言—什么是数组名
#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h> int main() {int arr[]{1,2,3,4};printf("%p\n",arr);printf("%p\n",&arr);printf("%p\n",*arr);return 0; } 结论:数组名是数组首元素地址(下标为0的元素…...

如何与死锁斗争!!!
其他系列文章导航 Java基础合集 设计模式合集 多线程合集 分布式合集 ES合集 文章目录 其他系列文章导航 文章目录 前言 一、死锁场景现场 二、死锁是如何产生的 三、死锁排查思路 四、sql模拟死锁复现 五、死锁的解决方案 前言 为避免影响业务,应尽可能避…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...
