红黑树(万字图文详解)
红黑树
- 1. 红黑树的概念
- 2. 红黑树的性质
- 3. 红黑树节点的定义
- 4. 红黑树结构
- 5. 红黑树的插入操作
- 5.1 按照二叉搜索的树规则插入新节点
- 5.2 检测新节点插入后,红黑树的性质是否造到破坏
- 5.2.1 情况一: cur为红,p为红,g为黑,u存在且为红
- 5.2.2 情况二: cur为红(此时只需要单旋),p为红,g为黑,u不存在/u存在且为黑
- 5.2.3 情况三: cur为红(此时需要进行双旋变成情况二),p为红,g为黑,u不存在/u存在且为黑
- 完整代码
- 6. 红黑树的验证
- 1. 检测其是否满足二叉搜索树(中序遍历是否为有序序列)
- 2. 检测其是否满足红黑树的性质
- 7. 红黑树与AVL树的比较
- 8. 红黑树的应用
注:本文的是在理解AVL树的基础上进行讲解的!
AVL树的实现(万字图文详解)
1. 红黑树的概念
红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。
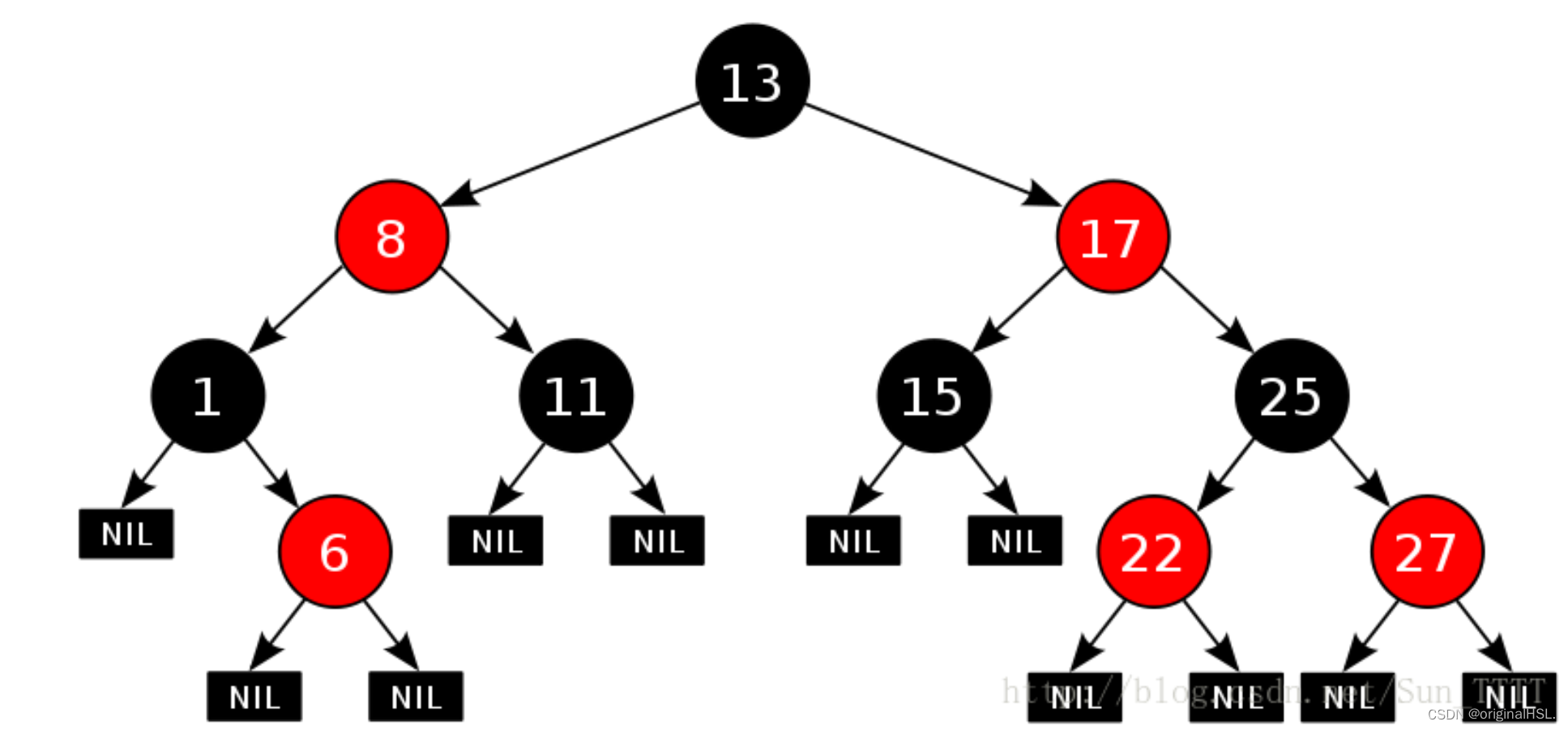
2. 红黑树的性质
1. 每个结点不是红色就是黑色
2. 根节点是黑色的
3. 如果一个节点是红色的,则它的两个孩子结点是黑色的
4. 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均 包含相同数目的黑色结点
5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点)

思考:为什么满足上面的性质,红黑树就能保证:其最长路径中节点个数不会超过最短路径节点个数的两倍?
- 红黑树中的性质确保了任意路径上的黑色节点数量相等,这是红黑树能够保持平衡的关键。根据这个性质,我们可以证明红黑树的最长路径中的节点个数不会超过最短路径的节点个数的两倍。
- 假设红黑树的最短路径上的黑色节点数量为k。由于性质5,任意路径上的黑色节点数量相等,所以最长路径上的黑色节点数量不能少于k个。
- 现在我们来看最长路径上的节点个数。由于性质4,红色节点的两个子节点都是黑色的,因此最长路径上不能有连续的红色节点。而对于红黑树而言,最长路径上的红色节点数量最多为k,因为最长路径上的黑色节点数量不能少于k个。所以最长路径上的节点个数最多为2k,其中k个是黑色节点,k个是红色节点。
- 综上所述,红黑树的最长路径中的节点个数不会超过最短路径的节点个数的两倍,即最长路径上的节点个数最多为2k,其中k为最短路径上的黑色节点数量。
- 这个性质保证了红黑树的高度始终保持在较小的范围内,从而保持了树的平衡性。因为红黑树的高度与最长路径上的节点个数成正比,所以最长路径的节点个数的上限为最短路径的节点个数的两倍,确保了红黑树的平衡性和高效性。
3. 红黑树节点的定义
template<class K, class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Colour _col;int _bf;RBTreeNode(const pair<K, V>& kv):_left(nullptr)//左孩子, _right(nullptr)//右孩子, _parent(nullptr)//父亲, _kv(kv)//存储键值对的成员变量, _col(RED)//默认红色{}
};具体解释如下:
- _left:指向左子节点的指针。
- _right:指向右子节点的指针。
- _parent:指向父节点的指针。
- _kv:存储键值对的成员变量。这里使用了 pair<K, V> 类型来表示键值对,其中 K 是键的类型,V 是值的类型。
- _col:表示节点的颜色。这里使用了 Colour 枚举类型来表示,可能的取值为 RED 或 BLACK,其中 RED 表示红色,BLACK 表示黑色。
- _bf:平衡因子,用于平衡二叉树的调整。
4. 红黑树结构
为了后续实现关联式容器简单,红黑树的实现中增加一个头结点,因为根节点必须为黑色,为了与根节点进行区分,将头结点给成黑色,并且让头结点的 pParent 域指向红黑树的根节点,pLeft域指向红黑树中最小的节点,_pRight域指向红黑树中最大的节点。
如下:
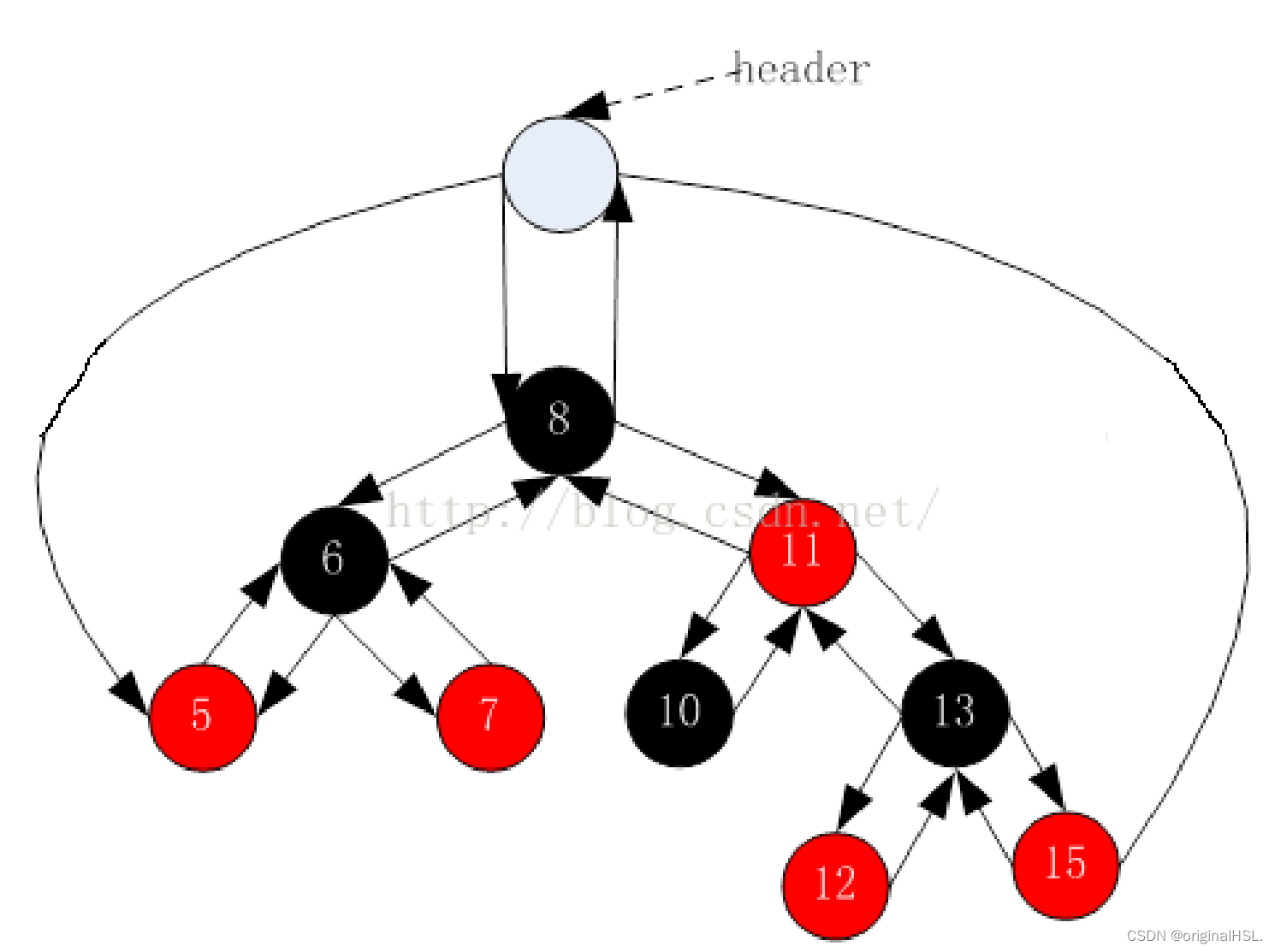
5. 红黑树的插入操作
红黑树是在二叉搜索树的基础上加上其平衡限制条件,因此红黑树的插入可分为两步:
5.1 按照二叉搜索的树规则插入新节点
#pragma once
#include <iostream>
using namespace std;//枚举类型变量
enum Colour
{RED, //红BLACK //黑
};template<class K, class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Colour _col;int _bf;RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED)//默认红色{}
};template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public:bool insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);cur->_col = RED;//!应该能去掉if (parent->_kv.first < kv.first){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}红黑树开整//1.cur为红,parent为红,grandfather为黑,uncle存在且为红//解决方法:p,u变成黑,g变成红,c=g,继续向上调整//2.cur为红,parent为红,grandfather为黑,uncle不存在 or 存在且为黑//解决方法: 单旋:p变红,g变黑,//双旋:c变黑,g变红private:Node* _root = nullptr;
};
5.2 检测新节点插入后,红黑树的性质是否造到破坏
因为新节点的默认颜色是红色,因此:如果其双亲节点的颜色是黑色,没有违反红黑树任何性质,则不需要调整;但当新插入节点的双亲节点颜色为红色时,就违反了性质三不能有连在一起的红色节点,此时需要对红黑树分情况来讨论:

约定:cur为当前节点,p为父节点,g为祖父节点,u为叔叔节点
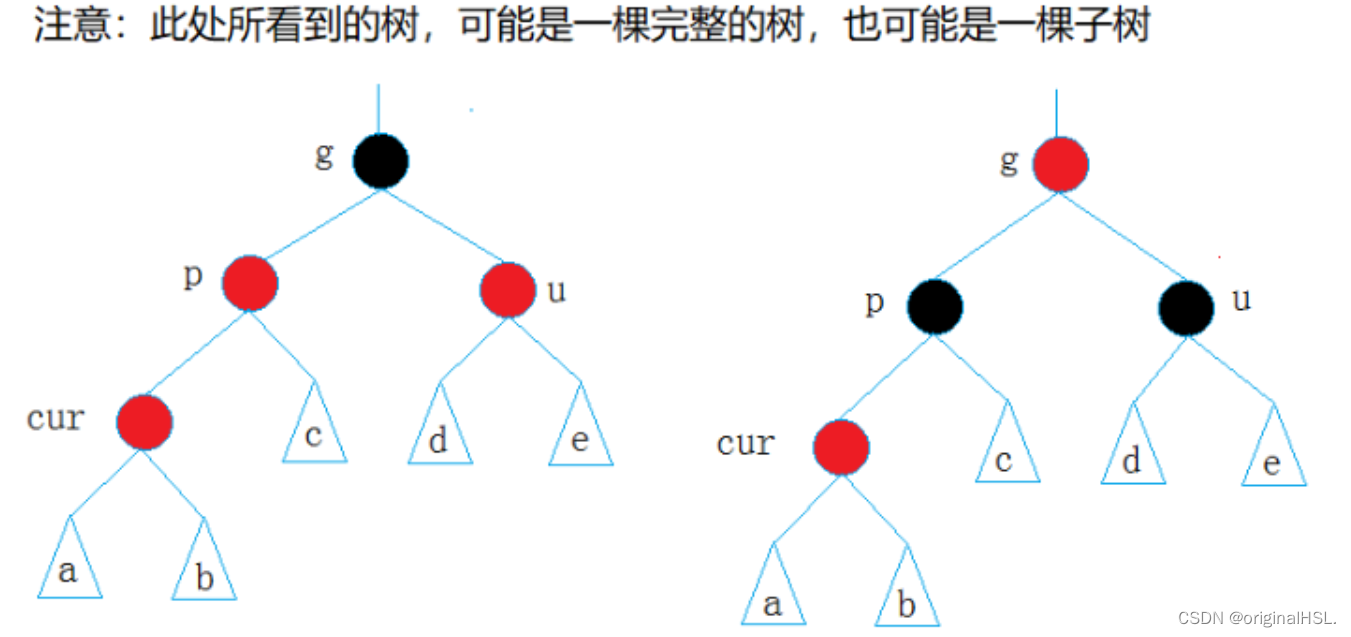
5.2.1 情况一: cur为红,p为红,g为黑,u存在且为红
解决方法:将p,u改为黑,g改为红,然后把g当成cur,继续向上调整。
5.2.2 情况二: cur为红(此时只需要单旋),p为红,g为黑,u不存在/u存在且为黑
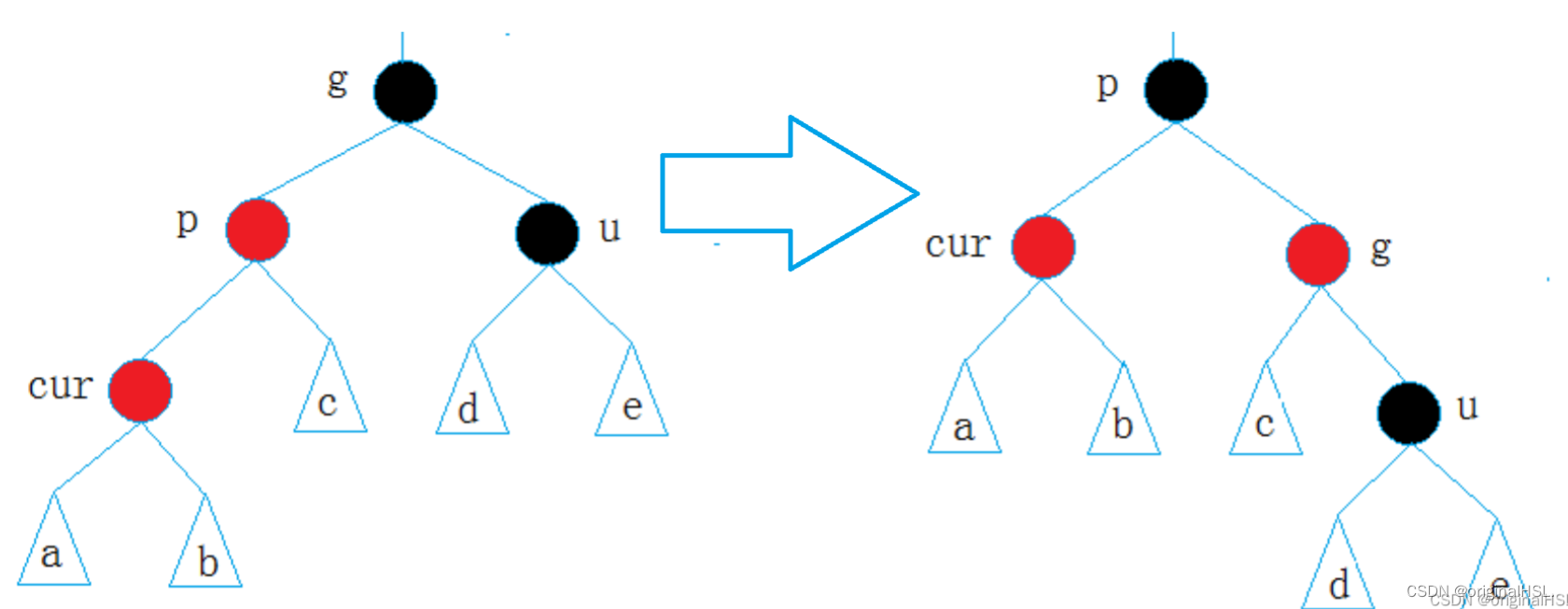

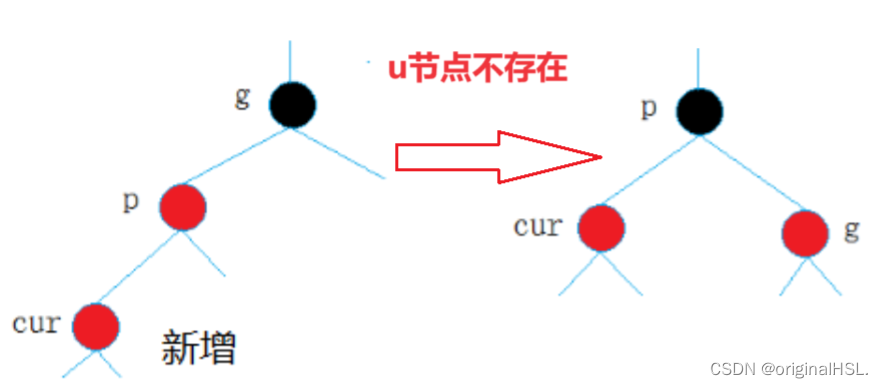
解决方法:
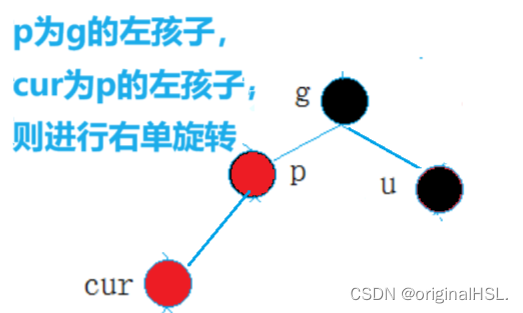
p为g的左孩子,cur为p的左孩子,则进行右单旋转;相反,
p为g的右孩子,cur为p的右孩子,则进行左单旋转
p、g变色–p变黑,g变红

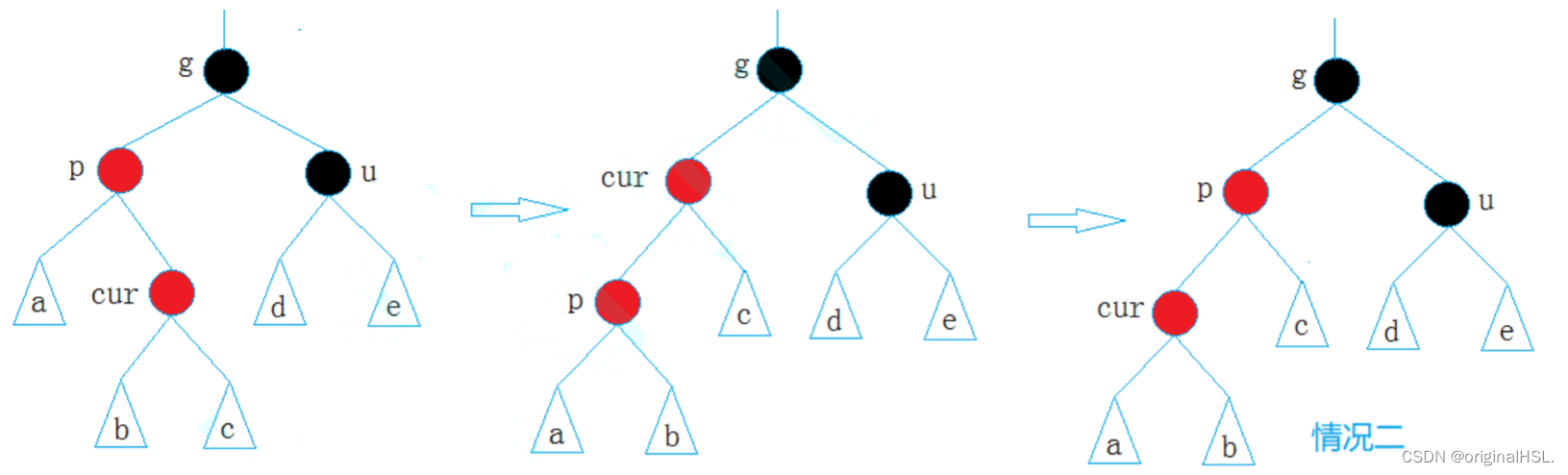
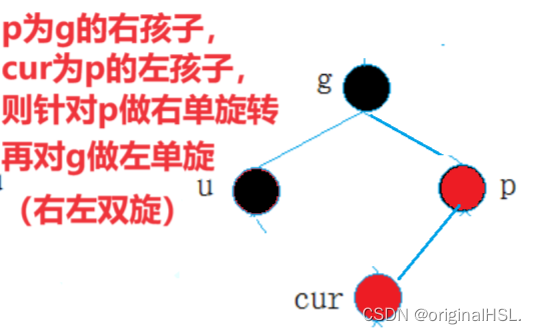
5.2.3 情况三: cur为红(此时需要进行双旋变成情况二),p为红,g为黑,u不存在/u存在且为黑
解决方法:
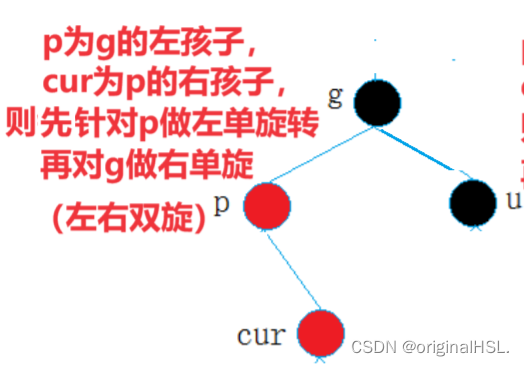
- p为g的左孩子,cur为p的右孩子,则针对p做左单旋转,再对g右单旋即可完成调整;
- 相反,
p为g的右孩子,cur为p的左孩子,则针对p做右单旋转
,再对g左单旋即可完成调整
完整代码
#pragma once
#include <iostream>
using namespace std;//枚举类型变量
enum Colour
{RED, //红BLACK //黑
};template<class K, class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Colour _col;int _bf;RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED)//默认红色{}
};template<class K, class V>
class RBTree
{typedef RBTreeNode<K, V> Node;
public:bool insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);cur->_col = RED;//!应该能去掉if (parent->_kv.first < kv.first){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}红黑树开整//1.cur为红,parent为红,grandfather为黑,uncle存在且为红//解决方法:p,u变成黑,g变成红,c=g,继续向上调整//2.cur为红,parent为红,grandfather为黑,uncle不存在 or 存在且为黑//解决方法: 单旋:p变红,g变黑,//双旋:c变黑,g变红//parent不为空,且parent->_col==RED(这样保证肯定有祖先,也就是grandfather不为空)while (parent && parent->_col == RED){// g// p u//cNode* grandfather = parent->_parent;if (parent == grandfather->_left){// g// p u//cNode* uncle = grandfather->_right;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//继续往上更新处理cur = grandfather;parent = cur->_parent;//这儿parent更新完之后可能为空,为空就结束}else//uncle不存在 or 存在且为黑{ //单旋// g// p u//cif (cur == parent->_left){RotateR(grandfather);parent->_col = BLACK;//p变黑grandfather->_col = RED;//g变红}else if (cur == parent->_right){//双旋// g// p u// cRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}// g// u p// celse// parent == grandfather->_left{Node* uncle = grandfather->_left;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//继续往上更新处理cur = grandfather;parent = cur->_parent;}else//(uncle不存在 or 存在且为黑){ //单旋// g // u p // c if (cur == parent->_right){RotateL(grandfather);parent->_col = BLACK;//p变黑grandfather->_col = RED;//g变红} else//cur == parent->_left {//双旋// g// u p// c RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}//管你根节点更新成啥了,管你个求,直接把_root->_col改成黑色_root->_col = BLACK;return true;}//左单旋//(1.父亲节点的右边等于右孩子的左边; 2.右孩子的左边等于父亲节点)//【把右孩子的左边给给父亲节点的右边; 2.再把父亲节点给给右孩子的左边】void RotateL(Node* parent){Node* SubR = parent->_right;Node* SubRL = SubR->_left;//旋转链接parent->_right = SubRL;SubR->_left = parent;Node* Parent_Parent = parent->_parent;parent->_parent = SubR;if (SubRL){SubRL->_parent = parent;}//和父节点的父节点链接if (_root == parent){_root = SubR;SubR->_parent = nullptr;}else{if (Parent_Parent->_left == parent){Parent_Parent->_left = SubR;}else{Parent_Parent->_right = SubR;}SubR->_parent = Parent_Parent;}}//右单旋void RotateR(Node* parent){Node* SubL = parent->_left;Node* SubLR = SubL->_right;//旋转链接//动一个节点就把他的父亲也变动parent->_left = SubLR;if (SubLR)//SubLR可能为空{SubLR->_parent = parent;}Node* Parent_Parent = parent->_parent;SubL->_right = parent;parent->_parent = SubL;//和父节点的父节点链接if (_root == parent){_root = SubL;SubL->_parent = nullptr;}else{if (Parent_Parent->_left == parent){Parent_Parent->_left = SubL;}else{Parent_Parent->_right = SubL;}SubL->_parent = Parent_Parent;//链接}}void InOrder(){_InOrder(_root);cout << endl;}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_kv.first << " ";_InOrder(root->_right);}//根节点到当前这条路径的黑色节点个数bool Check(Node *root,int blacknum,const int RefVal){if (root == nullptr){if (blacknum != RefVal){return false;}return true;}//直接反向检查,儿子很复杂,父亲只有一个if (root->_col == RED && root->_parent->_col == RED){cout<<"有连续的红节点" << endl;return false;}if (root->_col == BLACK){blacknum++;}return Check(root->_left, blacknum, RefVal) && Check(root->_right, blacknum, RefVal);}bool IsBalance(){if (_root == nullptr){return true;}if (_root->_col == RED){return false;}int blacknum = 0;//记录每条路径的黑色节点个数int RefVal = 0;//定一个标准Node* cur = _root;while (cur)//改了一个bug ,之前这儿脑子抽抽了,写成了if{if (cur->_col == BLACK){++RefVal;}cur = cur->_left;}return Check(_root, blacknum,RefVal);}private:Node* _root = nullptr;
};
6. 红黑树的验证
红黑树的检测分为两步:
1. 检测其是否满足二叉搜索树(中序遍历是否为有序序列)
#include <vector>
#include "RBTree.h"int main()
{int arr[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };RBTree<int, int> a;for (auto e : arr){a.insert(make_pair(e, e));}a.InOrder();return 0;
}

2. 检测其是否满足红黑树的性质
我们可以通过递归地遍历红黑树的节点,并统计根节点到每个叶子节点路径上的黑色节点个数来进行检查。
//根节点到当前这条路径的黑色节点个数
bool Check(Node *root,int blacknum,const int RefVal)
{if (root == nullptr){if (blacknum != RefVal){return false;}return true;}//直接反向检查,儿子很复杂,父亲只有一个if (root->_col == RED && root->_parent->_col == RED){cout<<"有连续的红节点" << endl;return false;}if (root->_col == BLACK){blacknum++;}return Check(root->_left, blacknum, RefVal) && Check(root->_right, blacknum, RefVal);
}bool IsBalance()
{if (_root == nullptr){return true;}if (_root->_col == RED){return false;}int blacknum = 0;//记录每条路径的黑色节点个数int RefVal = 0;//定一个标准Node* cur = _root;while (cur)//改了一个bug ,之前这儿脑子抽抽了,写成了if{if (cur->_col == BLACK){++RefVal;}cur = cur->_left;}return Check(_root, blacknum,RefVal);
}
函数讲解
Check 函数是一个递归函数,用于检查从当前节点到叶子节点的路径上的黑色节点个数是否与参考值 RefVal 相等。参数 root 表示当前节点指针,blacknum 表示根节点到当前节点的路径上的黑色节点个数,RefVal 是参考值。
- 如果当前节点为空指针,即到达了叶子节点,那么检查路径上的黑色节点个数 blacknum 是否等于参考值 RefVal,如果不相等则返回 false,否则返回 true。
- 如果当前节点的颜色为红色,并且父节点也是红色,表示存在连续的红节点,不符合红黑树的性质,返回 false。
- 如果当前节点的颜色为黑色,将 blacknum 值加一。
- 递归地调用 Check 函数检查左子节点和右子节点,并将当前节点的黑色节点个数 blacknum 作为参数传递。
IsBalance 函数用于检查整个红黑树是否符合红黑树的性质。
- 如果红黑树为空树,即根节点为空,认为是一棵合法的红黑树,返回 true。
- 如果根节点的颜色是红色,违反了红黑树的性质,返回 false。
- 初始化 blacknum 为 0,用于记录每条路径的黑色节点个数。
- 初始化 RefVal 为 0,作为参考值。
- 通过遍历从根节点到最左子节点的路径,统计参考值 RefVal,即路径上的黑色节点个数。
- 调用 Check 函数,传入根节点、路径上的黑色节点个数 blacknum 和参考值 RefVal 进行检查。
#include <vector>
#include "RBTree.h"
int main()
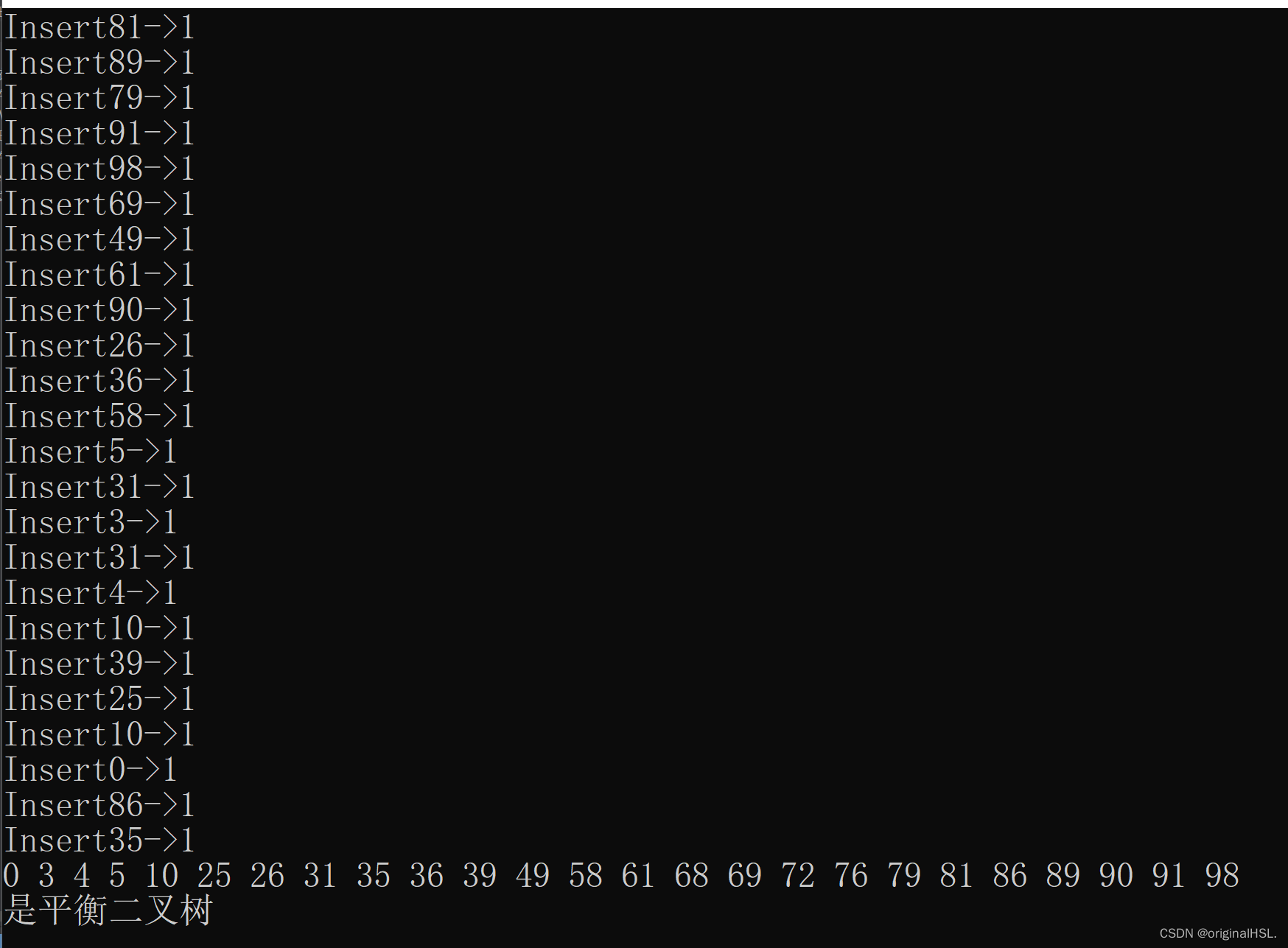
{const int N = 30;vector<int> v;v.reserve(N);srand(time(0));for (size_t i = 0; i < N; i++){v.push_back(rand()%100 );}RBTree<int, int> t;for (auto e : v){if (e == 0){int i = 0;}t.insert(make_pair(e, e));cout << "Insert" << e << "->" << t.IsBalance() << endl;}t.InOrder();//中序打印if (t.IsBalance()){cout << "是平衡二叉树" << endl;}else{cout << "不是平衡二叉树" << endl;}return 0;
}
7. 红黑树与AVL树的比较
红黑树和AVL树都是高效的平衡二叉树,增删改查的时间复杂度都是O( l o g 2 N log_2 N log2N),红黑树不追求绝对平衡,其只需保证最长路径不超过最短路径的2倍,相对而言,降低了插入和旋转的次数,所以在经常进行增删的结构中性能比AVL树更优,而且红黑树实现比较简单,所以实际运用中红黑树更多。
8. 红黑树的应用
-
C++ STL库 – map/set、mutil_map/mutil_set
C++ STL中的std::map和std::set:这些容器类通常使用红黑树作为底层数据结构,提供了高效的查找、插入和删除操作。 -
数据库系统:红黑树常被用作数据库索引结构,例如在关系型数据库中,可以使用红黑树来实现B+树索引,提供高效的数据检索和排序功能。
-
线程调度器:操作系统中的线程调度器通常需要高效地管理和调度线程,红黑树可用于实现定时器和任务调度器,以快速查找和处理就绪的线程。
-
路由算法:在网络路由算法中,红黑树可以用于快速查找最佳路径和路由表项,提供高效的路由查找和转发功能。
-
linux内核
文件系统:某些文件系统使用红黑树来管理文件和目录的索引,以支持快速的文件查找和访问。 -
编译器和解释器:在编译器和解释器中,红黑树可以用于符号表的实现,以支持快速的符号查找和关联。
-
并发数据结构:在多线程和并发编程中,红黑树可以用于实现并发安全的数据结构,例如并发哈希表、并发有序集合等。
(本章完)
相关文章:

红黑树(万字图文详解)
红黑树 1. 红黑树的概念2. 红黑树的性质3. 红黑树节点的定义4. 红黑树结构5. 红黑树的插入操作5.1 按照二叉搜索的树规则插入新节点5.2 检测新节点插入后,红黑树的性质是否造到破坏5.2.1 情况一: cur为红,p为红,g为黑,u存在且为红…...
Kotlin学习——kt入门合集博客 kt里的委派模式Delegation kt里的特性
Kotlin 是一门现代但已成熟的编程语言,旨在让开发人员更幸福快乐。 它简洁、安全、可与 Java 及其他语言互操作,并提供了多种方式在多个平台间复用代码,以实现高效编程。 https://play.kotlinlang.org/byExample/01_introduction/02_Functio…...

数据挖掘 朴素贝叶斯
直入正题,直接看代码: 这是一段判断是不是藏话的代码 import numpy as np# 数据采集(定义函数加载数据集) def load_dataset():sent_list [[my, name, is, Devin],[you, are, stupid],[my, boyfriend, is, SB],[you, looks, ver…...

UI自动化测试工具有哪些优势?
UI自动化测试工具通过提高测试效率、覆盖率,减少测试时间和成本,以及支持持续集成等方式,为软件开发团队提供了一系列重要的优势,有助于提升软件质量和开发效率。 自动化执行:UI自动化测试工具可以模拟用户与应用程序的…...

【论文阅读笔记】InstructDiffusion: A Generalist Modeling Interface for Vision Tasks
【论文阅读笔记】StyleAvatar3D: Leveraging Image-Text Diffusion Models for High-Fidelity 3D Avatar Generation 论文阅读笔记论文信息引言动机挑战 方法结果 关键发现相关工作1. 视觉语言基础模型2. 视觉通用模型 方法/模型视觉任务的统一说明训练数据构建网络结构 实验设…...

笔记62:注意力汇聚 --- Nadaraya_Watson 核回归
本地笔记地址:D:\work_file\(4)DeepLearning_Learning\03_个人笔记\3.循环神经网络\第10章:动手学深度学习~注意力机制 a a a a a a a a a a a a a a a a...

给定一个n×n的方阵,本题要求计算该矩阵除副对角线、最后一列和最后一行以外的所有元素之和。
7-5 矩阵运算 分数 20 全屏浏览题目 切换布局 作者 C课程组 单位 浙江大学 给定一个nn的方阵,本题要求计算该矩阵除副对角线、最后一列和最后一行以外的所有元素之和。副对角线为从矩阵的右上角至左下角的连线。 输入格式: 输入第一行给出正整数n(…...

Go语言的学习笔记3——Go语言项目布局
Go 1.11 版本开始引入 go.mod 和 go.sum 以支持Go Module构建机制,而这种机制成为官方的依赖包管理方式。 现在Go可执行程序项目的典型布局如下所示: exe-layout ├── cmd/ │ ├── app1/ │ │ └── main.go │ └── app2/ │ └…...

70-76-堆、贪心算法
LeetCode 热题 100 文章目录 LeetCode 热题 100堆70. 中等-数组中的第K个最大元素71. 中等-前K个高频元素72. 困难-数据流中的中位数 贪心算法73. 简单-买卖股票的最佳时机74. 中等-跳跃游戏75. 中等-跳跃游戏II76. 中等-划分字母区间 本文存储我刷题的笔记。 堆 70. 中等-数组…...

Qt Network
Qt Network Qt Network为使用TCP/IP的应用程序编程提供了一组API。各种C++类处理诸如请求、cookies和通过HTTP发送数据之类的操作。 标题使用模块 使用Qt模块需要直接或通过其他依赖项链接到模块库。一些构建工具对此有专门的支持,包括CMake和qmake. 标题使用CMake构建 使…...
Win10电脑用U盘重装系统的步骤
在Win10电脑中,用户遇到了无法解决的系统问题,用户这时候就可以考虑重装Win10系统,这样即可轻松解决问题,从而满足自己的操作需求。接下来小编给大家详细介绍关于Win10电脑中用U盘重装系统的教程步骤。 准备工作 1. 一台正常联网可…...

安防视频监控/磁盘阵列/集中云存储平台EasyCVR设备录像保活不生效原因是什么?该如何解决?
安防视频监控/视频集中存储/云存储/磁盘阵列EasyCVR平台可拓展性强、视频能力灵活、部署轻快,可支持的主流标准协议有国标GB28181、RTSP/Onvif、RTMP等,以及支持厂家私有协议与SDK接入,包括海康Ehome、海大宇等设备的SDK等。平台既具备传统安…...
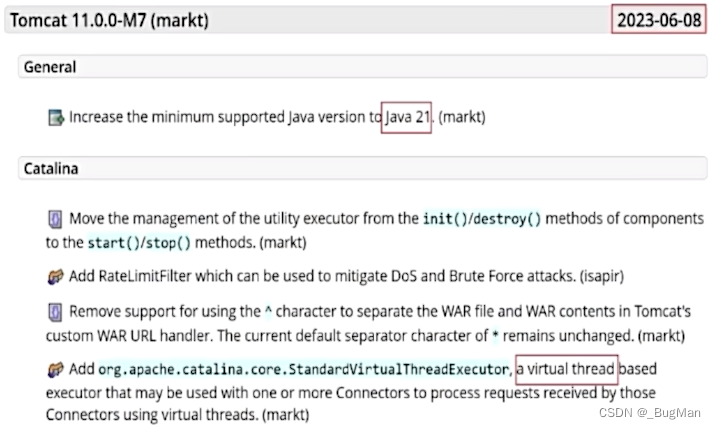
【JDK21】详解虚拟线程
目录 1.概述 2.虚拟线程是为了解决哪些问题 2.1.线程切换的巨大代价 2.2.哪些情况会造成线程的切换 2.3.线程资源是有限的 3.虚拟线程 4.适用场景 1.概述 你发任你发,我用JAVA8?JDK21可能要对这句话say no了。 现在Oracle JDK是每4个版本&#x…...
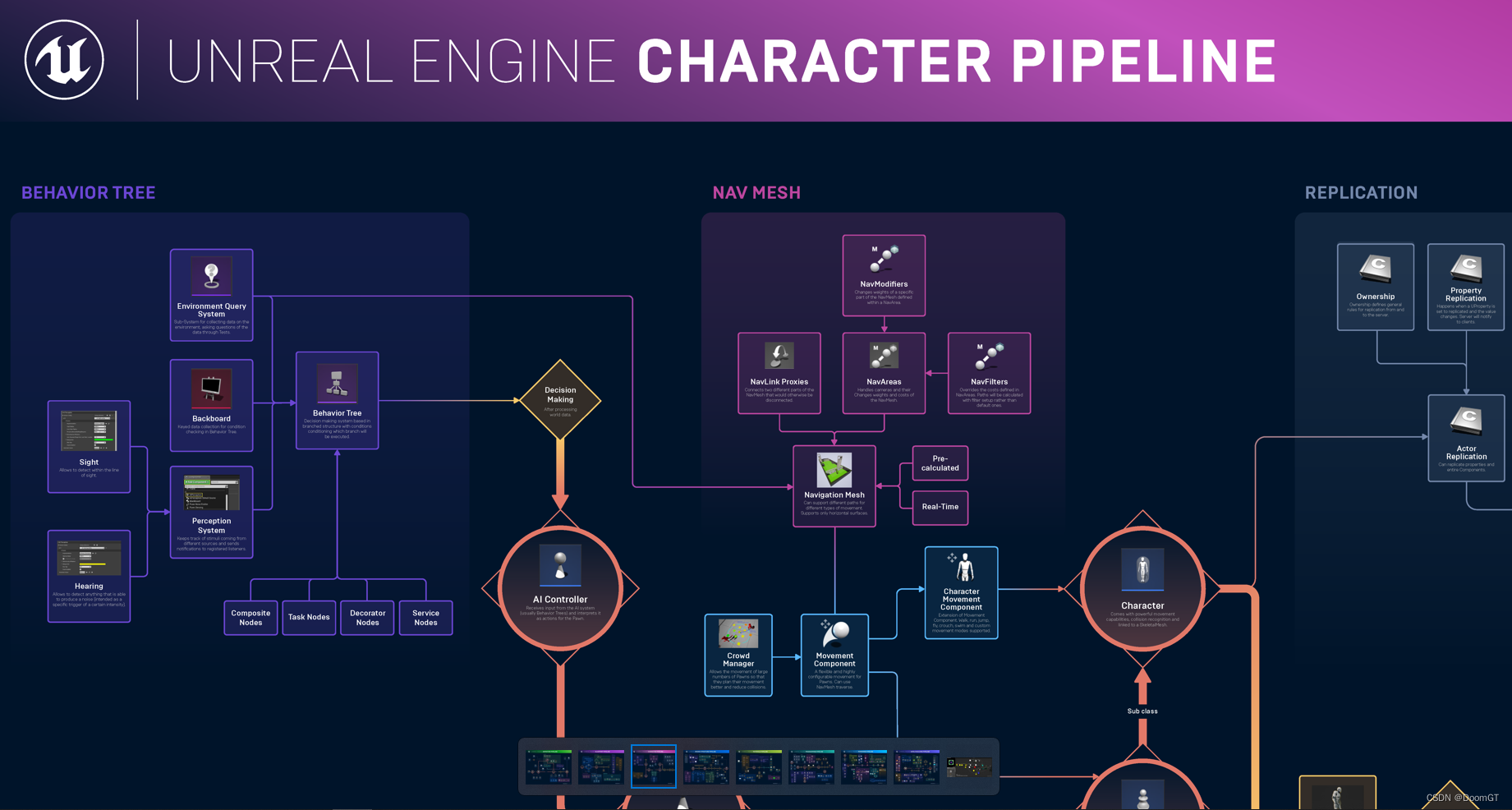
UE5 - 虚幻引擎各模块流程图
来自虚幻官方的一些资料,分享一下; 一些模块的流程图,比如动画模块: 或角色相关流程: 由于图片比较大,上传到了网络,可自取: 链接:https://pan.baidu.com/s/1BQ2KiuP08c…...
vue3实现element table缓存滚动条
背景 对于后台管理系统,数据的展示形式大多都是通过表格,常常会出现的一种场景,从表格跳到二级页面,再返回上一页时,需要缓存当前的页码和滚动条的位置,以为使用keep-alive就能实现这两种诉求,…...
)
flutter布局详解及代码示例(下)
布局 基本布局 GridView(二维滚动列表):比ListView多了一个方向的数据填充。ListBody(滚动列表):相比ListView,没有回收复用,简单易用。Table(表格布局)&am…...

SQL Server:流程控制语言详解
文章目录 一、批处理、脚本和变量局部变量和全局变量1、局部变量2、全局变量 二、顺序、分支和循环结构语句1、程序注释语句2、BEGIN┅END语句块3、IF┅ELSE语句4、CASE语句5、WHILE语句6、BREAK和CONTINUE语句BREAK语句CONTINUE语句 三、程序返回、屏幕显示等语句1、RETURN语句…...
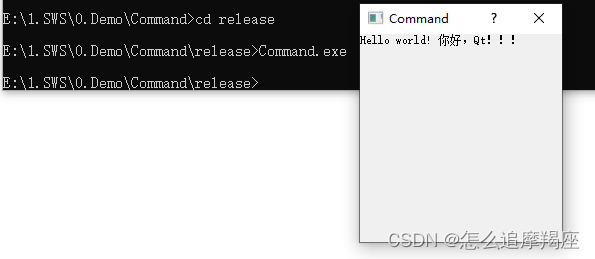
2、用命令行编译Qt程序生成可执行文件exe
一、创建源文件 1、新建一个文件夹,并创建一个txt文件 2、重命名为main.cpp 3、在main.cpp中添加如下代码 #include <QApplication> #include <QDialog> #include <QLabel> int main(int argc, char *argv[]) { QApplication a(argc, argv); QDi…...

【追求卓越08】算法--排序算法
引导 今天开始介绍我们在工作中经常遇到的算法--排序。排序算法有很多,我们主要介绍以下几种: 冒泡排序 插入排序 选择排序 归并排序 快速排序 计数排序 基数排序 桶排序 我们需要了解每一种算法的定义以及实现方式,并且掌握如何评…...
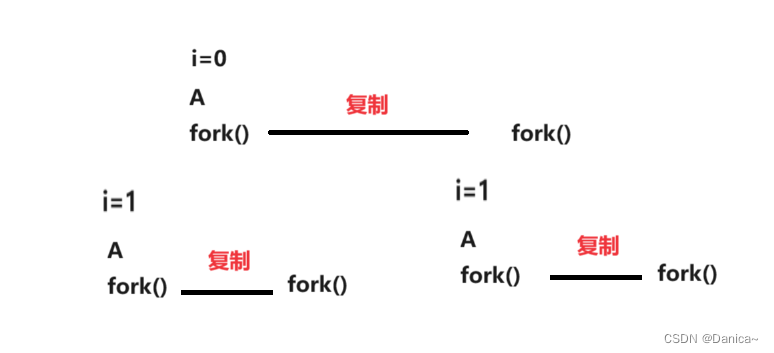
Linux fork笔试练习题
1.打印结果? #include <stdio.h> #include <unistd.h> #include <stdlib.h>int main() {int i0;for(;i<2;i){fork();printf("A\n");}exit(0); } 结果打印 A A A A A A 2.将上面的打印的\n去掉,结果如何? printf("…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

ssc377d修改flash分区大小
1、flash的分区默认分配16M、 / # df -h Filesystem Size Used Available Use% Mounted on /dev/root 1.9M 1.9M 0 100% / /dev/mtdblock4 3.0M...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...
