数据结构:字典树(前缀树,Trie树),压缩字典树(Radix)
字典树Trie Tree
字典树也称前缀树,Trie树。在 Elasticsearch 的倒排索引中用的也是 Trie 树。是一种针对字符串进行维护的数据结构。
字典树是对词典的一种存储方式,这个词典中的每个“单词”就是从根节点出发一直到某一个目标节点的路径,路径中每个字母连起来就是一个单词。因此它能利用字符串的公共前缀来节省存储空间。
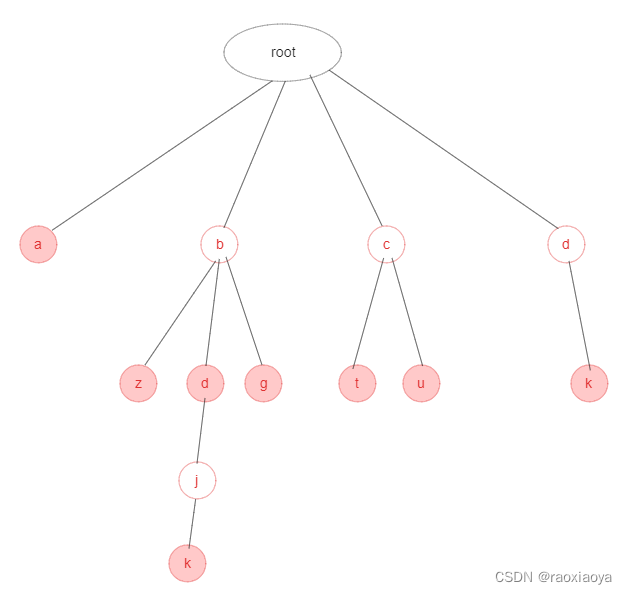
红色代表有单词在这里结束,因此需要有个标记。上图可以匹配的字符串有:
a
bz
bd
bdjk
bg
ct
cu
dk
具体实现
package mainimport "fmt"type Node struct {nodeId int // 节点的全局IDexist bool // 是否有单词在这里结束
}// 255 表示每个节点最多有255个子节点,因为 ASCII 码目前是两个字节,
// 这样做会有一定的空间浪费,但是便于理解,也可以进一步优化。
type Nodes [255]Node// 每个子节点都是数组结构,最终存储到一个map中。
// 层层查找:nodeId -> indexId -> nodeId -> indexId ->...
type Tree struct {nodes map[int]NodescurrentNodeId int // 自增ID
}func (tree *Tree) insert(str string) {var parentNode Nodefor i := 0; i < len(str); i++ {subIndex := str[i]if _, ok := tree.nodes[parentNode.nodeId]; !ok {var subNode Nodestree.nodes[parentNode.nodeId] = subNode}nds := tree.nodes[parentNode.nodeId]var needUpdate boolif nds[subIndex].nodeId == 0 {tree.currentNodeId++nds[subIndex].nodeId = tree.currentNodeIdneedUpdate = true}if i == len(str)-1 {nds[subIndex].exist = trueneedUpdate = true}if needUpdate == true {tree.nodes[parentNode.nodeId] = nds}// fmt.Println(string(subIndex), nds[subIndex]) // 调试输出parentNode = nds[subIndex]}
}func (tree *Tree) Exist(str string) bool {var parentNode Nodefor i := 0; i < len(str); i++ {subIndex := str[i]if _, ok := tree.nodes[parentNode.nodeId]; !ok {return false}nds := tree.nodes[parentNode.nodeId]if nds[subIndex].nodeId == 0 {return false}parentNode = nds[subIndex]}return parentNode.exist
}func main() {tree := &Tree{nodes: make(map[int]Nodes),}tree.insert("abcdefg")tree.insert("ab")tree.insert("123456789")tree.insert("123456")fmt.Println(tree.Exist("ab")) // truefmt.Println(tree.Exist("abc")) // falsefmt.Println(tree.Exist("123456789")) // truefmt.Println(tree.Exist("123456")) // true
}压缩字典树 Radix Tree
Radix树,即基数树,也称压缩字典树,是一种提供key-value存储查找的数据结构。radix tree常用于快速查找的场景中,例如:redis中存储slot对应的key信息、内核中使用radix tree管理数据结构、大多数http的router通过radix管理路由。Radix树在Trie Tree(字典树)的原理上优化过来的。
虽然Trie Tree具有比较高的查询效率,但是从上图可以看到,有许多结点只有一个子结点。这种情况是不必要的,不但影响了查询效率(增加了树的高度),主要是浪费了存储空间。完全可以将这些结点合并为一个结点,这就是Radix树的由来。Radix树将只有一个子节点的中间节点将被压缩,使之具有更加合理的内存使用和查询的效率。
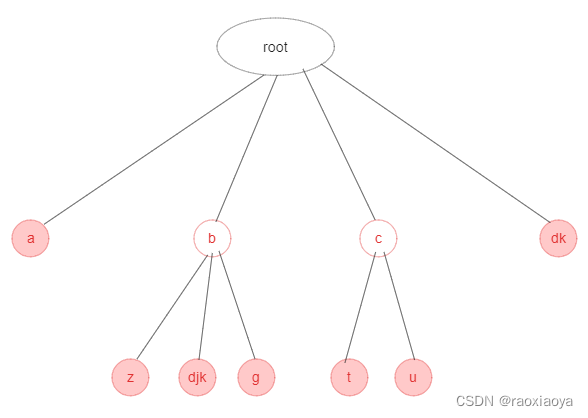
相关文章:

数据结构:字典树(前缀树,Trie树),压缩字典树(Radix)
字典树Trie Tree 字典树也称前缀树,Trie树。在 Elasticsearch 的倒排索引中用的也是 Trie 树。是一种针对字符串进行维护的数据结构。 字典树是对词典的一种存储方式,这个词典中的每个“单词”就是从根节点出发一直到某一个目标节点的路径,…...

前端学习系列之html
目录 初识html 发展史 优势 W3C 标准 地址 格式 网页基本标签 标题标签 段落标签 换行标签 水平线标签 字体样式 注释和特殊符号 特殊符号 图像、超链接 图像 常见图像格式 格式 超链接 格式 重要属性 href:规定链接指向的页面的 URL target…...
Star History 十月开源精选 |AI for Postgres
在 2023 年 Stack Overflow 开发者调查中,Postgres 顶替了 MySQL 被评为最受欢迎的数据库。一个重要因素应该是 Postgres 支持扩展:可扩展的架构 Postgres 仍然由社区拥有,Postgres 生态近年来蓬勃发展。 扩展可以看作是内置功能,…...
网络运维与网络安全 学习笔记2023.11.23
网络运维与网络安全 学习笔记 第二十四天 今日目标 VRRP负载均衡、BFD原理与配置、BFD典型应用 DHCP工作原理、全局模式DHCP VRRP负载均衡 VRRP单组缺陷 每网段存在一个VRRP组,缺点如下: 主网关数据转发压力大 备份网关不转发任何数据 网络设备利用…...
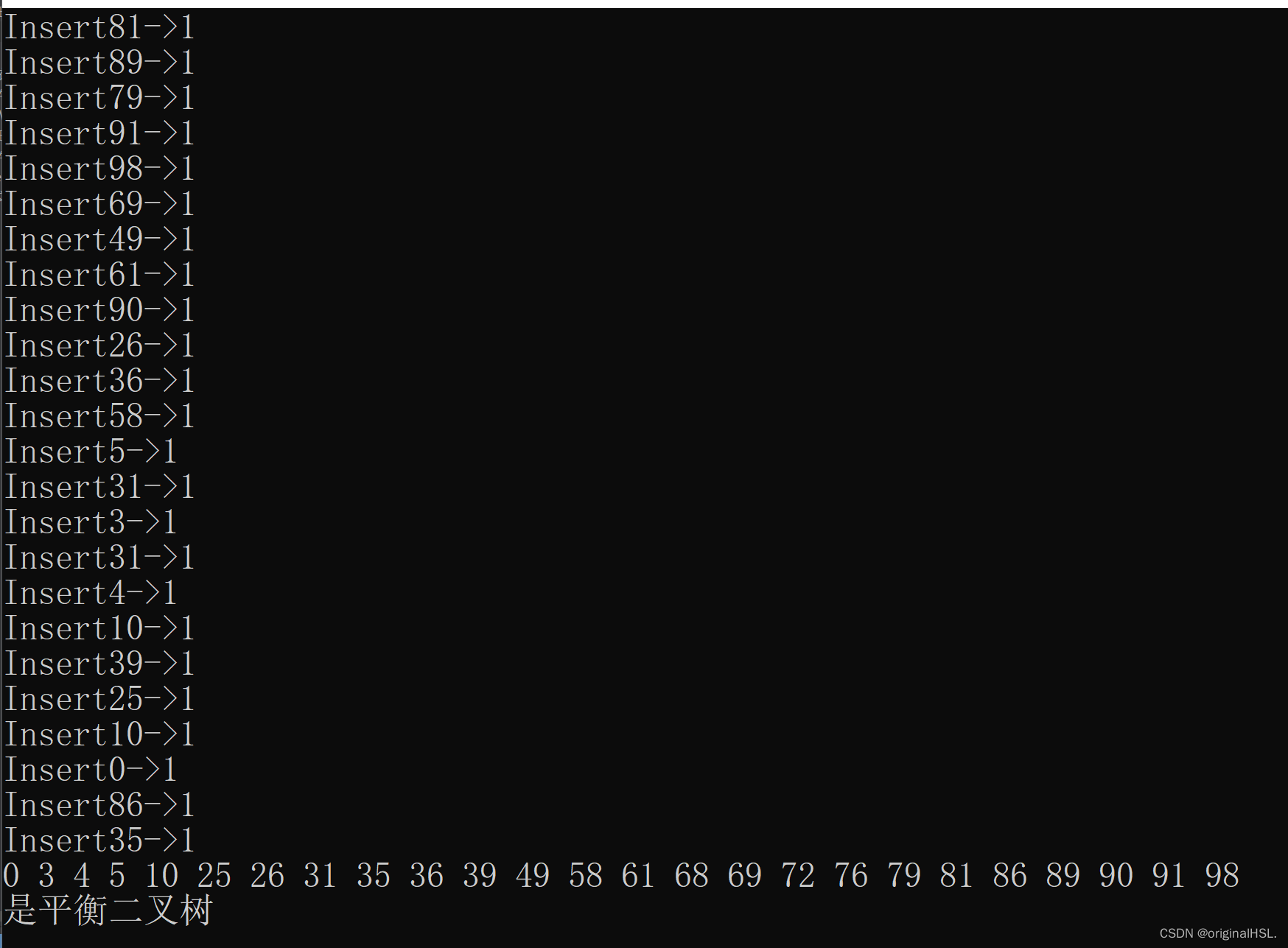
红黑树(万字图文详解)
红黑树 1. 红黑树的概念2. 红黑树的性质3. 红黑树节点的定义4. 红黑树结构5. 红黑树的插入操作5.1 按照二叉搜索的树规则插入新节点5.2 检测新节点插入后,红黑树的性质是否造到破坏5.2.1 情况一: cur为红,p为红,g为黑,u存在且为红…...
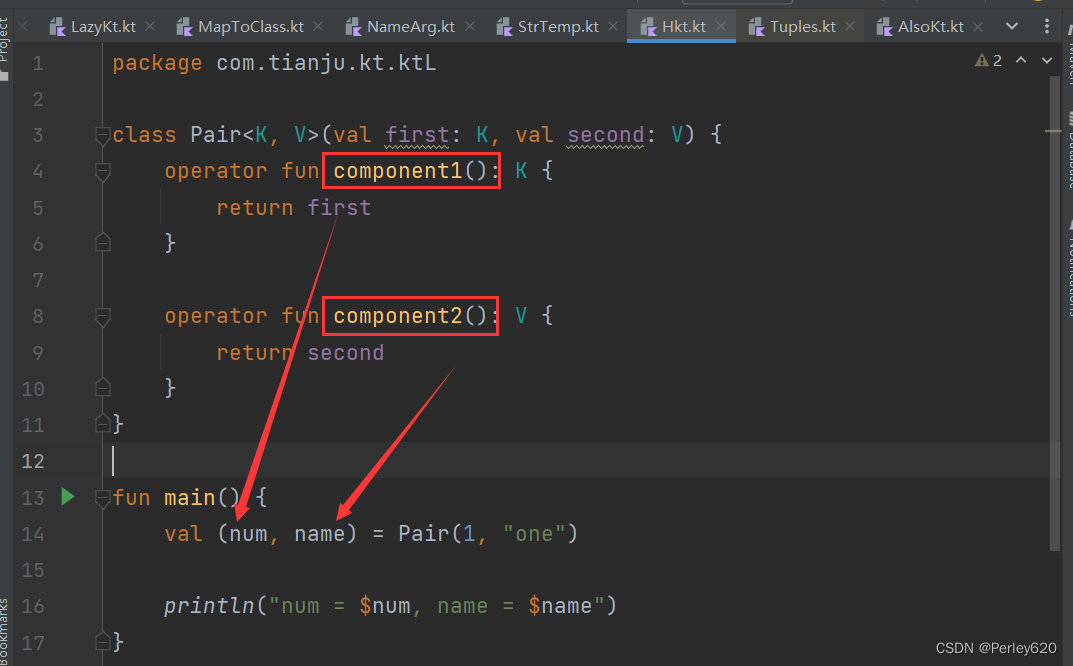
Kotlin学习——kt入门合集博客 kt里的委派模式Delegation kt里的特性
Kotlin 是一门现代但已成熟的编程语言,旨在让开发人员更幸福快乐。 它简洁、安全、可与 Java 及其他语言互操作,并提供了多种方式在多个平台间复用代码,以实现高效编程。 https://play.kotlinlang.org/byExample/01_introduction/02_Functio…...

数据挖掘 朴素贝叶斯
直入正题,直接看代码: 这是一段判断是不是藏话的代码 import numpy as np# 数据采集(定义函数加载数据集) def load_dataset():sent_list [[my, name, is, Devin],[you, are, stupid],[my, boyfriend, is, SB],[you, looks, ver…...

UI自动化测试工具有哪些优势?
UI自动化测试工具通过提高测试效率、覆盖率,减少测试时间和成本,以及支持持续集成等方式,为软件开发团队提供了一系列重要的优势,有助于提升软件质量和开发效率。 自动化执行:UI自动化测试工具可以模拟用户与应用程序的…...

【论文阅读笔记】InstructDiffusion: A Generalist Modeling Interface for Vision Tasks
【论文阅读笔记】StyleAvatar3D: Leveraging Image-Text Diffusion Models for High-Fidelity 3D Avatar Generation 论文阅读笔记论文信息引言动机挑战 方法结果 关键发现相关工作1. 视觉语言基础模型2. 视觉通用模型 方法/模型视觉任务的统一说明训练数据构建网络结构 实验设…...

笔记62:注意力汇聚 --- Nadaraya_Watson 核回归
本地笔记地址:D:\work_file\(4)DeepLearning_Learning\03_个人笔记\3.循环神经网络\第10章:动手学深度学习~注意力机制 a a a a a a a a a a a a a a a a...

给定一个n×n的方阵,本题要求计算该矩阵除副对角线、最后一列和最后一行以外的所有元素之和。
7-5 矩阵运算 分数 20 全屏浏览题目 切换布局 作者 C课程组 单位 浙江大学 给定一个nn的方阵,本题要求计算该矩阵除副对角线、最后一列和最后一行以外的所有元素之和。副对角线为从矩阵的右上角至左下角的连线。 输入格式: 输入第一行给出正整数n(…...

Go语言的学习笔记3——Go语言项目布局
Go 1.11 版本开始引入 go.mod 和 go.sum 以支持Go Module构建机制,而这种机制成为官方的依赖包管理方式。 现在Go可执行程序项目的典型布局如下所示: exe-layout ├── cmd/ │ ├── app1/ │ │ └── main.go │ └── app2/ │ └…...

70-76-堆、贪心算法
LeetCode 热题 100 文章目录 LeetCode 热题 100堆70. 中等-数组中的第K个最大元素71. 中等-前K个高频元素72. 困难-数据流中的中位数 贪心算法73. 简单-买卖股票的最佳时机74. 中等-跳跃游戏75. 中等-跳跃游戏II76. 中等-划分字母区间 本文存储我刷题的笔记。 堆 70. 中等-数组…...

Qt Network
Qt Network Qt Network为使用TCP/IP的应用程序编程提供了一组API。各种C++类处理诸如请求、cookies和通过HTTP发送数据之类的操作。 标题使用模块 使用Qt模块需要直接或通过其他依赖项链接到模块库。一些构建工具对此有专门的支持,包括CMake和qmake. 标题使用CMake构建 使…...
Win10电脑用U盘重装系统的步骤
在Win10电脑中,用户遇到了无法解决的系统问题,用户这时候就可以考虑重装Win10系统,这样即可轻松解决问题,从而满足自己的操作需求。接下来小编给大家详细介绍关于Win10电脑中用U盘重装系统的教程步骤。 准备工作 1. 一台正常联网可…...

安防视频监控/磁盘阵列/集中云存储平台EasyCVR设备录像保活不生效原因是什么?该如何解决?
安防视频监控/视频集中存储/云存储/磁盘阵列EasyCVR平台可拓展性强、视频能力灵活、部署轻快,可支持的主流标准协议有国标GB28181、RTSP/Onvif、RTMP等,以及支持厂家私有协议与SDK接入,包括海康Ehome、海大宇等设备的SDK等。平台既具备传统安…...
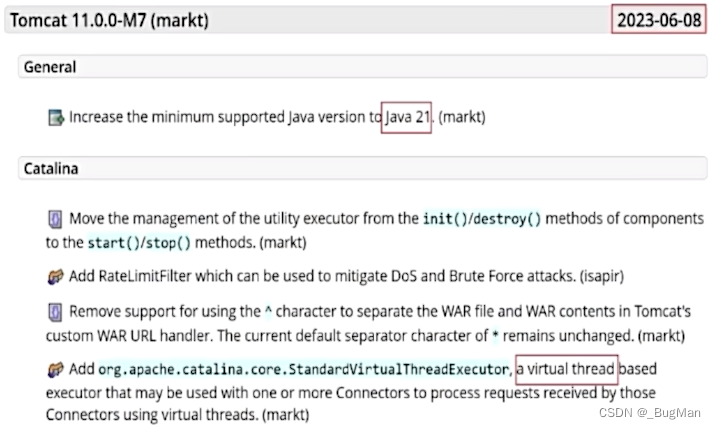
【JDK21】详解虚拟线程
目录 1.概述 2.虚拟线程是为了解决哪些问题 2.1.线程切换的巨大代价 2.2.哪些情况会造成线程的切换 2.3.线程资源是有限的 3.虚拟线程 4.适用场景 1.概述 你发任你发,我用JAVA8?JDK21可能要对这句话say no了。 现在Oracle JDK是每4个版本&#x…...
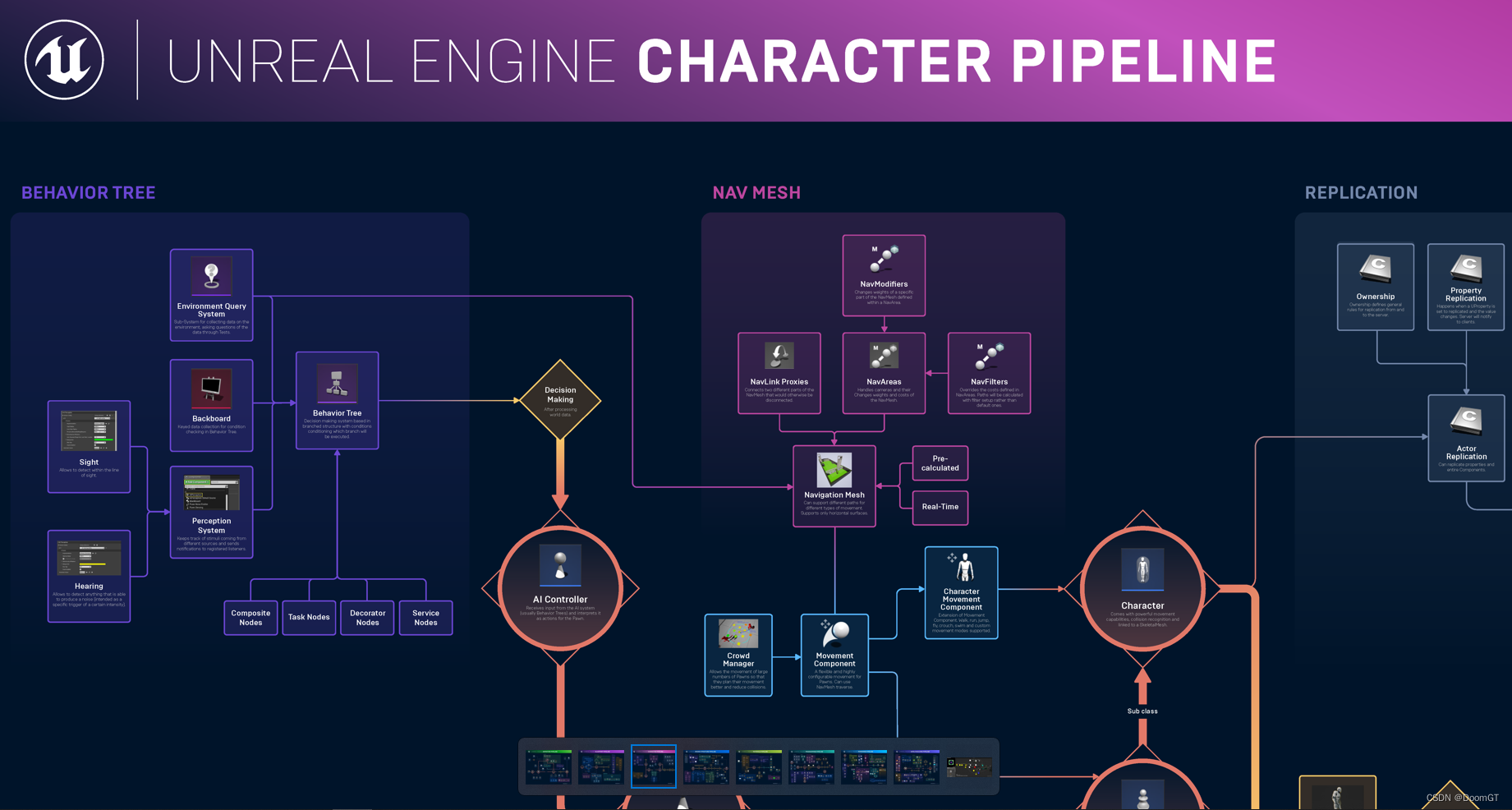
UE5 - 虚幻引擎各模块流程图
来自虚幻官方的一些资料,分享一下; 一些模块的流程图,比如动画模块: 或角色相关流程: 由于图片比较大,上传到了网络,可自取: 链接:https://pan.baidu.com/s/1BQ2KiuP08c…...
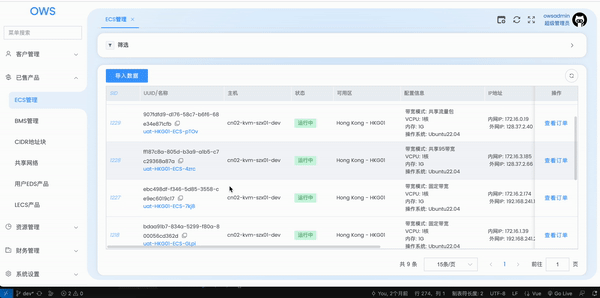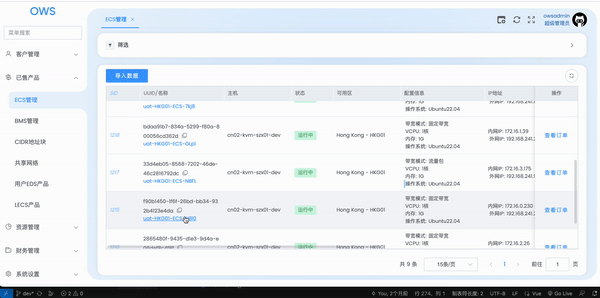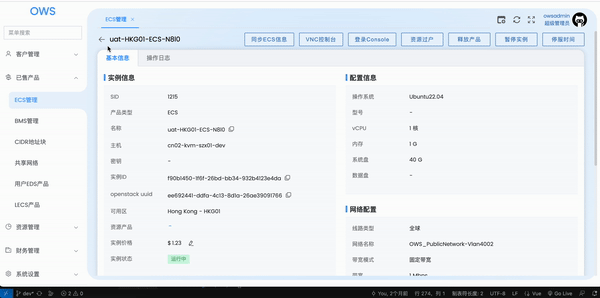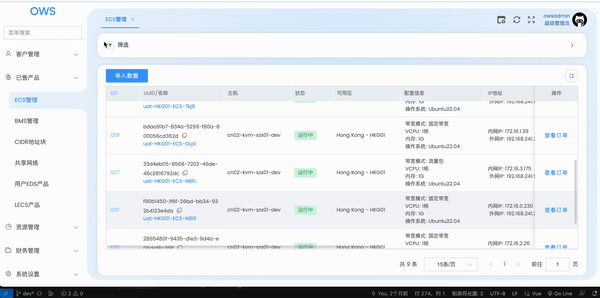
vue3实现element table缓存滚动条
背景 对于后台管理系统,数据的展示形式大多都是通过表格,常常会出现的一种场景,从表格跳到二级页面,再返回上一页时,需要缓存当前的页码和滚动条的位置,以为使用keep-alive就能实现这两种诉求,…...
)
flutter布局详解及代码示例(下)
布局 基本布局 GridView(二维滚动列表):比ListView多了一个方向的数据填充。ListBody(滚动列表):相比ListView,没有回收复用,简单易用。Table(表格布局)&am…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...
