【深度学习笔记】04 概率论基础
04 概率论基础
- 概率论公理
- 联合概率
- 条件概率
- 贝叶斯定理
- 边际化
- 独立性
- 期望和方差
- 模拟投掷骰子的概率随投掷次数增加的变化
概率论公理
概率(probability)可以被认为是将集合映射到真实值的函数。
在给定的样本空间 S \mathcal{S} S中,事件 A \mathcal{A} A的概率,
表示为 P ( A ) P(\mathcal{A}) P(A),满足以下属性:
- 对于任意事件 A \mathcal{A} A,其概率从不会是负数,即 P ( A ) ≥ 0 P(\mathcal{A}) \geq 0 P(A)≥0;
- 整个样本空间的概率为 1 1 1,即 P ( S ) = 1 P(\mathcal{S}) = 1 P(S)=1;
- 对于互斥(mutually exclusive)事件(对于所有 i ≠ j i \neq j i=j都有 A i ∩ A j = ∅ \mathcal{A}_i \cap \mathcal{A}_j = \emptyset Ai∩Aj=∅)的任意一个可数序列 A 1 , A 2 , … \mathcal{A}_1, \mathcal{A}_2, \ldots A1,A2,…,序列中任意一个事件发生的概率等于它们各自发生的概率之和,即 P ( ⋃ i = 1 ∞ A i ) = ∑ i = 1 ∞ P ( A i ) P(\bigcup_{i=1}^{\infty} \mathcal{A}_i) = \sum_{i=1}^{\infty} P(\mathcal{A}_i) P(⋃i=1∞Ai)=∑i=1∞P(Ai)。
联合概率
P ( A = a , B = b ) P(A=a,B=b) P(A=a,B=b)
给定任意值 a a a和 b b b,联合概率可以回答: A = a A=a A=a和 B = b B=b B=b同时满足的概率是多少?
对于任何 a a a和 b b b的取值, P ( A = a , B = b ) ≤ P ( A = a ) P(A = a, B=b) \leq P(A=a) P(A=a,B=b)≤P(A=a)。
条件概率
0 ≤ P ( A = a , B = b ) P ( A = a ) ≤ 1 0 \leq \frac{P(A=a, B=b)}{P(A=a)} \leq 1 0≤P(A=a)P(A=a,B=b)≤1。
我们称这个比率为条件概率(conditional probability),
并用 P ( B = b ∣ A = a ) P(B=b \mid A=a) P(B=b∣A=a)表示它:它是 B = b B=b B=b的概率,前提是 A = a A=a A=a已发生。
贝叶斯定理
根据乘法法则(multiplication rule )可得到 P ( A , B ) = P ( B ∣ A ) P ( A ) P(A, B) = P(B \mid A) P(A) P(A,B)=P(B∣A)P(A)。
根据对称性,可得到 P ( A , B ) = P ( A ∣ B ) P ( B ) P(A, B) = P(A \mid B) P(B) P(A,B)=P(A∣B)P(B)。
假设 P ( B ) > 0 P(B)>0 P(B)>0,求解其中一个条件变量,我们得到
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) . P(A \mid B) = \frac{P(B \mid A) P(A)}{P(B)}. P(A∣B)=P(B)P(B∣A)P(A).
其中 P ( A , B ) P(A, B) P(A,B)是一个联合分布(joint distribution),
P ( A ∣ B ) P(A \mid B) P(A∣B)是一个条件分布(conditional distribution)。
这种分布可以在给定值 A = a , B = b A = a, B=b A=a,B=b上进行求值。
边际化
为了能进行事件概率求和,需要求和法则(sum rule),
即 B B B的概率相当于计算 A A A的所有可能选择,并将所有选择的联合概率聚合在一起:
P ( B ) = ∑ A P ( A , B ) , P(B) = \sum_{A} P(A, B), P(B)=A∑P(A,B),
这也称为边际化(marginalization)。
边际化结果的概率或分布称为边际概率(marginal probability)
或边际分布(marginal distribution)。
独立性
如果两个随机变量 A A A和 B B B是独立的,意味着事件 A A A的发生跟 B B B事件的发生无关。
在这种情况下,通常将这一点表述为 A ⊥ B A \perp B A⊥B。
根据贝叶斯定理,马上就能同样得到 P ( A ∣ B ) = P ( A ) P(A \mid B) = P(A) P(A∣B)=P(A)。
在所有其他情况下,我们称 A A A和 B B B依赖。
由于 P ( A ∣ B ) = P ( A , B ) P ( B ) = P ( A ) P(A \mid B) = \frac{P(A, B)}{P(B)} = P(A) P(A∣B)=P(B)P(A,B)=P(A)等价于 P ( A , B ) = P ( A ) P ( B ) P(A, B) = P(A)P(B) P(A,B)=P(A)P(B),
因此两个随机变量是独立的,当且仅当两个随机变量的联合分布是其各自分布的乘积。
同样地,给定另一个随机变量 C C C时,两个随机变量 A A A和 B B B是条件独立的(conditionally independent),
当且仅当 P ( A , B ∣ C ) = P ( A ∣ C ) P ( B ∣ C ) P(A, B \mid C) = P(A \mid C)P(B \mid C) P(A,B∣C)=P(A∣C)P(B∣C)。
这个情况表示为 A ⊥ B ∣ C A \perp B \mid C A⊥B∣C。
期望和方差
一个随机变量 X X X的期望(expectation,或平均值(average))表示为
E [ X ] = ∑ x x P ( X = x ) . E[X] = \sum_{x} x P(X = x). E[X]=x∑xP(X=x).
当函数 f ( x ) f(x) f(x)的输入是从分布 P P P中抽取的随机变量时, f ( x ) f(x) f(x)的期望值为
E x ∼ P [ f ( x ) ] = ∑ x f ( x ) P ( x ) . E_{x \sim P}[f(x)] = \sum_x f(x) P(x). Ex∼P[f(x)]=x∑f(x)P(x).
在许多情况下,我们希望衡量随机变量 X X X与其期望值的偏置。这可以通过方差来量化
V a r [ X ] = E [ ( X − E [ X ] ) 2 ] = E [ X 2 ] − E [ X ] 2 . \mathrm{Var}[X] = E\left[(X - E[X])^2\right] = E[X^2] - E[X]^2. Var[X]=E[(X−E[X])2]=E[X2]−E[X]2.
方差的平方根被称为标准差(standard deviation)。
随机变量函数的方差衡量的是:当从该随机变量分布中采样不同值 x x x时,
函数值偏离该函数的期望的程度:
V a r [ f ( x ) ] = E [ ( f ( x ) − E [ f ( x ) ] ) 2 ] . \mathrm{Var}[f(x)] = E\left[\left(f(x) - E[f(x)]\right)^2\right]. Var[f(x)]=E[(f(x)−E[f(x)])2].
模拟投掷骰子的概率随投掷次数增加的变化
%matplotlib inline
import torch
from torch.distributions import multinomial
from d2l import torch as d2l
为了抽取像本,即掷骰子,我们只需为了抽取一个样本,
输出是另一个相同长度的向量:它在索引 i i i处的值是采样结果中 i i i出现的次数。
fair_probs = torch.ones([6]) / 6
multinomial.Multinomial(1, fair_probs).sample()
tensor([0., 1., 0., 0., 0., 0.])
使用PyTorch框架的函数同时抽取多个样本,得到我们想要的任意形状的独立样本数组
multinomial.Multinomial(10, fair_probs).sample()
tensor([3., 2., 0., 3., 1., 1.])
模拟1000次投掷,
然后统计1000次投掷后,每个数字被投中了多少次。
# 将结果存储为32位浮点数以进行除法
counts = multinomial.Multinomial(1000, fair_probs).sample()
counts / 1000 # 相对频率作为估计值
tensor([0.1650, 0.1650, 0.1720, 0.1750, 0.1610, 0.1620])
进行500组实验,每组抽取10个样本。
counts = multinomial.Multinomial(10, fair_probs).sample((500,))
cum_counts = counts.cumsum(dim=0)
estimates = cum_counts / cum_counts.sum(dim=1, keepdims=True)d2l.set_figsize((6, 4.5))
for i in range(6):d2l.plt.plot(estimates[:, i].numpy(),label=("P(die=" + str(i + 1) + ")"))
d2l.plt.axhline(y=0.167, color='black', linestyle='dashed')
d2l.plt.gca().set_xlabel('Groups of experiments')
d2l.plt.gca().set_ylabel('Estimated probability')
d2l.plt.legend();
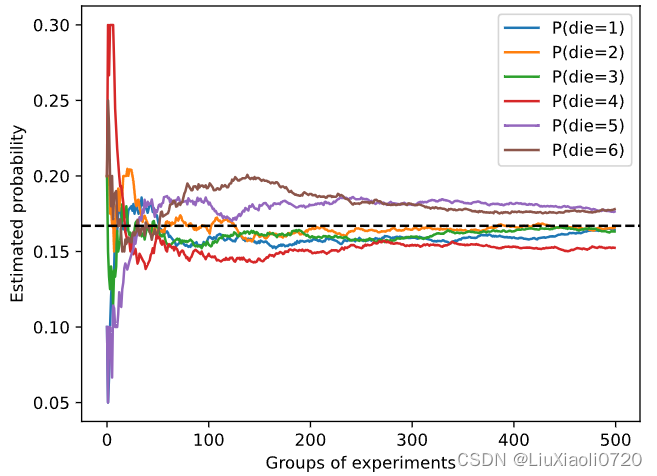
每条实线对应于骰子的6个值中的一个,并给出骰子在每组实验后出现值的估计概率。
当我们通过更多的实验获得更多的数据时,这 6 6 6条实体曲线向真实概率收敛。
相关文章:

【深度学习笔记】04 概率论基础
04 概率论基础 概率论公理联合概率条件概率贝叶斯定理边际化独立性期望和方差模拟投掷骰子的概率随投掷次数增加的变化 概率论公理 概率(probability)可以被认为是将集合映射到真实值的函数。 在给定的样本空间 S \mathcal{S} S中,事件 A \m…...

45.113.200.1搜索引擎蜘蛛抓取不到网站内容页面可能的原因
以下是搜索引擎蜘蛛抓取不到网站内容页面的一些主要原因总结: 网站的 robots.txt 文件中禁止了搜索引擎蜘蛛访问网站某些页面或目录,导致搜索引擎无法抓取到相关页面的内容。 网站的页面存在重定向或者跳转,搜索引擎蜘蛛无法直接抓取到需要的…...

VMware 系列:vSphere Client安装配置常见问题及解决方案
vSphere Client安装配置常见问题及解决方案 1.本地通过远程桌面复制文件或者文件夹到windows服务器时出错提示“未指定的错误”问题描述:原因分析:解决方案:方法 1方法 2方法 32.远程桌面连接出现身份验证错误要求的函数不受支持问题描述:原因分析:解决方案:3.Windows se…...
FLASK博客系列5——模板之从天而降
我们啰啰嗦嗦讲了4篇,都是在调接口,啥时候能看到漂亮的页面呢?别急,今天我们就来实现。 来我们先来实现一个简单的页面。不多说,上代码。 app.route(/) def index():user {username: clannadhh}return <html>&…...

6.一维数组——用冒泡法将10个整数由大到小排序
文章目录 前言一、题目描述 二、题目分析 三、解题 程序运行代码 前言 本系列为一维数组编程题,点滴成长,一起逆袭。 一、题目描述 用冒泡法将10个整数由大到小排序 二、题目分析 三、解题 程序运行代码 #include<stdio.h> int main() {int …...
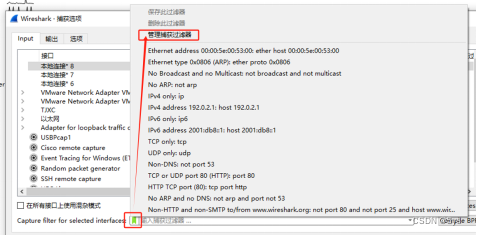
Wireshark的捕获过滤器
Wireshark的过滤器,顾名思义,作用是对数据包进行过滤处理。具体过滤器包括捕获过滤器和显示过滤器。本文对捕获过滤器进行分析。 捕获过滤器:当进行数据包捕获时,只有那些满足给定的包含/排除表达式的数据包会被捕获。 捕获过滤器…...

安陆FPGA调试中遇到的问题总结
参考链接:安陆FPGA踩坑填坑记录(梦里呓语回忆录)_fpga开发是个大坑-CSDN博客 上海安陆FPGA设置重上电启动速度_安路 fpga 加载时间-CSDN博客...

Springboot2+WebSocket
一、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dependency> 二、添加配置 新增配置文件 config/WebSocketConfig.java import org.springframewo…...

希尔伯特和包络变换
一、希尔伯特变换 Hilbert Transform,数学定义:在数学与信号处理的领域中,一个实值函数的希尔伯特变换是将信号x(t)与h(t)1/(πt)做卷积,以得到其希尔伯特变换。因此,希尔伯特变换结果可以理解为输入是x(t)的线性时不…...

国产Ai大模型和chtgpt3.5的比较
下面是针对国产大模型,腾讯混元,百度文心一言,阿里通义千问和chatgpt的比较,最基础的对一篇文章的单词书进行统计,只有文心一言和chatgpt回答差不多,阿里和腾讯差太多了...

机器学习ROC曲线中的阈值thresholds
在ROC(Receiver Operating Characteristic)曲线中,阈值(thresholds)是一个用于分类模型的概率或分数的截断值。ROC曲线的绘制涉及使用不同的阈值来计算真正例率(True Positive Rate,TPR…...

MySOL常见四种连接查询
1、内联接 (典型的联接运算,使用像 或 <> 之类的比较运算符)。包括相等联接和自然联接。 内联接使用比较运算符根据每个表共有的列的值匹配两个表中的行。例如,检索 students和courses表中学生标识号相同的所有行。 2、…...
数智融合 开启金融数据治理新时代
11月24日,由上海罗盘信息科技有限公司(罗盘科技)主办,北京酷克数据科技有限公司(酷克数据)支持协办的“博学近思 切问治理”数据治理分享会在上海成功举行。 本次会议深度聚焦金融行业数智化转型ÿ…...

数据结构——利用堆进行对数组的排序
今天文章的内容是关于我们如何利用堆的特性对我们的数组进行排序,还有就是我们的TopK的问题,这次我们放在的是文件种,我们放入一亿个数字,然后我们取出一亿个数字中最大的十个数,利用上章堆的问题进行解决。 首先就是我…...
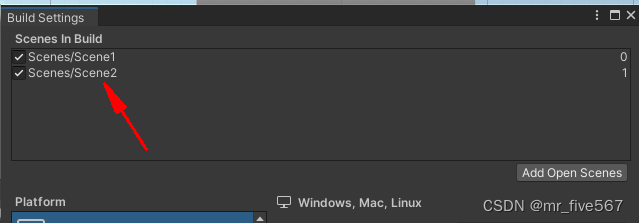
Unity 场景切换
Unity场景切换可使用以下方法: 1、SceneManager.LoadScene()方法: using UnityEngine.SceneManagement;// 切换到Scene2场景 SceneManager.LoadScene("Scene2"); 2、使用SceneManager.LoadSceneAsync()方法异步加载场景,异步加载…...

【PTA题目】7-12 N个数求和 分数 20
7-12 N个数求和 分数 20 全屏浏览题目 切换布局 作者 陈越 单位 浙江大学 本题的要求很简单,就是求N个数字的和。麻烦的是,这些数字是以有理数分子/分母的形式给出的,你输出的和也必须是有理数的形式。 输入格式: 输入第一行…...
智能AIGC写作系统ChatGPT系统源码+Midjourney绘画+支持GPT-4-Turbo模型+支持GPT-4图片对话
一、AI创作系统 SparkAi创作系统是基于ChatGPT进行开发的Ai智能问答系统和Midjourney绘画系统,支持OpenAI-GPT全模型国内AI全模型。本期针对源码系统整体测试下来非常完美,可以说SparkAi是目前国内一款的ChatGPT对接OpenAI软件系统。那么如何搭建部署AI…...

List转string 逗号分隔
List转string 逗号分隔 1、将list转化为逗号分割的字符串 String str String.join(",", list); String str StringUtils.json(list.toArray(), ","); 2、将逗号分隔的字符串转换为List List<String> list Arrays.asList(str.split("…...
手机文件怎么传到电脑?简单方法分享!
将手机文件传输到电脑可以将其备份,以防数据丢失或意外情况发生。并且电脑具有更强大的处理能力,可以将文件进行编辑、修改、转换等操作,大大提高了工作效率。那么,手机文件怎么传到电脑?本文将为大家提供简单易懂的解…...
计算机基础知识59
MySQL的卸载流程 1、先停止MySQL服务:右键“此电脑”,选择“管理”,之后选择“服务和应用程序”--“服务”,在服务中找到“MySQL”,右键选择“停止”。 2、找到“控制面板”--“程序和功能”,找到MySQL&…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...
