【每日一题】子数组的最小值之和
文章目录
- Tag
- 题目来源
- 题目解读
- 解题思路
- 方法一:贡献法+单调栈
- 写在最后
Tag
【贡献法】【单调栈】【数组】【2023-11-27】
题目来源
907. 子数组的最小值之和

题目解读
计算整数数组的连续子数组中最小值的和。
解题思路
本题朴素的解决思想是求出所有的连续子数组,遍历每一个子数组然后将每一个子数组的最小和加和得到结果,但是该方法时间复杂度过高。现在介绍一种时间复杂度较优的方法——贡献法。
方法一:贡献法+单调栈
我们从数组中的每一个元素作为连续子数组中的最小值这一角度考虑,比如在数组 arr = [3, 1, 2, 4] 中,考虑 1 作为子数组中的最小值的情况,有这些子数组满足 1 是子数组中的最小值 :
[ 3 , 1 ] , [ 3 , 1 , 2 ] , [ 3 , 1 , 2 , 4 ] , [ 1 ] , [ 1 , 2 ] , [ 1 , 2 , 4 ] [3, 1], [3, 1, 2], [3, 1, 2, 4], [1], [1, 2], [1, 2, 4] [3,1],[3,1,2],[3,1,2,4],[1],[1,2],[1,2,4]
共计6个。利用乘法原理有:
6 = ( i − a ) ∗ ( b − i ) = 2 ∗ 3 6 = (i - a) * (b - i) = 2 * 3 6=(i−a)∗(b−i)=2∗3
其中,a 表示在 arr 数组中 1 左侧比 1 小的第一个元素的下标,默认值为 -1,此时 a = -1;
b 表示在 arr 数组中 1 右侧比 1 小的第一个元素的下标,默认值为 n,此时 b = n。
以上是 arr 数组中无重复元素的情况,我们只需要找出元素 arr[i] 左侧第一个比它小的元素下标 a、元素 arr[i] 右侧第一个比它小的元素下标 b,利用乘法原理即可得到 arr[i] 作为连续子数组的最小值时的答案,我们遍历数组中的所有元素,计算作为连续子数组的最小值时的答案,将所有答案进行加和得到最终的答案,时间复杂度为 O ( n ) O(n) O(n)。
一般的情况,若是 arr 数组中有重复元素出现会怎么样呢?此处参考 贡献法+单调栈+三种实现版本(附题单)Python/Java/C++/Go。
如果 arr 有重复元素,例如 arr=[1, 2, 4, 2, 3, 1],其中第一个 2 和第二个 2 对应的边界都是开区间 (0,5),子数组 [2, 4, 2, 3] 都包含这两个 2,这样在计算答案时就会重复统计同一个子数组,算出错误的结果。
为避免重复统计,可以修改边界的定义,把右边界改为「找小于或等于 arr[i] 的数的下标」,那么:
- 第一个
2对应的边界是(0,3),子数组需要在(0,3)范围内且包含下标1; - 第二个
2对应的边界是(0,5),子数组需要在(0,5)范围内且包含下标3。
这样以第一个2为最小值的子数组,就不会「越界」包含第二个2了,从而解决了重复统计子数组的问题。
实现代码
#define MOD 1000000007
class Solution {
public:int sumSubarrayMins(vector<int>& arr) {int n = arr.size();vector<int> lLessIdx(n, -1);vector<int> rLessAndEquIdx(n, n);// 用单调栈更新 lLessIdxint i;stack<int> stk;// [3, 1, 2, 4]for(i = 0; i < n; ++i) {while(!stk.empty() && arr[stk.top()] >= arr[i]) {stk.pop();}if (!stk.empty()) lLessIdx[i] = stk.top();stk.push(i);} // 用单调栈更新 rLessAndEquIdxwhile (!stk.empty()) stk.pop();for(i = n-1; i >= 0; --i) {while(!stk.empty() && arr[stk.top()] > arr[i]) {stk.pop();}if (!stk.empty()) rLessAndEquIdx[i] = stk.top();stk.push(i);}long ans = 0;for(i = 0; i < n; ++i) {int a = lLessIdx[i], b = rLessAndEquIdx[i];ans += (long)((i - a) * (b - i)) % MOD * arr[i] % MOD; // 乘法原理ans %= MOD;}return (int)ans;}
};
复杂度分析
时间复杂度: O ( n ) O(n) O(n), n n n 是数组 arr 的长度。
空间复杂度: O ( n ) O(n) O(n)。
写在最后
如果文章内容有任何错误或者您对文章有任何疑问,欢迎私信博主或者在评论区指出 💬💬💬。
如果大家有更优的时间、空间复杂度方法,欢迎评论区交流。
最后,感谢您的阅读,如果感到有所收获的话可以给博主点一个 👍 哦。
相关文章:

【每日一题】子数组的最小值之和
文章目录 Tag题目来源题目解读解题思路方法一:贡献法单调栈 写在最后 Tag 【贡献法】【单调栈】【数组】【2023-11-27】 题目来源 907. 子数组的最小值之和 题目解读 计算整数数组的连续子数组中最小值的和。 解题思路 本题朴素的解决思想是求出所有的连续子数组…...

【docker】docker总结
一、Docker简介 Docker是开源应用容器引擎,轻量级容器技术。基于Go语言,并遵循Apache2.0协议开源Docker可以让开发者打包他们的应用以及依赖包到一个轻量级、可移植的容器中,然后发布到任何流行的Linux系统上,也可以实现虚拟化容…...

[英语学习][3][Word Power Made Easy]的精读与翻译优化
[序言] 这次翻译校验, 难度有点大, 原版中英翻译已出现了严重地偏差. 昨晚11点开始阅读如下段落, 花费了1个小时也没有理解原作者的核心表达, 索性睡觉了. 今早学习完朗文单词之后, 9点半开始继续揣摩. 竟然弄到了中午11点30, 终于明白原作者要表达的意思了. 废话不多说&#x…...

使用UIActivityViewController分享图片,没有preview
以前都是用第三方sdk来分享的,最近使用官方的UIActivityViewController来做分享,结果分享图片的时候preview不了分享的图片。 自定义一个继承UIActivityItemProvider的类。关于分享的内容自定义可以自己实现UIActivityItemSource这个协议。首先看看协议的…...
linux安装终端连接工具Tabby
参考:https://zhuanlan.zhihu.com/p/645787655...
)
Linux telnet命令详解:通过TCP/IP网络连接与管理远程机器(附实例教程和注意事项)
Linux telnet命令介绍 telnet命令,全称为teletype network,是一个使用telnet网络协议来连接并管理远程机器的命令。它通过TCP/IP网络使用端口23来建立连接,并提供了一种使用命令行界面(CLI)管理远程系统的方式。虽然t…...
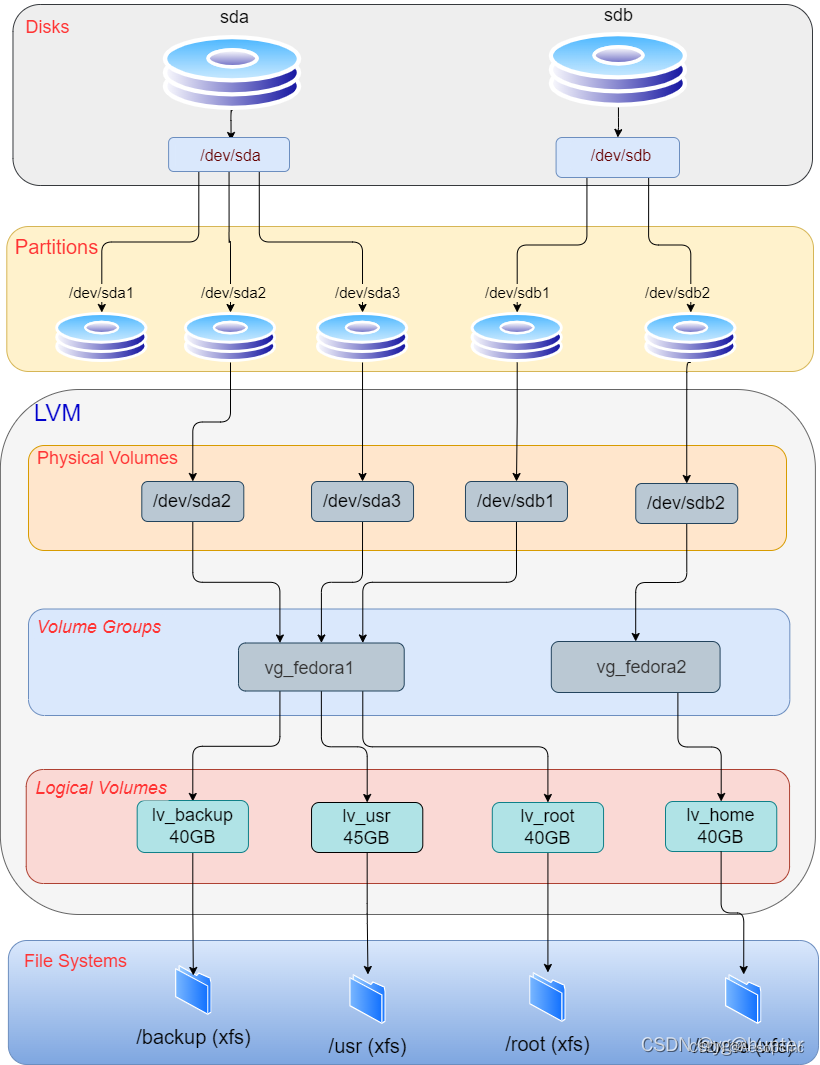
linux 磁盘管理、分区管理常用命令
文章目录 基础命令挂载新硬盘/分区添加内存交换分区swaplvm分区管理模式 基础命令 查看目录文件大小 du -sh /backup du -sh /backup/* du -sh *查看磁盘挂载信息 df -lhT查看某个目录挂载在哪个分区,以及分区的磁盘使用情况 df [目录] #例如:df /ho…...
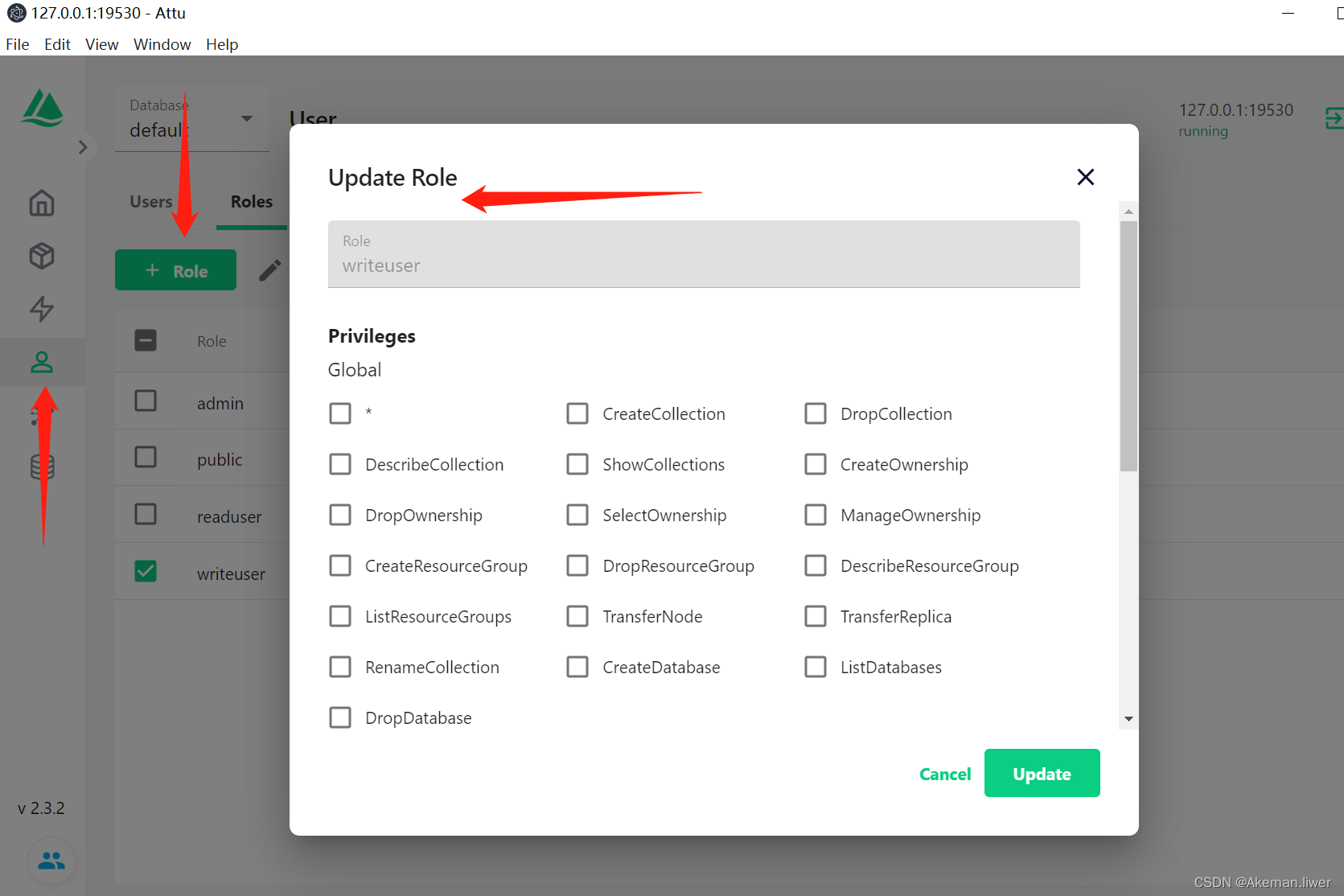
Milvus入门手册1.0
一、window环境搭建(单机) 1、docker安装 略 2、milvus安装 参考文档:https://milvus.io/docs/install_standalone-docker.md tips: (1)compose.yaml下载比较慢,可以在网络上找一份。 (2&…...

PCL 计算两点云之间的最小距离
目录 一、 算法原理二、 代码实现三、 结果展示四、 相关链接本文由CSDN点云侠原创,原文链接。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的爬虫与GPT。 一、 算法原理 pcl::registration::CorrespondenceEstimation是确定目标和查询点集(或特征)之间对应关…...

基于YOLOv5的视频计数 — 汽车计数实现
在视频中计数对象可能看起来有挑战性,但借助Python和OpenCV的强大功能,变得令人意外地易于实现。在本文中,我们将探讨如何使用YOLO(You Only Look Once)目标检测模型在视频流或文件中计数对象。我们将该过程分解为简单…...
jetson nano 串口通信
目录 1.UART通信介绍 2.电脑端准备工作 2.1 安装串口调试助手 2.2 硬件接线 3.Jetson Nano端准备工作 3.1安装库文件 3.2修改主板上电启动串口权限 4.示例程序-发送及接收 4.1 开启串口调试助手 4.2 导入示例程序 4.3 执行程序 4.4 查看效果 4.4.1 串口调试端 4.4…...

Vue基础入门(三):Vue3的使用
Vue3的使用 一、首页案例修改 修改首页的信息:是在之前介绍的HelloWorld.vue文件中进行内容的修改。 页面展示效果: 此时就看到了我们新添加的文字了! 同样的我们开发代码的时候只需要修改了项目中的内容然后保存就会自动刷新的浏览器&…...

基于M估计样本一致性算法的点云平面拟合
平面拟合 1、算法简介2、参考文献3、实现效果4、相关代码 1、算法简介 RANSAC 是在给定模型和距离阈值 T T T的情况下,通过寻找最小代价 C C C来确定内点数据并拟合模型。如式(1)所示的代价函数,当点到模型的距离 e e e小于阈值 T…...

【VRTK】【VR开发】【Unity】8-可交互对象
课程配套学习资源下载 https://download.csdn.net/download/weixin_41697242/88485426?spm=1001.2014.3001.5503 【概述】 之前我们只是用了一个简单方块作为可交互对象。其实可交互对象可以有许多细节设置,包括具体抓握物体的哪个点,指定抓握的方向,指定Secondary Acti…...

Huggingface 超详细介绍
Hugging face 起初是一家总部位于纽约的聊天机器人初创服务商,他们本来打算创业做聊天机器人,然后在github上开源了一个Transformers库,虽然聊天机器人业务没搞起来,但是他们的这个库在机器学习社区迅速大火起来。目前已经共享了超…...
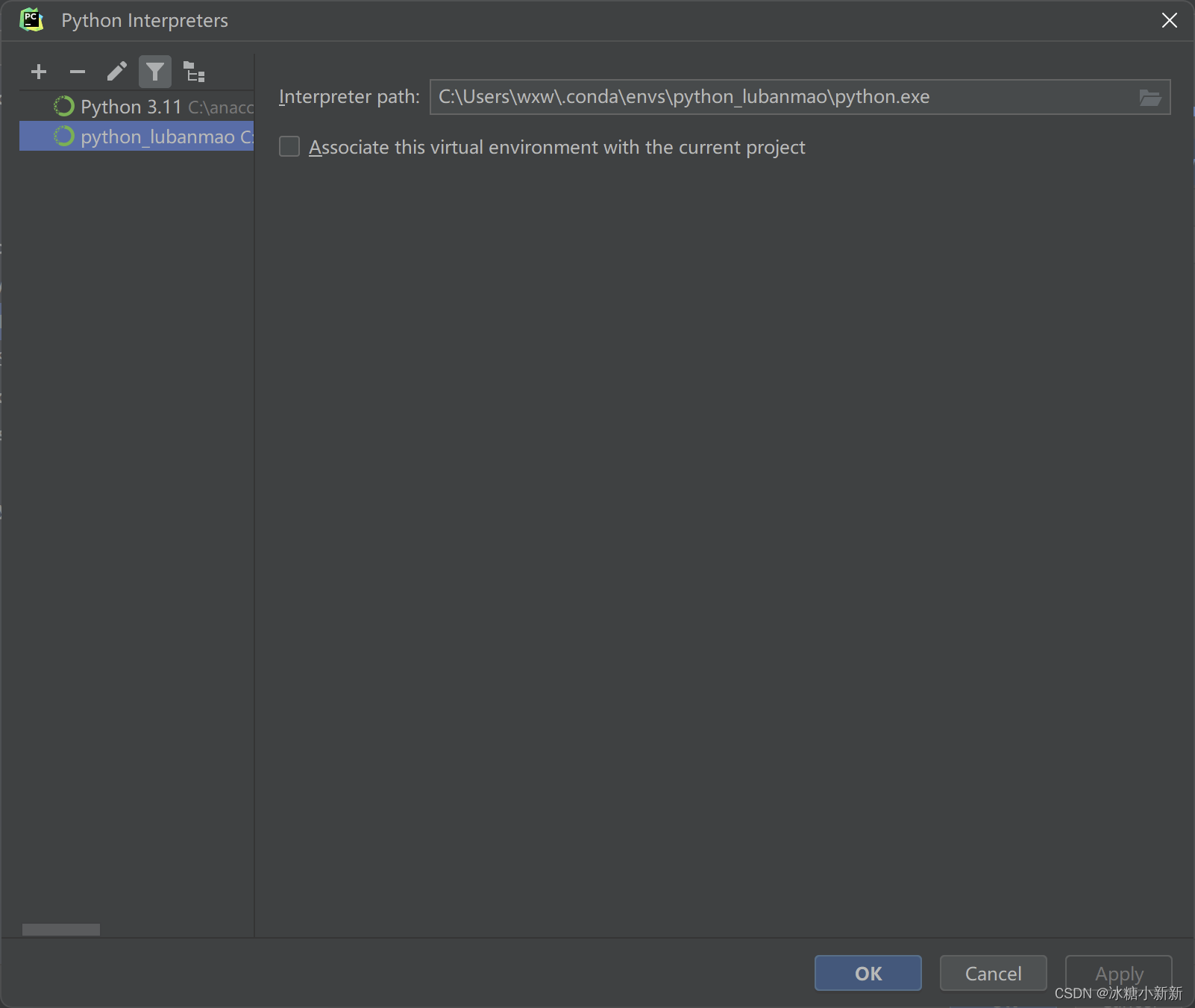
pycharm 怎么切换Anaconda简单粗暴
(1)创建一个环境 (2)选择一下自己conda的安装路径中conba.exe (3)选择存在的环境,一般会自动检测到conda创建有哪些环境,导入就行...

笔记二十二、使用路由state进行传递参数
22.1 父组件设置state路由参数 <NavLink toclassify state{{param_C: this.state.name, param_D: this.state.age}} className{this.activeStyle}>classify</NavLink> 父组件 Home/index.jsx import React from "react"; import {NavLink, Outlet} from…...

2023 OI 总结
2023 O I 2023 \space OI 2023 OI ここは总 • 结です ここは总\space• \space结です ここは总 • 结です 我也不知道要写些什么,就随便写了 csp/s第一题10min出ac思路,结果写炸了qwq,被旁边的大哥影响稍微有点大,没调完第一题…...

ESP32-Web-Server编程-HTML 基础
ESP32-Web-Server编程-HTML 基础 概述 HTML(HyperText Markup Language) 是用来描述网页的一种语言。其相关内容存储在前端代码的 .html 文件中。 当浏览器向 web 服务器请求网页时,一个 HTML 文件被发送给浏览器,浏览器解释该文件的内容,…...

【docker】docker安装与优化
目录 一、安装Docker 1、关闭防火墙 2、安装依赖包 3、设置阿里云镜像源 4、安装Docker-CE社区版并设置为开机自启动 5、查看Docker信息 二、设置镜像加速 1、申请加速地址 2、实现加速操作 三、网络优化 1、如何网络优化 2、具体操作 四、docker-server端配置文件…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...
