acwing算法基础之数学知识--Nim游戏和集合Nim游戏
目录
- 1 基础知识
- 2 模板
- 3 工程化
1 基础知识
(一)
Nim游戏: n n n堆物品,每堆有 a i a_i ai个,两个玩家轮流取走任意一堆的任意个物品,但不能不取。取走最后一个物品的人获胜。
结论:如果这n个数异或之和为0,则先手必败,否则先手必胜。
代码表示为,
#include <iostream>using namespace std;int main() {int n;cin >> n;int res = 0;while (n--) {int x;cin >> x;res = res ^ x;}if (res) puts("Yes");else puts("No");return 0;
}
(二)
集合Nim游戏:在Nim游戏的基础上,对每次取走的石子做了限制,每次取走的石子数必须在集合 S S S内。判断是否先手必胜。
抽象建模为,
有向图游戏和SG函数:在一个有向无环图中,只有一个起点,上面有一个棋子,两个玩家轮流沿有向边推动棋子,不能走的玩家判负。
定义mex函数的值为,不属于集合S中的最小非负整数,即:
m e x ( S ) = m i n { x } ( x ∉ S , x ∈ N ) mex(S)=min\{x\} \ (x\notin S, x\in N) mex(S)=min{x} (x∈/S,x∈N)
例如mex({0,2,3}) = 1, mex({1,2}) = 0。
对于状态 x x x和它的所有 k k k个后继状态 y 1 , y 2 , ⋯ , y k y_1,y_2,\cdots,y_k y1,y2,⋯,yk,定义SG函数:
S G ( x ) = m e x { S G ( y 1 ) , S G ( y 2 ) , ⋯ , S G ( y k ) } SG(x)=mex\{SG(y_1), SG(y_2), \cdots, SG(y_k)\} SG(x)=mex{SG(y1),SG(y2),⋯,SG(yk)}
而对于由n个有向图组成的组合游戏,设它们的起点分别为 s 1 , s 2 , ⋯ , s n s_1,s_2,\cdots,s_n s1,s2,⋯,sn,则有定理:当且仅当这 n n n个数 S G ( s 1 ) , S G ( s 2 ) , ⋯ , S G ( s n ) SG(s_1),SG(s_2),\cdots,SG(s_n) SG(s1),SG(s2),⋯,SG(sn)的异或和不为0时,这个游戏是先手必胜的,否则,是先手必败的。
C++代码如下,
#include <iostream>
#include <unordered_set>
#include <cstring>using namespace std;const int N = 110, M = 1e4 +10;
int n, m;
int s[N]; //每次可以取的石子数目
int f[M]; //这堆有x个石子,求sg[x]的值int sg(int x) {if (f[x] != -1) return f[x];unordered_set<int> S;//x能走到的结点的sg函数值for (int i = 0; i < n; ++i) {if (x - s[i] >= 0) S.insert(sg(x-s[i]));}for (int i = 0; ; ++i) {if (S.count(i) == 0) {f[x] = i;break;}}return f[x];
}int main() {cin >> n;for (int i = 0; i < n; ++i) cin >> s[i];int res = 0;memset(f, -1, sizeof f);cin >> m;while (m--) {int x;cin >> x;res ^= sg(x);}if (res) puts("Yes");else puts("No");return 0;
}
2 模板
暂无。。。
3 工程化
题目1:拆分Nim游戏,取走一堆,放回两堆规模更小的石子。
解题思路:重点在于如何确认某一堆的sg值,这样考虑遍历两堆规模更小的石子,就是它的下一步状态,求得它们的sg值,进行mex操作,即可得到这堆石子的sg值。
C++代码如下,
#include <iostream>
#include <unordered_set>
#include <cstring>using namespace std;const int N = 110;int n;
int f[N]; //sg值int sg(int x) {if (f[x] != -1) return f[x];//x可以走到的状态的sg值unordered_set<int> S;for (int i = 0; i < x; ++i) {for (int j = 0; j <= i; ++j) {S.insert(sg(i) ^ sg(j));}}//mex操作for (int i = 0; ; ++i) {if (!S.count(i)) {return f[x] = i;}}
}int main() {memset(f, -1, sizeof f);cin >> n;int res = 0;for (int i = 0; i < n; ++i) {int x;cin >> x;res ^= sg(x);}if (res) puts("Yes");else puts("No");return 0;
}
相关文章:

acwing算法基础之数学知识--Nim游戏和集合Nim游戏
目录 1 基础知识2 模板3 工程化 1 基础知识 (一) Nim游戏: n n n堆物品,每堆有 a i a_i ai个,两个玩家轮流取走任意一堆的任意个物品,但不能不取。取走最后一个物品的人获胜。 结论:如果这n…...

大数据Doris(二十八):Routine Load查看和修改作业
文章目录 Routine Load查看和修改作业 一、查看导入作业状态...
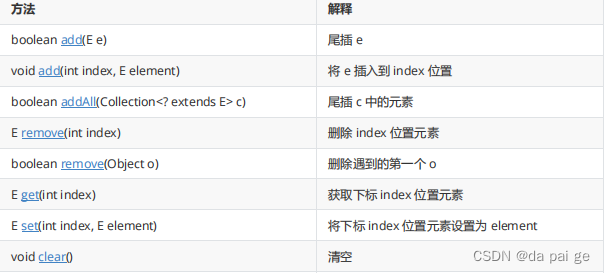
顺序表总结
📑打牌 : da pai ge的个人主页 🌤️个人专栏 : da pai ge的博客专栏 ☁️宝剑锋从磨砺出,梅花香自苦寒来 目录 🌤️arraylist的简…...
flutter 文本不随系统设置而改变大小[最全的整理]
文本不随系统设置而改变大小[四] 前言方案十九:使用LayoutBuilder和RichText方案二十:使用Transform.scale方案二十一:使用自定义文本缩放因子方案二十二:使用SingleChildScrollView方案二十三:使用FittedBox方案二十四…...
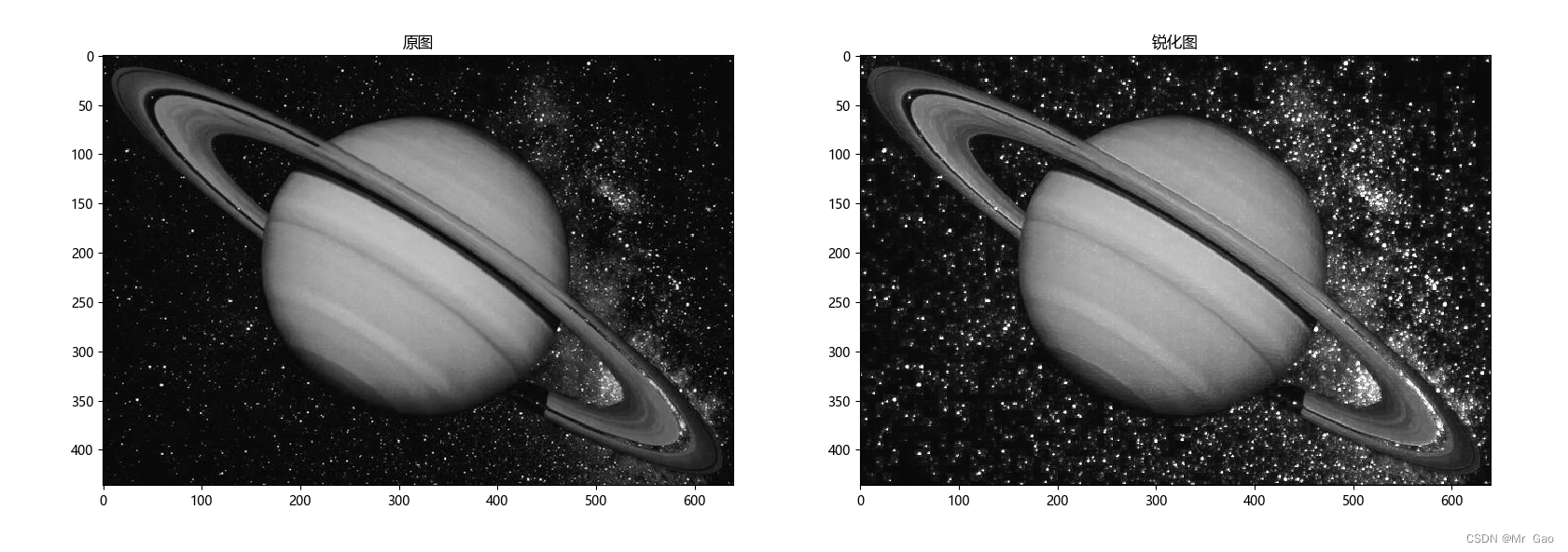
python -opencv 图像锐化
python -opencv 图像锐化 图像锐化其实,是一种增强图片对比度的技术,我们可以通过计算图像的导数,把导数绝对值数值大于零的数值加回原图像,通过这种方法,可以增强图像的对比度。 实现代码如下: import c…...
数字电源为什么一般用DSP控制,而不能用普通的单片机?
数字电源为什么一般用DSP控制,而不能用普通的单片机? 首先你要清楚,数字电源需要一个芯片具备什么功能? 1 能发PWM波 ,并且具备保护关断功能; 电源对PWM发波 要求很高,精度要ns级甚至ps级的&…...

个人投资白银收益怎么样?
个人投资白银是可以带来丰厚的收益,但收益的具体情况取决于多种因素。以下是一些明确的答案和举例,帮助投资者更好地理解个人投资白银的收益情况。 白银市场的价格波动是决定投资收益的主要因素之一,白银价格受全球经济形势、地缘局势风险、…...

代码随想录算法训练营 ---第四十五天
前言: 昨天的题做过之后,今天的题基本上都很简单,但是要注重一下细节。 第一题: 简介: 动态规划五部曲: 1.确定dp数组的含义 dp[i]:爬到有i个台阶的楼顶,有dp[i]种方法 2.确定dp…...
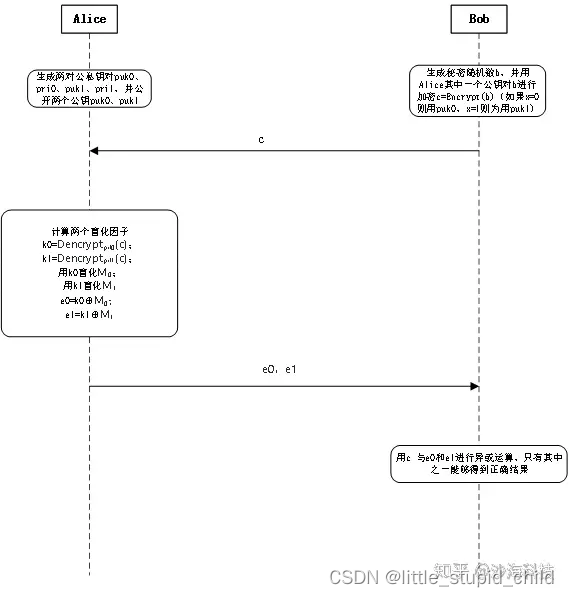
【密码学】【多方安全计算】不经意传输(Oblivious Transfer,OT)
文章目录 不经意传输(oblivious transfer)定义不经意传输的实例(1 out 2,二选一不经意传输)基于RSA的1 out 2 不经意传输疑问 不经意传输(oblivious transfer)定义 不经意传输(obli…...

STL常用算法-C++
概述: 算法主要是由头文件 <algorithm> <functional> <numeric> 组成。<algorithm> 是所有 STL 头文件中最大的一个,范围涉及是比较、交换、查找、遍历操作、复制、修改等等。<functional> 定义了一些模板类,…...

一、Lua基础
文章目录 一、Lua是什么二、Lua特性(一)轻量级(二)可扩展(三)其它特性 三、Lua安装四、Lua应用 看到评论说,C让我见识了语言的严谨与缜密,lua让我见识到了语言的精巧与创新ÿ…...

vue3 webSocket 封装及使用
vue3 webSocket 封装及使用 封装 import { ref, onUnmounted } from vue; interface SocketOptions {heartbeatInterval?: number;reconnectInterval?: number;maxReconnectAttempts?: number; }class Socket {url: string;ws: WebSocket | null null;opts: SocketOption…...
)
记录vscode常用插件集合(extensions)
名称用处Chinese (Simplified) (简体中文) Language Pack for Visual Studio Code适用于 VS Code 的中文(简体)语言包Dev ContainersVisual Studio代码开发容器ES7 React/Redux/GraphQL/React-Native snippetsES7 React/Redux/GraphQL/Rect Native代码段…...

正则表达式详解
一、正则表达式概述 正则表达式是一组由字母和符号组成的特殊文本,它可以用来从文本中找出满足你想要的格式的句子。通俗的讲就是按照某种规则去匹配符合条件的字符串 一个正则表达式是一种从左到右匹配主体字符串的模式。 “Regular expression”这个词比较拗口&a…...

【限时免费】20天拿下华为OD笔试之【双指针】2023Q1A-两数之和绝对值最小【欧弟算法】全网注释最详细分类最全的华为OD真题题解
文章目录 题目描述与示例题目描述输入输出示例一输入输出说明 解题思路代码解法一pythonjavacpp 解法二pythonjavacpp 时空复杂度 华为OD算法/大厂面试高频题算法练习冲刺训练 题目描述与示例 题目描述 给定一个整数数组nums,请你在该数组中找出两个数,…...

expect脚本在自动化部署中的具体应用案例
#expect脚本在自动化部署中的具体应用 expect脚本是一个非常好的交互式应用脚本,在自动化部署中,可以使用这个脚本来实现全自动的自动化部署。下面是一些具体的应用案例。 场景一:自动安装mysql 可以使用expect脚本来实现mysql自动安装&…...
【Java+SQL Server】前后端连接小白教程
目录 📋 流程总览 ⛳️【SQL Server】数据库操作 1. 新建数据库text 2. 新建表 3. 编辑表 ⛳️【IntelliJ IDEA】操作 1. 导入jar包 2. 运行显示错误 📋 流程总览 ⛳️【SQL Server】数据库操作 打开SQL Server数据库-->sa登录-->新建数据库…...
Xilinx Zynq-7000系列FPGA多路视频处理:图像缩放+视频拼接显示,提供工程源码和技术支持
目录 1、前言免责声明 2、相关方案推荐FPGA图像处理方案FPGA图像缩放方案FPGA视频拼接叠加融合方案推荐 3、设计思路详解HLS 图像缩放介绍Video Mixer介绍 4、vivado工程介绍PL 端 FPGA 逻辑设计PS 端 SDK 软件设计 5、工程移植说明vivado版本不一致处理FPGA型号不一致处理其他…...

Web语言基础课程期末代做
《Web语言基础》课程期末考核要求综合运用课程所学知识,使用VS和SQL及相关开发工具,结合DIVCSS等前端设计技术,完成一个具备新闻发布和考试功能的动态系统,要求包括但不限于:用户注册、登录功能、新闻展示功能、后台数…...

Scanner常用知识点
在Java中,Scanner类是用于读取用户输入的工具类,可以从多种输入源读取数据,如标准输入流、文件或字符串。以下是一些Scanner类的常用知识点: Scanner的初始化:在使用Scanner类之前,需要先将其导入到你的Ja…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...
