【追求卓越04】数据结构--栈与队列
引导
今天我们开始学习栈与队列的内容,我觉得栈并不难,所以篇幅也就不会那么多了。在虚拟空间中,栈是用户空间中的一种数据结构,它主要用于保存局部变量。那么问题来了,为什么用栈来保存局部变量,不用别的数据结构呢?堆,数组,链表不可以吗?
栈
我们知道栈的特点就是先进后出,后进先出。其实,我们可以这样定义,满足先进后出,后进先出操作特性的就是栈。因此栈没有固定的存储形式,比如数据是需要存储地址连续,链表存储地址可以不连续。栈可以用数组或链表都可以实现,只要它满足先进后出,后进先出操作特性即可。
因此栈就是一个操作受限(只能从一端压栈,出栈)的线性表。
栈的复杂度
栈的操作只有入栈和出栈,并且只涉及到栈顶的元素。所以它的复杂度都为O(1)。如图:
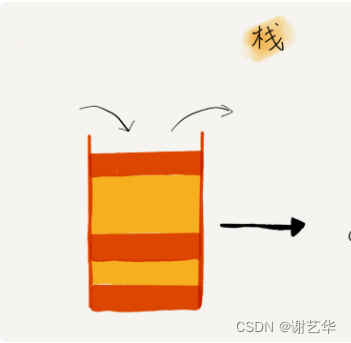
栈的应用
特定的数据结构是对特定场景的抽象。那么有些问题用栈来处理肯定会比较方便。
栈在表达式中的使用
在《程序语言设计基础》中有关于表达式知识点:比如一个3+5*8-6的表达式,你会怎么设计,让计算机去识别,计算呢?记得以前写过类似的程序,现在想想还有很多的优化空间。
在表达式中,有中缀表达式,前缀表达式,后缀表达式3种。它们的分析方式也不相同。有兴趣的可以去了解一下我的另一篇文章【献给过去的自己】栈实现计算器(C语言)-CSDN博客。
栈在函数调用中的应用
正如我们在开头引入的话题,为什么局部变量要保存在栈中?这里有几点需要解释:
- 局部变量保存在栈中,这个栈是内存中实际存在的栈,是真实的物理区。而我们全文所介绍的栈是一个数据结构,是抽象的。要区分开两个栈。
- 内存中的栈因为它的操作特性符合栈数据结构的特点,所以称为栈区。栈区主要存储运行方法的形参、局部变量、返回值。由系统自动分配和回收。
那么我们为什么要将局部变量保存在栈区呢?
其实我们并不是必须要使用栈结构,使用数组和链表也是可以的。可能稍微会麻烦点。函数之间调用,变化的主要是作用域及生命周期。
- 当A函数进入B函数,就不能再访问A函数中的局部变量了。
- B函数返回A函数之后,B函数中的局部变量就需要释放。
针对作用域和生面周期变化的,我觉得栈可以很好的实现。进入一个函数时,在栈中记录入口(作用域界限),之后进行压栈操作,在该函数内部只能访问界限以内的数据。当退出函数时,将入口以内的数据直接释放。
队列
队列和栈都是抽象的数据结构,是一个操作受限的线性表。它的特点就是先进先出(FIFO)。 它的操作又入队(将一个数据放到队尾)和出队(从队列头部取出一个数据)。和栈相似,如图:
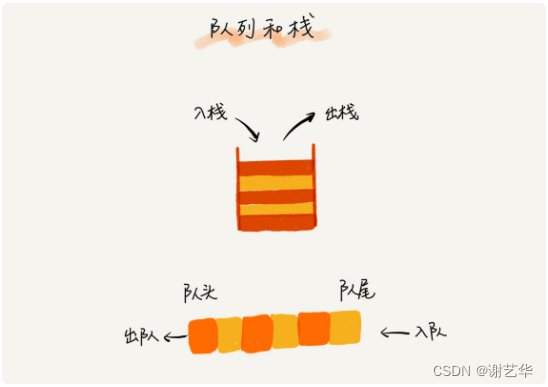
顺序队列
队列和栈一样,都能用数组和链表来实现。用数组实现就是顺序队列,用链表实现就是链式队列。我这里就简单用C语言实现一个顺序队列。
| queue_len = 100 |
该实现方式,出队和入队操作的复杂度都是O(1)。
循环队列
在上面的队列中,当tail等于队列长度时,就需要进行数据搬移。循环队列就是省去了这个操作。循环队列的难点就在于如何确定队列满和队列空
- 队列满:(tail+1 % queue) == head
- 队列空:head=tail
堆满的判断方式会浪费数组中一个元素。故循环队列可按照下列实现:
| queue_len = 100 |
队列的用途
队列一般用于缓存操作。比如消息队列,线程池等都是使用了队列。但是队列的大小设置是需要我们关注的。我个人主要的考虑依据是:在可接受的反应时间内,将队列设置到最大。
总结
本节主要介绍了栈数据结构,它具有先进后出,后进先出的操作特点。以及栈的在表达式和函数调用上的应用。一定要区别栈数据结构和内存中的栈不是完全相同的概念。算是交际关系.
队列的概念,并实现了队列和循环队列。以及队列大小设置的依据。
相关文章:

【追求卓越04】数据结构--栈与队列
引导 今天我们开始学习栈与队列的内容,我觉得栈并不难,所以篇幅也就不会那么多了。在虚拟空间中,栈是用户空间中的一种数据结构,它主要用于保存局部变量。那么问题来了,为什么用栈来保存局部变量,不用别的数…...

基于SpringBoot的超市信息管理系
✌全网粉丝20W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取项目下载方式🍅 一、项目背景介绍: 随着我国经济的不断发…...
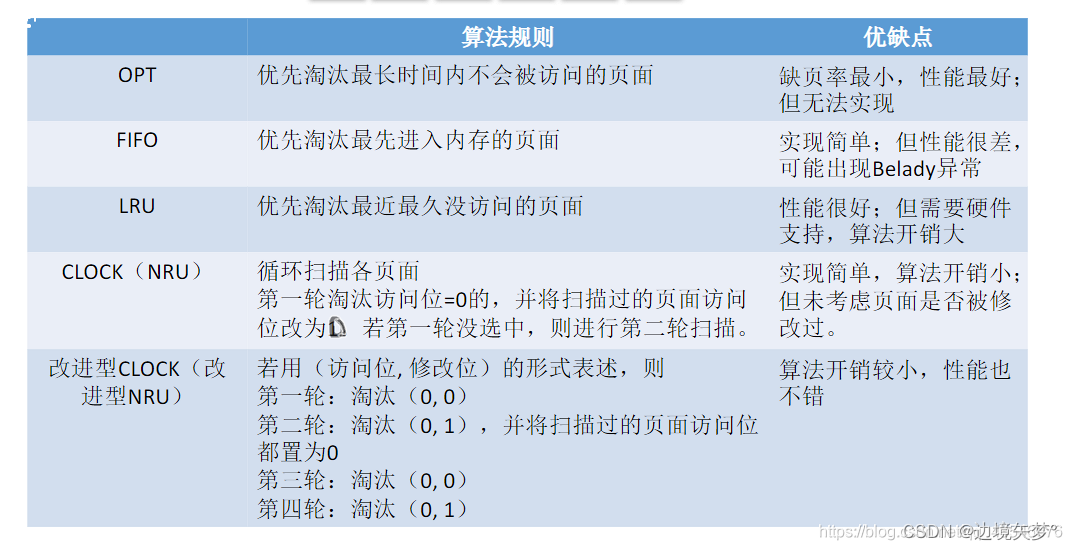
【计算机组成原理】存储系统
🎄欢迎来到边境矢梦的csdn博文🎄 🎄本文主要梳理计算机组成原理中 存储系统的知识点和值得注意的地方 🎄 🌈我是边境矢梦,一个正在为秋招和算法竞赛做准备的学生🌈 🎆喜欢的朋友可以…...
基于SSM的旅游管理系统设计与实现
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:采用JSP技术开发 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目&#x…...

JeecgBoot3.0 漏洞升级 — 快速文档
近几年来,黑客攻击行为呈现出日益复杂和隐蔽的趋势,对个人和组织的安全造成了严重威胁。黑客们不断寻找新的漏洞和安全漏洞,利用各种手段进行网络攻击,包括恶意软件、网络钓鱼、勒索软件等。因此,我们每个人都需要关注…...

6.一维数组——用冒泡法,选择法将5个整数由大到小排序
文章目录 前言一、题目描述 二、题目分析 三、解题 程序运行代码(冒泡法)程序运行代码(选择法) 前言 本系列为一维数组编程题,点滴成长,一起逆袭。 一、题目描述 用冒泡法将5个整数由大到小排序 二、题目…...

YOLOv8 onnx 文件推理多线程加速视频流
运行环境: MacOS:14.0Python 3.9Pytorch2.1onnx 运行时 模型文件: https://wwxd.lanzouu.com/iBqiA1g49pbc 密码:f40v 下载 best.apk后将后缀名修改为 onnx 即可模型在英伟达 T4GPU 使用 coco128 训练了 200 轮如遇下载不了可私信获取 代码…...
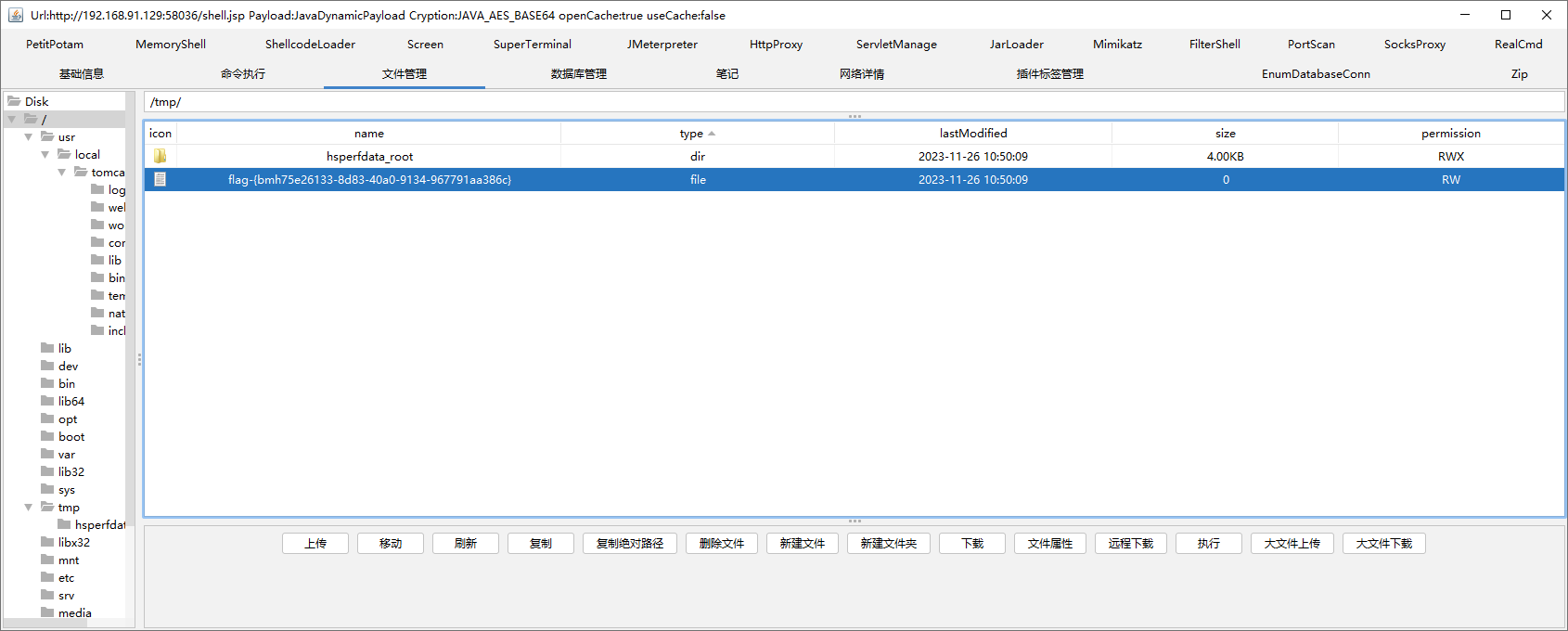
CVE-2017-12615 文件上传
CVE-2017-12615 文件上传 当存在漏洞的Tomcat运行在Windows/Linux主机上, 且启用了HTTP PUT请求方法( 例如, 将readonly初始化参数由默认值设置为false) , 攻击者将有可能可通过精心构造的攻击请求数据包向服务器上传…...
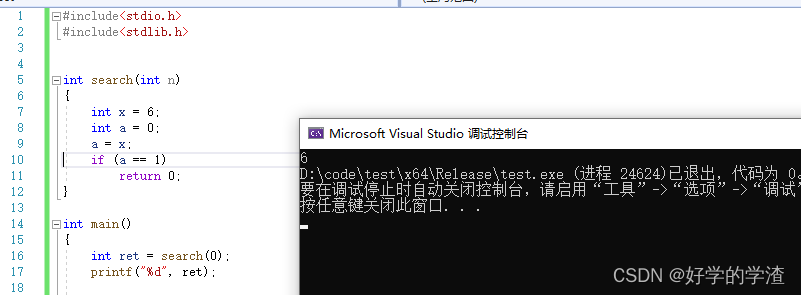
c++没有返回值的返回值
上面的函数search没有返回值,因为a不等于1,但是输出的时候会输出6.这恰巧是x的值,如果我们希望a不等于1时返回x,那么这种结果反而是正确的.有时候这种错误的代码可能产生正确的结果反而会加大debug难度 int search(int n) { 00007FF66DB723E0 mov dword ptr [rsp8],e…...

全网最全卡方检验汇总
一文整理了卡方检验全部内容,包括卡方检验的定义(基本思想、卡方值计算、适用条件分析)、卡方检验分类(2*2四格表卡方、R*C表格卡方、配对卡方、卡方拟合优度检验、分层卡方)、卡方检验如何分析(数据格式、…...
)
Java基础-中级-高级面试题汇(一)
第一部分: Java基础面试题汇总 1.面向对象和面向过程的区别? 面向对象和面向过程是两种不同的编程思想。面向对象是一种以对象为中心的编程思想,将数据和处理数据的方法封装在一起,形成一个类。程序通过创建对象来调用类中的方法…...

数据结构 / day04 作业
1. 单链表任意位置删除, 单链表任意位置修改, 单链表任意位置查找, 单链表任意元素查找, 单链表任意元素修改, 单链表任意元素删除, 单链表逆置 // main.c#include "head.h"int main(int argc, const char *argv[]) {Linklist headNULL; //head 是头指针// printf(&q…...
Java核心知识点整理大全20-笔记
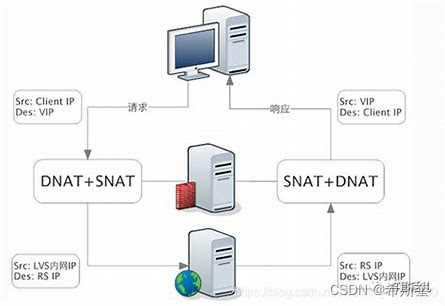
目录 17. 设计模式 17.1.1. 设计原则 17.1.24. 解释器模式 18. 负载均衡 18.1.1.1. 四层负载均衡(目标地址和端口交换) 18.1.1.2. 七层负载均衡(内容交换) 18.1.2. 负载均衡算法/策略 18.1.2.1. 轮循均衡(Roun…...

Spark---转换算子、行动算子、持久化算子
一、转换算子和行动算子 1、Transformations转换算子 1)、概念 Transformations类算子是一类算子(函数)叫做转换算子,如map、flatMap、reduceByKey等。Transformations算子是延迟执行,也叫懒加载执行。 2)、Transf…...

什么是关系型数据库?
什么是关系型数据库? 关系型数据库(RDBMS)是建立在关系模型基础上的数据库系统。关系模型是一种数据模型,它表示数据之间的联系,包括一对一、一对多和多对多的关系。在关系型数据库中,数据以表格的形式存储…...
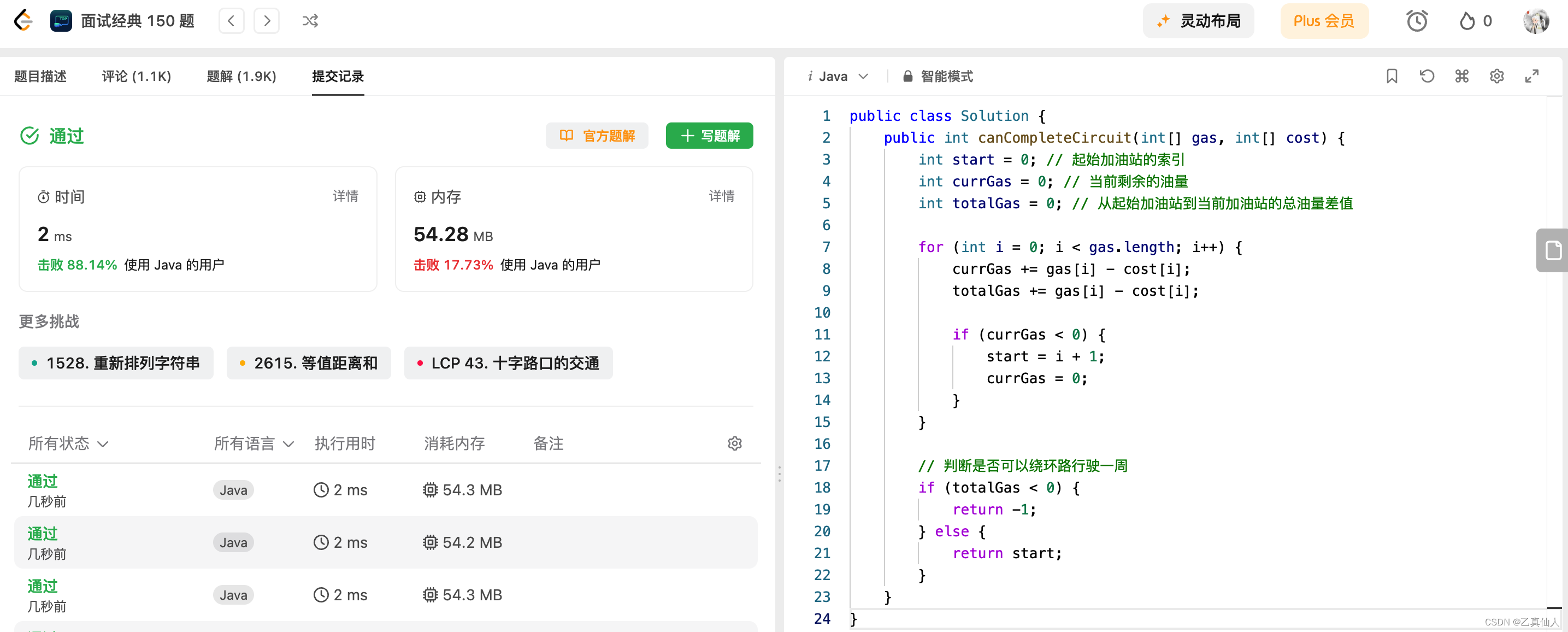
【LeetCode】挑战100天 Day12(热题+面试经典150题)
【LeetCode】挑战100天 Day12(热题面试经典150题) 一、LeetCode介绍二、LeetCode 热题 HOT 100-142.1 题目2.2 题解 三、面试经典 150 题-143.1 题目3.2 题解 一、LeetCode介绍 LeetCode是一个在线编程网站,提供各种算法和数据结构的题目&…...
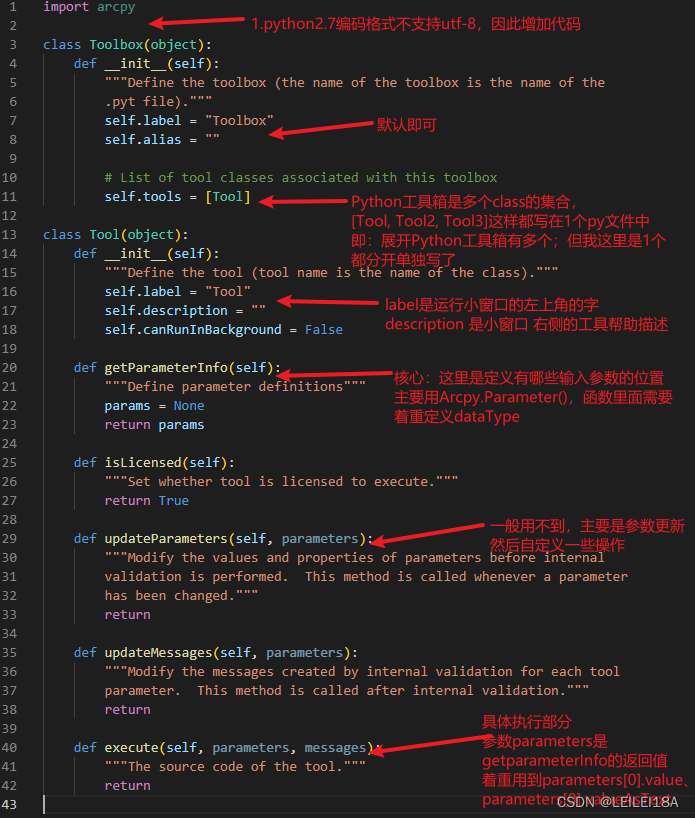
ArcGIS10.x系列 Python工具箱教程
ArcGIS10.x系列 Python工具箱教程 目录 1.前提 2.需要了解的资料 3.Python工具箱制作教程 4. Python工具箱具体样例代码(DEM流域分析-河网等级矢量化) 1.前提 如果你想自己写Python工具箱,那么假定你已经会ArcPy,如果只是自己…...
【蓝桥杯】刷题
刷题网站 记录总结刷题过程中遇到的一些问题 1、最大公约数与最小公倍数 a,bmap(int,input().split())sa*bwhile a%b:a,bb,a%bprint(b,s//b)2.迭代法求平方根(题号1021) #include<stdio.h> #include<math.h> int main() {double x11.0,x2;int a;scanf("%d&…...

软件产品登记的材料条件
(1)申请双软认证前应该要获得信息产业部授权的软件检测机构出具的检测证明,这份检测证明可以到软件行业协会申请,然后协会会派专家到公司进行“检测”,检测通过后出具证明,这份证明的申请与软件著作权等无关࿰…...

春节后跟进客户开发信模板?外贸邮件模板?
适合新年的客户开发信模板?年后给客户的邮件怎么写? 在春节这一传统的中国节日结束后,跟进客户对于维持和发展业务至关重要。客户开发信模板是一种有效的工具。蜂邮将介绍一些春节后跟进客户开发信模板的关键技巧,以确保您的业务…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

华为OD机考-机房布局
import java.util.*;public class DemoTest5 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseSystem.out.println(solve(in.nextLine()));}}priv…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...
