蓝桥杯day01——根据给定数字划分数组
题目描述
给你一个下标从 0 开始的整数数组 nums 和一个整数 pivot 。请你将 nums 重新排列,使得以下条件均成立:
- 所有小于
pivot的元素都出现在所有大于pivot的元素 之前 。 - 所有等于
pivot的元素都出现在小于和大于pivot的元素 中间 。 - 小于
pivot的元素之间和大于pivot的元素之间的 相对顺序 不发生改变。- 更正式的,考虑每一对
pi,pj,pi是初始时位置i元素的新位置,pj是初始时位置j元素的新位置。对于小于pivot的元素,如果i < j且nums[i] < pivot和nums[j] < pivot都成立,那么pi < pj也成立。类似的,对于大于pivot的元素,如果i < j且nums[i] > pivot和nums[j] > pivot都成立,那么pi < pj。
- 更正式的,考虑每一对
请你返回重新排列 nums 数组后的结果数组。
示例 1:
输入:nums = [9,12,5,10,14,3,10], pivot = 10 输出:[9,5,3,10,10,12,14] 解释: 元素 9 ,5 和 3 小于 pivot ,所以它们在数组的最左边。 元素 12 和 14 大于 pivot ,所以它们在数组的最右边。 小于 pivot 的元素的相对位置和大于 pivot 的元素的相对位置分别为 [9, 5, 3] 和 [12, 14] ,它们在结果数组中的相对顺序需要保留。
示例 2:
输入:nums = [-3,4,3,2], pivot = 2 输出:[-3,2,4,3] 解释: 元素 -3 小于 pivot ,所以在数组的最左边。 元素 4 和 3 大于 pivot ,所以它们在数组的最右边。 小于 pivot 的元素的相对位置和大于 pivot 的元素的相对位置分别为 [-3] 和 [4, 3] ,它们在结果数组中的相对顺序需要保留。
提示:
1 <= nums.length <= 105-106 <= nums[i] <= 106pivot等于nums中的一个元素。
解析
目标是将给定的整数列表nums根据指定的pivot值进行划分,使得左边的元素都小于pivot,右边的元素都大于pivot,而中间的元素则与pivot相等。
以下是代码的详细解析:
-
定义三个空列表:
left、right和between。这三个列表将分别存储小于pivot的元素、大于pivot的元素和等于pivot的元素。 -
遍历输入的列表
nums中的每个元素。对于每个元素,根据其值与pivot的比较结果,将其添加到相应的列表中:- 如果元素的值小于
pivot,则将其添加到left列表中。 - 如果元素的值大于
pivot,则将其添加到right列表中。 - 如果元素的值等于
pivot,则将其添加到between列表中。
- 如果元素的值小于
-
最后,将这三个列表连接起来并返回结果。这个结果是一个新的列表,其中包含按照要求排序的元素。
python代码
class Solution:def pivotArray(self, nums: List[int], pivot: int) -> List[int]:left=[]right=[]between=[]for x in nums:if x<pivot:left.append(x)elif x>pivot:right.append(x)else:between.append(x)return left+between+right运行结果

相关文章:

蓝桥杯day01——根据给定数字划分数组
题目描述 给你一个下标从 0 开始的整数数组 nums 和一个整数 pivot 。请你将 nums 重新排列,使得以下条件均成立: 所有小于 pivot 的元素都出现在所有大于 pivot 的元素 之前 。所有等于 pivot 的元素都出现在小于和大于 pivot 的元素 中间 。小于 piv…...
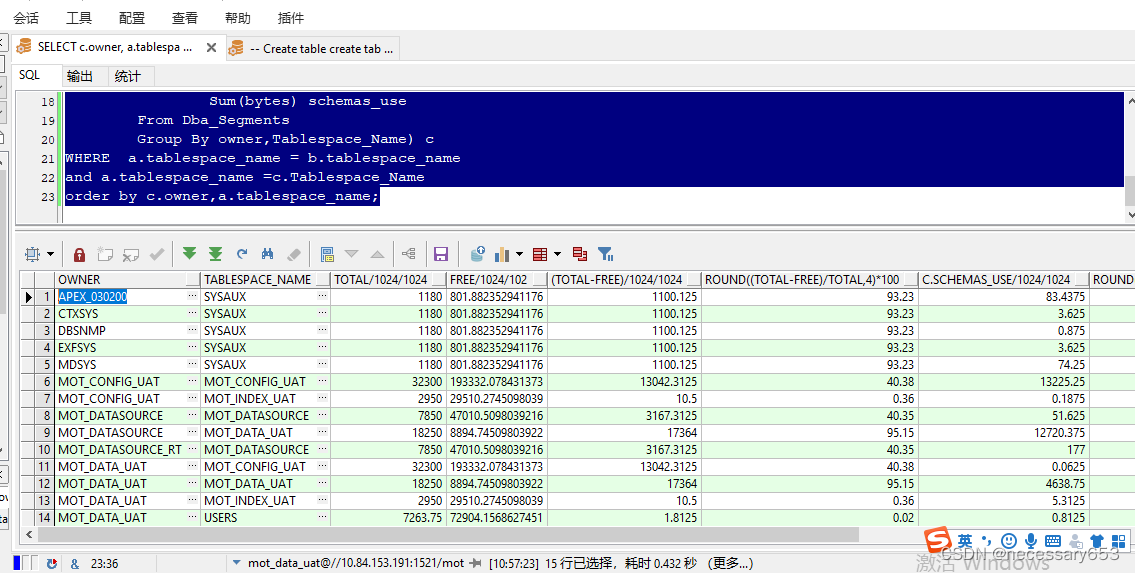
oracle数据库巡检常见脚本-系列二
简介 作为数据库管理员(DBA),定期进行数据库的日常巡检是非常重要的。以下是一些原因: 保证系统的稳定性:通过定期巡检,DBA可以发现并及时解决可能导致系统不稳定的问题,如性能瓶颈、资源利用率…...
JavaScript 表达式
JavaScript 表达式 目录 JavaScript 表达式 一、赋值表达式 二、算术表达式 三、布尔表达式 四、字符串表达式 表达式是一个语句的集合,计算结果是个单一值。 在JavaScript中,常见的表达式有4种: (1)赋值表达式…...
Python之Pygame游戏编程详解
一、介绍 1.1 定义 Pygame是一种流行的Python游戏开发库,它提供了许多功能,使开发人员可以轻松创建2D游戏。它具有良好的跨平台支持,可以在多个操作系统上运行,例如Windows,MacOS和Linux。在本文中,我们将…...
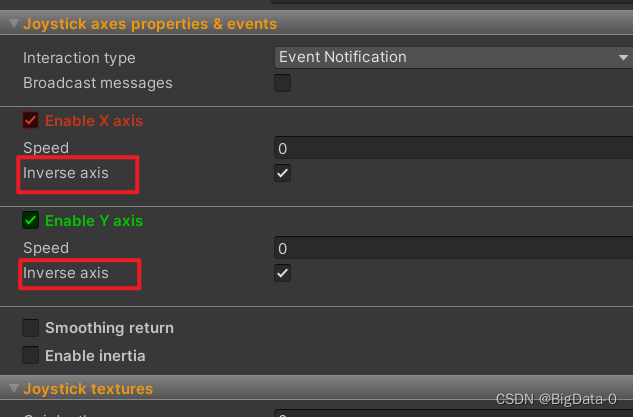
虚拟摇杆easytouch joystick的方向与角色移动方向不一致
更改 勾选 inverse axis 进行校正...

C++二分查找:统计点对的数目
本题其它解法 C双指针算法:统计点对的数目 本周推荐阅读 C二分算法:得到子序列的最少操作次数 本文涉及的基础知识点 二分查找算法合集 题目 给你一个无向图,无向图由整数 n ,表示图中节点的数目,和 edges 组成…...
:了解FFmpeg与SDL常用对象和函数)
播放器开发(二):了解FFmpeg与SDL常用对象和函数
学习课题:逐步构建开发播放器【QT5 FFmpeg6 SDL2】 前言 这一篇内容就是简单的了解一遍一些常用的函数名称和作用,混个眼熟。 能看源码的就去看源码!!! 能看源码的就去看源码!!! …...

【数据库】基于排序算法的去重,集合与包的并,差,交,连接操作实现原理,执行代价以及优化
基于两趟排序的其它操作 专栏内容: 手写数据库toadb 本专栏主要介绍如何从零开发,开发的步骤,以及开发过程中的涉及的原理,遇到的问题等,让大家能跟上并且可以一起开发,让每个需要的人成为参与者。 本专栏…...
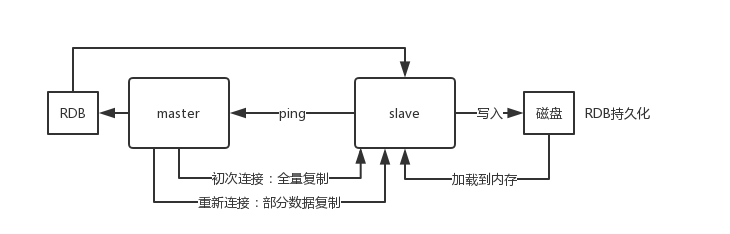
Redis 主从架构,Redis 分区,Redis哈希槽的概念,为什么要做Redis分区
文章目录 Redis 主从架构redis replication 的核心机制redis 主从复制的核心原理过程原理Redis集群的主从复制模型是怎样的?生产环境中的 redis 是怎么部署的?机器是什么配置?你往内存里写的是什么数据?说说Redis哈希槽的概念&…...

极客大挑战2023 Web方向题解wp 全
最后排名 9/2049。 玩脱了,以为28结束,囤的一些flag没交上去。我真该死啊QAQ EzHttp 前言:这次极客平台太安全了谷歌不给抓包,抓包用burp自带浏览器。 密码查看源码->robots.txt->o2takuXX’s_username_and_password.txt获…...
kafka开发环境搭建
文章目录 1 安装java环境1.1 下载linux下的安装包1.2 解压缩安装包1.3 解压后的文件移到/usr/lib目录下1.4 配置java环境变量 2 kafka的安装部署2.1 下载安装kafka2.2 配置和启动zookeeper2.3 启动和停止kafka 1 安装java环境 1.1 下载linux下的安装包 (1…...

Python大数据考题
Python大数据考题: 2022找工作是学历、能力和运气的超强结合体,遇到寒冬,大厂不招人,可能很多算法学生都得去找开发,测开 测开的话,你就得学数据库,sql,oracle,尤其sql要…...

才聚免费为你招聘,用人单位看过来!
才聚团队从1998年开始从事项目管理的推广工作,20多年来培训学员超30万人次,分布全国各地、服务企业超过5000家。拥有大批 PMP (项目管理专业人员资格) NPDP(产品经理国际资格) 软考 (信息系统…...
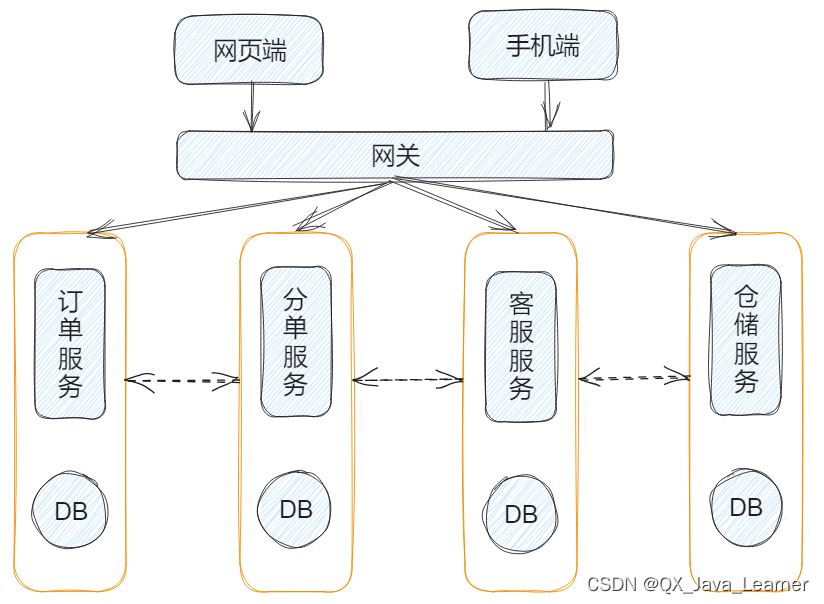
【SpringCloud】微服务的扩展性及其与 SOA 的区别
一、微服务的扩展性 由上一篇文章(没看过的可点击传送阅读)可知, 微服务具有极强的可扩展性,这些扩展性包含以下几个方面: 性能可扩展:性能无法完全实现线性扩展,但要尽量使用具有并发性和异步…...
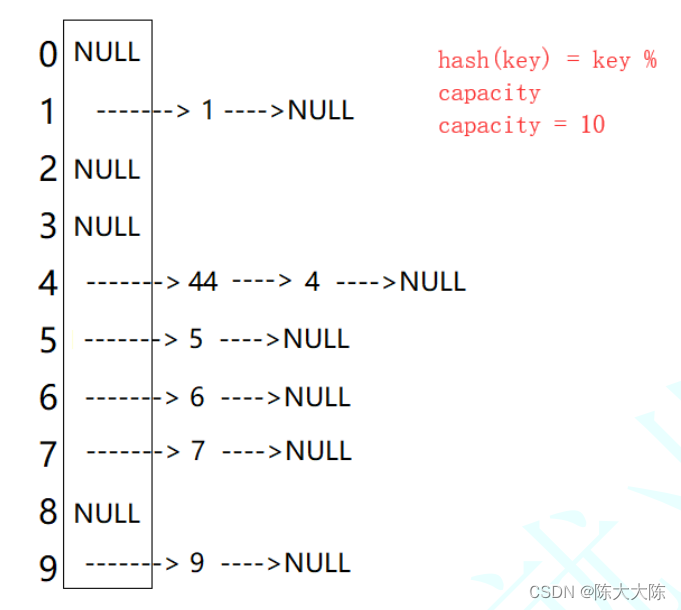
从零带你底层实现unordered_map (2)
💯 博客内容:从零带你实现unordered_map 😀 作 者:陈大大陈 🚀 个人简介:一个正在努力学技术的准C后端工程师,专注基础和实战分享 ,欢迎私信! 💖 欢迎大家…...

打造企业AI数字人专属IP的重要性
在数字化时代,企业数字人专属IP的打造成为了企业品牌建设的重要组成部分。企业数字人专属IP是指是利用人工智能技术实现与真人直播形象的1:1克隆,即克隆出一个数字化的真人形象,作为独有的企业数字人形象,可以用于产品推广、品牌宣…...
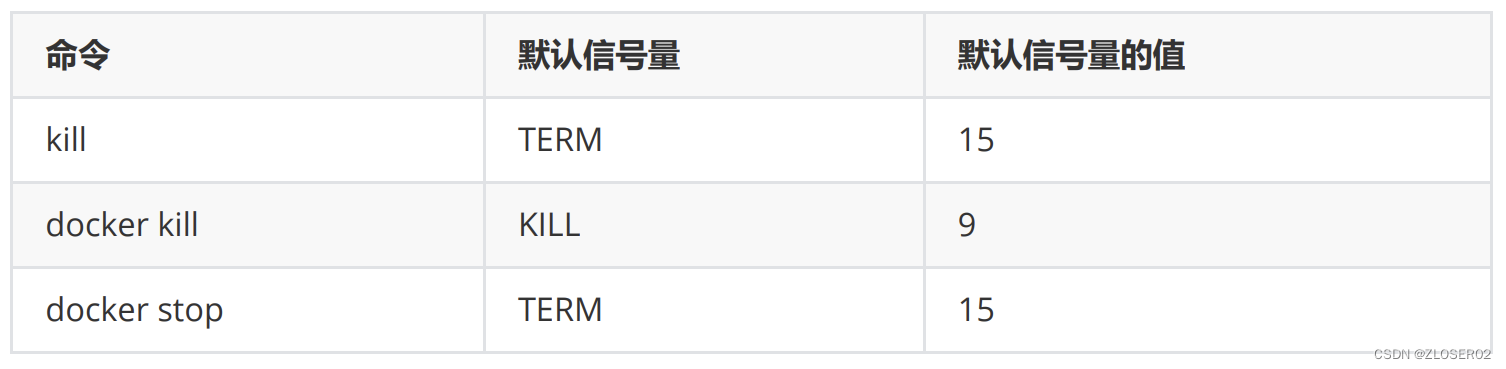
docker容器的生命周期管理常用命令
容器的生命周期管理命令 docker create :创建一个新的容器但不启动它 docker create nginx docker run :创建一个新的容器并运行一个命令 常用选项: 常用选项1. --add-host:容器中hosts文件添加 host:ip 映射记录 2. -a, --attach&#…...

CF 1900B Laura and Operations 学习笔记
原题链接 传送门 题意 输入三个数字a,b,c表示1,2,3的数目,也就是说有a个1,b个2,c个3,每一次可以删除两个不同的数字,增加一个剩下的数字,比如说删除1和3,增加2&#x…...

Linux学习笔记6-串口应用
到现在为止都是在开发板上运行的裸机程序,相当于之前学习STM32单片机时走过的路,还没有真正进入到核心的驱动开发部分,但这都是基础,所以慢慢来不着急。 接下来进入串口通信的学习,和GPIO一样,也是和单片机…...

ubuntu下如何查看.gz压缩包中的内容,以及grep过滤查找文件中的某些内容
1、查看压缩包file.gz中的全部内容 $ zcat file.gz 2、对一个.gz的压缩包解压缩 $ gunzip file.gz 3、过滤查找文件中的某些内容 $ grep "Hello" file.txt 注:我通常先解压,然后再grep 4、过滤查找文件中的内容,并显示其上下3行…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...
