PTA:用函数实现从数列中删除一个数
题目:
编写一个函数实现:删除n个元素的数列中下标为k的元素。
测试程序将输入一个下标值,调用本函数,删除数列{1,4,13,9,6,11,18,14,25}中该下标位置的元素,并输出删除后的数列。
函数接口定义:
void deleted ( int a[], int n, int k);
其中 a 、n和 k 都是用户传入的参数。 a是数列所在数组的首地址; n 是数列元素个数, k 是[0, 8]区间内的个位数。
裁判测试程序样例:
#include <stdio.h>
void deleted ( int a[], int n, int k);
int main()
{int a[9]={1,4,13,9,6,11,18,14,25},k;int i;scanf("%d",&k);deleted(a,9,k);for(i=0;i<8;i++)printf("%4d", a[i]);return 0;}
/*请将答案写在这里*/
输入样例:
输入一个[0,8]间的个位数
0
输出样例:
输出数组中各元素占4列
4 13 9 6 11 18 14 25
解题过程
#include <stdio.h>
void deleted(int a[], int n, int k){if (k < 0 || k >= n){return;}for (int i = k; i < n - 1; i++) {a[i] = a[i + 1]; }
}
相关文章:

PTA:用函数实现从数列中删除一个数
题目: 编写一个函数实现:删除n个元素的数列中下标为k的元素。 测试程序将输入一个下标值,调用本函数,删除数列{1,4,13,9,6,11,18,14,25}中该下标位置的元素,并输出删除后的数列。 函数接口定义: void de…...
C++设计模式之工厂模式(中)——工厂模式
工厂模式 工厂模式介绍示例示例使用运行结果工厂模式与简单工厂模式区别 工厂模式 工厂模式在简单工厂模式的基础之上进行了改进。当需要生产的产品种类增加,可以通过新增子类工厂来生产,没有破坏程序设计原则中的开放封闭原则。 介绍 工厂模式先抽象…...

关于el-table的二次封装及使用,支持自定义列内容
关于el-table的二次封装及使用 table组件 <template><el-table ref"tableComRef" :data"tableData" border style"width: 100%"><el-table-column v-if"tableHeaderList[0]?.type selection" type"selection&…...

【Vue】Vue3 配置全局 scss 变量
variables.scss $color: #0c8ce9;vite.config.ts // 全局css变量css: {preprocessorOptions: {scss: {additionalData: import "/styles/variables.scss";,},},},.vue 文件使用...
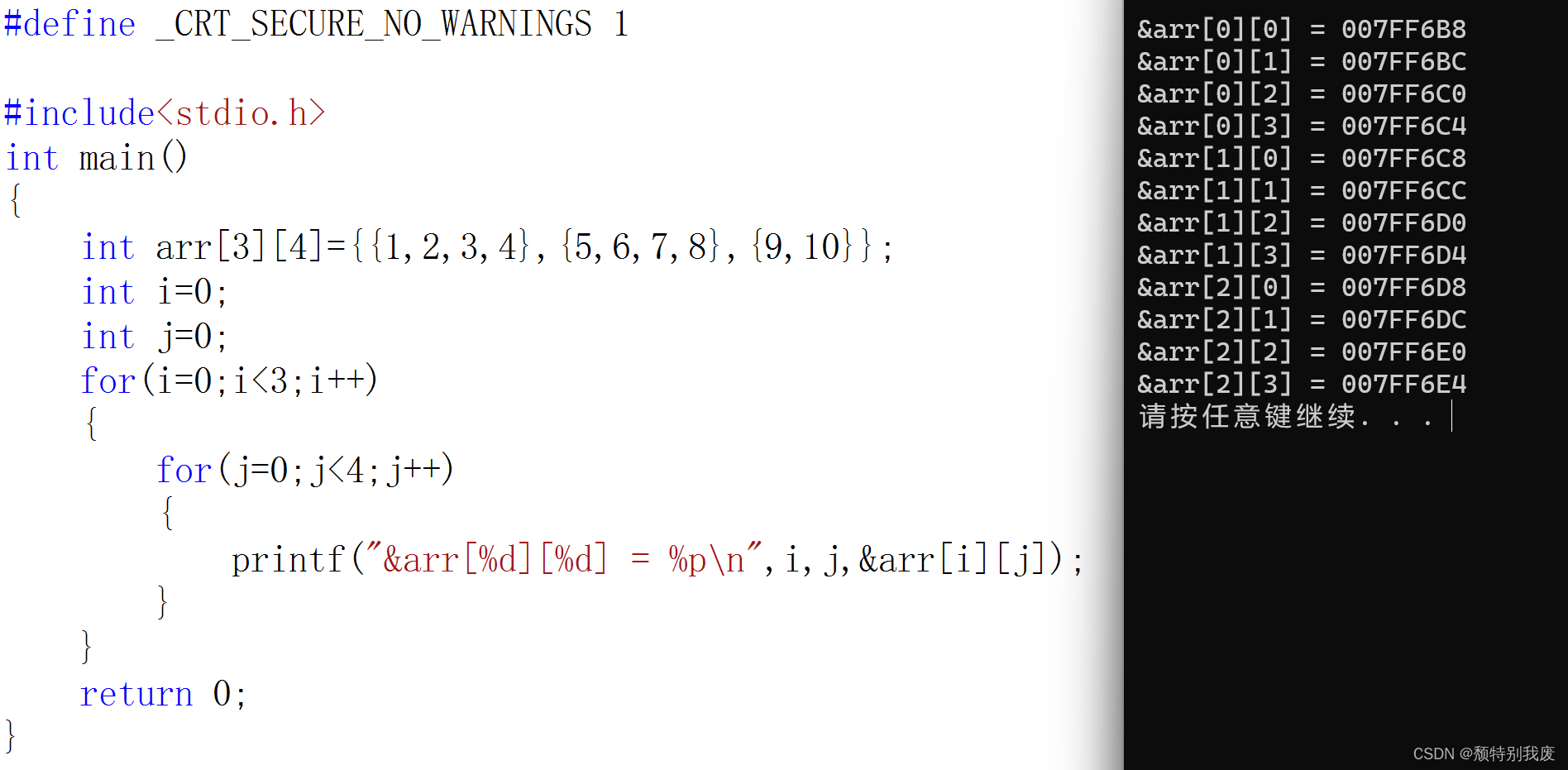
C语言—二维数组
一、二维数组的创建 int arr[3][4];char arr[3][5];double arr[2][4]; 数组创建:“[ ]”中要给一个常量,不能使用变量 二、二维数组的初始化 int arr[3][4]{1,2,3,4};int arr[3][4]{{1,2},{4,5}};int arr[][4]{{2,3},{4,5}}; 前面的为行,…...
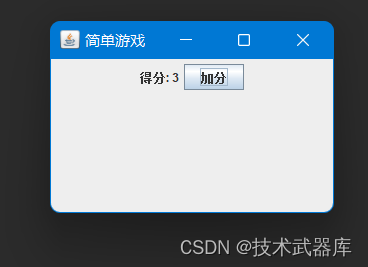
GUI加分游戏
需求目标 这个简单的游戏窗口包含一个得分标签和一个按钮。每次点击按钮时,得分增加1,并更新得分标签的显示。 效果 源码 /*** author lwh* date 2023/11/28* description 这个简单的游戏窗口包含一个得分标签和一个按钮。每次点击按钮时,…...

多线程的重要资料-信号量
(1)https://www.cnblogs.com/ike_li/p/8984186.html (2)C#关于AutoResetEvent的使用介绍 | 康瑞部落 (3)AutoResetEvent用法(一)_autoresetevent 的用法-CSDN博客 (4)c++ - Is there an easy way to implement AutoResetEvent in C++0x? - Stack Overflow (5)...

区块链相关技术、概念以及技术实现过程中的一些关键问题 Smart Contracts and Blockchains
作者:禅与计算机程序设计艺术 1.简介 2017年底,区块链已经成为众多投资人和技术人员最关注的话题之一。随着现实世界的不断复杂化、数字货币的流行以及IoT设备的普及,加密数字货币市场正变得越来越活跃。由于区块链具有去中心化、不可篡改、透明性、高并发等特点,使其在金…...

黑马点评Redis笔记
黑马点评Redis笔记 Redis基础篇:https://cyborg2077.github.io/2022/10/21/RedisBasic/ Redis实战篇:https://cyborg2077.github.io/2022/10/22/RedisPractice/ 一、手机号验证码注册登录 RandomUtil 生成定长随机数列 String code RandomUtil.ran…...
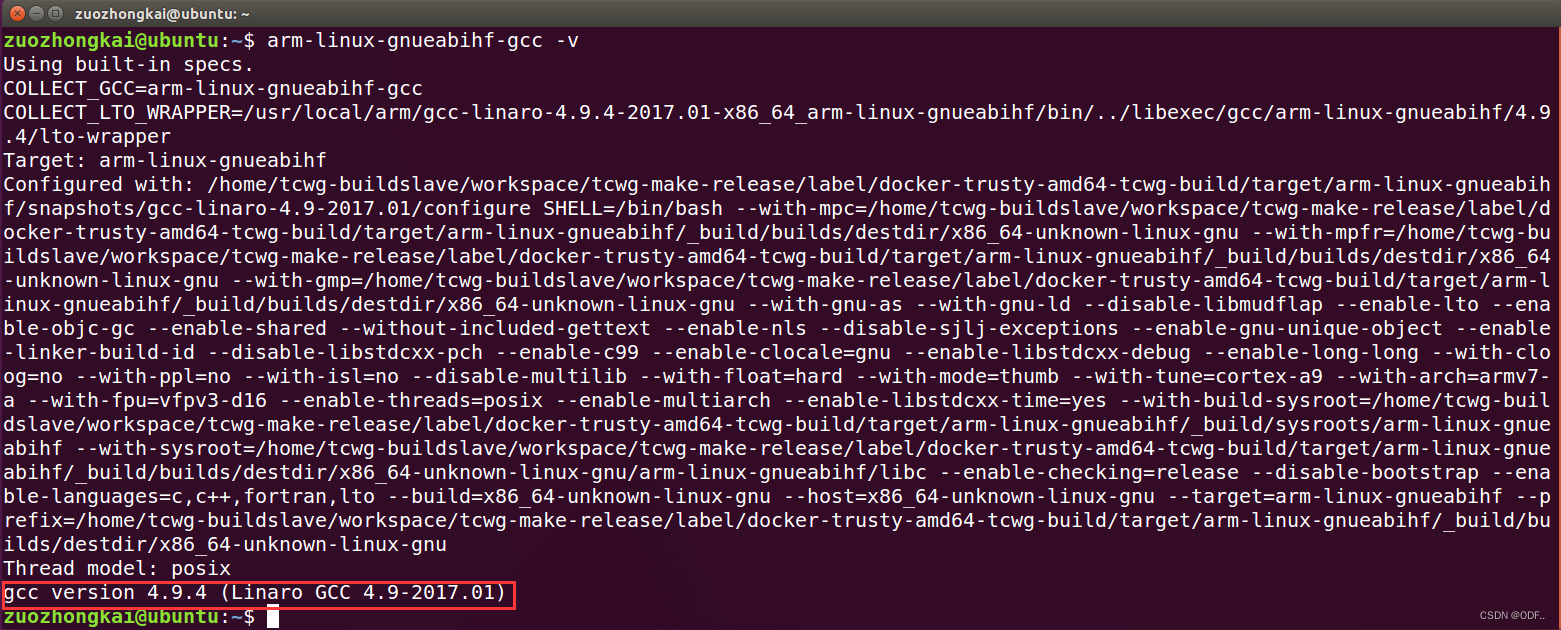
MX6ULL学习笔记 (一)交叉工具链的安装
前言: ARM 裸机、Uboot 移植、Linux 移植这些都需要在 Ubuntu 下进行编译,编译就需要编译 器,Ubuntu 自带的 gcc 编译器是针对 X86 架构的!而我们现在要编译的是 ARM 架构的代码,因为我们编译的代码是需要烧写到ARM板子…...

uni-app中的onLoad不执行
问题 想在onLoad()中发请求获取数据,却发现onLoad()根本不会执行 原因 这个页面没有在pages.json中配置,不属于uni-app中的页面 uni-app的文档也做出了说明,组件是无法使用页面级的onLoad等生命周期的 解决方法 uni-app除支持页面生命周…...
EFAK-v3.0.1版部署与使用
一、前言 EFAK((Eagle For Apache Kafka,以前称为Kafka Eagle)用于在使用 Topic 的情况下监控 Kafka 集群。包含Offset 的产生、Lag的变化、Partition的分布、Owner、Topic的创建以及修改的时间等信息。 二、环境&安装包 官方下载连接E…...

股票技术从初级到高级,从实盘进阶到摩尔缠论
一、教程描述 摩尔缠论是什么?一个伟大的缠论分支体系,由顶尖高手创立的缠论分支,这个顶尖高手,江湖上的代号为摩尔,可能是一个人,或者是一群人。摩尔缠论,基于缠论的核心思想与基础理论&#…...

力扣105. 从前序与中序遍历序列构造二叉树
栈 思路: 先序遍历:根、左子树、右子树;中序遍历:左子树、根、右子树;遍历先序遍历数组 prev,使用一个辅助栈缓存“根节点”;通过栈顶“根节点”与中序遍历数组 in 比较,确认是否到…...
Windows环境下的JDK安装与环境配置
一、JDK下载 1、打开Oracle官方网站下载页 Java Downloads | Oracle 中国 2、选择Java archive页,在版本列表中选择需要下载的版本 3、选择系统环境对应的版本,点击对应的下载按钮,弹出技术许可勾选框 4、勾选Oracle技术许可协议 5、输入Or…...
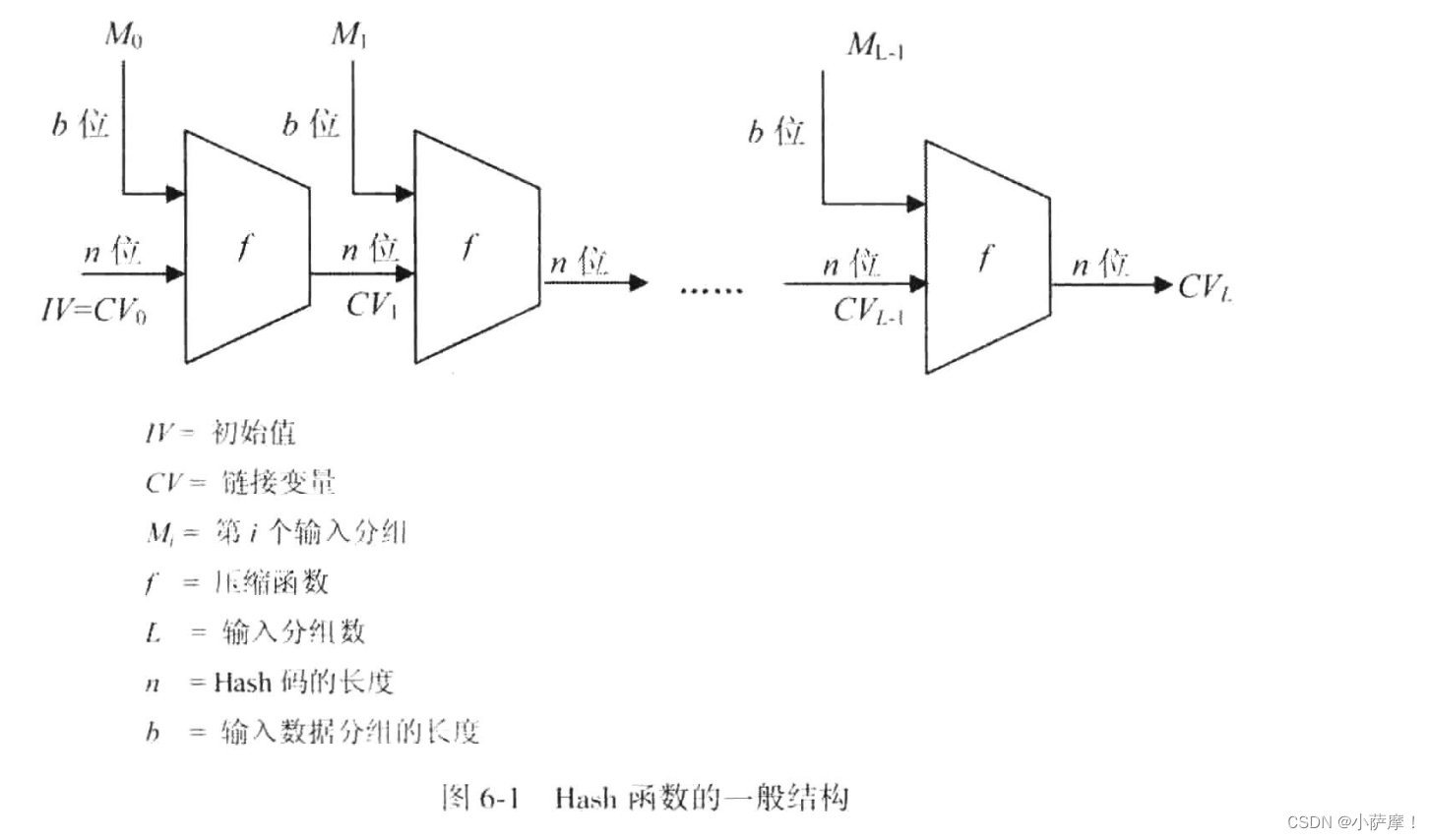
【密码学引论】Hash密码
第六章 Hash密码 md4、md5、sha系列、SM3 定义:将任意长度的消息映射成固定长度消息的函数功能:确保数据的真实性和完整性,主要用于认证和数字签名Hash函数的安全性:单向性、抗若碰撞性、抗强碰撞性生日攻击:对于生日…...

【传智杯】儒略历、评委打分、萝卜数据库题解
🍎 博客主页:🌙披星戴月的贾维斯 🍎 欢迎关注:👍点赞🍃收藏🔥留言 🍇系列专栏:🌙 蓝桥杯 🌙请不要相信胜利就像山坡上的蒲公英一样唾手…...
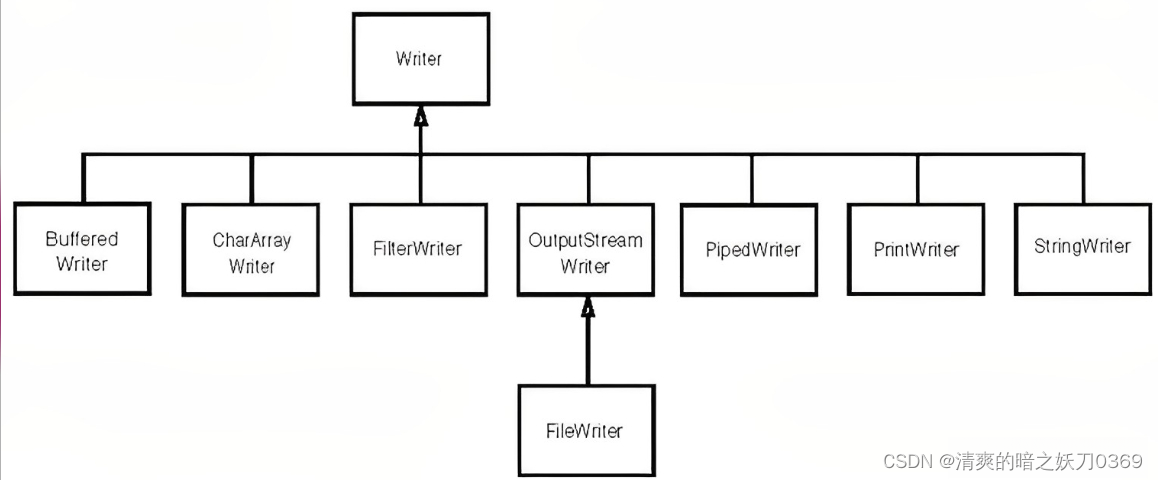
java基础-IO
1、基础概念 1.1、文件(File) 文件的读写可以说是开发中必不可少的部分,因为系统会存在大量处理设备上的数据,这里的设备指硬盘,内存,键盘录入,网络传输等。当然这里需要考虑的问题不仅仅是实现,还包括同步…...
Java变量理解
成员变量VS局部变量的区别 语法形式:从语法形式上看,成员变量是属于类的,而局部变量是在代码块或方法中定义的变量或是方法的参数;成员变量可以被 public,private,static 等修饰符所修饰,而局部变量不能被访问控制修饰…...
)
西南科技大学信号与系统A实验二(信号频谱分析)
一、实验目的 1.掌握用 matlab 软件绘制信号频谱的方法; 2.进一步理解抽样定理; 3.理解傅里叶变换的性质(频移特性). 二、实验原理 (一)fft 函数的调用 matlab 提供 fft 函数来计算信号 x(n)的快速离散傅里叶变换 (FFT). z 格式:y=fft(x) 计算信号 x 的快速离散傅里叶…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

文件上传漏洞防御全攻略
要全面防范文件上传漏洞,需构建多层防御体系,结合技术验证、存储隔离与权限控制: 🔒 一、基础防护层 前端校验(仅辅助) 通过JavaScript限制文件后缀名(白名单)和大小,提…...

GAN模式奔溃的探讨论文综述(一)
简介 简介:今天带来一篇关于GAN的,对于模式奔溃的一个探讨的一个问题,帮助大家更好的解决训练中遇到的一个难题。 论文题目:An in-depth review and analysis of mode collapse in GAN 期刊:Machine Learning 链接:...
