股票技术从初级到高级,从实盘进阶到摩尔缠论

一、教程描述
摩尔缠论是什么?一个伟大的缠论分支体系,由顶尖高手创立的缠论分支,这个顶尖高手,江湖上的代号为摩尔,可能是一个人,或者是一群人。摩尔缠论,基于缠论的核心思想与基础理论,走出了一条自己的路子,相比于缠师的原始缠论,更加适合普通投资者学习。本套股票教程,大小21.56G,共有70个文件。
二、教程目录
(一)、初级课程(实盘讲解)
01-炒股软件使用.mp4
02-认识K线图的形态(1).mp4
03-认识K线图的形态(2).mp4
04-什么是股票的盘口.mp4
05-怎么看分时图.mp4
06-如何买卖股票.mp4
07-成交量与换手率的看法.mp4
08-MACD的背离怎么看.mp4
09-KDJ指标详细解说.mp4
10-什么是行业板块与概念板块.mp4
11-画线工具使用方法.mp4
12-什么是大盘指数.mp4
13-涨停板与跌停板介绍.mp4
14-什么是缺口.mp4
15-怎么看区分小-中-大盘股.mp4
16-股票F10资料介绍.mp4
17-什么是建仓-洗盘-出货.mp4
18-什么是组合K线.mp4
19-怎么看筹码分布图指标.mp4
20-选股工具讲解.mp4
21-什么是移动均线.mp4
22-移动均线怎么看.mp4
23-上升与下跌通道线的画法.mp4
24-上涨趋势与下跌趋势线的正确画法.mp4
25-经典技术指标-黄金分割线的画法与用法.mp4
(二)、中级课程(股票进阶)
01-中级-筹码分布图的单封密集与双峰填谷.mp4
02-中级-如何用筹码指标找支撑位与压力位.mp4
03-中级-筹码分布图的选股技巧.mp4
04-中级-从筹码分布图看出货与洗盘.mp4
05-中级-股票的支撑位与压力位.mp4
06-中级-股票止损方法与技巧.mp4
07-中级-怎么看股票的基本面.mp4
08-中级-什么样的股票具备高送转的潜力.mp4
09-中级-最佳选股技巧-.mp4
10-中级-换手率的正确看法.mp4
11-中级-行情直播课程【15分钟后重点】.mp4
(三)、高级课程(摩尔缠论1)
基础01 笔、线段、线段的画法.mp4
基础02 线段中枢的唯一.mp4
基础03 线段转折、延伸(上).mp4
基础04 线段延伸之向下延伸.mp4
基础05 延段延伸的融合贯通.mp4
基础06 线段顶底的唯一.mp4
基础07 走势分类之本级别中枢.mp4
基础08 走势分类之走势的理解.mp4
基础09 走势之级别.mp4
基础10 走势终完美.mp4
基础11 同级别分解.mp4
基础12 走势分类唯一之同级别分解.mp4
基础13 走势分类的唯一.mp4
基础14 第一类买点.mp4
基础15 第一类卖点.mp4
基础16 第二类买点.mp4
基础17 第二类卖点和第三类买点.mp4
基础18 第三类卖点.mp4
基础19 买卖点量化.mp4
基础20 选股.mp4
基础21 交易成长.mp4
(四)、高级课程(摩尔缠论2)
01开班课程.mp4
02第一讲:线段的静动理解及运用.mp4
03第二讲:线段的动态之延伸.mp4
04第三讲:线段的全新延伸.mp4
05第四讲:职业交易必备:操作系统下的线段处理.mp4
06第五讲:职业交易必备:选股角度下的线段.mp4
07第六讲:职业交易者的走势终完美.mp4
08第七讲:职业交易者走势终完美之选股运用再理解.mp4
09第八讲:职业交易者的择时.mp4
10第九讲:职业交易者的走势理解.mp4
11第十讲:职业交易者的买卖点理解.mp4
12第十一讲:职业交易者的股市理解.mp4
13第十二讲:职业交易者的必备.mp4
三、教程下载
百度一下“宝贝分享网”,站内搜索关键词获取。
相关文章:

股票技术从初级到高级,从实盘进阶到摩尔缠论
一、教程描述 摩尔缠论是什么?一个伟大的缠论分支体系,由顶尖高手创立的缠论分支,这个顶尖高手,江湖上的代号为摩尔,可能是一个人,或者是一群人。摩尔缠论,基于缠论的核心思想与基础理论&#…...

力扣105. 从前序与中序遍历序列构造二叉树
栈 思路: 先序遍历:根、左子树、右子树;中序遍历:左子树、根、右子树;遍历先序遍历数组 prev,使用一个辅助栈缓存“根节点”;通过栈顶“根节点”与中序遍历数组 in 比较,确认是否到…...
Windows环境下的JDK安装与环境配置
一、JDK下载 1、打开Oracle官方网站下载页 Java Downloads | Oracle 中国 2、选择Java archive页,在版本列表中选择需要下载的版本 3、选择系统环境对应的版本,点击对应的下载按钮,弹出技术许可勾选框 4、勾选Oracle技术许可协议 5、输入Or…...
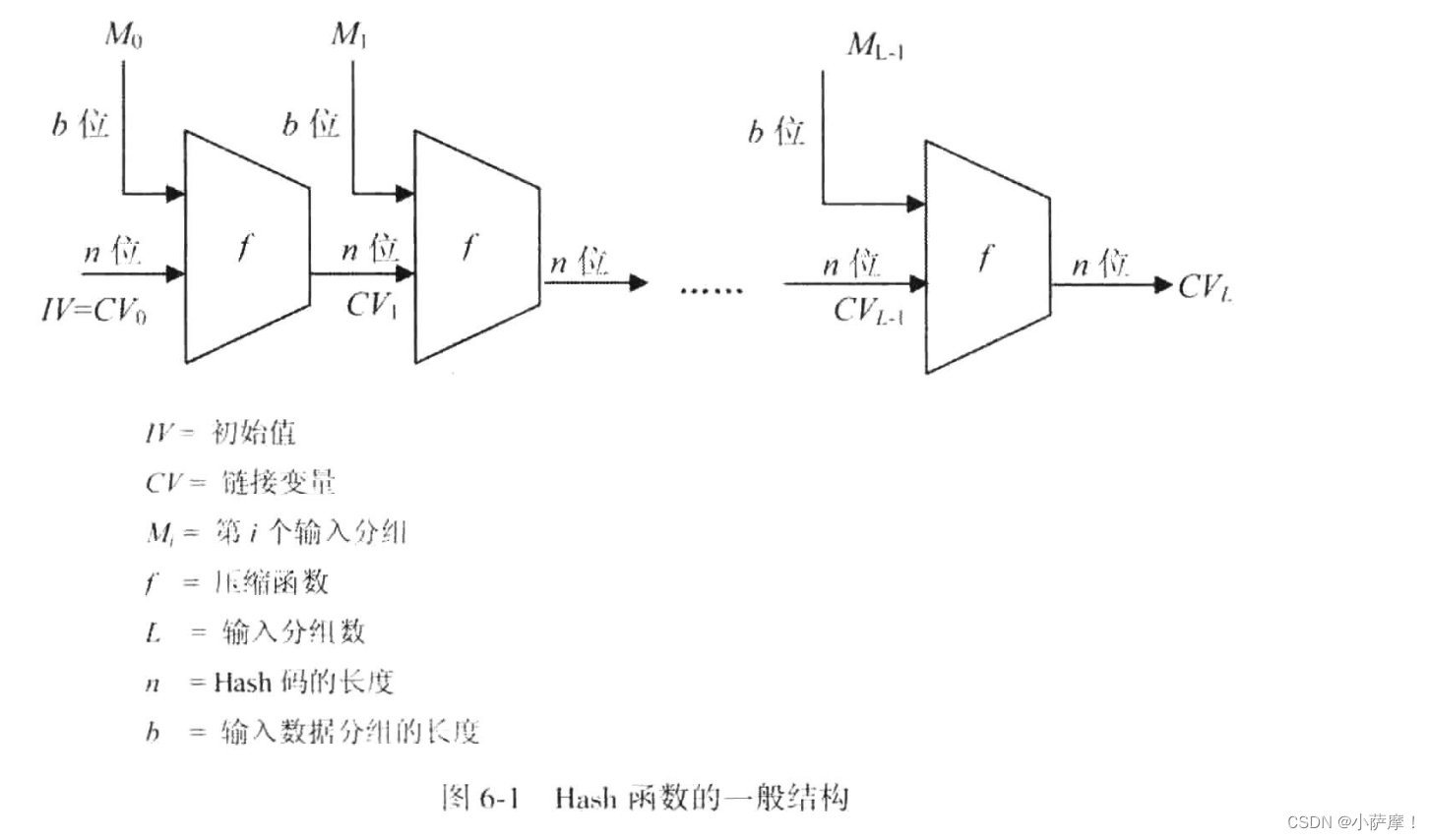
【密码学引论】Hash密码
第六章 Hash密码 md4、md5、sha系列、SM3 定义:将任意长度的消息映射成固定长度消息的函数功能:确保数据的真实性和完整性,主要用于认证和数字签名Hash函数的安全性:单向性、抗若碰撞性、抗强碰撞性生日攻击:对于生日…...

【传智杯】儒略历、评委打分、萝卜数据库题解
🍎 博客主页:🌙披星戴月的贾维斯 🍎 欢迎关注:👍点赞🍃收藏🔥留言 🍇系列专栏:🌙 蓝桥杯 🌙请不要相信胜利就像山坡上的蒲公英一样唾手…...
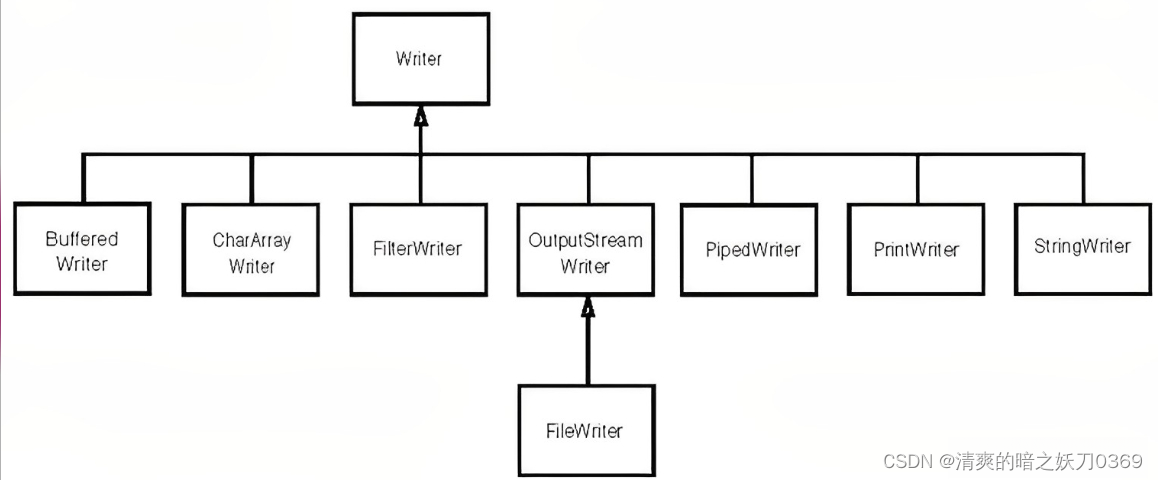
java基础-IO
1、基础概念 1.1、文件(File) 文件的读写可以说是开发中必不可少的部分,因为系统会存在大量处理设备上的数据,这里的设备指硬盘,内存,键盘录入,网络传输等。当然这里需要考虑的问题不仅仅是实现,还包括同步…...
Java变量理解
成员变量VS局部变量的区别 语法形式:从语法形式上看,成员变量是属于类的,而局部变量是在代码块或方法中定义的变量或是方法的参数;成员变量可以被 public,private,static 等修饰符所修饰,而局部变量不能被访问控制修饰…...
)
西南科技大学信号与系统A实验二(信号频谱分析)
一、实验目的 1.掌握用 matlab 软件绘制信号频谱的方法; 2.进一步理解抽样定理; 3.理解傅里叶变换的性质(频移特性). 二、实验原理 (一)fft 函数的调用 matlab 提供 fft 函数来计算信号 x(n)的快速离散傅里叶变换 (FFT). z 格式:y=fft(x) 计算信号 x 的快速离散傅里叶…...

C++-youtube cherno C++视频的一些知识点
对函数的调用在汇编中对应一句call func语句,其中func是一个函数的签名(signature)对程序而言,即使只有一个文件,链接器也需要链接,因为它需要链接程序入口点(entry point)一个程序的…...

sed命令
目录 一、sed 1.sed命令选项 2.语法选项 3.sed脚本格式 4.搜索替代 5.分组后向引用 1.提取版本号: 2.提取IP地址 3.提取数字权限 6.变量 二、免交互 1.多行重定向 2.免交互脚本 总结:本章主要介绍了seq和免交互的用法及相关知识 一、sed s…...

【经验分享】开发问题记录总结(持续更新)
目录 工具开发 界面类继承某自定义界面类时,出现布局混乱或者所有控件集中在左上角? 在继承自定义界面之后,以诸如 on_xxx_clicked() 模式设计的槽函数失效了? 使用pugi接口取出文本数据后,为什么该变量无法进行字符串比较&…...

MySQL导出数据库中每个表前 3000 条数据
以下是一个 Bash 脚本,它会连接到 MySQL 数据库,获取所有表名,并对每个表导出前 3000 条数据: #!/bin/bashUSERNAME"citycard" PASSWORD"密码" DATABASE"citycard" LIMIT3000# 导出数据库结构 mys…...

Spring事件注解@EventListener【观察】
一、背景 在开发工作中,我们常常会遇到这样一种情况:完成一项任务后,需要向其他模块广播消息或通知,以触发其他事件的处理。逐个发送请求固然可行,但更好的方式是采用事件监听,它是设计模式中的发布-订阅模…...

玩转Spring中强大的spel表达式!
玩转Spring中强大的spel表达式!值得推荐的好文:https://zhuanlan.zhihu.com/p/174786047...

HTTPS攻击原理 被攻击该如何防护
简单来说,HTTPS HTTP SSL/TLS。 在 HTTP 协议中,客户端通过网络传输消息与服务器进行通信。但该消息采用明文的原始格式。坏人(攻击者)很容易窃听消息。这就是我们需要 SSL/TLS 的原因。 HTTPS是一种安全的HTTP协议,…...
应用详解)
【.NET Core】委托(Delegate)应用详解
【.NET Core】委托(Delegate)应用详解 文章目录 【.NET Core】委托(Delegate)应用详解一、概述二、委托(Delegate)定义三、基础委托(Delegate) - 无返回值委托四、基础委托(Delegate) - 有返回值委托五、Mu…...

【LeetCode:1457. 二叉树中的伪回文路径 | 二叉树 + DFS +回文数】
🚀 算法题 🚀 🌲 算法刷题专栏 | 面试必备算法 | 面试高频算法 🍀 🌲 越难的东西,越要努力坚持,因为它具有很高的价值,算法就是这样✨ 🌲 作者简介:硕风和炜,…...

《golang设计模式》第三部分·行为型模式-06-备忘录模式(Memento)
文章目录 1. 概述1.1 角色1.2 类图 2. 代码示例2.1 设计2.2 代码2.3 类图 1. 概述 备忘录(Memento)用于在不破坏目标对象封装特性的基础上,将目标对象内部的状态存储到外部对象中,以备之后恢复状态时使用。 1.1 角色 Originato…...
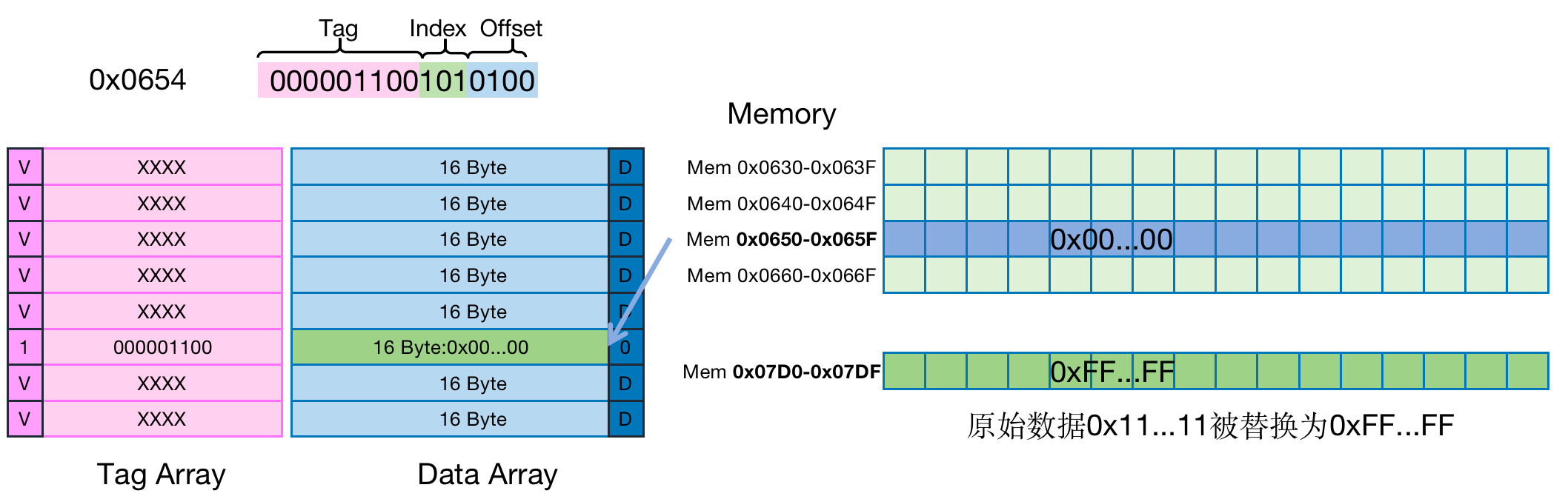
Cache学习(4):Cache分配策略Cache更新策略Cache逐出策略
Cache的数据流 常用名词 Allocation 分配Eviction 驱逐分配策略和更新策略分别为当产生Cache miss和Cache hit的时候数据流的具体行为 1 Cache分配策略(Cache Allocation Policy) Cache的分配策略是指不同情况下为数据分配Cache Line的不同行为。Cac…...

角色管理--产品经理岗
研发组织管理--角色管理--产品经理岗 定位 相对稳定和简单产品的独立产品打造者,复杂产品的辅助者 所需资质 校招新人,拥有灵性拥有基础的产品力(认知,设计,创新,推进,学习)Axur…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...
