科学与工程计算基础(数值计算)知识点总结
数值计算
- 第1章 概论
- 1.2 数值计算中的误差
- 1.2.1 误差的来源和分类
- 1.2.2 误差与有效数字
- 1.2.3 数值运算的误差估计
- 1.3 误差定性分析和避免误差危害
- 1.3.1 算法的数值稳定性
- 1.3.3 避免误差危害
- 1.4 数值计算中算法设计的技术
- 1.5 习题
- 1.5.1 判断题
- 1.5.2 计算题
- 第2章 插值法
- 2.2 拉格朗日插值
- 2.3 牛顿插值
- 2.4 埃尔米特插值
- 2.5 分段低次插值
- 2.6 三次样条插值
- 第3章 函数逼近与快速傅里叶变换
- 3.4 曲线拟合的最小二乘法
- 第4章 数值积分与数值微分
- 4.1 数值积分概论
- 4.2 牛顿-柯特斯公式
- 4.3 复合求积公式
- 4.4 龙贝格求积公式
- 4.5 自适应积分方法
- 4.6 高斯求积公式
- 第5章 解线性方程组的直接方法
- 5.2 高斯消去法
- 5.3 矩阵三角分解法
- 5.4 向量和矩阵范数
- 5.5 误差分析
- 第6章 解线性方程组的迭代法
- 6.2 雅可比迭代法与高斯-塞德尔迭代法
- 6.3 超松弛迭代法
- 第7章 非线性方程与方程组的数值解法
- 7.1 方程求根与二分法
- 7.2 不动点迭代法及其收敛性
- 7.3 迭代收敛的加速方法
- 7.4 牛顿法
- 第9章 常微分方程初值问题数值解法
- 9.2 简单的数值方法
第1章 概论
1.2 数值计算中的误差
1.2.1 误差的来源和分类
| 误差类型 | 介绍 | 示例 |
|---|---|---|
| 模型误差 | 在建立数学模型过程中,要将复杂的现象抽象归结为数学模型,往往要忽略一些次要因素的影响,而对问题作一些简化,因此和实际问题有一定的区别。 | 地球的体积使用球体体积公式 v = 4/3 Π R3 来近似计算 |
| 观测误差 | 在建模和具体运算过程中所用的数据往往是通过观察和测量得到的,由于精度的限制,计算这些数据一般是近似的 | 观测地球半径R的值 |
| 截断误差(方法误差) | 当数学模型不能得到精确解时,通常要用数值方法求它的近似解,其近似解与精确解之间的误差称为截断误差或方法误差 | 使用泰勒公式来计算可微函数某点值,其截断误差为泰勒余项 |
| 舍入误差 | 由于计算机字长有限,原始数据在计算机上表示时产生的误差 | Π 用 3.1415926 来近似、4/3 用 1.333333 来近似 |
1.2.2 误差与有效数字
| 误差 | 定义 | 示例 |
|---|---|---|
| 绝对误差(e*) | 设 x 为准确值,x* 为 x 的一个近似值,称 e* = x* - x 为近似值的绝对误差,简称误差 | 一般无法测量出精确值,所以绝对误差一般无法表示 |
| 绝对误差限(ε*) | 估计出绝对误差的一个上界 ε* ,即:| e* | = | x* - x | ≤ ε* | 测量某物品的长度为 20 ± 0.5 cm,则其绝对误差限为 0.5 cm |
| 相对误差( e r ∗ e^*_ {r} er∗) | 绝对误差 精确值 ,即: e r ∗ = e ∗ x = x ∗ − x x \frac{绝对误差}{精确值},即:e^*_ {r}=\frac{e^*}{x}=\frac{x^*-x}{x} 精确值绝对误差,即:er∗=xe∗=xx∗−x 实际中精确值 x 是未知的,故常用 绝对误差 近似值 ,即: e r ∗ = e ∗ x ∗ = x ∗ − x x ∗ \frac{绝对误差}{近似值} ,即:e^*_ {r}=\frac{e^*}{x^*}=\frac{x^*-x}{x^*} 近似值绝对误差,即:er∗=x∗e∗=x∗x∗−x | 当 e r ∗ e^*_ {r} er∗ 较小时,此时 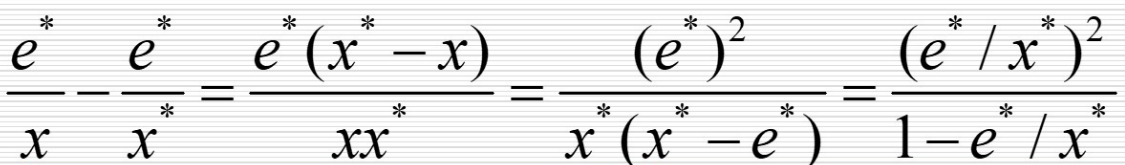 是 e r ∗ 的平方项级,故可以忽略不计,所以可以使用 e ∗ x ∗ 代替 e ∗ x 是 e^*_ {r} 的平方项级,故可以忽略不计,所以可以使用 \frac{e^*}{x^*} 代替 \frac{e^*}{x} 是er∗的平方项级,故可以忽略不计,所以可以使用x∗e∗代替xe∗ 是 e r ∗ 的平方项级,故可以忽略不计,所以可以使用 e ∗ x ∗ 代替 e ∗ x 是 e^*_ {r} 的平方项级,故可以忽略不计,所以可以使用 \frac{e^*}{x^*} 代替 \frac{e^*}{x} 是er∗的平方项级,故可以忽略不计,所以可以使用x∗e∗代替xe∗ |
| 相对误差限( ε r ∗ ε^*_ {r} εr∗) | 相对误差的上界 ε r ∗ ε^*_ {r} εr∗,即: ε r ∗ = ε ∗ ∣ x ∗ ∣ ε^*_ {r} = \frac{ε^*}{|x^*|} εr∗=∣x∗∣ε∗ | 测量某物品的长度为 20 ± 0.5 cm,则其相对误差限为 2.5% |
| 有效数字 | 示例 | |
|---|---|---|
| 定义 |  | 对于 Π=3.1415926… ,x* = 3.14有3位有效数字;x* = 3.1416 则有5为有效数字;而 x* = 3.1415 则只有4为有效数字,其误差超过了5所在位置的半个单位,而不超过1所在的位置的半个单位,故只有4位有效数字。 |
| 科学计数表示 |  | 12300 有5位有效数字,如果写成 1.23 × 104 则只有3位有效数字。 |
| 定理 |  |  |
1.2.3 数值运算的误差估计
| 函数 | (绝对)误差限 ε ∗ ( f ) ≈ ε^*( f )≈ ε∗(f)≈ | 相对误差限 ε r ∗ ( f ) ≈ ε^*_r( f )≈ εr∗(f)≈ |
|---|---|---|
| 一元函数 f(x) | | f(x)’ | ε*(x) | ε*( f(x) ) / f(x) |
| 多元函数 f(x1, …, xn) | ∑ 1 n ∣ ∂ f ∂ x i ∣ ε ∗ ( x i ) \sum_1^n |\frac{\partial f}{\partial x_i}| ε^*(x_i) 1∑n∣∂xi∂f∣ε∗(xi) | ε*( f(x1, …, xn) ) / f(x1, …, xn) |
示例:

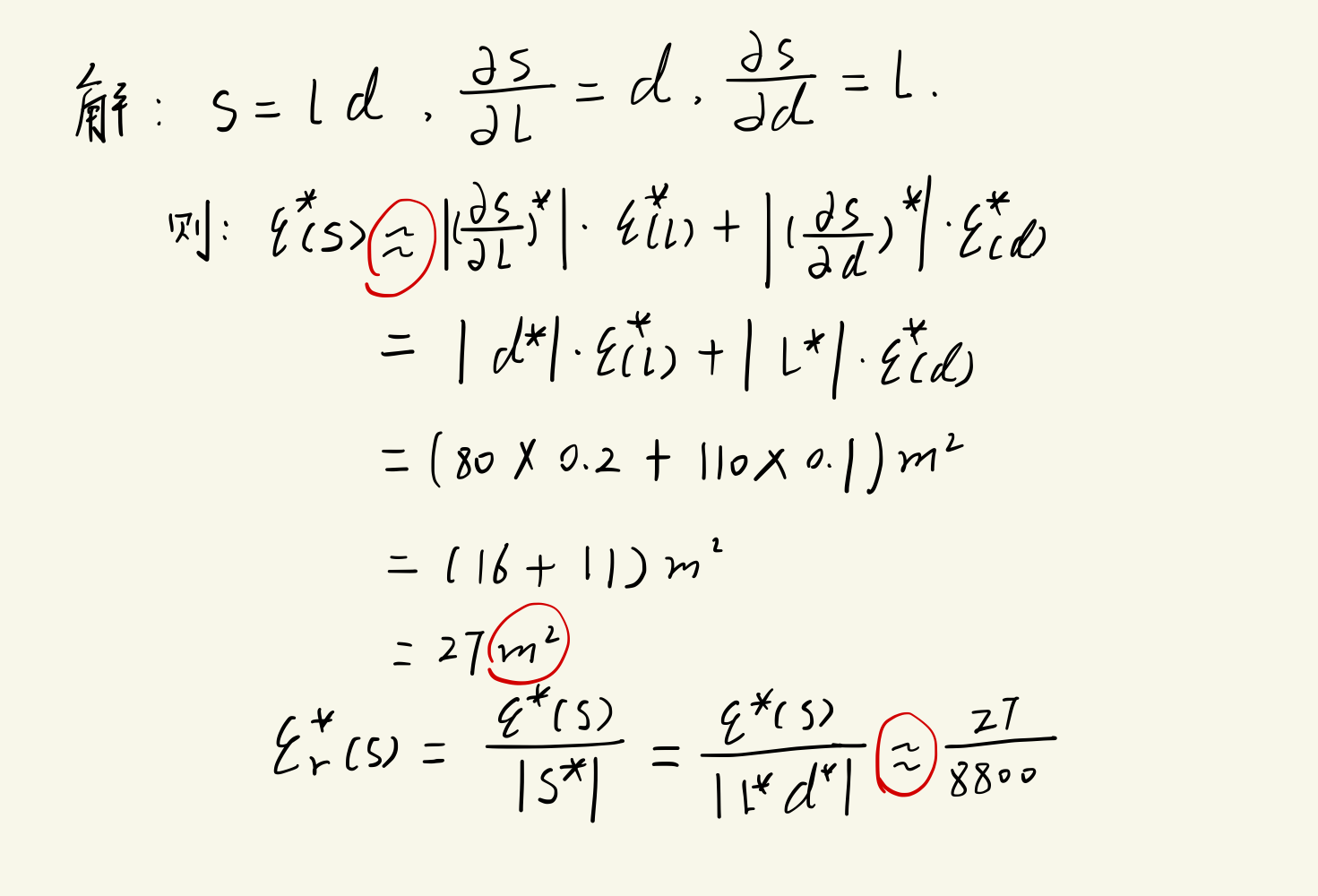
1.3 误差定性分析和避免误差危害
1.3.1 算法的数值稳定性
| 问题 | 描述 |
|---|---|
| 不稳定算法 |  |
| 病态方程组 |  |
1.3.3 避免误差危害
| 问题 | 描述 | 措施 |
|---|---|---|
| 大数吃小数 |  |  |
| 相近数相减 |  |  例如: 1 − c o s ( ε ) = 2 s i n 2 ( ε 2 ) ; 例如:1 - cos(ε) = 2 sin^2(\frac{ε}{2}) ; 例如:1−cos(ε)=2sin2(2ε); 例如: 1 − c o s ( ε ) = 2 s i n 2 ( ε 2 ) ; 例如:1 - cos(ε) = 2 sin^2(\frac{ε}{2}) ; 例如:1−cos(ε)=2sin2(2ε);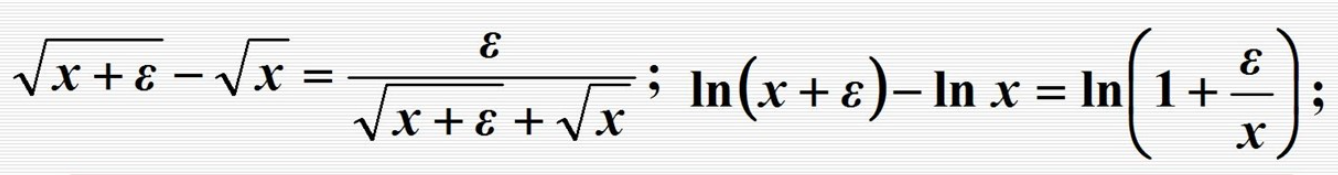 |
| 除小数和乘大数 | 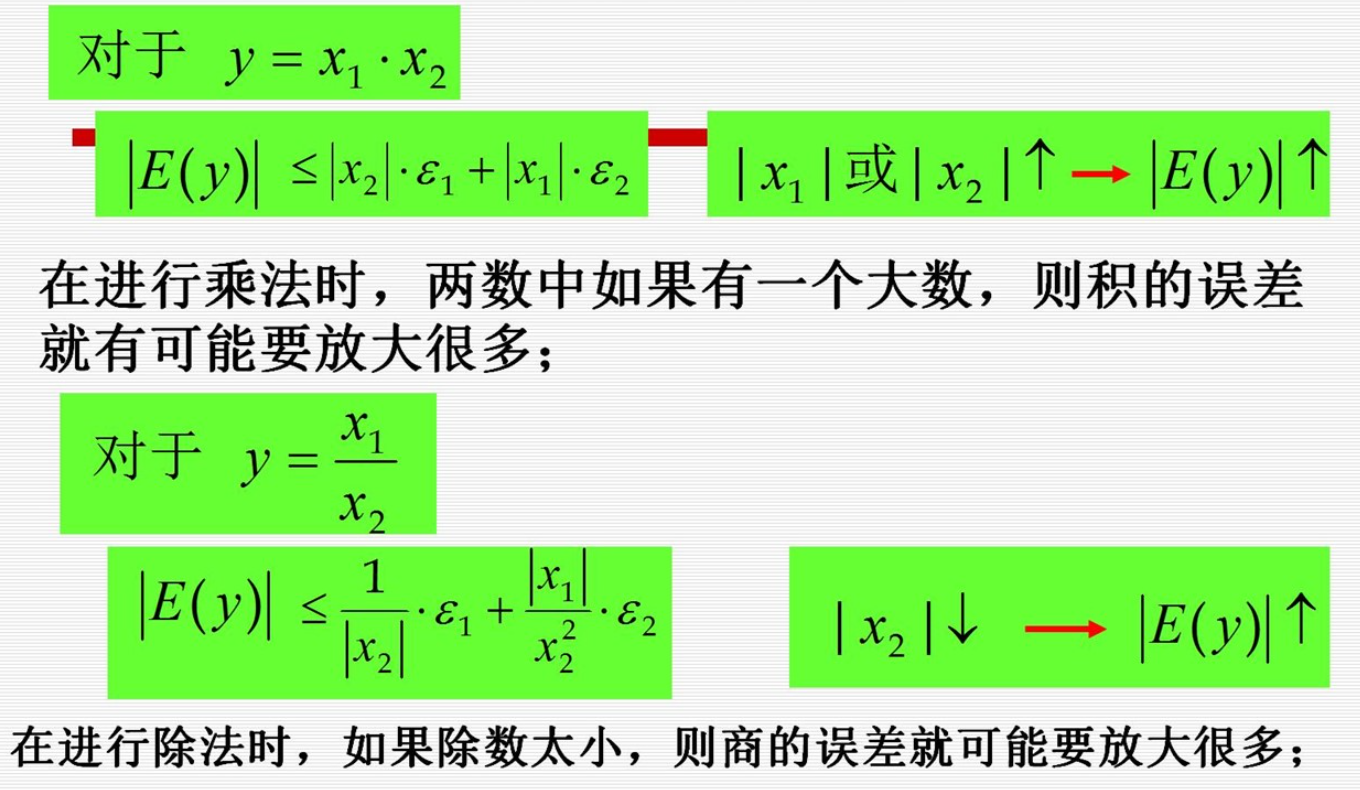 | 尽量避免 |
1.4 数值计算中算法设计的技术
| 算法 | 示例 |
|---|---|
| 快速幂算法 |  |
| 秦九韶算法 |  |
1.5 习题
1.5.1 判断题
- 解对数据的微小变化高度敏感是病态的。【对】
- 高精度运算可以改善问题的病态性。【错,病态是问题本身固有的,无法通过提高精度运算来改善】
- 无论问题是否病态,只要算法稳定都能得到好的近似值。【错,只有良态情况下,稳定的算法才有可能得到好的近似值】
- 用一个稳定的算法计算良态问题一定会得到好的近似值。【错,得到好的近似值还与初始值的选取有关,例如:牛顿法】
- 用一个收敛的迭代法计算良态问题一定会得到好的近似值。【错,得到好的近似值还与初始值的选取有关,例如:牛顿法】
- 两个相近数相减必然会使有效数字损失。【错,只是大多情况下会使有效数字损失】
- 计算机上将1000个数量级不同的数相加,不管次序如何结果都是样的。【错,可能发生大数吃小数情况】
1.5.2 计算题
- 设 x > 0,x 的相对误差为δ,求ln x的误差。
- 设 x 的相对误差为2%,求 xn 的相对误差。
- 下列各数都是经过四舍五入得到的近似数,即误差限不超过最后一位的半个单位,试指出它们是几位有效数字:
x 1 ∗ x^*_1 x1∗= 1.1021, x 2 ∗ x^*_2 x2∗= 0.031, x 3 ∗ x^*_3 x3∗= 385.6, x 4 ∗ x^*_4 x4∗= 56.430, x 5 ∗ x^*_5 x5∗=7 × 1.0 - 求下列各近似值的误差限:
(1) x 1 ∗ + x 2 ∗ + x 4 ∗ x^*_1+x^*_2+x^*_4 x1∗+x2∗+x4∗
(2) x 1 ∗ x 2 ∗ x 3 ∗ x^*_1x^*_2x^*_3 x1∗x2∗x3∗
(3) x 2 ∗ / x 4 ∗ x^*_2/x^*_4 x2∗/x4∗
其中 x 1 ∗ , x 2 ∗ , x 3 ∗ , x 4 ∗ x^*_1,x^*_2,x^*_3,x^*_4 x1∗,x2∗,x3∗,x4∗均为第3题所给的数。 - 计算球体积要使相对误差限为1%,问度量半径R时允许的相对误差限是多少?
- 正方形的边长大约为100 cm,应怎样测量才能使其面积误差不超过1 cm2 ?
- 计算 f = ( 2 − 1 ) 6 f=(\sqrt{2}-1)^6 f=(2−1)6,取 2 ≈ 1.4 \sqrt{2}≈1.4 2≈1.4,利用下列等式计算,哪一个得到的结果最好?
1 ( 2 + 1 ) 6 , ( 3 − 2 2 ) 3 \frac{1}{(\sqrt{2}+1)^6},(3-2\sqrt{2})^3 (2+1)61,(3−22)3
1 ( 3 + 2 2 ) 3 , 99 − 70 2 \frac{1}{(3+2\sqrt{2})^3},99-70\sqrt{2} (3+22)31,99−702



第2章 插值法
2.2 拉格朗日插值
2.3 牛顿插值
2.4 埃尔米特插值
2.5 分段低次插值
2.6 三次样条插值
第3章 函数逼近与快速傅里叶变换
3.4 曲线拟合的最小二乘法
第4章 数值积分与数值微分
4.1 数值积分概论
4.2 牛顿-柯特斯公式
4.3 复合求积公式
4.4 龙贝格求积公式
4.5 自适应积分方法
4.6 高斯求积公式
第5章 解线性方程组的直接方法
5.2 高斯消去法
5.3 矩阵三角分解法
5.4 向量和矩阵范数
5.5 误差分析
第6章 解线性方程组的迭代法
6.2 雅可比迭代法与高斯-塞德尔迭代法
6.3 超松弛迭代法
第7章 非线性方程与方程组的数值解法
7.1 方程求根与二分法
7.2 不动点迭代法及其收敛性
7.3 迭代收敛的加速方法
7.4 牛顿法
第9章 常微分方程初值问题数值解法
9.2 简单的数值方法
相关文章:

科学与工程计算基础(数值计算)知识点总结
数值计算 第1章 概论1.2 数值计算中的误差1.2.1 误差的来源和分类1.2.2 误差与有效数字1.2.3 数值运算的误差估计 1.3 误差定性分析和避免误差危害1.3.1 算法的数值稳定性1.3.3 避免误差危害 1.4 数值计算中算法设计的技术1.5 习题1.5.1 判断题1.5.2 计算题 第2章 插值法2.2 拉…...
oracle查询开始时间和结束时间之间的连续月份
SELECT TO_CHAR(ADD_MONTHS(TO_DATE(2023-01,YYYY-MM), ROWNUM - 1), YYYY-MM) AS fmonth FROM DUALCONNECT BY ROWNUM < CEIL(MONTHS_BETWEEN(TO_DATE(2023-11, YYYY-MM), TO_DATE(2023-01,YYYY-MM))1)...

通过 python 脚本迁移 Redis 数据
背景 需求:需要将的 Redis 数据迁移由云厂商 A 迁移至云厂商 B问题:云版本的 Redis 版本不支持 SYNC、MIGRATE、BGSAVE 等命令,使得许多工具用不了(如 redis-port) 思路 (1)从 Redis A 获取所…...
nodejs之express学习(1)
安装 npm i express使用 // 导入 const express require(express) // 创建应用 const app express() // 创建路由 app.get(/home,(req,res)>{res.end("hello express") }) app.listen(3000,()>{console.log("服务已启动~") })路由的介绍 什么是…...

【LeetCode】121. 买卖股票的最佳时机
121. 买卖股票的最佳时机 难度:简单 题目 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获…...
Vue3-VueRouter4路由语法解析
1.创建路由实例由createRouter实现 2.路由模式 1)history模式使用createWebHistory():地址栏不带# 2)hash模式使用createWebHashHistory():地址栏带# 3)参数是基础路径,默认/ 括号里的就是设置路径的前…...
ChromeDriver最新版本下载与安装方法
关于ChromeDriver最新下载地址:https://googlechromelabs.github.io/chrome-for-testing/ 下载与安装 setp1:查看Chrome浏览器版本 首先,需要检查Chrome浏览器的版本。请按照以下步骤进行: 打开Chrome浏览器。 点击浏览器右上角…...
illuminate/database 使用 四
文档:Hyperf Database: Getting Started - Laravel 10.x - The PHP Framework For Web Artisans 因为hyperf使用illuminate/database,所以按照文章,看illuminate/database代码实现。 一、读写分离 根据文档读写的host可以分开。设置读写分…...
Spring面向切面编程(AOP);Spring控制反转(IOC);解释一下Spring AOP里面的几个名词;Spring 的 IoC支持哪些功能
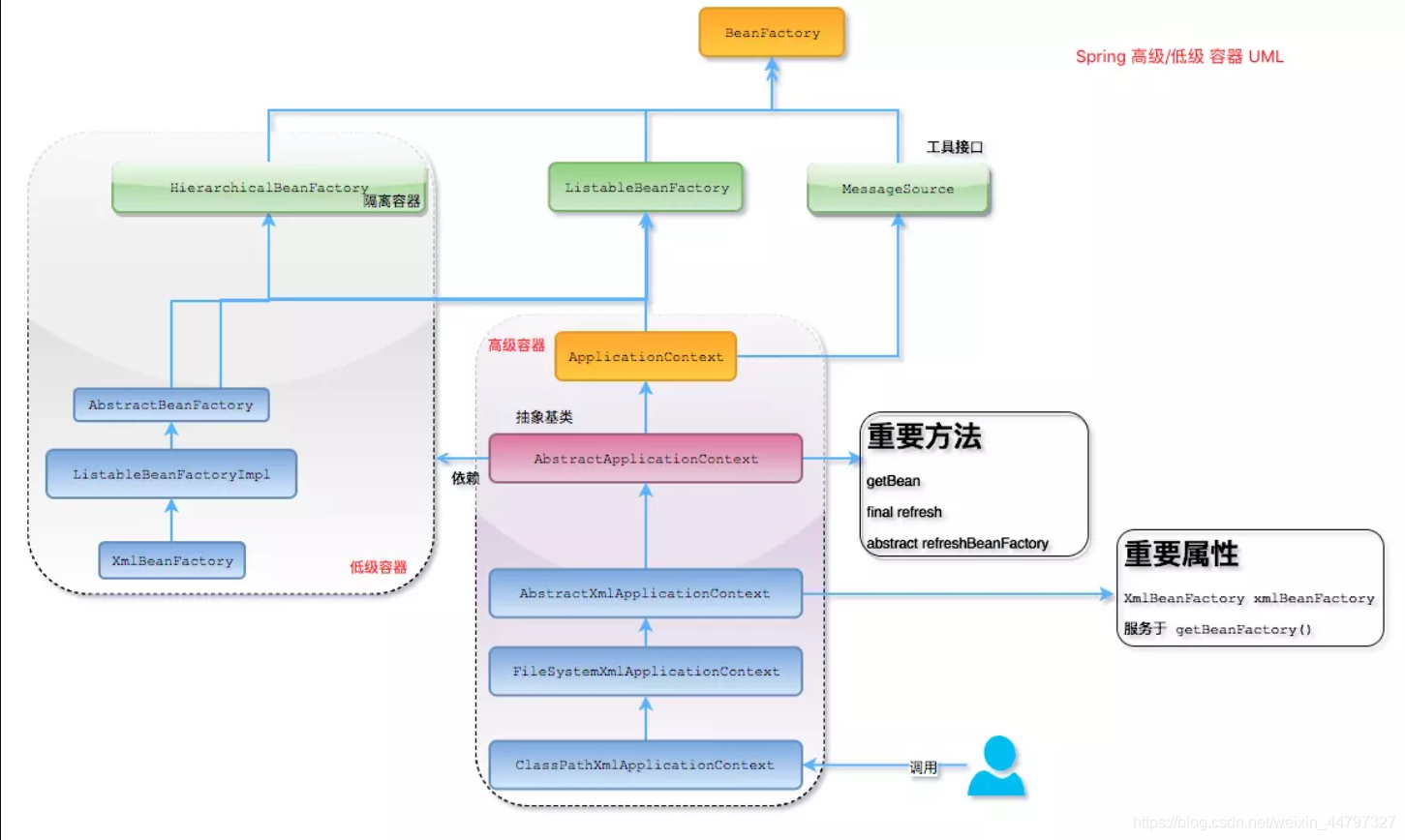
文章目录 Spring面向切面编程(AOP)什么是AOPSpring AOP and AspectJ AOP 的区别?Spring AOP中的动态代理如何理解 Spring 中的代理?解释一下Spring AOP里面的几个名词Spring在运行时通知对象Spring切面可以应用5种类型的通知:什么是切面 Aspe…...

vatee万腾的科技征途:Vatee独特探索的数字化力量
在数字化时代的浪潮中,Vatee万腾以其独特的科技征途成为引领者。公司在数字化领域的探索之路不仅是技术的创新,更是一种对未知的勇敢涉足,是对新时代的深刻洞察和积极实践。 Vatee万腾通过独特的探索,展示了在数字化征途上的创新力…...

MySQL学习day03
一、SQL图形化界面工具 常用比较常用的图形化界面有sqlyog、mavicat、datagrip datagrip工具使用相当方便,功能比前面两种都要强大。 DataGrip工具的安装和使用请查看这篇文档:DataGrip 安装教程 DML-介绍 DML全称是Data Manipulation Language(数据…...

《QT从基础到进阶·三十七》QWidget实现左侧导航栏效果
NavigationBarPlugin插件类实现了对左侧导航栏的管理,我们可以在导航栏插件中添加界面,并用鼠标点击导航栏能够切换对应的界面。 源码在文章末尾 实现效果如下: NavigationBarPlugin实现的接口如下: class NAVIGATIONBAR_EXP…...

sftp学习
什么是sftp? sftp的简单操作 远程连接 int RobostSftp::Init(QString ip,QString port,QString user_name, QString user_password) { int rc;session ssh_new();if (!session) {fprintf(stderr, "ssh initialization failed\n");// return 1…...

C++之STL库:string类(用法列举和总结)
前言 大家在学习STL库的时候一定要学会看英文文档,俗话说熟能生巧,所以还得多练!在使用string类之前,要包含头文件#include <string>和using namespace std; 文档链接:string - C Reference 一、string——构造…...
小程序中的大道理--综述
前言 以下将用一个小程序来探讨一些大道理, 这些大道理包括可扩展性, 抽象与封装, 可维护性, 健壮性, 团队合作, 工具的利用, 可测试性, 自顶向下, 分而治之, 分层, 可读性, 模块化, 松耦合, MVC, 领域模型, 甚至对称性, 香农的信息论等等. 为什么不用大程序来说大道理呢? …...

tlais智能学习辅助系统-修改部门功能实现
学习黑马程序员的JavaWeb课程,自己写的部门信息修改部分程序 控制层: //DeptController.java /** * 根据ID查询部门信息 * param id * return */ GetMapping("/{id}") public Result select(PathVariable Integer id){log.info("查询id…...
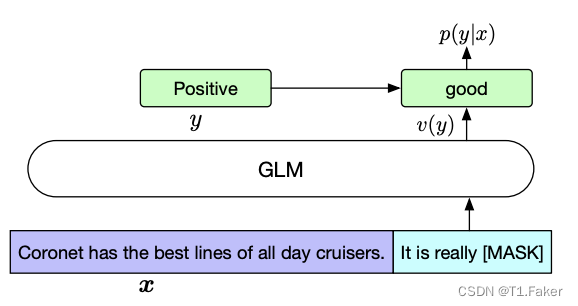
GLM: 自回归空白填充的多任务预训练语言模型
当前,ChatGLM-6B 在自然语言处理领域日益流行。其卓越的技术特点和强大的语言建模能力使其成为对话语言模型中的佼佼者。让我们深入了解 ChatGLM-6B 的技术特点,探索它在对话模型中的创新之处。 GLM: 自回归空白填充的多任务预训练语言模型 ChatGLM-6B 技…...

函数递归所应满足的条件
1.递归的概念 递归是学习C语⾔函数绕不开的⼀个话题,那什么是递归呢? 递归其实是⼀种解决问题的⽅法,在C语⾔中,递归就是函数⾃⼰调⽤⾃⼰。 递归的思想: 把⼀个⼤型复杂问题层层转化为⼀个与原问题相似,但…...

Python入职某新员工大量使用Lambda表达式,却被老员工喷是屎山
Python中Lambda表达式是一种简洁而强大的特性,其在开发中的使用优缺点明显,需要根据具体场景权衡取舍。 Lambda表达式的优点之一是它的紧凑语法,适用于一些短小而简单的函数。这种形式使得代码更为精炼,特别在一些函数式编程场景中,Lambda表达式可以提高代码的表达力。此外…...
Android Bitmap保存成至手机图片文件,Kotlin
Android Bitmap保存成至手机图片文件,Kotlin fun saveBitmap(name: String?, bm: Bitmap) {val savePath Environment.getExternalStoragePublicDirectory(Environment.DIRECTORY_PICTURES).toString()if (!Files.exists(Paths.get(savePath))) {Log.d("保存文…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...
