力扣hot100 最大子数组和 动态规划 分治 无后效性 子问题划分
👨🏫 题目地址

无后效性
为了保证计算子问题能够按照顺序、不重复地进行,动态规划要求已经求解的子问题不受后续阶段的影响。这个条件也被叫做「无后效性」。换言之,动态规划对状态空间的遍历构成一张有向无环图,遍历就是该有向无环图的一个拓扑序。有向无环图中的节点对应问题中的「状态」,图中的边则对应状态之间的「转移」,转移的选取就是动态规划中的「决策」。
关键 1:理解题意
题目要我们找出和最大的连续子数组的值是多少,「连续」是关键字,连续很重要,不是子序列。
题目只要求返回结果,不要求得到最大的连续子数组是哪一个。这样的问题通常可以使用「动态规划」解决。
关键 2:如何定义子问题(如何定义状态)
设计状态思路:把不确定的因素确定下来,进而把子问题定义清楚,把子问题定义得简单。动态规划的思想通过解决了一个一个简单的问题,进而把简单的问题的解组成了复杂的问题的解。
🍻 DP
public class Solution {public int maxSubArray(int[] nums) {int n = nums.length;int[] f = new int[n];// 记录nums[i]结尾的最大连续数组和f[0] = nums[0];int ans = f[0];for (int i = 1; i < n; i++){f[i] = Math.max(f[i - 1] + nums[i], nums[i]);ans = Math.max(ans, f[i]);}return ans;}
}🍻 DP优化空间
public class Solution {public int maxSubArray(int[] nums) {int pre = 0;int res = nums[0];for (int num : nums) {pre = Math.max(pre + num, num);res = Math.max(res, pre);}return res;}
}🍻 分治
public class Solution {public int maxSubArray(int[] nums) {int len = nums.length;if (len == 0) {return 0;}return maxSubArraySum(nums, 0, len - 1);}private int maxCrossingSum(int[] nums, int left, int mid, int right) {// 一定会包含 nums[mid] 这个元素int sum = 0;int leftSum = Integer.MIN_VALUE;// 左半边包含 nums[mid] 元素,最多可以到什么地方// 走到最边界,看看最值是什么// 计算以 mid 结尾的最大的子数组的和for (int i = mid; i >= left; i--) {sum += nums[i];if (sum > leftSum) {leftSum = sum;}}sum = 0;int rightSum = Integer.MIN_VALUE;// 右半边不包含 nums[mid] 元素,最多可以到什么地方// 计算以 mid+1 开始的最大的子数组的和for (int i = mid + 1; i <= right; i++) {sum += nums[i];if (sum > rightSum) {rightSum = sum;}}return leftSum + rightSum;}private int maxSubArraySum(int[] nums, int left, int right) {if (left == right) {return nums[left];}int mid = left + (right - left) / 2;return max3(maxSubArraySum(nums, left, mid),maxSubArraySum(nums, mid + 1, right),maxCrossingSum(nums, left, mid, right));}private int max3(int num1, int num2, int num3) {return Math.max(num1, Math.max(num2, num3));}
}
👨🏫 参考地址
相关文章:

力扣hot100 最大子数组和 动态规划 分治 无后效性 子问题划分
👨🏫 题目地址 无后效性 为了保证计算子问题能够按照顺序、不重复地进行,动态规划要求已经求解的子问题不受后续阶段的影响。这个条件也被叫做「无后效性」。换言之,动态规划对状态空间的遍历构成一张有向无环图,遍…...

C语言--每日选择题--Day28
第一题 1. 设a和b均为double型变量,且a5.5、b2.5,则表达式(int)ab/b的值是( ) A:6.500000 B:6 C:5.500000 D:6.000000 答案及解析 D 本题考查的是不同数据类型之间的变量进行运算时…...

Linux 安装 Minio 配置 HTTPS
安装 创建目录 [roott2 local]# mkdir minio [roott2 local]# cd minio [roott2 minio]# mkdir data下载 [roott2 minio]# wget https://dl.min.io/server/minio/release/linux-amd64/minio [roott2 minio]# chmod x minio # 赋权设置账号密码 minio 默认账号密码为 minio…...
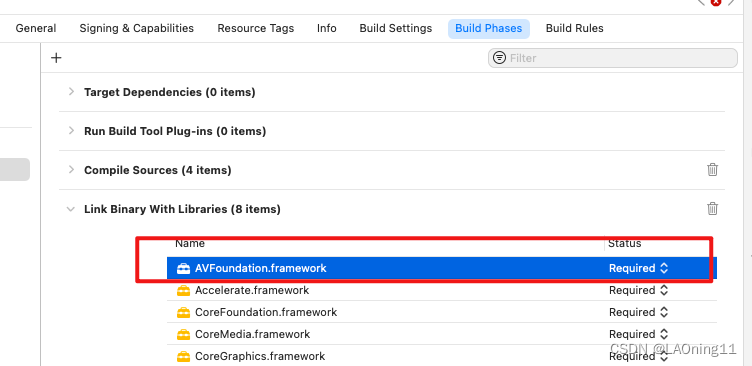
xcode opencv
1、导入报错 Undefined symbols: linker command failed with exit code 1 (use -v to see invocation) 直接添加如下图内容即可...
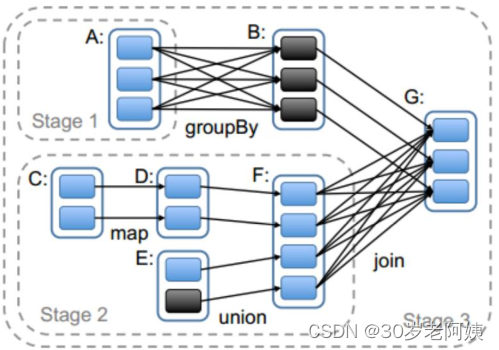
Spark---资源、任务调度
一、Spark资源调度源码 1、Spark资源调度源码过程 Spark资源调度源码是在Driver启动之后注册Application完成后开始的。Spark资源调度主要就是Spark集群如何给当前提交的Spark application在Worker资源节点上划分资源。Spark资源调度源码在Master.scala类中的schedule()中进行…...

单片机开发常见问题集合
文章目录 发送串口数据偶尔丢失字节 发送串口数据偶尔丢失字节 场景: 在STM32单片机中进行串口数据发送,在Linux/Windows上进行串口数据接收,会偶发出现接收到的数据有某些字节丢失。 分析: 在STM32中可以使用printf用于发送串口…...

Matlab 点云曲率计算(之二)
文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 之前已经讨论过许多关于计算曲率的问题,这里使用一个通过拟合三次曲面方程的方式来计算曲率,计算过程如下图所示: 二、实现代码 %********...

C++11的原子变量
C11提供了一个原子类型std::atomic<T>,可以使用任意类型作为模板参数,C11内置了整型的原子变量,可以更方便的使用原子变量,使用原子变量就不需要使用互斥量来保护该变量了,用起来更简洁。例如,要做一…...
 考试试卷)
北京交通大学 计算机网络体系与协议(研) 考试试卷
计算机网络体系与协议2023年期末考试 时长:120分钟 学院: 学号: 姓名: 一、简答题(每题5分) 1.简述公开密钥密码体制的工作原理…...
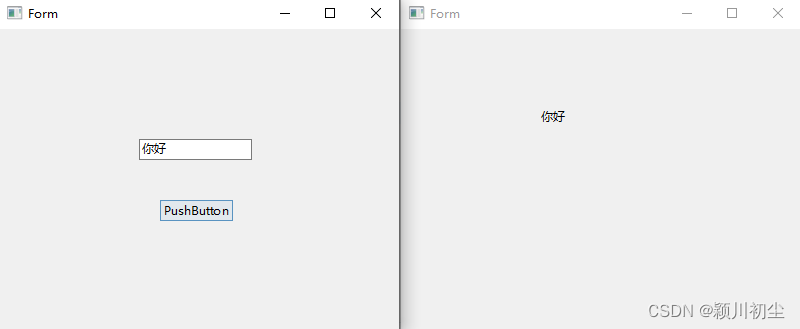
python之pyqt专栏7-信号与槽3
在上一篇文章中python之pyqt专栏6-信号与槽2-CSDN博客中,我们可以了解到对象可以使用内置信号,这些信号来自于类定义或者继承过来的。我们可以对这些信号可以通过connect连接槽函数。 需求 现在有一个需求,有两个UI界面“untitled.ui”和“u…...

高噪点灰度图目标粗定位CoraseLocation
高噪点的灰度图目标粗定位 /* ** name: CoraseLocation ** brief: 粗定位 ** param:[in] srcGray 灰度图() ** param:[in] box 目标尺寸(像素) ** param:[ou] roi 目标定位结果 ** return: true成功,false…...
)
Android:Google三方库之Firebase集成详细步骤(二)
Analytics分析 1、将 Firebase 添加到您的 Android 项目(如果尚未添加),并确保在 Firebase 项目中启用了 Google Analytics(分析): 如果您要创建新的 Firebase 项目,请在项目创建过程中启用 G…...

java使用freemarker模板生成html,再生成pdf
1.freemarker模板生成html 添加Maven依赖 在pom.xml文件中添加以下依赖: <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-freemarker</artifactId> </dependency>创建Freemarker…...

图解系列--Web服务器,Http首部
1.用单台虚拟主机实现多个域名 HTTP/1.1 规范允许一台 HTTP 服务器搭建多个 Web 站点。。比如,提供 Web 托管服务(Web Hosting Service)的供应商,可以用一台服务器为多位客户服务,也可以以每位客户持有的域名运行各自不…...
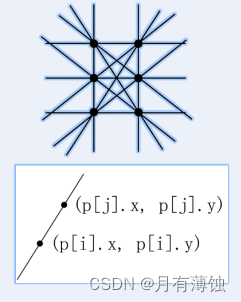
直线(蓝桥杯)
直线 题目描述 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 在平面直角坐标系中,两点可以确定一条直线。如果有多点在一条直线上, 那么这些点中任意两点确定的直线是同一条。 给定平面上 2 3 个…...

Android:从源码看FragmentManager如何工作
一个Activity中,在某一个容器中,更换不同的Fragment,从而显示不同的界面,这个场景相信大家已经非常熟悉了,也知道Activity是通过FragmentManager来管理嵌入的Fragments的,所以今天就来看看FragmentManager是…...
LabVIEW通过编程将图形类控件的X轴显示为时间戳
LabVIEW通过编程将图形类控件的X轴显示为时间戳 每个版本的LabVIEW中都有属性节点,可以以编程方式调整X轴和Y轴格式。对于不同版本的LabVIEW,这些属性节点无法在同一个位置找到。请参阅以下部分,了解特定版本LabVIEW的相关属性节点的位置。 …...
Spring Boot进行单元测试,一个思路解决重启低效难题!
所谓单元测试就是对功能最小粒度的测试,落实到JAVA中就是对单个方法的测试。 junit可以完成单个方法的测试,但是对于Spring体系下的web应用的单元测试是无能为力的。因为spring体系下的web应用都采用了MVC三层架构,依托于IOC,层级…...

c/c++ header_only 头文件实现的关键点
header_only 头文件实现的关键点 ------------------------------------------------------------------------- author: hjjdebug date: 2023年 11月 28日 星期二 16:58:38 CST descriptor: header_only 头文件实现的关键点1. 对外声明的函数必需加上inline, 消除连接的歧义…...
:通过docker安装redis)
Linux(CentOS7.5):通过docker安装redis
一、准备配置文件 在宿主机,准备映射配置文件的目录下,运行如下: wget http://download.redis.io/redis-stable/redis.conf二、安装 docker run \ --restartalways \ --log-opt max-size100m \ --log-opt max-file2 \ -p 6380:6379 \ -v /opt…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...
