广州华锐视点:基于VR元宇宙技术开展法律法规常识在线教学,打破地域和时间限制
随着科技的飞速发展,人类社会正逐渐迈向一个全新的时代——元宇宙。元宇宙是一个虚拟的、数字化的世界,它将现实世界与数字世界紧密相连,为人们提供了一个全新的交流、学习和娱乐平台。在这个充满无限可能的元宇宙中,法律知识同样具有重要的意义。本文将探讨如何在元宇宙中开展法律法规常识在线教学,帮助人们更好地适应这个新时代。
在元宇宙中,人们可以自由地创造、交易和拥有虚拟财产,这就涉及到知识产权、合同法等法律问题。此外,元宇宙中的虚拟身份和隐私保护也是一个重要的法律议题。因此,在元宇宙中开展法律法规常识在线教学,需要关注这些现实与虚拟交织的法律问题。

元宇宙中的法律法规常识在线教学方式
1.线上讲座和研讨会
借助元宇宙中的虚拟现实技术,我们可以组织线上讲座和研讨会,邀请法律专家和学者为参与者讲解元宇宙中的法律知识。这种方式可以让更多的人参与到法律知识的学习中来,打破地域和时间的限制。
2.互动式法律教育游戏
通过开发互动式法律教育游戏,让参与者在游戏中体验元宇宙中的法律问题,从而更好地理解和掌握法律知识。这种方式既有趣又实用,能够吸引更多的人参与学习。
3.法律知识问答平台
在元宇宙中建立一个法律知识问答平台,让用户可以提问、回答和分享法律知识。这种方式可以激发用户学习法律知识的积极性,形成一个良好的学习氛围。
元宇宙中的法律法规常识在线教学内容
知识产权法
在元宇宙中,用户可以创作各种虚拟作品,如虚拟艺术品、音乐、电影等。因此,知识产权法是元宇宙中的一个重要法律议题。我们需要讲解知识产权法的基本原理,以及在元宇宙中的实际应用。
合同法
在元宇宙中,用户可以自由地购买、出售和交换虚拟财产。这就需要了解合同法的相关知识,以确保交易的合法性和有效性。我们需要讲解合同法的基本概念、合同的订立和履行等内容。
虚拟身份和隐私保护
在元宇宙中,用户的虚拟身份和隐私信息可能会受到侵犯。因此,我们需要讲解虚拟身份和隐私保护的相关法律法规,以及如何保护自己的虚拟身份和隐私信息。
【VR虚拟现实开发公司推荐广州华锐视点,拥有16年经验的老牌VR内容制作公司,为客户提供3D/VR/AR技术服务,多年来已合作600多家企业,与清华北大、故宫文物、正大集团、汽车之家等均有深入合作,形成400多项整体解决方案,满足客户更多元的需求。】
相关文章:

广州华锐视点:基于VR元宇宙技术开展法律法规常识在线教学,打破地域和时间限制
随着科技的飞速发展,人类社会正逐渐迈向一个全新的时代——元宇宙。元宇宙是一个虚拟的、数字化的世界,它将现实世界与数字世界紧密相连,为人们提供了一个全新的交流、学习和娱乐平台。在这个充满无限可能的元宇宙中,法律知识同样…...
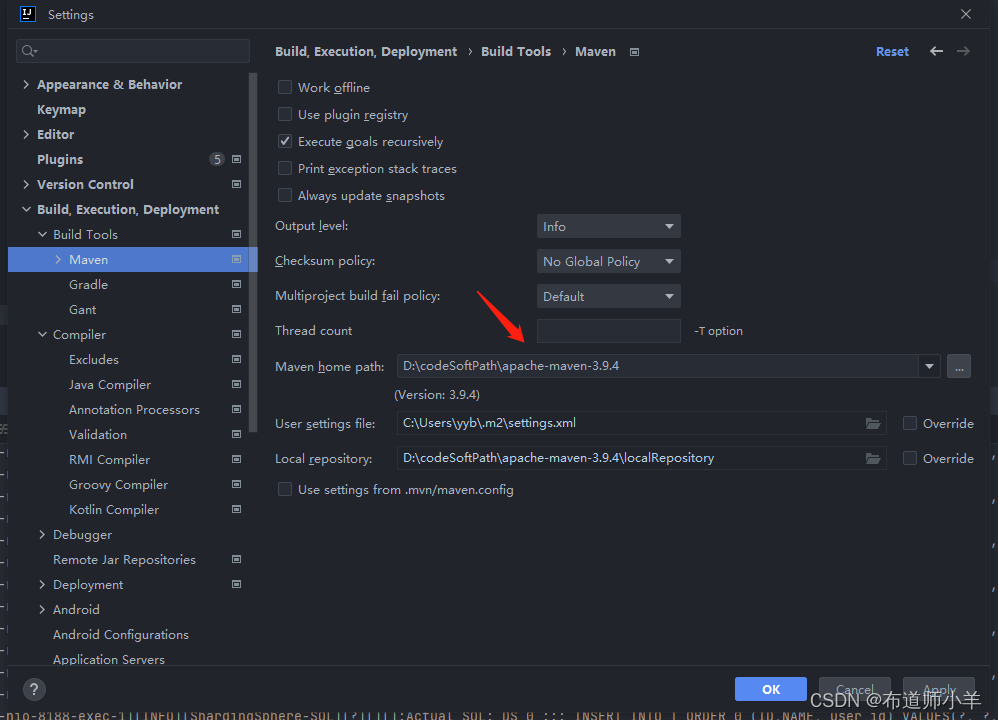
Maven——Maven使用基础
1、安装目录分析 1.1、环境变量MAVEN_HOME 环境变量指向Maven的安装目录,如下图所示: 下面看一下该目录的结构和内容: bin:该目录包含了mvn运行的脚本,这些脚本用来配置Java命令,准备好classpath和相关…...
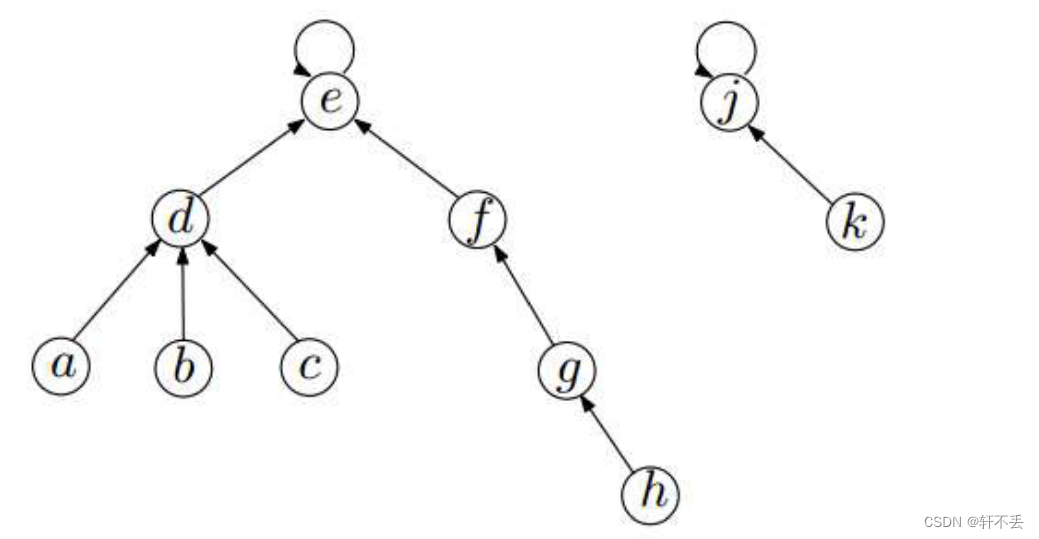
U4_2:图论之MST/Prim/Kruskal
文章目录 一、最小生成树-MST生成MST策略一些定义 思路彩蛋 二、普里姆算法(Prim算法)思路算法流程数据存储分析 伪代码时间复杂度分析 三、克鲁斯卡尔算法(Kruskal算法)分析算法流程并查集-Find-set 伪代码时间复杂度分析 一、最…...

springboot 注解@JsonInclude
修饰 实体属性or实体类 //枚举值:ALWAYS,NON_NULL,NON_ABSENT,NON_EMPTY,NON_DEFAULT,CUSTOM,USE_DEFAULTS JsonInclude(Include.NON_EMPTY)//将该标记放在属性上,如果该属性为NULL则不参与序列化 //如果放在类上边,那对这个类的全部属性起作用 Inclu…...

Python 中文完整教程目录
Python 教程 Python 是一门易于学习、功能强大的编程语言。它提供了高效的高级数据结构,还能简单有效地面向对象编程。Python 优雅的语法和动态类型以及解释型语言的本质,使它成为多数平台上写脚本和快速开发应用的理想语言。 Python 官网(…...

C/C++---------------LeetCode第35. 搜索插入位置
插入的位置 题目及要求二分查找在main内使用 题目及要求 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 示例 1: …...

网络安全--基于Kali的网络扫描基础技术
文章目录 1. 标准ICMP扫描1.1使用Ping命令1.1.1格式1.1.2实战 1.2使用Nmap工具1.2.1格式1.2.2实战1.2.2.1主机在线1.2.2.2主机不在线 1.3使用Fping命令1.3.1格式1.3.2实战 2. 时间戳查询扫描2.1格式2.2实战 3. 地址掩码查询扫描3.1格式3.2实战 2. TCP扫描2.1TCP工作机制2.2TCP …...
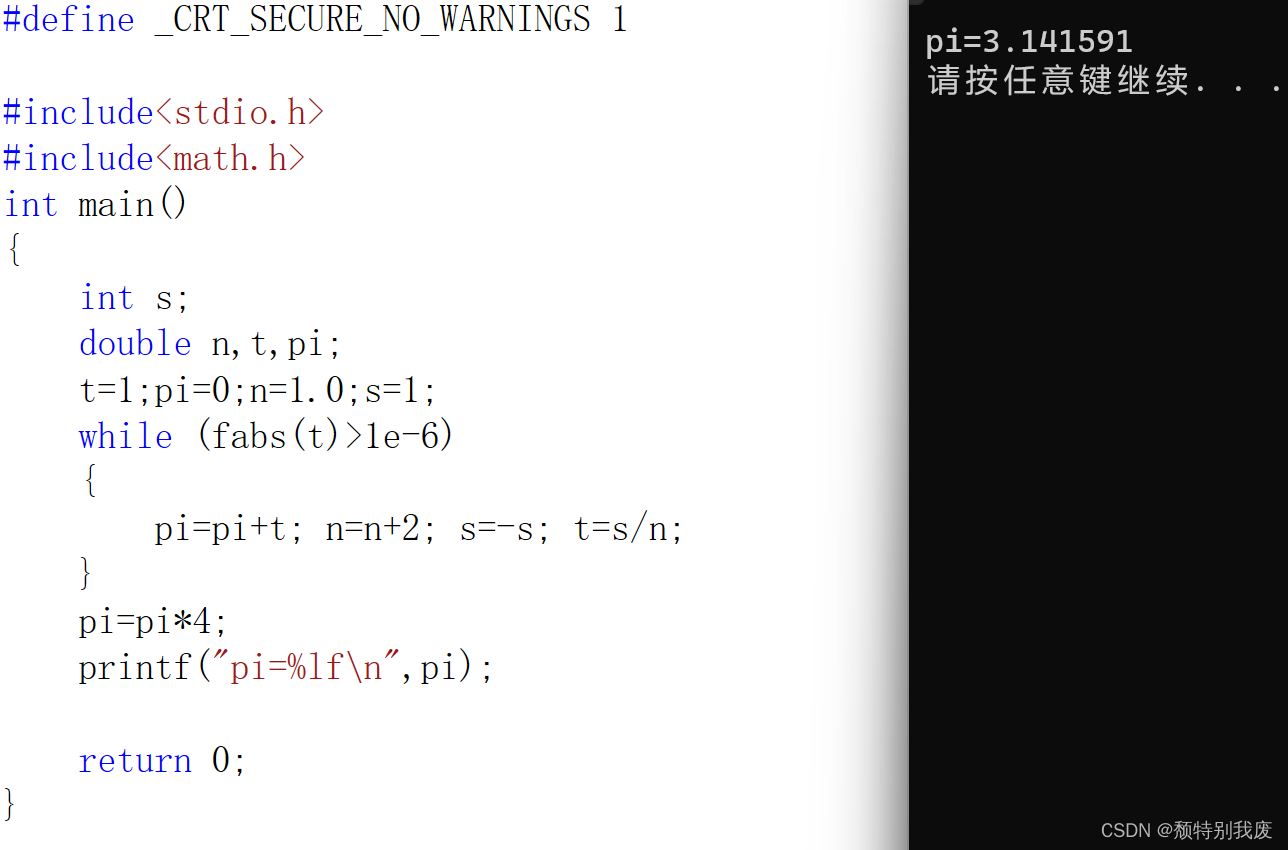
C语言——求π的近似值
#define _CRT_SECURE_NO_WARNINGS 1#include<stdio.h> #include<math.h> int main() {int s;double n,t,pi;t1;pi0;n1.0;s1;while (fabs(t)>1e-6){pipit; nn2; s-s; ts/n;}pipi*4;printf("pi%lf\n",pi);return 0; }这里是求小数点后6位——1e-6&#…...

如何使用ffmpeg转换图片格式
ffmpeg简介与图片格式介绍 windows安装ffmpeg,从如下网站下载release版本 https://www.gyan.dev/ffmpeg/builds/ ffmpeg 6.1版本仍然不支持heic的图片格式,未来可能会支持,具体见该issue: https://trac.ffmpeg.org/ticket/6521 …...

11 动态规划解最后一块石头的重量II
来源:LeetCode第1049题 难度:中等 描述:有一堆石头,用证书数组stones表示,其中stones[i]表示第i块石头的重量,每一回合,从中选出任意两块石头,然后将他们放在一起粉碎,…...
|LeetCode121. 买卖股票的最佳时机、LeetCode122. 买卖股票的最佳时机 II)
LeetCode算法题解(动态规划,股票买卖)|LeetCode121. 买卖股票的最佳时机、LeetCode122. 买卖股票的最佳时机 II
一、LeetCode121. 买卖股票的最佳时机 题目链接:121. 买卖股票的最佳时机 题目描述: 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一…...

python实验3 石头剪刀布游戏
实验3:石头剪刀布游戏 一、实验目的二、知识要点图三、实验1. 石头剪刀布2. 实现大侠个人信息 一、实验目的 了解3类基本组合数据类型。理解列表概念并掌握Python中列表的使用。理解字典概念并掌握Python中字典的使用。运用jieba库进行中文分词并进行文本词频统计。…...

米贸搜|如何设置 Facebook 转换 API + 事件重复数据删除
Facebook Pixel 可让您跟踪用户在您网站上的行为、收集再营销受众并创建相似对象。如果 Facebook 像素实现正确,它将向 FB 机器学习算法提供相关信息。 FB ML 将使用像素数据向最有可能转化的人展示您的广告。 几年来,我们可以通过 JavaScript 代码、应…...

python每日一题——11滑动窗口最大值
题目 给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。返回滑动窗口中的最大值 。 示例 1: 输入:nums [1,3,-1,-3,5,3,6,7], k 3…...
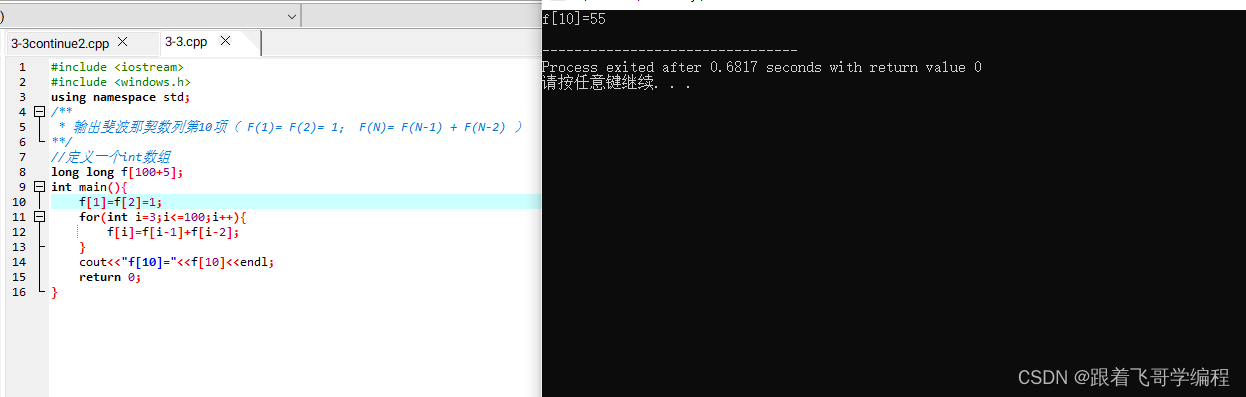
【C++ 程序设计入门基础】- 第3节-循环结构01
目录 循环结构 一、for 语句 for 循环案例 输入一个整数n,输出1~n的所有整数。 编译运行,查看输出结果 编译调试 for 循环结构语义分析 二、beak 语句 三、continue 语句 案例1: 案例2: 案例3: 循环…...

人工智能原理复习--知识表示(一)
文章目录 上一篇知识概述命题逻辑谓词逻辑谓词逻辑的应用 下一篇 上一篇 人工智能原理复习–绪论 知识概述 知识就是人类认识自然界的精神产物,是人类进行智能活动的基础。 是经过加工的信息,包括事实、信念和启发式规则。 分类: 按作用可…...

网络运维与网络安全 学习笔记2023.11.28
网络运维与网络安全 学习笔记 第二十九天 今日目标 OSPF汇总之域间路由、OSPF汇总之外部路由、OSPF链路认证 OSPF安全认证之区域认证、OSPF虚链路 OSPF汇总指域间路由 项目背景 企业内网运行多区域的OSPF网络,在R1 上存在多个不稳定的链路 R1上的不稳定链路&a…...

Rust开发——数据对象的内存布局
枚举与Sized 数据 一般数据类型的布局是其大小(size)、对齐方式(align)及其字段的相对偏移量。 1. 枚举(Enum)的布局: 枚举类型在内存中的布局通常是由编译器来确定的。不同的编译器可能有不…...

mySQL踩坑记录
1.MYSQL Workbench-8.0.27.1出现"Exception: Current profile has no WMI enabled"错误的解决方法 MYSQL Workbench-8.0.27.1出现“Exception: Current profile has no WMI enabled“错误的解决方法_赛风扥的博客-CSDN博客 C:\Program Files\MySQL\MySQL Workbench …...
【Java】使用 IDEA 快速生成 SpringBoot 模块
项目目录下新建 module 模块 在 pom.xml 更改为 spring initializr 配置之后的 pom.xml <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchem…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...
