【C++设计模式】单例模式singleton
C++ 设计模式–单例模式singleton
单例模式
单例模式是指确保一个类在任何情况下都绝对只有一个实例,并提供一个全局访问点。
优点:内存中只有一个实例,减少内存开销;避免对资源多重占用;设置全局访问点,严格控制访问。
缺点:没有接口,扩展困难;如果要扩展单例对象,只有修改代码,没有其他途径,不符合程序的开闭原则。
饿汉式单例模式
饿汉式单例模式在类加载的时候就立即初始化,并且创建单例对象。它绝对线程安全,在线程还没出现以前就实例化了,不可能存在访问安全问题。
- 优点:不用加锁就能保证线程安全。
- 缺点:内存浪费。
懒汉式单例模式
该模式的特点是类加载时没有生成单例,只有当第一次使用时才去创建这个单例。
- 优点:避免内存浪费。
- 缺点:必须加锁才能保证线程安全,加锁则会影响性能。
单例模式封装类singleton
#ifndef __RADIXUN_SINGLETION_H__
#define __RADIXUN_SINGLETION_H__namespace radixun{/*** @brief 单例模式封装类* @details T 类型* X 为了创造多个实例对应的Tag* N 同一个Tag创造多个实例索引*/
template<class T, class X = void, int N = 0>
class Singleton {
public:/*** @brief 返回单例裸指针*/static T* GetInstance() {static T v;return &v;}
};/*** @brief 单例模式智能指针封装类* @details T 类型* X 为了创造多个实例对应的Tag* N 同一个Tag创造多个实例索引*/
template<class T, class X = void, int N = 0>
class SingletonPtr {
public:/*** @brief 返回单例智能指针*/static std::shared_ptr<T> GetInstance() {static std::shared_ptr<T> v(new T);return v;}
};}#endif
相关文章:

【C++设计模式】单例模式singleton
C 设计模式–单例模式singleton 单例模式 单例模式是指确保一个类在任何情况下都绝对只有一个实例,并提供一个全局访问点。 优点:内存中只有一个实例,减少内存开销;避免对资源多重占用;设置全局访问点,严…...

CVPR 2023 精选论文学习笔记:Post-Training Quantization on Diffusion Models
基于MECE原则,我们给出以下四种分类依据: 1. 模型类型 生成模型用于生成与其训练数据相似的新数据。它们通常用于图像生成、文本生成和音乐生成等任务。语言模型用于理解和生成人类语言。它们通常用于机器翻译、聊天机器人和文本摘要等任务。其他模型用于各种任务,例如图像…...

Python基础语法之学习字符串快速格式化
Python基础语法之学习字符串快速格式化 一、代码二、效果 一、代码 # 通过f"{占位}"控制字符串快速格式化,不做精度控制 name "张三" age 13 money 12.5 text f"姓名是{name},年龄是{age},钱是{money}" print(text)二、效果 每一天都是一个…...
Ubuntu22.04 server版本关闭DHCP,手动设置ip
在Ubuntu 22.04 中,网络配置已迁移到 Netplan,因此可以使用 Netplan 配置文件来手动设置 IP 地址并关闭 DHCP。 以下是在 Ubuntu 22.04 上手动设置 IP 地址并禁用 DHCP 的步骤: 打开终端,使用 root 权限或 sudo 执行以下命令&…...

贪心算法(新坑)
贪心入门 概述: 贪心算法是一种在每一步选择中都采取当前最优解的策略,希望最终能够得到全局最优解的算法。简单来说,它会不断地做出局部最优的选择,相信通过这种选择最终能够达到全局最优。 举个例子来说明。假设你要从一个迷…...

C 语言头文件
C 语言头文件 头文件是扩展名为 .h 的文件,包含了 C 函数声明和宏定义,被多个源文件中引用共享。有两种类型的头文件:程序员编写的头文件和编译器自带的头文件。 在程序中要使用头文件,需要使用 C 预处理指令 #include 来引用它…...

MySQL中自增id用完怎么办?
MySQL中自增id用完怎么办? MySQL里有很多自增的id,每个自增id都是定义了初始值,然后不停地往上加步长。虽然自然数是没有上限的,但是在计算机里,只要定义了表示这个数的字节长度,那它就有上限。比如&#…...
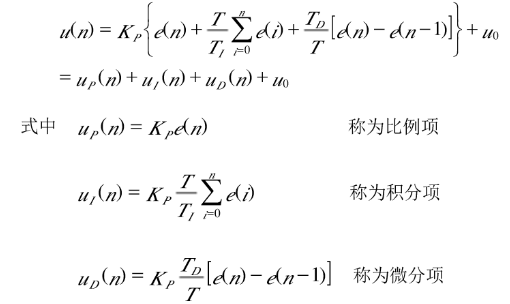
C语言常见算法
算法(Algorithm):计算机解题的基本思想方法和步骤。算法的描述:是对要解决一个问题或要完成一项任务所采取的方法和步骤的描述,包括需要什么数据(输入什么数据、输出什么结果)、采用什么结构、使…...

0-1背包的初始化问题
题目链接 这道题的状态转移方程比较易于确定。dp[i][j]表示能放前i个物品的情况下,容量为j时能放物品的数量(这道题歌曲数量对应物品数量,容量对应时间)。 技巧(收获) 二维dp数组可以视情况优化为一维dp数组…...
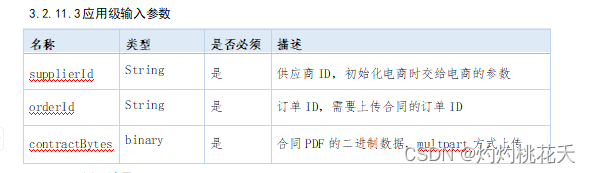
API之 要求接口上传pdf 以 合同PDF的二进制数据,multpart方式上传
实现 //时间戳13位毫秒private function getMillisecond() {list($s1,$s2) explode( ,microtime());return (float)sprintf(%.0f,(floatval($s1) floatval($s2)) * 1000);}// 组装参数private function gysscPost1($url,$data){// $data[timestamp] 1694402111964;$data[tim…...

C语言-求阶乘序列前N项和
本题要求编写程序,计算序列 1!2!3!⋯ 的前N项之和。 输入格式: 输入在一行中给出一个不超过12的正整数N。 输出格式: 在一行中输出整数结果。 输入样例: 5输出样例: 153 #include "stdio.h" int main(){int n;int sum 0;scanf("%d",&a…...
)
3:kotlin 逻辑控制(Control flow)
像其他语言一样,kotlin也有循环和逻辑控制 条件判断(Conditional expressions) kotlin使用if和when来进行条件判断 如果纠结选择if还是when,建议使用when,因为它更能提高程序的健壮性 if 普通写法 fun main() {val…...

Linux系统之一次性计划任务at命令的基本使用
Linux系统之一次性计划任务at命令的基本使用 一、at命令介绍二、at命令的使用帮助2.1 at命令的help帮助信息2.2 at命令的语法解释 三、at命令的日常使用3.1 立即执行一次性任务3.2 指定时间执行一次性任务3.3 查询计划任务3.4 其他指定时间用法3.5 删除已经设置的计划任务3.6 显…...
记录:Unity脚本的编写8.0
目录 需求分析设计GUI包含账号和密码输入栏,包括登录和注册按键添加背景音乐编写脚本控制音乐 退出按钮编写脚本 背景图片完整代码 一个小demo,登录和注册的实现(包括GUI和数据库操控) 需求分析 自行设计GUI,要求 1.包…...

OpenCV | 模版匹配
import cv2 #opencv读取的格式是BGR import numpy as np import matplotlib.pyplot as plt#Matplotlib是RGB %matplotlib inline 模版匹配 模版匹配和卷积原理很像,模版在原图像上从原点开始滑动,计算模版与(图像被模版覆盖的地方ÿ…...
【算法刷题】Day7
文章目录 283. 移动零1089. 复写零 283. 移动零 原题链接 看到题目,首先看一下题干的要求,是在原数组内进行操作,平切保持非零元素的相对顺序 这个时候我们看到了示例一: [ 0, 1, 0, 3,12 ] 这个时候输出成为了 [ 1, 3, 12, 0, …...

前端 | iframe框架标签应用
文章目录 📚嵌入方式📚图表加载显示📚100%嵌入及滑动条问题📚加载动画保留 前情提要: 计划用iframe把画好的home1.html(echarts各种图表组成的html数据大屏)嵌入整合到index.html(搭…...

linux -系统通用命令查询
有时候内网环境下,系统有些命令没有安装因此掌握一些通用的linux 命令也可以帮助我们解决一些问题查看 1.查看系统内核版本 uname -r2.查看系统版本 cat /etc/os-release3. 查看cpu 配置 lscpu4.查看内存信息 free [参数] 中各个数值的解释如下表 数值解释t…...

python炒股自动化(1),量化交易接口区别
要实现股票量化程序化自动化,就需要券商提供的API接口,重点是个人账户小散户可以申请开通,上手要简单,接口要足够全面,功能完善,首先,第一步就是要找对渠道和方法,这里我们不讨论量化…...
LeetCode(35)螺旋矩阵【矩阵】【中等】
目录 1.题目2.答案3.提交结果截图 链接: 54. 螺旋矩阵 1.题目 给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。 示例 1: 输入:matrix [[1,2,3],[4,5,6],[7,8,9]] 输出:…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...
