【点云surface】无序点云快速三角化
1 介绍
GreedyProjectionTriangulation 是一种基于局部二维投影的三维点贪婪三角剖分算法的实现。它假定局部表面光滑,不同点密度区域之间的过渡相对平滑。
GreedyProjectionTriangulation算法的基本思想是通过逐步投影点云数据到一个三角化网格上来进行重建。它首先根据给定的搜索半径找到每个点的最近邻点,然后根据这些最近邻点构建局部三角化表面。接下来,通过迭代地添加新的点并更新三角化表面,最终生成完整的三角化网格模型。
GreedyProjectionTriangulation类提供了一系列参数和方法,用于控制和定制三角化过程。一些重要的参数包括搜索半径、最小和最大角度、法向量平滑度等。此外,它还提供了一些方法来设置输入点云数据、执行重建过程并获取生成的三角化网格。
setSearchRadius(double radius):设置搜索半径。该参数定义了在找到最近邻点时所使用的搜索半径。较大的搜索半径可以包含更多的邻近点,但可能导致模型失真。
setMu(double mu):设置最大边长因子。该参数定义了最大边长与搜索半径之间的比例关系。较小的mu值会导致生成更多的小三角形,而较大的mu值会生成较大的三角形。
setMaximumNearestNeighbors(int num):设置最大最近邻点数目。该参数定义了在搜索半径内要考虑的最大最近邻点数目。增大该值可以提高算法的稳定性,但也会增加计算时间。
setMaximumSurfaceAngle(double angle):设置最大表面角度。该参数定义了三角化表面的最大允许角度。较小的角度值会生成更平滑的表面,而较大的角度值会生成更粗糙的表面。
setMinimumAngle(double angle):设置最小角度。该参数定义了三角形的最小允许角度。较小的角度值可以生成更细致的细节,但也可能导致不稳定的三角形。
setMaximumAngle(double angle):设置最大角度。该参数定义了三角形的最大允许角度。较大的角度值可以生成更平坦的表面,但也可能导致模型的失真。
setNormalConsistency(bool consistent):设置法向量一致性。该参数定义了是否要在计算法向量时考虑法向量的一致性。启用法向量一致性可以提高三角化的质量。
2 处理过程可视化


3 代码
#include <pcl/point_types.h>
#include <pcl/io/pcd_io.h>
#include <pcl/search/kdtree.h>
#include <pcl/features/normal_3d.h>
#include <pcl/surface/gp3.h>#include <pcl/visualization/pcl_visualizer.h>int main()
{pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>);pcl::PCLPointCloud2 cloud_blob;pcl::io::loadPCDFile("/home/lrj/work/pointCloudData/bun0.pcd", cloud_blob);pcl::fromPCLPointCloud2(cloud_blob, *cloud);// Normal estimation*pcl::NormalEstimation<pcl::PointXYZ, pcl::Normal> ne;pcl::search::KdTree<pcl::PointXYZ>::Ptr tree(new pcl::search::KdTree<pcl::PointXYZ>);tree->setInputCloud(cloud);ne.setInputCloud(cloud);ne.setSearchMethod(tree);ne.setKSearch(20);pcl::PointCloud<pcl::Normal>::Ptr normals(new pcl::PointCloud<pcl::Normal>);ne.compute(*normals);//* normals contain the point normals + surface curvaturespcl::PointCloud<pcl::PointNormal>::Ptr cloud_with_normals(new pcl::PointCloud<pcl::PointNormal>);pcl::concatenateFields(*cloud, *normals, *cloud_with_normals);pcl::search::KdTree<pcl::PointNormal>::Ptr tree2(new pcl::search::KdTree<pcl::PointNormal>);tree2->setInputCloud(cloud_with_normals);pcl::GreedyProjectionTriangulation<pcl::PointNormal> gp3;pcl::PolygonMesh triangles;gp3.setSearchRadius(0.1);gp3.setMu(2.5);gp3.setMaximumNearestNeighbors(100);gp3.setMaximumSurfaceAngle(M_PI*1.5);gp3.setMinimumAngle(M_PI/180);gp3.setMaximumAngle(2*M_PI/3);gp3.setNormalConsistency(false);gp3.setInputCloud(cloud_with_normals);gp3.setSearchMethod(tree2);gp3.reconstruct(triangles);std::vector<int> parts = gp3.getPartIDs();std::vector<int> states = gp3.getPointStates();pcl::visualization::PCLVisualizer vis("cloud visualization");vis.addCoordinateSystem(0.1);vis.addPolygonMesh(triangles);while(!vis.wasStopped()){vis.spinOnce();}}
相关文章:

【点云surface】无序点云快速三角化
1 介绍 GreedyProjectionTriangulation 是一种基于局部二维投影的三维点贪婪三角剖分算法的实现。它假定局部表面光滑,不同点密度区域之间的过渡相对平滑。 GreedyProjectionTriangulation算法的基本思想是通过逐步投影点云数据到一个三角化网格上来进行重建。它首…...

el-select多选下拉框实现全选功能
<el-selectv-model"query.web_ids"multiplecollapse-tagscollapse-tags-tooltip:max-collapse-tags"2"filterableplaceholder"网站"><li class"checkAllBox" style"padding: 0 32px 0 20px; border-bottom: 1px solid #…...
详解)
Elasticsearch 聚合查询(Aggregation)详解
Elasticsearch中的聚合查询,类似SQL的SUM/AVG/COUNT/GROUP BY分组查询,主要用于统计分析场景。 实例: import org.apache.http.HttpHost; import org.elasticsearch.action.search.SearchRequest; import org.elasticsearch.action.search.…...
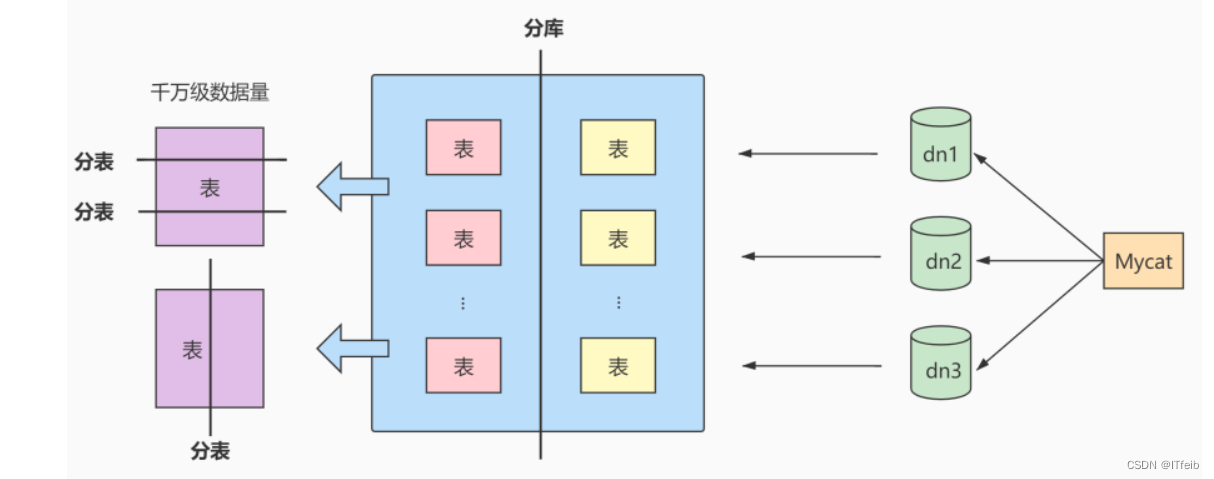
数据库其它调优策略
文章目录 1. 优化MySQL服务器2. 优化数据库结构2.1 差分表:冷热数据分离 3. 大表优化3.1 读/写分离3.2 垂直拆分3.3 水平拆分 1. 优化MySQL服务器 电商平台,双十一,CPU使用率达到99%,系统的计算资源已经耗尽,再也无法…...

【AI认证笔记】NO.2人工智能的发展
目录 一、人工智能的发展里程碑 二、当前人工智能的发展特点 1.人工智能进入高速发展阶段 2.人工智能元年 三、人工智能高速发展的三大引擎 1.算法突破 2.算力飞跃 3.数据井喷 四、AI的机遇 五、AI人才的缺口 六、行业AI 人工智能算法,万物互联ÿ…...

Python与设计模式--观察者模式
23种计模式之 前言 (5)单例模式、工厂模式、简单工厂模式、抽象工厂模式、建造者模式、原型模式、(7)代理模式、装饰器模式、适配器模式、门面模式、组合模式、享元模式、桥梁模式、(11)策略模式、责任链模式、命令模式、中介者模…...
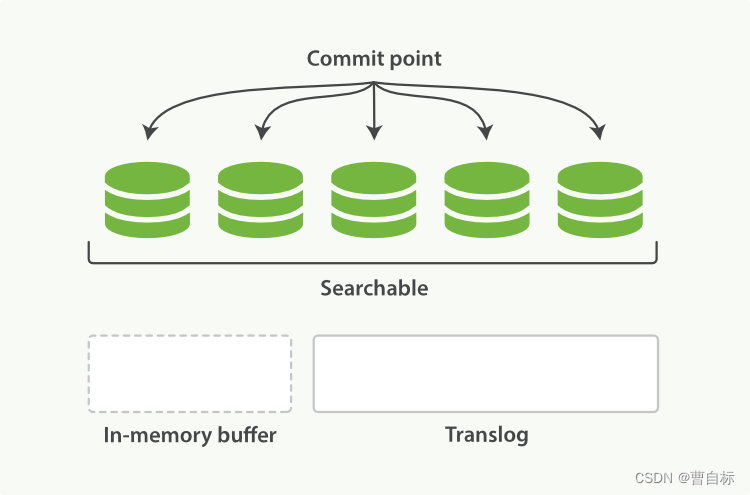
Elasticsearch底层原理分析——新建、索引文档
es版本 8.1.0 重要概念回顾 Elasticsearch Node的角色 与下文流程相关的角色介绍: Node Roles配置主要功能说明masternode.roles: [ master ]有资格参与选举成为master节点,从而进行集群范围的管理工作,如创建或删除索引、跟踪哪些节点是…...

ts实现合并数组对象中key相同的数据
背景 在平常的业务中,后端同学会返回以下类似的结构数据 // 后端返回的数据结构 [{ id: 1, product_id: 1, pid_name: "Asia", name: "HKG01" },{ id: 2, product_id: 1, pid_name: "Asia", name: "SH01" },{ id: 3, pro…...
C语言--根据成绩判断等级
一.题目描述 如果学生的成绩小于60分,那么输出不及格 如果学生的成绩大于60分小于85分,那么输出良好 如果学生的成绩大于85分,那么输出优秀 二.代码实现 #define _CRT_SECURE_NO_WARNINGS #include<stdio.h> //根据成绩打印等级 //scor…...

Rust多线程任务,发现有些线程一直获取不到锁【已解决】
问题描述 项目中用到rust,其中在多线程中用到了同一个对象的锁,然而发现其中一个线程一直拿不到这个锁。 解决过程 我先是在线程A中加入了sleep方法,这样做的效果就是,比最初好一些,但是拿到锁还是要较长时间…...

【区块链】产品经理的NFT初探
常见的FT如比特币(BTC),以太币(ETH)等,两个代币之间是完全可替换的。而NFT具有唯一性,不可以互相替换。本文作者对NET的发展现状、相关协议、应用场景等方面进行了分析,一起来看一下…...

香港服务器减少延迟的几种方法
我们在租用香港服务器时,总觉得网站程序反应太慢。选择了香港服务器的开发商和企业对香港服务器目前的访问速度不满意 怎么办?第一点是换服务器。更换配置更大、带宽更高的服务器,可以更好的解决网站访问速度。如何减少香港服务器的延时 速度…...

PowerShell命令小记
1. 使用命令删除指定文件或文件夹 在 PowerShell 中,你可以使用 Remove-Item 命令递归删除文件夹下的指定文件。以下是一条命令的示例,该命令删除指定文件夹及其子文件夹中的所有 .txt 文件: Remove-Item -Path "D:\test" -Recur…...

C语言小练
目录 打印斐波那契数列指定位置的值 给定两个数,求这两个数的最大公约数 三个数从大到小输出 模拟用户登陆情况,且只能输如三次 采用二分法查找数组中的指定元素 打印输出九九乘法表 数一下1-100中所有整数出现多少个数字9 打印1-200之间的素数&…...
Webhook端口中的自签名身份验证
概述 有时,可能需要通过 Webhook 端口从交易伙伴处接收数据,但该交易伙伴可能需要更多的安全性,而不仅仅是用于验证入站 Webhook 请求的基本身份验证用户名/密码 – 或者您可能只想在入站 Webhook 消息上添加额外的安全层。 使用 Webhook 端…...
:变量、嵌套规则和混合器等高级功能)
CSS预处理器(如Sass或Less):变量、嵌套规则和混合器等高级功能
在Vue项目中,可以使用CSS预处理器(如Sass或Less)来编写样式。 这些预处理器提供了一些高级功能,如变量、嵌套规则和混合器等。 1. 变量 在Sass中,我们可以使用$符号定义变量。这些变量方便我们在多个地方重复使用&a…...

【Linux】Linux第一个小程序 --- 进度条
👦个人主页:Weraphael ✍🏻作者简介:目前正在学习c和Linux还有算法 ✈️专栏:Linux 🐋 希望大家多多支持,咱一起进步!😁 如果文章有啥瑕疵,希望大佬指点一二 …...

每日一练:约瑟夫生者死者小游戏
1. 问题描述 约瑟夫问题(Josephus problem)是一个经典的数学和计算机科学问题,源于犹太历史学家弗拉维奥约瑟夫斯(Flavius Josephus)的著作《犹太战记》。问题的描述如下: 在这个问题中,有n…...

双指针算法(题目与答案讲解)
文章目录 题目移动零复写零两数之和N数之和(>2个数) 答案讲解移动零复写零两数之和N数之和 题目 力扣 移动零 1、移动零:题目链接 复写零 2、复写零:题目链接 两数之和 3、两数之和题目链接 N数之和(>2个数) 4、N数之和(三个数、四个数) 三个数:题目链接 四个数题目链接…...
python服装电商系统vue购物商城django-pycharm毕业设计项目推荐
系统面向的使用群体为商家和消费者,商家和消费者所承担的功能各不相同,所对象的权限也各不相同。对于消费者和商家设计的功能如下: 对于消费者设计了五大功能模块: (1) 商品信息:用户可在商品…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...
