SIFI 极值点拟合的详细推导过程
在获得高斯差分金字塔之后,我们可以根据邻近尺度和邻近像素一共 26 个像素点的灰度值和中心像素点的灰度值比较,如果中心像素点的值是最大或者最小的,则作为极值点保留下来。
但是我们知道像素是网格排布的,也就是说是离散的,如果我们想要获得更精确的极值点,就需要根据目前离散的点进行插值拟合,让数据连续起来,然后得到一个比较精确的极值点。
给我的感觉就是 SIFT 算法经历了一个从连续到离散,然后再回归连续的过程,首先是通过离散的高斯差分来近似表示拉普拉斯梯度,减少计算量,然后又对离散的高斯差分进行子像元级别的插值,获得一个连续的曲面,求真正的极值点。
首先,我们的高斯差分函数是通过通过不同尺度的高斯滤波得到的: D ( x , y , σ ) = [ G ( x , y , σ 1 ) − G ( x , y , σ 2 ) ] ∗ I ( x , y ) D(x, y, \sigma) = [G(x, y, \sigma_1 ) - G(x, y, \sigma_2 )] * I(x,y) D(x,y,σ)=[G(x,y,σ1)−G(x,y,σ2)]∗I(x,y)其中, I ( x , y ) I(x, y) I(x,y) 是像素的灰度值。
然后在尺度 σ \sigma σ 下,我们要从离散的高斯差分插值到连续的曲面,需要用到泰勒展开,因为泰勒展开是一种将函数在某一点附近近似为多项式的方法,通过使用一阶和二阶导数来拟合函数。所以可以得到: D ( X ) ≈ D + ∂ D T ∂ X X + 1 2 X T ∂ 2 D ∂ X 2 X D(X) \approx D +\frac{ \partial D^T }{\partial X } X + \frac{1}{2}X^T\frac{\partial^2 D}{\partial X^2}X D(X)≈D+∂X∂DTX+21XT∂X2∂2DX这个公式在别的文章很常见,但是我觉得不够直观,因为是尺度已经确定了是 σ \sigma σ 所以高斯差分函数目前是关于位置 x , y x, y x,y 的函数,上面的式子是一个矩阵的形式,因为要求极值,所以要对 D ( X ) D(X) D(X) 求导,并让其导数 ∂ D ∂ X = 0 \frac{\partial D}{\partial X} = 0 ∂X∂D=0 : ∂ D ∂ X = 0 + ∂ D T ∂ X + 1 2 ( ∂ 2 D ∂ X 2 + ( ∂ 2 D ∂ X 2 ) T ) X \frac{\partial D}{\partial X} = 0 + \frac{\partial D^T}{\partial X}+ \frac{1}{2}\left(\frac{\partial^2 D}{\partial X^2}+\left(\frac{\partial^2 D}{\partial X^2}\right)^T \right)X ∂X∂D=0+∂X∂DT+21(∂X2∂2D+(∂X2∂2D)T)X考虑到 ∂ 2 D ∂ X 2 \frac{\partial^2 D}{\partial X^2} ∂X2∂2D 是 Hessian 矩阵,展开表达式如下: ∂ 2 D ∂ X 2 = ( ∂ 2 D ∂ x 2 ∂ 2 D ∂ x ∂ y ∂ 2 D ∂ x ∂ y ∂ 2 D ∂ y 2 ) \frac{\partial^2 D}{\partial X^2} = \begin{pmatrix} \frac{\partial ^2D}{\partial x^2} & \frac{\partial ^2D}{\partial x\partial y}\\ \frac{\partial ^2D}{\partial x\partial y} & \frac{\partial ^2D}{\partial y^2} \end{pmatrix} ∂X2∂2D=(∂x2∂2D∂x∂y∂2D∂x∂y∂2D∂y2∂2D)可以看出来是对称矩阵,所以 ∂ 2 D ∂ X 2 = ( ∂ 2 D ∂ X 2 ) T \frac{\partial^2 D}{\partial X^2} = (\frac{\partial^2 D}{\partial X^2})^T ∂X2∂2D=(∂X2∂2D)T,我们就可以得到求导之后的式子为: ∂ D ∂ X = ∂ D T ∂ X + ∂ 2 D ∂ X 2 X \frac{\partial D}{\partial X} = \frac{\partial D^T}{\partial X}+ \frac{\partial^2 D}{\partial X^2}X ∂X∂D=∂X∂DT+∂X2∂2DX让导数 ∂ D ∂ X \frac{\partial D}{\partial X} ∂X∂D 为零可以得到: X ^ = ∂ D T ∂ X ( − ∂ 2 D ∂ X 2 ) − 1 \hat{X} = \frac{\partial D^T}{\partial X} \left (- \frac{\partial^2 D}{\partial X^2} \right )^{-1} X^=∂X∂DT(−∂X2∂2D)−1这里的 X ^ \hat{X} X^ 就是我们要求的极值点偏移值,然后将其代入原式,就可以求得极值点的响应值: D ( X ) = D + 1 2 ∂ D T ∂ X X ^ D(X) = D + \frac{1}{2} \frac{\partial D^T}{\partial X} \hat{X} D(X)=D+21∂X∂DTX^
∂ ∂ X ( X T A X ) = ( A + A T ) X \frac{\partial }{\partial X}(X^T A X) = (A+A^T)X ∂X∂(XTAX)=(A+AT)X
相关文章:

SIFI 极值点拟合的详细推导过程
在获得高斯差分金字塔之后,我们可以根据邻近尺度和邻近像素一共 26 个像素点的灰度值和中心像素点的灰度值比较,如果中心像素点的值是最大或者最小的,则作为极值点保留下来。 但是我们知道像素是网格排布的,也就是说是离散的&…...
Kontakt v7.7.2(音频采样器)
Native Instruments Kontakt 7是一款强大的软件采样器,它允许用户从各种来源采样音频并进行编辑和处理。它包含大量预设采样库,包括乐器、合成器、鼓组和声音效果等。此外,Kontakt 7还允许用户创建自己的采样库,以便根据自己的需要…...
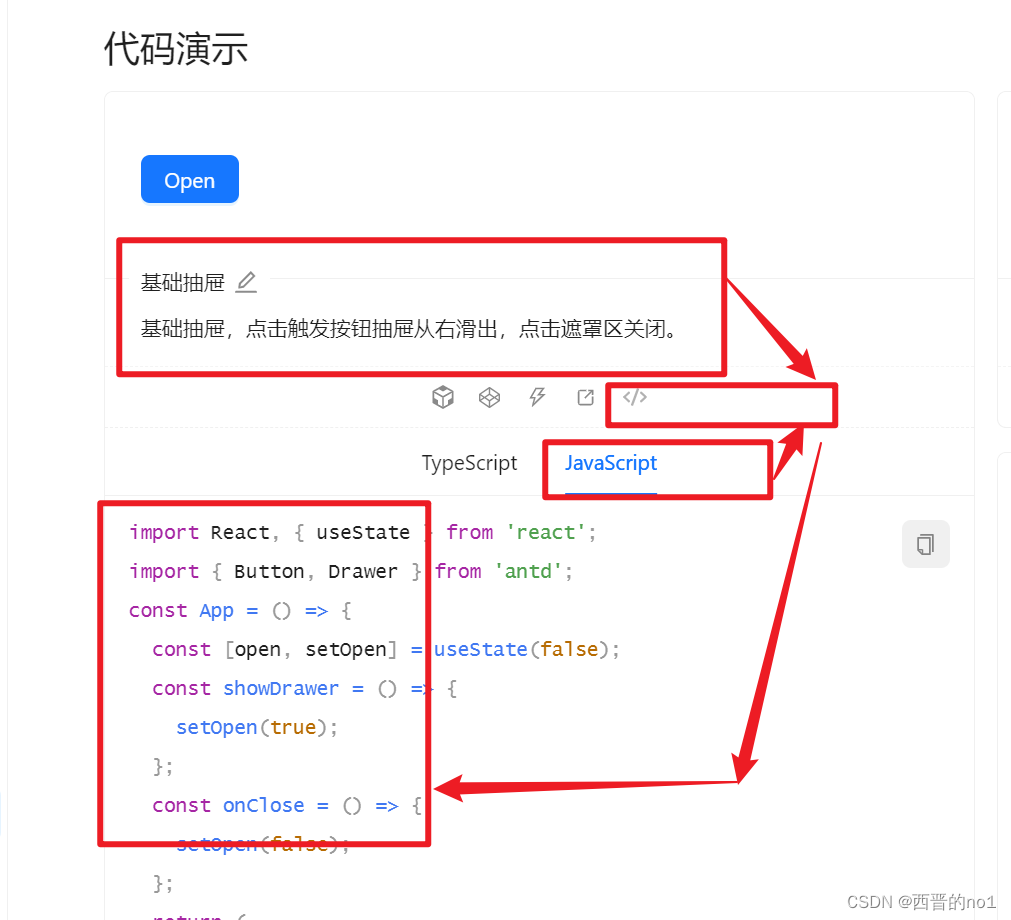
Drawer抽屉(antd-design组件库)简单用法
1.Drawer抽屉 屏幕边缘滑出的浮层面板。 2.何时使用 抽屉从父窗体边缘滑入,覆盖住部分父窗体内容。用户在抽屉内操作时不必离开当前任务,操作完成后,可以平滑地回到原任务。 需要一个附加的面板来控制父窗体内容,这个面板在需要时…...

Android控件全解手册 - 多语言切换完美解决方案(兼容7.0以上版本)
Unity3D特效百例案例项目实战源码Android-Unity实战问题汇总游戏脚本-辅助自动化Android控件全解手册再战Android系列Scratch编程案例软考全系列Unity3D学习专栏蓝桥系列ChatGPT和AIGC 👉关于作者 专注于Android/Unity和各种游戏开发技巧,以及各种资源分…...
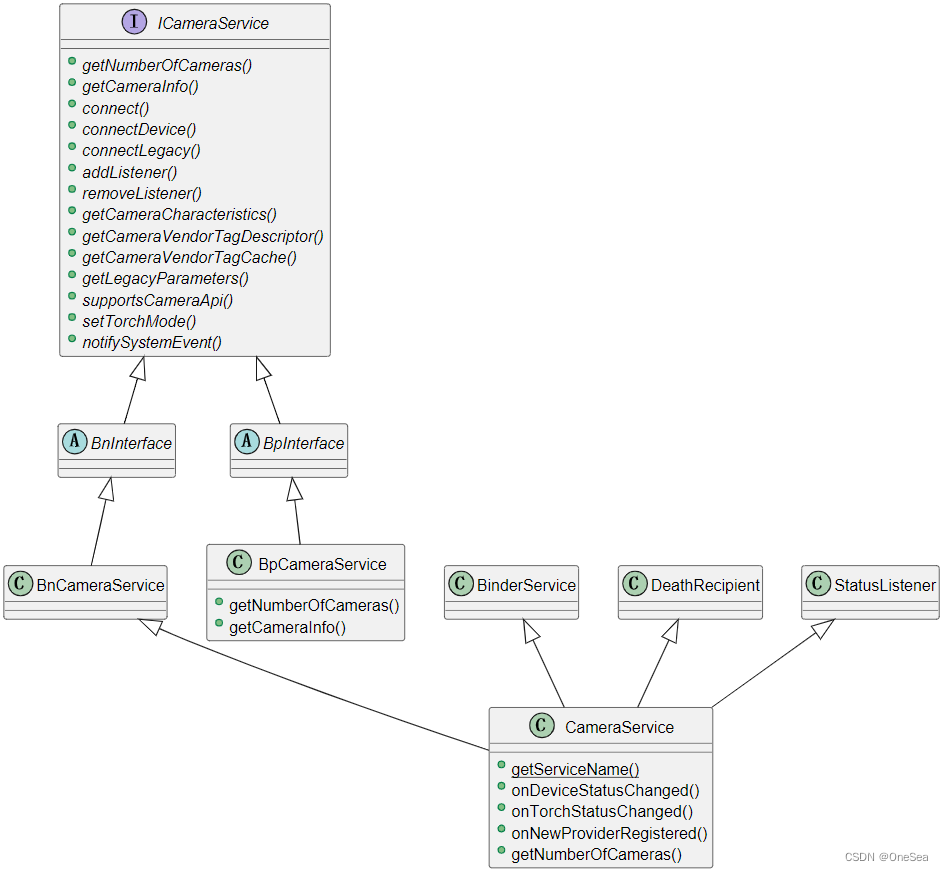
Android-P CameraSerivce
0 前言 本文重点分析Android-P的CameraService实现。 验证:Goldfish模拟器 1 定义 图1.1 CameraService ICameraServiceframeworks/av/camera/aidl/android/hardware/ICameraService.aidlBnCameraServiceout/soong/.intermediates/frameworks/av/camera/libcamera_client/an…...
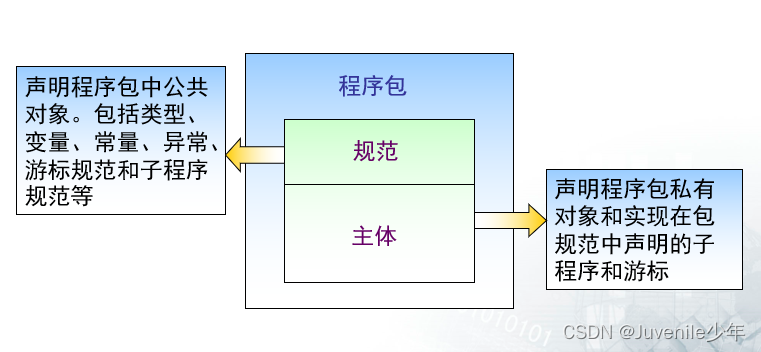
21.Oracle的程序包(Package)
Oracle的程序包Package 一、Package的概述1、什么是Oracle11g的Package2、Package的作用是什么3、常见的系统内置Package 二、创建Package的相关语法1、Package的创建语法2、Package的删除3、具体案例4、Package的使用5、与Package相关的其他语法 三、常见内置程序包的使用1、…...

Spring 日志
日志的作用: 1.定位和发现问题 2.系统监控 3.数据采集 观察日志 先写一段打印日志的代码 日志内容 日志级别分类 默认日志级别是Info,级别一下的就不打印了 Spring 帮我们集成了日志框架,我们直接使用即可 我们测试一下用日志框架打印日志是如何 我们就会发现打印的结果跟…...
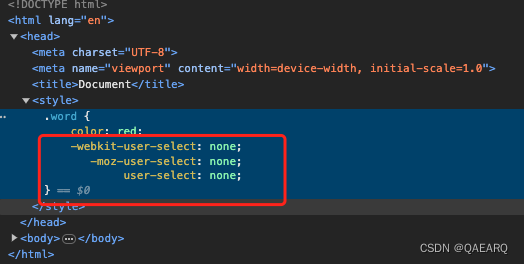
webpack如何处理浏览器的样式兼容问题postcss
一、准备工作 css/index.css添加样式 .word {color: red;user-select: none; } 为了兼容不同的浏览器我们需要添加前缀比如: -webkit-user-select: none; 这个工作可以通过postcss的插件postcss-preset-env处理 二、安装依赖 pnpm i -D postcss postcss-loader…...
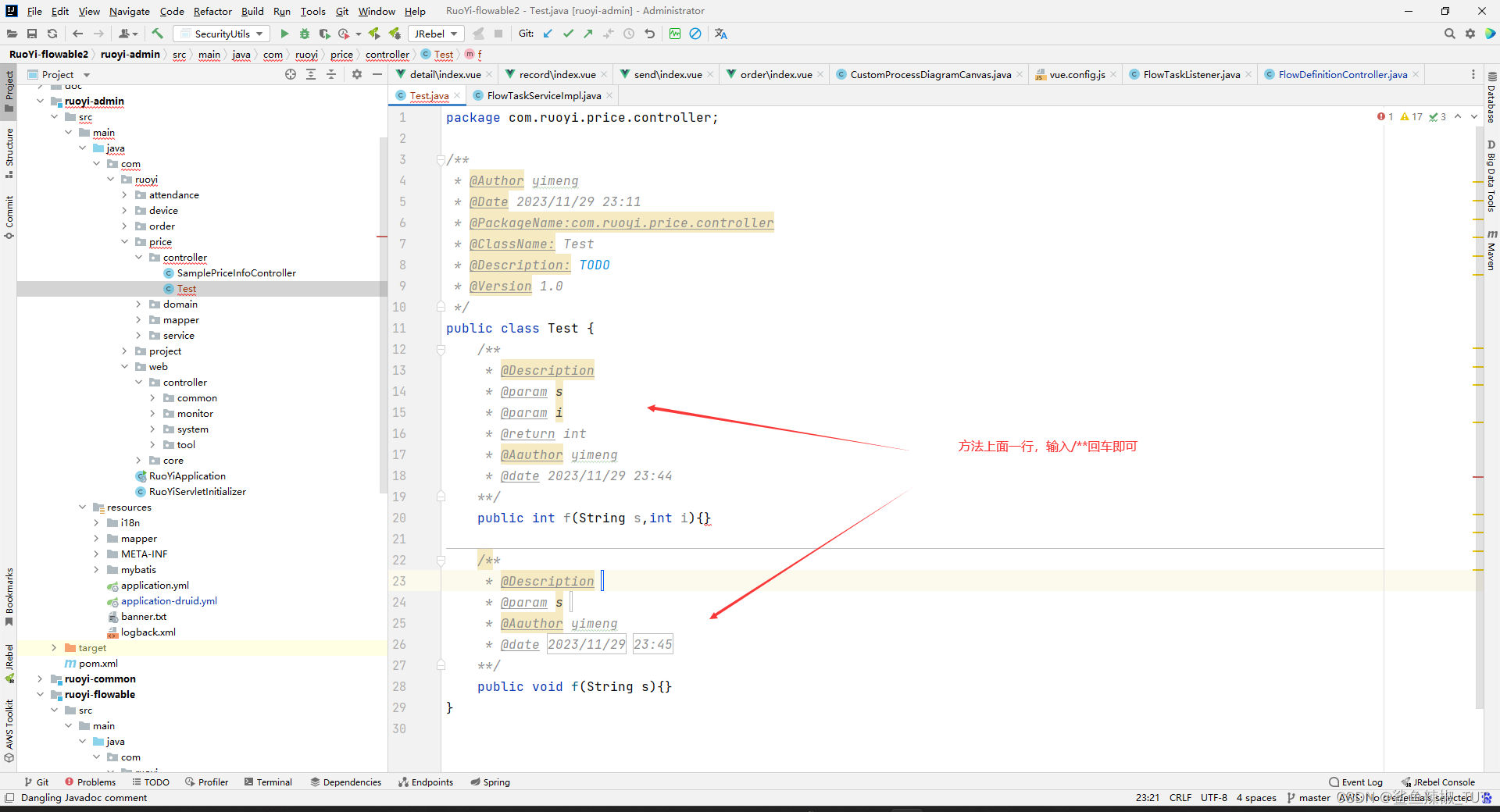
idea方法注释模版设置
方法上面的注释模版: Template text: ** Description $desc$ $param$ $return$* Aauthor yimeng* date $DATE$ $TIME$ **/param: groovyScript("def result ;def params \"${_1}\".replaceAll([\\\\[|\\\\]|\\\\s], ).split(,).toLis…...

NX二次开发UF_CURVE_create_isocline 函数介绍
文章作者:里海 来源网站:https://blog.csdn.net/WangPaiFeiXingYuan UF_CURVE_create_isocline Defined in: uf_curve.h int UF_CURVE_create_isocline(int face_cnt, tag_t faces [ ] , double direction [ 3 ] , const char * start_angle, const ch…...

从0开始学习JavaScript--JavaScript 模板字符串的全面应用
JavaScript 模板字符串是 ES6 引入的一项强大特性,它提供了一种更优雅、更灵活的字符串拼接方式。在本文中,将深入探讨模板字符串的基本语法、高级用法以及在实际项目中的广泛应用,通过丰富的示例代码带你领略模板字符串的魅力。 模板字符串…...

开源 vs 闭源:数字化时代的技术选择
开源 vs 闭源:数字化时代的技术选择 近期,特斯拉CEO马斯克的一番言论引起了广泛关注:OpenAI不该闭源,自家首款聊天机器人将开源。这引发了人们对于开源与闭源软件的辩论,这一话题在技术界一直是热门的讨论焦点。在数字…...

Spring Boot项目Service类单元测试自动生成
在Spring Boot项目中,对Service类进行单元测试对于开发工程师而言具有重大意义和作用: 验证业务逻辑的正确性和完整性 核心业务逻辑的准确实现:Service类通常包含核心业务逻辑。单元测试确保这些逻辑被正确实现,满足业务需求。处…...

Typescript中 interface 和 type 的区别是什么?
在 TypeScript 中,interface 和 type 都用于定义类型,但它们有一些区别。 1. 语法差异: interface 关键字用于声明接口,使用 interface 可以定义对象的形状、函数的签名等。 type 关键字用于声明类型别名,可以给一个…...

W2311294-万宾科技可燃气体监测仪怎么进行数据监测
万宾科技可燃气体监测仪怎么进行数据监测 燃气是现代城市之中重要的能源,它已经渗透到城市生活的方方面面,对燃气管网的管理也在考验着政府人员的工作能力。燃气管网的安全运行和城市的安全和人民的生活直接挂钩。为了及时掌握燃气管网的运行状态&#x…...
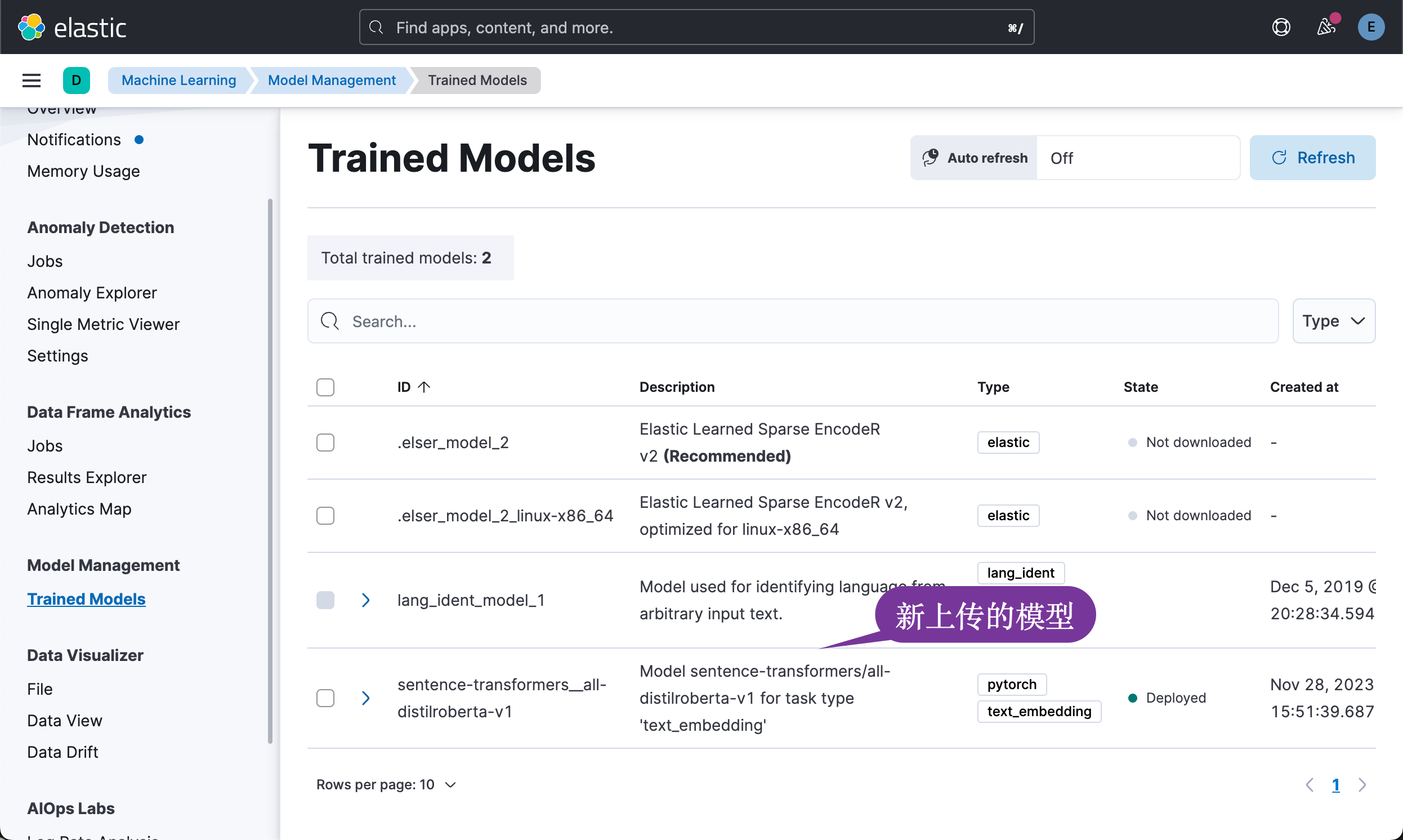
Elasticsearch:向量搜索 (kNN) 实施指南 - API 版
作者:Jeff Vestal 本指南重点介绍通过 HTTP 或 Python 使用 Elasticsearch API 设置 Elasticsearch 以进行近似 k 最近邻 (kNN) 搜索。 对于主要使用 Kibana 或希望通过 UI 进行测试的用户,请访问使用 Elastic 爬虫的语义搜索入门指南。你也可以参考文章…...

704 二分查找 day1
class Solution { public: int search(vector<int>& nums, int target) { int left 0; int right nums.size() - 1; // 定义target在左闭右闭的区间里,[left, right] while (left < right) { // 当leftright,区间[left, right]依然有效&…...

Python面试破解:return和yield的细腻差别
更多Python学习内容:ipengtao.com 大家好,我是涛哥,今天为大家分享 Python面试破解:return和yield的细腻差别,全文3000字,阅读大约10钟。 在Python的函数编程中,return和yield是两个常用的关键词…...
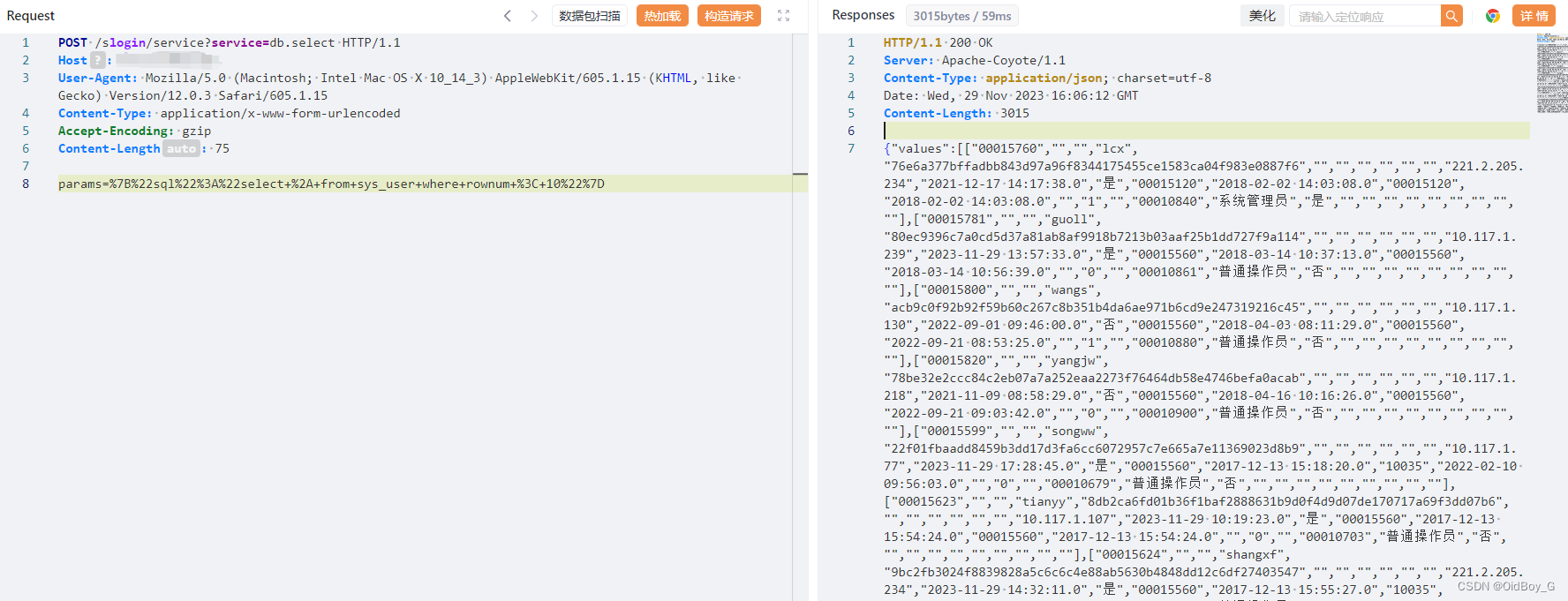
云时空社会化商业 ERP 系统 service SQL 注入漏洞复现
0x01 产品简介 时空云社会化商业ERP(简称时空云ERP) ,该产品采用JAVA语言和Oracle数据库, 融合用友软件的先进管理理念,汇集各医药企业特色管理需求,通过规范各个流通环节从而提高企业竞争力、降低人员成本…...
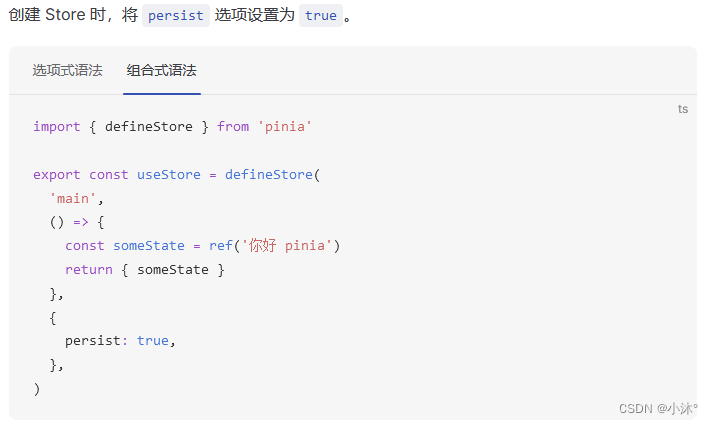
Vue3-Pinia
Pinia是什么 Pinia是Vue的最新状态管理工具,是Vuex的替代品 比Vuex更大的优势在于: 1.提供更加简单的API(去掉了mutation) 2.提供符合,组合式风格的API(和Vue3新语法统一) 3.去掉了modules…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...
