数据类型及强制转换
数据类型范围(基本)
| 数据类型 | 占内存字节数 | 表示范围 | 数量级 |
|---|---|---|---|
| char(signed char) | 1 | -128~127 | 2 |
| unsigned char | 1 | 0~255 | 2 |
| short int(signed short int) | 2 | -32,768~32,767 | 4 |
| unsigned short int | 2 | 0~65,535 | 4 |
| int(signed int) | 4 | -2,147,483,648~2,147,483,647(-231 ~ 231-1) | 9 |
| unsigned int | 4 | 0~4,294,967,295 | 9 |
| long int(signed long int) | 4 | -2,147,483,648~2,147,483,647(-231 ~ 231-1) | 9 |
| unsigned long int | 4 | 0~4,294,967,295 | 9 |
| float | 4 | -3.4x10-38 ~ 3.4x1038 | 38 |
| double | 8 | -1.7x10-308 ~ 1.7x10308 | 308 |
| long double | 8 | -1.7x10-308 ~ 1.7x10308 | 308 |
有符号与无符号数据
- 无符号数据(Unsigned Data):无符号数据只能表示非负整数。在内存中,无符号数据占用固定大小的存储空间,如8位、16位、32位等,视具体类型而定。例如,8位无符号数据可以表示0到255之间的整数。如果一个数值超出了该范围,那么它将会被截断或者溢出。在编程语言如C++中,通常使用“unsigned”关键字来表示无符号数据类型。
- 有符号数据(Signed Data):有符号数据可以表示正数、负数和零。在内存中,有符号数据同样占用固定大小的存储空间,但是可以表示的范围比无符号数据更大。例如,8位有符号数据可以表示-128到127之间的整数。这是因为存储空间的一部分被用来表示负数,所以正数的表示范围相应地减少了。在编程语言如C++中,通常使用默认的整数类型来表示有符号数据。
无符号16位强制转换为有符号
python
# 强制转换为16位有符号数据
def get_s16(val):if val < 0x8000: # 32768return valelse:return (val - 0x10000) # val - 65536
参考文章:
C语言基本数据类型及其范围
Python中读取到16进制数如何转成有符号数值
相关文章:

数据类型及强制转换
数据类型范围(基本) 数据类型占内存字节数表示范围数量级char(signed char)1-128~1272unsigned char10~2552short int(signed short int)2-32,768~32,7674unsigned short int20~65,5354int(sig…...

Python----高阶函数
高阶函数:把函数作为参数传入,这样的函数称为高阶函数,高阶函数是函数式编程的体现。函数式编程就是指这种高度抽象的编程范式。 高阶函数的由来 在Python中,abs()函数可以完成对数字求绝对值计算。 ① 正数的绝对值是它本身 ②…...

Unity地面交互效果——6、地形动态顶点置换和曲面细分
回到目录 Unity置换贴图局部距离曲面细分 大家好,我是阿赵。 这篇文章是我无聊的时候做了一个demo,觉得挺有趣,于是就发上来。这里面包含了4个内容:置换贴图、顶点偏移、局部曲面细分,曲面细分按距离调整强度。 …...
)
Linux系统服务之一次性服务(2)
接前一篇文章:Linux系统服务之一次性服务(1) 本文内容参考以下文章: Systemd OneShot 系统启动时运行一次特定的命令或脚本,并在执行完毕后自动退出-CSDN博客 oneshot一次性服务_typeoneshot-CSDN博客 systemd.serv…...
Vue项目解决van-calendar 显示白色空白,需滑动一下屏幕,才可正常显示
问题描述,如图 ipad(平板)或者 H5移动端引入Vant组件的日历组件(van-calendar),初始化显示空白,需滚动一下屏幕,才可正常显示 解决方法 需在van-calendar上绑定open"openCalendar"事件…...
Linux:可视化管理工具Webmin的安装
一、下载 地址:Webmin官网 我这里下载的是1.700-1版本 二、安装 1、在虚拟机上新建目录并安装软件 mkdir /opt/webmin rpm -ivh webmin-1.700-1.noarch.rpm2、修改webmin的root密码 /usr/libexec/webmin/changepass.pl /etc/webmin root 1234563、修改端口(可…...
WARNING: Access control is not enabled for the database.
MongoDB shell version v3.4.24 WARNING: Access control is not enabled for the database. Read and write access to data and configuration is unrestricted. 1)未启用访问控制 2)读写访问不受限制 D:\MongoDB\Server\3.4\bin>mongo MongoDB shell version v3.4.24 c…...
JavaScript编程进阶 – Return语句
JavaScript编程进阶 – Return语句 JavaScript Programming Advanced – Return Statement By JacksonML 就像人们习惯的函数一样,总觉得在函数体最后需要一个return语句,标志着函数的结束,就像下面这个函数 theFunc() 那样。 function theFunc() { re…...

Python与设计模式--备忘录模式
23种计模式之 前言 (5)单例模式、工厂模式、简单工厂模式、抽象工厂模式、建造者模式、原型模式、(7)代理模式、装饰器模式、适配器模式、门面模式、组合模式、享元模式、桥梁模式、(11)策略模式、责任链模式、命令模式、中介者模…...

04_Flutter自定义Slider滑块
04_Flutter自定义Slider滑块 一.Slider控件基本用法 Column(mainAxisAlignment: MainAxisAlignment.start,children: <Widget>[Text("sliderValue: ${_sliderValue.toInt()}"),Slider(value: _sliderValue,min: 0,max: 100,divisions: 10,thumbColor: Colors.…...

服务器数据恢复—EMC存储raid5故障导致上层应用崩溃的数据恢复案例
服务器存储数据恢复环境: EMC某型号存储,8块组建一组raid5磁盘阵列。上层操作系统采用zfs文件系统。 服务器存储故障&分析: raid5阵列中有2块硬盘未知原因离线,raid5阵列崩溃,上层应用无法正常使用。 服务器数据恢…...
7.1 Windows驱动开发:内核监控进程与线程回调
在前面的文章中LyShark一直在重复的实现对系统底层模块的枚举,今天我们将展开一个新的话题,内核监控,我们以监控进程线程创建为例,在Win10系统中监控进程与线程可以使用微软提供给我们的两个新函数来实现,此类函数的原…...
基于ssm的汽车论坛管理系统设计与实现
基于ssm的汽车论坛管理系统设计与实现 摘要:信息化社会内需要与之针对性的信息获取途径,但是途径的扩展基本上为人们所努力的方向,由于站在的角度存在偏差,人们经常能够获得不同类型信息,这也是技术最为难以攻克的课题…...
)
实习开发日志经验总结(一)
文章目录 前言实习日志经验总结 前言 自己之前实习过程中遇到的问题以及相应的解决过程,我都有记录形成比较凌乱的实习日志。故想在整个实习日志的基础上,提炼一些技术知识点或者是解决问题的思路。考虑到实习项目的不方便公开性,所以会隐去…...

【Unity基础】8.简单场景的搭建
【Unity基础】8.简单场景的搭建 大家好,我是Lampard~~ 欢迎来到Unity基础系列博客,所学知识来自B站阿发老师~感谢 (一)场景资源 (1)Import资源包 今天我们将手动去搭一个简单的场景,当…...
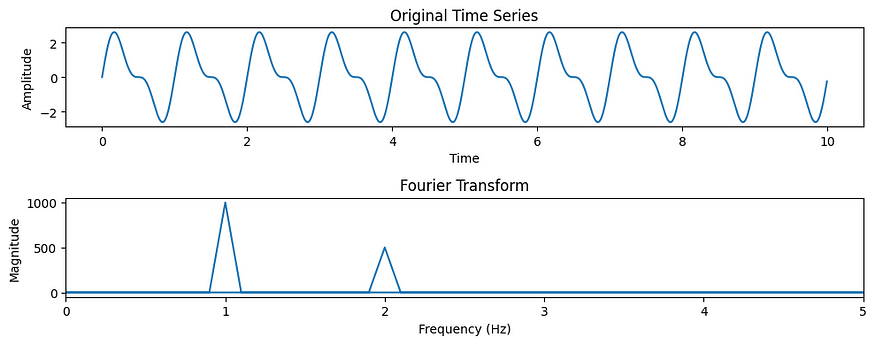
傅里叶变换及其在机器学习中的应用
一、介绍 傅立叶变换是一种数学技术,在各个科学和工程领域发挥着关键作用,其应用范围从信号处理到量子力学。近年来,它在机器学习领域发现了新的意义。本文探讨了傅里叶变换的基础知识及其在机器学习应用中日益增长的重要性。 …...

xorm源码学习
文章目录 XORM源码浅析及实践ORMORM vs. SQLXORM软件架构 ORM 引擎 Engine——DBM*core.DB Golang:database/sql 源码基本结构连接复用,提高性能。增加数据库连接池数量连接管理 database/sql主要内容:sql.DB创建数据库连接sql.Open()DB.conn…...

Vue3中的<script setup>和<script>的区别
相同点 在一个 Vue3 单文件组件 (SFC)中,<script setup> 和 <script> 它们各自最多只能存在一个。 不同点 <script setup> 这个脚本块将被预处理为组件的 setup() 函数,这意味着它将为每一个(也可以说每一次)组件实例都执行。 <…...
)
Docker笔记-Docker搭建最新版zabbix服务端(2023-07-31)
前言 一开始问chartgpt上,搭建的思路是对的,但命令和细节有问题,最后还是依靠StackOverflow解决的。一开始在amd的linux上搭建好docker版的zabbix,但放到arm的机器上就报错了,原因是指令集不匹配,最后跑到…...

QT配合CSS隐藏按钮
第一种方法 在Qt的CSS样式表中,使用 visibility 属性来隐藏按钮。设置 visibility 为 hidden 不可见,而设置为 visible 则可见。 隐藏所有 QPushButton QPushButton {visibility: hidden; }隐藏特定的按钮,用按钮的名称或样式类进行定位就…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

解决:Android studio 编译后报错\app\src\main\cpp\CMakeLists.txt‘ to exist
现象: android studio报错: [CXX1409] D:\GitLab\xxxxx\app.cxx\Debug\3f3w4y1i\arm64-v8a\android_gradle_build.json : expected buildFiles file ‘D:\GitLab\xxxxx\app\src\main\cpp\CMakeLists.txt’ to exist 解决: 不要动CMakeLists.…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...
