傅里叶变换及其在机器学习中的应用
一、介绍
傅立叶变换是一种数学技术,在各个科学和工程领域发挥着关键作用,其应用范围从信号处理到量子力学。近年来,它在机器学习领域发现了新的意义。本文探讨了傅里叶变换的基础知识及其在机器学习应用中日益增长的重要性。
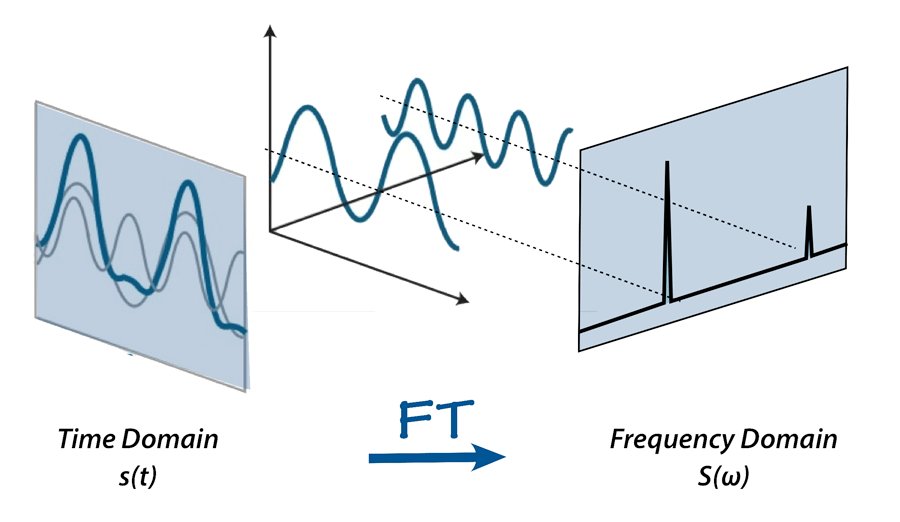
傅里叶变换协调了数据世界,揭示了其中隐藏的交响乐,编排了在整个机器学习领域产生共鸣的见解。
二、理解傅里叶变换
傅里叶变换以法国数学家和物理学家 Jean-Baptiste Joseph Fourier 的名字命名,是一种将信号分解为其组成频率分量的数学运算。它使我们能够分析信号的频率内容并在频域中表示它。这种转换在处理复杂信号时特别有用,因为它简化了对其基础模式的分析。
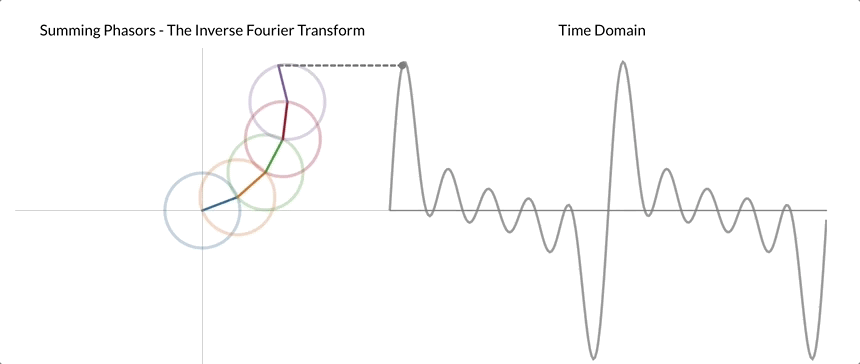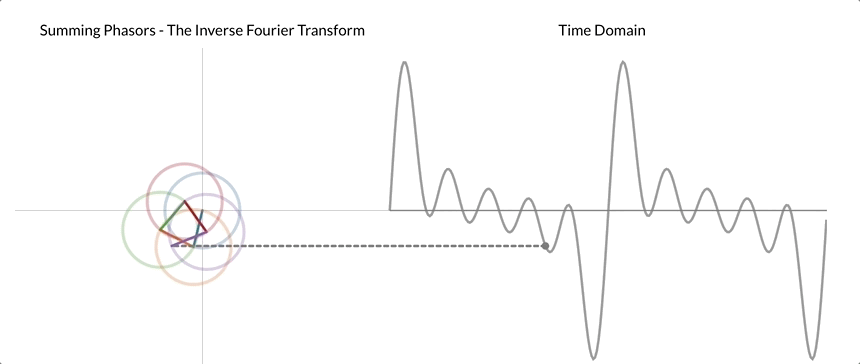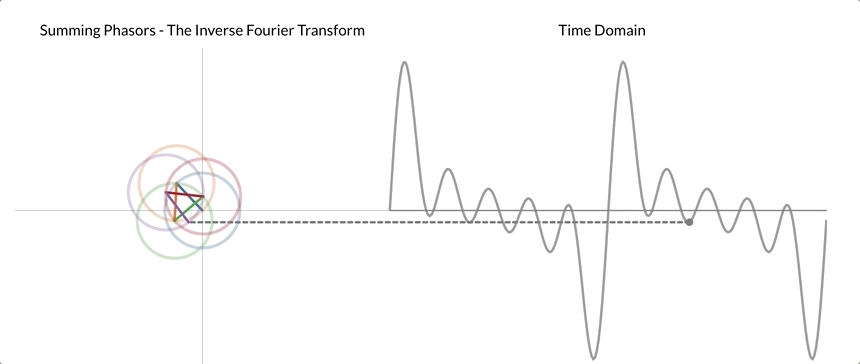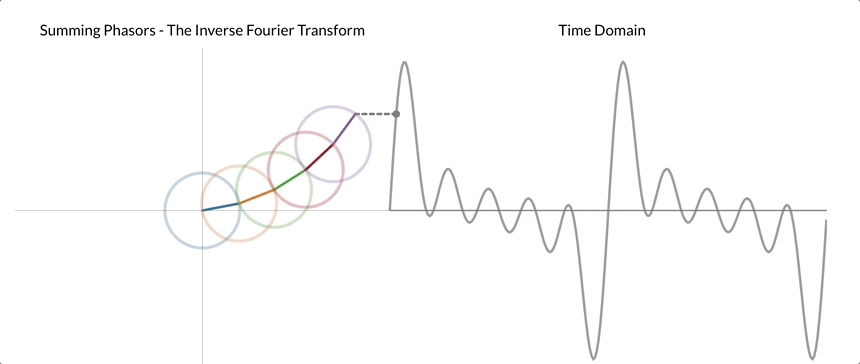
连续傅里叶变换 (CFT) 和离散傅里叶变换 (DFT) 是两种常见的变体。CFT用于连续信号,而DFT应用于离散信号,使其更适合数字数据和机器学习任务。快速傅立叶变换 (FFT) 是计算 DFT 的有效算法,进一步促进了其在各种应用中的广泛使用。
三、信号处理中的应用
傅里叶变换最传统且最成熟的应用之一是信号处理。它用于音频处理、图像分析和数据压缩等任务。例如,在音频处理中,傅立叶变换有助于识别音频信号中存在的各种频率,从而实现语音识别、音乐分类和降噪等任务。
在图像分析中,傅里叶变换可用于从图像中提取纹理和图案信息。通过将图像转换为频域,可以更轻松地检测边缘、形状和其他视觉特征。这对于图像识别、对象检测和图像压缩等任务至关重要。
四、机器学习中的应用
机器学习是一个专注于开发能够从数据中学习的算法的领域,傅里叶变换的使用越来越多。它在这个领域的应用是多样且有影响力的:
- 时间序列分析:在金融、医疗、天气预报等领域,时间序列数据非常丰富。傅立叶变换可以通过分析时间序列数据的频率分量来帮助从时间序列数据中提取相关特征。这对于异常检测、趋势分析和预测等任务至关重要。
- 自然语言处理:当文本数据表示为单词序列时,可以将其视为离散信号。通过应用傅里叶变换,可以在频域中分析文本数据,这在文本分类、情感分析和主题建模中都有应用。
- 特征工程:特征工程是机器学习流程中的关键步骤。通过将数据转换到频域,可以提取在时域中可能难以捕获的有价值的特征。这可以带来更强大、更准确的机器学习模型。
- 卷积神经网络 (CNN): CNN 是一种流行的图像分析深度学习架构。傅里叶变换可用于设计专门检测图像中某些频率分量的卷积滤波器。这可以提高 CNN 在图像分类和对象识别等任务中的性能。
- 数据增强:数据增强是一种用于增加训练数据集大小的技术。在图像处理中,傅里叶变换可用于通过改变图像的频率分量来创建增强数据。这有助于提高机器学习模型的泛化性和鲁棒性。
五、代码
要在 Python 中执行傅里叶变换进行时间序列分析,您可以使用numpy和matplotlib库。我将为您提供一个完整的 Python 代码示例,使用示例数据集并生成相关图。首先,您需要安装必要的库(如果尚未安装):
pip install numpy matplotlib以下是使用傅立叶变换进行时间序列分析的 Python 代码,其中包含示例数据集和绘图:
import numpy as np
import matplotlib.pyplot as plt# Generate a sample time series dataset
# You can replace this with your own time series data
# Ensure that the data is in a NumPy array or a list
time = np.arange(0, 10, 0.01) # Time values from 0 to 10 with a step of 0.01
signal = 2 * np.sin(2 * np.pi * 1 * time) + 1 * np.sin(2 * np.pi * 2 * time)# Plot the original time series
plt.figure(figsize=(10, 4))
plt.subplot(2, 1, 1)
plt.plot(time, signal)
plt.title('Original Time Series')
plt.xlabel('Time')
plt.ylabel('Amplitude')# Perform the Fourier Transform
fourier_transform = np.fft.fft(signal)
frequencies = np.fft.fftfreq(len(signal), 0.01) # Frequency values (assuming a sampling interval of 0.01)# Plot the magnitude of the Fourier Transform
plt.subplot(2, 1, 2)
plt.plot(frequencies, np.abs(fourier_transform))
plt.title('Fourier Transform')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Magnitude')
plt.xlim(0, 5) # Limit the x-axis to show frequencies up to 5 Hzplt.tight_layout()
plt.show()在此代码中:
- 我们生成具有两个正弦分量的样本时间序列数据集。您应该将其替换为您自己的时间序列数据。
- 我们用来
np.fft.fft对时间序列数据执行傅里叶变换。 - 我们使用 计算相应的频率
np.fft.fftfreq。 - 我们创建两个子图:一个用于原始时间序列,另一个用于傅里叶变换的幅度。
- 最后,我们使用 显示图
plt.show()。
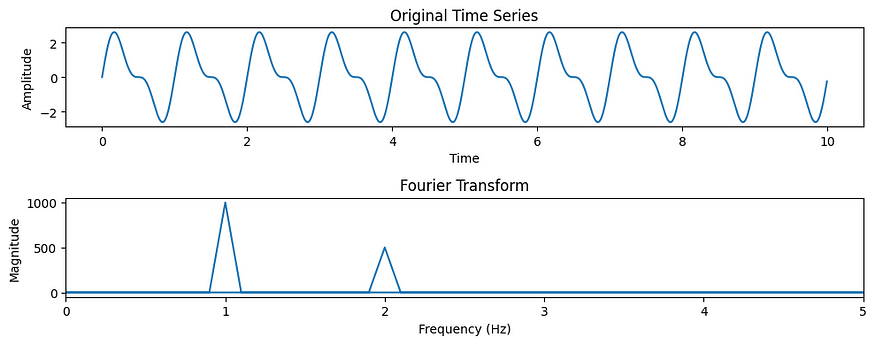
使用真实世界数据时,请确保将示例数据集替换为您自己的时间序列数据。上面的代码将为您提供原始时间序列和傅立叶变换幅度的图。您可以调整绘图参数和标签以满足您的特定需求。
六、结论
傅立叶变换最初是为信号处理而开发的,现已进入机器学习的核心。它从数据中分析和提取频率信息的能力在各种机器学习应用中非常宝贵,包括时间序列分析、自然语言处理、特征工程和增强深度学习模型。随着机器学习不断发展和扩大其视野,傅里叶变换仍然是一个强大的工具,使研究人员和从业者能够获得更深入的见解并开发更有效的算法。其多功能性和适应性使其成为现代机器学习工具箱中不可或缺的组成部分。
埃弗顿戈梅德博士
相关文章:

傅里叶变换及其在机器学习中的应用
一、介绍 傅立叶变换是一种数学技术,在各个科学和工程领域发挥着关键作用,其应用范围从信号处理到量子力学。近年来,它在机器学习领域发现了新的意义。本文探讨了傅里叶变换的基础知识及其在机器学习应用中日益增长的重要性。 …...

xorm源码学习
文章目录 XORM源码浅析及实践ORMORM vs. SQLXORM软件架构 ORM 引擎 Engine——DBM*core.DB Golang:database/sql 源码基本结构连接复用,提高性能。增加数据库连接池数量连接管理 database/sql主要内容:sql.DB创建数据库连接sql.Open()DB.conn…...

Vue3中的<script setup>和<script>的区别
相同点 在一个 Vue3 单文件组件 (SFC)中,<script setup> 和 <script> 它们各自最多只能存在一个。 不同点 <script setup> 这个脚本块将被预处理为组件的 setup() 函数,这意味着它将为每一个(也可以说每一次)组件实例都执行。 <…...
)
Docker笔记-Docker搭建最新版zabbix服务端(2023-07-31)
前言 一开始问chartgpt上,搭建的思路是对的,但命令和细节有问题,最后还是依靠StackOverflow解决的。一开始在amd的linux上搭建好docker版的zabbix,但放到arm的机器上就报错了,原因是指令集不匹配,最后跑到…...

QT配合CSS隐藏按钮
第一种方法 在Qt的CSS样式表中,使用 visibility 属性来隐藏按钮。设置 visibility 为 hidden 不可见,而设置为 visible 则可见。 隐藏所有 QPushButton QPushButton {visibility: hidden; }隐藏特定的按钮,用按钮的名称或样式类进行定位就…...

2023亚太地区数学建模C题思路分析+模型+代码+论文
目录 1.2023亚太地区各题思路模型:比赛开始后,第一时间更新,获取见文末名片 3 常见数模问题常见模型分类 3.1 分类问题 3.2 优化问题 详细思路见此名片,开赛第一时间更新 1.亚太地区数学建模ABC题思路模型:9比赛开…...
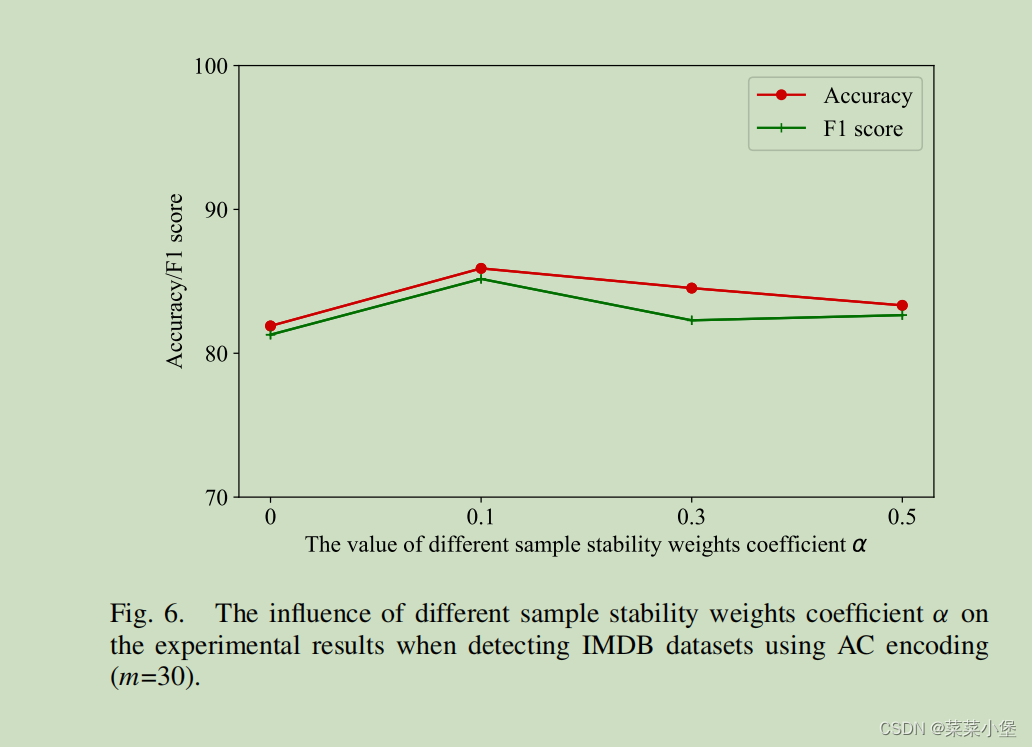
Linguistic Steganalysis in Few-Shot Scenario论文阅读笔记
TIFS期刊 A类期刊 新知识点 Introduction Linguistic Steganalysis in Few-Shot Scenario模型是个预训练方法。 评估了四种文本加密分析方法,TS-CSW、TS-RNN、Zou、SeSy,用于分析和训练的样本都由VAE-Stego生产(编码方式使用AC编码)。 实验是对比在少样…...
)
详细学习Pyqt5的4种项目部件(Item Widget)
Pyqt5相关文章: 快速掌握Pyqt5的三种主窗口 快速掌握Pyqt5的2种弹簧 快速掌握Pyqt5的5种布局 快速弄懂Pyqt5的5种项目视图(Item View) 快速弄懂Pyqt5的4种项目部件(Item Widget) 快速掌握Pyqt5的6种按钮 快速掌握Pyqt5的10种容器&…...
notepad++ 插件JSONView安装
1,前提 开发过程中经常需要处理json格式语句,需要对json数据格式化处理,因为使用的是虚拟机内开发,所以没法连接外网,只能在本地电脑下载插件后,然后上传到虚拟机中,进行安装使用。 2…...
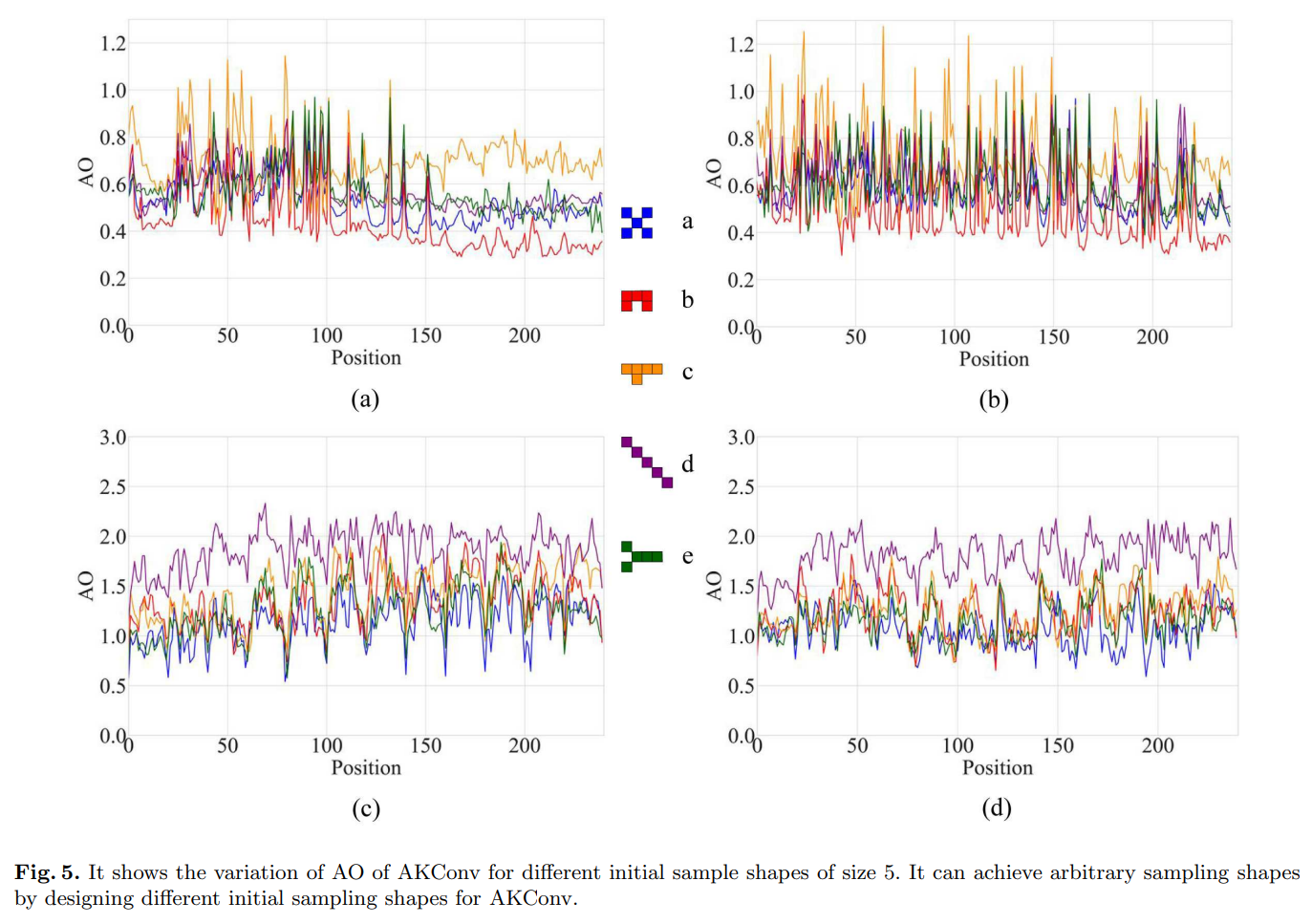
AKConv:具有任意采样形状和任意数目参数的卷积核
文章目录 摘要1、引言2、相关工作3、方法3.1、定义初始采样位置3.2、可变卷积操作3.3、扩展AKConv3.3、扩展AKConv 4、实验4.1、在COCO2017上的目标检测实验4.2、在VOC 712上的目标检测实验4.3、在VisDrone-DET2021上的目标检测实验4.4、比较实验4.5、探索初始采样形状 5、分析…...

如何使用C++开发集群服务
开发集群服务需要掌握以下技术: 分布式系统原理:了解集群的概念、工作原理、负载均衡、容错等相关概念。 网络编程:掌握Socket编程和HTTP协议等。 C编程:熟练掌握C语言的基础知识和STL等常用库。 多线程编程:了解线…...
docker安装以及idea访问docker
其他目录: docker 安装环境: https://blog.csdn.net/gd898989/article/details/134570167 docker 打包java包,并运行(有空更新) url “” docker 打包vue (有空更新) url “” docker 多服务 (…...

激光切割头组件中喷嘴的作用是什么
喷嘴是一个不可忽视的部件。尽管喷嘴并不起眼,却有着重要的作用;喷嘴一般是与激光切割头同轴的,且形状多样:圆柱形、锥形、缩放型等。 喷嘴的口径尺寸时不相同的,大口径的喷嘴对聚焦来的激光束没有很严苛的要求;而口径…...

腾讯云双11活动最后一天,错过再等一年!
腾讯云双11活动已经进入尾声,距离活动结束仅剩最后一天,记得抓住这次上云好时机,错过这次,就要等到下一年才能享受到这样的优惠力度了! 活动地址: 点此直达腾讯云双11活动主会场 活动详情: 1…...
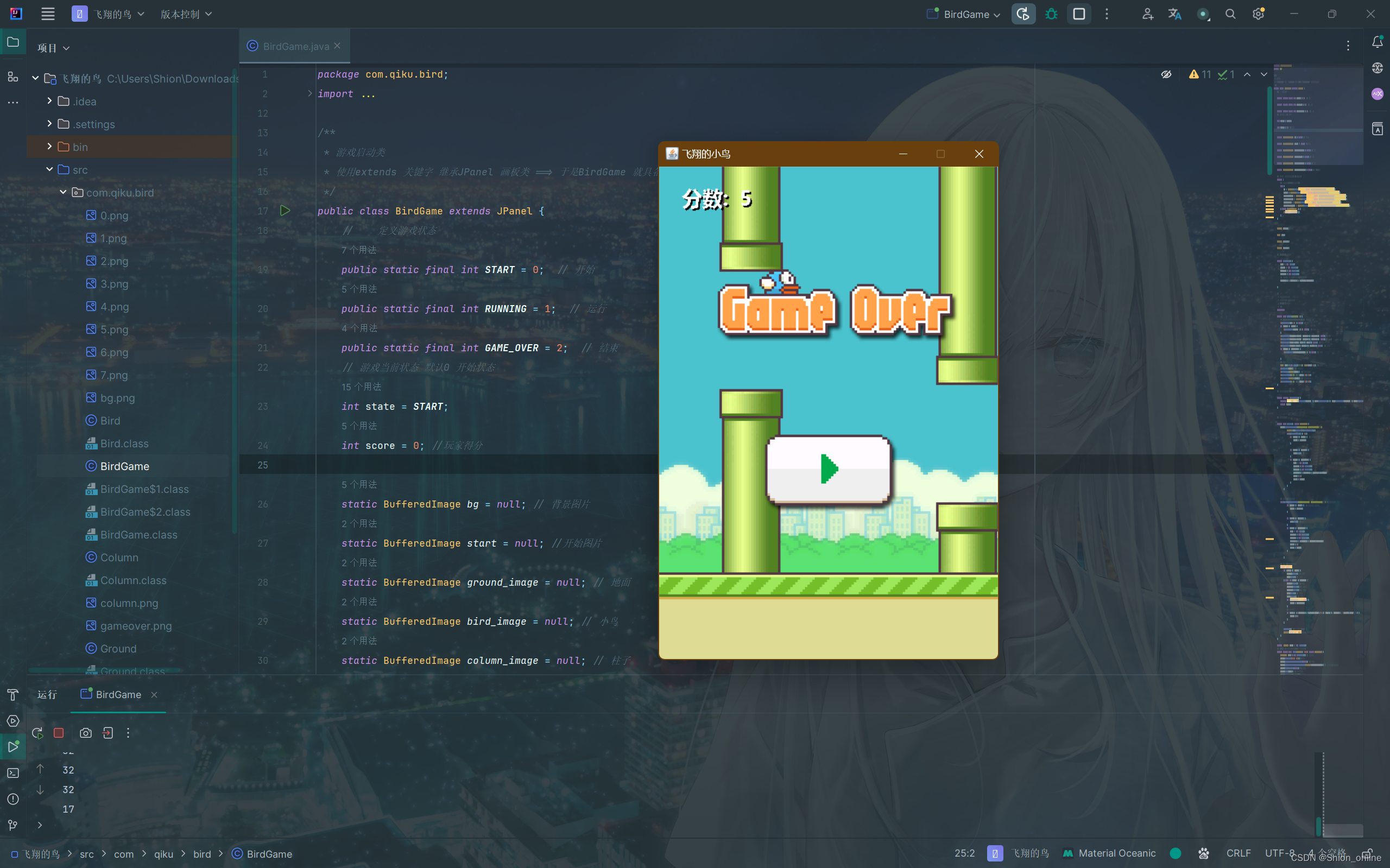
Java实现飞翔的鸟小游戏
Java实现飞翔的鸟小游戏 1.准备工作 创建一个新的Java项目命名为“飞翔的鸟”,并在src中创建一个包命名为“com.qiku.bird",在这个包内分别创建4个类命名为**“Bird”、“BirdGame”、“Column”、“Ground”,并向需要的图片**素材导入…...

Python网络请求初级篇:使用Requests库抓取和解析数据
在网络编程中,请求和接收数据是最常见的任务之一。Python的Requests库提供了丰富的功能,使得HTTP请求变得非常简单。在本文中,我们将了解如何使用Requests库发起HTTP请求,并解析返回的数据。 一、安装Requests库 首先࿰…...
详解API开发【电商平台API封装商品详情SKU数据接口开发】
1、电商API开发 RESTful API的设计 RESTful API是一种通过HTTP协议发送和接收数据的API设计风格。它基于一些简单的原则,如使用HTTP动词来操作资源、使用URI来标识资源、使用HTTP状态码来表示操作结果等等。在本文中,我们将探讨如何设计一个符合RESTfu…...

后端项目连接数据库-添加MyBatis依赖并检测是否成功
一.在pom.xml添加Mybatis相关依赖 在Spring Boot项目中,编译时会自动加载项目依赖,然后使用依赖包。 需要在根目录下pom.xml文件中添加Mybatis依赖项 <!-- Mybatis整合Spring Boot的依赖项 --> <dependency><groupId>org.mybatis.s…...

C++ CryptoPP使用RSA加解密
Crypto (CryptoPP) 是一个用于密码学和加密的 C 库。它是一个开源项目,提供了大量的密码学算法和功能,包括对称加密、非对称加密、哈希函数、消息认证码 (MAC)、数字签名等。Crypto 的目标是提供高性能和可靠的密码学工具,以满足软件开发中对…...
从实践角度深入探究数据驱动和关键字驱动测试方法!
数据驱动 数据驱动,指在软件测试领域当中的数据驱动测试(Data-Driven Testing,简称DDT)是⼀种软件测试⽅法,在不同的数据下重复执⾏相同顺序的测试步骤,测试脚本从数据源读取测试数据,⽽不使⽤…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

SQL注入篇-sqlmap的配置和使用
在之前的皮卡丘靶场第五期SQL注入的内容中我们谈到了sqlmap,但是由于很多朋友看不了解命令行格式,所以是纯手动获取数据库信息的 接下来我们就用sqlmap来进行皮卡丘靶场的sql注入学习,链接:https://wwhc.lanzoue.com/ifJY32ybh6vc…...
)
背包问题双雄:01 背包与完全背包详解(Java 实现)
一、背包问题概述 背包问题是动态规划领域的经典问题,其核心在于如何在有限容量的背包中选择物品,使得总价值最大化。根据物品选择规则的不同,主要分为两类: 01 背包:每件物品最多选 1 次(选或不选&#…...

P10909 [蓝桥杯 2024 国 B] 立定跳远
# P10909 [蓝桥杯 2024 国 B] 立定跳远 ## 题目描述 在运动会上,小明从数轴的原点开始向正方向立定跳远。项目设置了 $n$ 个检查点 $a_1, a_2, \cdots , a_n$ 且 $a_i \ge a_{i−1} > 0$。小明必须先后跳跃到每个检查点上且只能跳跃到检查点上。同时࿰…...
