element使用小结
1、tabel表头文字自定义效果(换行,不同颜色)
换行:
// 方法一
<el-table-columnprop="otherCost":label="'本期累计\n(元)'"> // 通过:label添加\n
</el-table-column>.xx .cell {white-space: pre-line;
}// 方法二
通过template标签
关于换行也可以使用width设置宽度进行换行,但不好控制换行字体个数(上少下多),而且整体列的宽度效果会不好,不能做到均分。
2、v-loading
v-loading可以在div上也可以在table上,但要想实现v-loding效果,所在标签不能使用v-show,包括父标签。
3、form
加了rules校验并且触发判断是change的input框不能限制输入类型(只能输入数字这种:οninput=“value=value.replace(/[^\d]/g,‘’)”),当用户输入不可输入的类型(比如只能输入数字你输入汉字字母)之后,rules将失效,输入提示不更新,点击submit也无法触发。
相关文章:

element使用小结
1、tabel表头文字自定义效果(换行,不同颜色) 换行: // 方法一 <el-table-columnprop"otherCost":label"本期累计\n(元)"> // 通过:label添加\n </el-table-column>.xx .cell {white-space: pre-…...
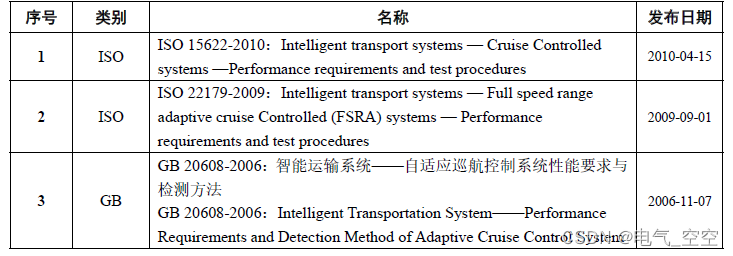
自动驾驶DCLC 功能规范
目录 1 概述Summary....................................................................................................... 4 1.1 目的Purpose....................................................................................................... 4 1.2 范围Ran…...
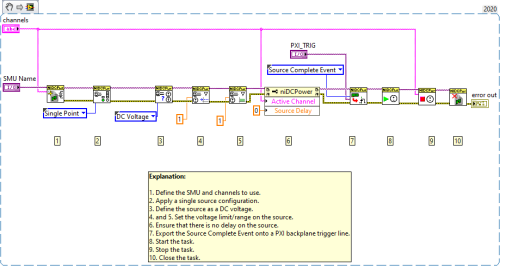
LabVIEW中将SMU信号连接到PXI背板触发线
LabVIEW中将SMU信号连接到PXI背板触发线 本文介绍如何将信号从PXI(e)SMU卡路由到PXI(e)机箱上的背板触发线。该过程涉及使用NI-DCPowerVI将SMU信号导出到PXI_TRIG线上。 在继续操作之前,请确保在开发PC上安装了兼容版…...

[蓝桥杯习题]———位运算、判断二进制1个数
⭐Hello!这里是欧_aita的博客。 ⭐今日语录:行动胜过一切。 ⭐个人主页:欧_aita ψ(._. )>⭐个人专栏: 数据结构与算法(内含蓝桥杯习题) MySQL数据库 位运算 位运算位运算的定义简单运用 实战刷题题目思路代码实现声…...

3DCAT为华东师大设计学院打造元宇宙数字虚拟学院
6月11日,华东师范大学设计学院在chi K11美术馆举办了一场别开生面的 2023 年本科毕业设计暨项目实践教学现场演示展。其中,元宇宙数字虚拟学院(一期)的现场发布会引起了现场震撼,吸引了众多观众的目光和参与。 该元宇宙…...

AIGC 3D即将爆发,混合显示成为产业数字化的生产力平台
2023年,大语言模型与生成式AI浪潮席卷全球,以文字和2D图像生成为代表的AIGC正在全面刷新产业数字化。而容易为市场所忽略的是,3D图像生成正在成为下一个AIGC风口,AIGC 3D宇宙即将爆发。所谓AIGC 3D宇宙,即由文本生成3D…...

时间序列预测实战(二十一)PyTorch实现TCN卷积进行时间序列预测(专为新手编写的自研架构)
一、本文介绍 本篇文章给大家带来的是利用我个人编写的架构进行TCN时间序列卷积进行时间序列建模(专门为了时间序列领域新人编写的架构,简单不同于市面上大家用GPT写的代码),包括结果可视化、支持单元预测、多元预测、模型拟合效…...

探索计算机视觉:深度学习与图像识别的融合
探索计算机视觉:深度学习与图像识别的融合 摘 要: 本文将探讨计算机视觉领域中的深度学习技术,并重点关注图像识别方面的应用。我们将介绍卷积神经网络(CNN)的原理、常用的图像数据集以及图像识别的实际应用场景&…...

屏蔽WordPress评论中长URL地址方法
由于WordPress是比较常见的CMS程序之一,所以很多网络营销推广也会基于WP去群发外链和广告信息。这里,我们可以通过屏蔽特定关键字、屏蔽特定字符的方式,或者是屏蔽评论内容的长短来限制评论。还有一个我们可以通过评论内容的URL地址的长度来屏…...

【教程】 一文部署配置并入门 Redis
综述 什么是Redis Redis官网——Redis.io Redis, 作为一个高性能的键值对数据库,主要应用于以下场景: 缓存系统:由于其高速读写能力,Redis 非常适合用作缓存系统,减少数据库负载。 会话存储(Session St…...

数据被锁住了?如何应对.mkp病毒的攻击
导言: 在数字时代的舞台上,.mkp勒索病毒如幽灵般悄然崭露头角,威胁着无数个体和组织的数据安全。本文将深度挖掘.mkp勒索病毒的狡猾本质,并为你揭示应对感染的独特方法,以及如何巧妙规避这个数字威胁。 如果您在面对被…...

【Shell】Shell基础学习
一、shell脚本 (1)第一个shell脚本 #!/bin/bash #this is a comment echo "hello world"一个shell脚本永远以“#!”开头,这是一个脚本开始的标记,它是告诉系统执行这个文件需要用某个解释器,后面的/bin/bash就是指明解释器的具体位置。 “#”开头是注释 …...

python文件读取
相对路径 读文件 打印txt文件 fopen(".\data.txt","r",encoding"utf-8") contentf.read() print(content) f.close()with open(".\data.txt","r",encoding"utf-8") as f:contentf.read()print(content)contentf…...

第16关 革新云计算:如何利用弹性容器与托管K8S实现极速服务POD扩缩容
------> 课程视频同步分享在今日头条和B站 天下武功,唯快不破! 大家好,我是博哥爱运维。这节课给大家讲下云平台的弹性容器实例怎么结合其托管K8S,使用混合服务架构,带来极致扩缩容快感。 下面是全球主流云平台弹…...

算法通关村第十二关|黄金挑战|最长公共前缀字符串压缩
1.最长公共前缀 原题:力扣14. 1.从前到后比较每个字符串的同一个位置。 public String longestCommonPrefix(String[] strs) {if (strs null || strs.length 0) {return "";}int length strs[0].length();int count strs.length;for (int i 0; i …...
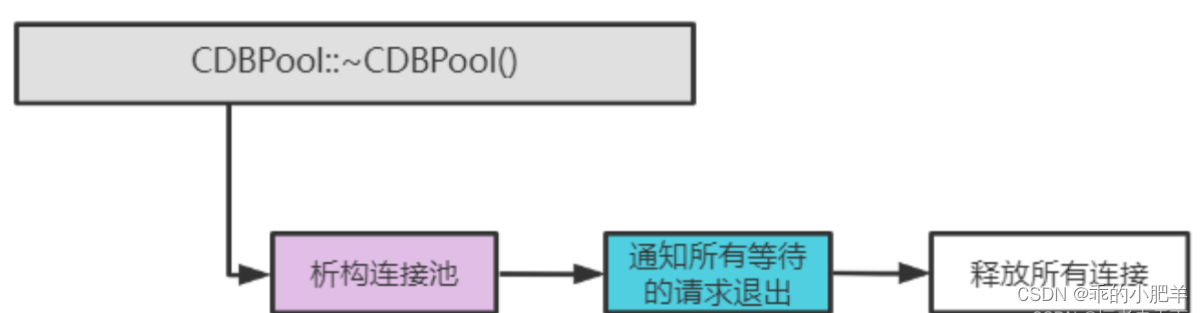
池式组件 ----- Mysql连接池的原理实现
前言 本文是mysql连接池的实现。学完mysql连接池之后,接下来会结合多线程来进行测试,看看使用连接池性能高,还是不要连接池性能高,具体能差多少。当然这是下一篇文章了哈哈哈哈哈。当前首要任务是学会连接池,会都不会…...
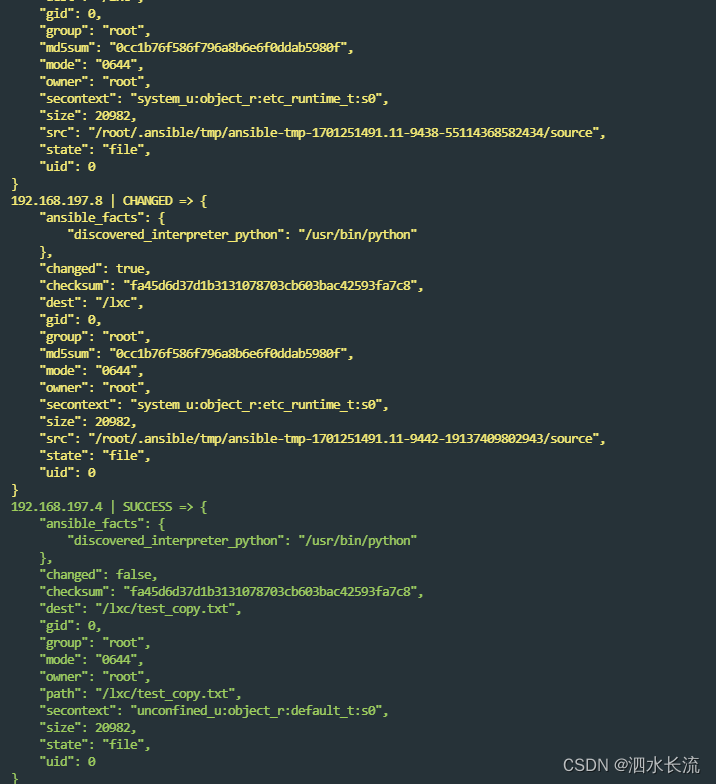
1.自动化运维工具Ansible的安装
1.物料准备 四台服务器,其中一个是主控机,三个为host 2.安装 在主控机上安装ansible 2.1 设置EPEL仓库 Ansible仓库默认不在yum仓库中,因此我们需要使用下面的命令启用epel仓库。 yum install epel-release -y2.2 执行安装命令 yum i…...

[个人笔记] Apache2.4配置TLS1.3安装openssl1.1.1
Linux - 运维篇 第二章 Apache2.4配置TLS1.3&安装openssl1.1.1 Linux - 运维篇系列文章回顾Apache2.4配置TLS1.3&安装openssl1.1.1参考来源 系列文章回顾 第一章 php-fpm编译和使用openssl扩展 Apache2.4配置TLS1.3&安装openssl1.1.1 [rootlocalhost ~]# yum ins…...

解密Kafka主题的分区策略:提升实时数据处理的关键
目录 一、Kafka主题的分区策略概述1.1 什么是Kafka主题的分区策略?1.2 为什么分区策略重要? 二、Kafka默认分区策略2.1 Round-Robin分区策略 三、自定义分区策略3.1 编写自定义分区器3.2 最佳实践:如何选择分区策略 四、分区策略的性能考量4.…...

GPT5大剧第二季开启,Sam Altman 重掌 OpenAI CEO 大权
OpenAl 最新公告: Sam Altman 重掌 OpenAI CEO 大权,公司迎来新的初始董事会 Mira Murati 出任 CTO,Greg Brockman 再次成为总裁。来看看CEO Sam Altman和董事会主席 Bret Taylor的最新发言。 2023年11月29日 以下是 CEO Sam Altman和董事会主席 Bret Taylor 今天下…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...
