算法的10大排序
10大排序算法--python
- 一颗星--选择排序
- 一颗星--冒泡排序
- 一颗星--插入排序
- 两颗星--归并排序(递归-难)
- 三颗星--桶排序
- 三颗星--计数排序
- 四颗星--基数排序
- 四颗星--快速排序,寻找标志位(递归-难)
- 四颗星--又是比较难的希尔排序
- 五颗星--堆排序
谁教你这么剪的 | 11大排序的原理讲解和Python源码剖析_哔哩哔哩_bilibili
一颗星–选择排序
自己看代码都能看懂
def xuanze_paixu(bb):
n=len(bb)
for i in range(n-1):
# 优化代码
min=i for j in range(i+1,n):
if bb[i]> bb[j]:
# 优化代码
min=j
bb[i], bb[min] = bb[min], bb[i] # bb[i],bb[j]=bb[j],bb[i]
return bb a=[0,4,0,9,2,8,4,0,1,8]
c=xuanzhe_paixu(a)
print(c)
一颗星–冒泡排序
自己看代码都能看懂
def maopao_paixu(bb):
n=len(bb)
# 左闭右开且递减
for i in range(n-1,-1,-1):
for j in range(0,i):
if bb[j]>bb[j+1]:
bb[j],bb[j+1]= bb[j+1],bb[j]
return bb
a=[7,3,9,8,7,4,9,4,2,4,1,8,7,4,9,1,8,4,7,9]
result=maopao_paixu(a)
print(result)
一颗星–插入排序
def charu_paixu(bb):
n=len(bb)
for i in range(1,n):
x=bb[i]
j=i-1
# 用j的话比较清除
while j>=0:
if x< bb[j]:
bb[j+1]=bb[j]
else:
break
bb[j]=x
j = j - 1
return bb
a=[7,3,9,8,7,4,9,4,2,4,1]
b=charu_paixu (a)
print(b)
两颗星–归并排序(递归-难)
直接给我cpu干蒙了
视频解释
排序算法:归并排序【图解+代码】_哔哩哔哩_bilibili
代码如下,有两种,多参考参考
def merge(a, start, mind, end):
l = start
bb = []
right = mind + 1 while l <= mind and right <= end:
if a[l] <= a[right]:
bb.append(a[l])
l += 1
else:
bb.append(a[right])
right += 1 bb.extend(a[l:mind+1])
bb.extend(a[right:end+1]) for j in range(start, end+1):
a[j] = bb[j - start] print(start, end, bb) def divide(a, start, end):
if start == end:
return mind = (start + end) // 2
divide(a, start, mind)
divide(a, mind+1, end)
merge(a, start, mind, end) a = [7, 3, 9, 8, 7]
divide(a, 0, 4) # 第二种
# 因为在Python中,列表是可变的数据类型,也就是说,当你传递一个列表到一个函数中时,你实际上是传递了这个列表的引用,而不是它的副本。这意味着如果你在函数中修改了这个列表,那么这个改变将会影响到原始的列表。
def merge_sort(arr, start, end):
if start >= end:
return
mid = (start + end) // 2
merge_sort (arr, start, mid)
merge_sort (arr, mid + 1, end)
merge (arr, start, mid, end) def merge(arr, start, mid, end):
left = arr[start:mid + 1]
right = arr[mid + 1:end + 1] i = j = 0
k = start while i < len (left) and j < len (right):
if left[i] <= right[j]:
arr[k] = left[i]
i += 1
else:
arr[k] = right[j]
j += 1
k += 1 while i < len (left):
arr[k] = left[i]
i += 1
k += 1 while j < len (right):
arr[k] = right[j]
j += 1
k += 1 a = [6, 1, 4, 1, 7]
merge_sort (a, 0, len (a) - 1)
print (a)
值得好好研究和阅读,比较像递归和分治
三颗星–桶排序
这个还是比较好理解的
from xuanzhe_paixu import xuanzhe_paixu as slect
def tong_paixu(a):
Min=min(a)
Max=max(a)
bucket_len=(Max-Min)//3+1 #将计算长度的线段分出来算出每个桶的长度
bucket= [[] for _ in range(3)]
for sum in a:
bucket[(sum-Min)//bucket_len].append(sum) # 相减能够计算线段,相除能够计算几倍桶长度
bb=[]
for arry in bucket:
result=slect(arry)
print(result)
for i in result:
bb.append(i)
return bb
b=[6,4,7,1,8,6,4,8,7]
d=tong_paixu(b)
print(d)
三颗星–计数排序
def jisu_paixu(arry):
Max=max(arry)+1
b=[0]*Max
a=[]
for each in arry:
b[each]+=1
for index,i in enumerate(b):
if i!=0:
for j in range(i):
a.append(index)
print(a)
d=[7,6,4,7,4,5,1,8,5,7,4,3,9,5,7,2,9,8,5,7,9,2,8,5,77,43,9]
jisu_paixu(d) # 第二种
def jisu_paixu1(arry):
Max = max (arry) + 1
b = [0] * Max
for each in arry:
b[each]+=1
print(b)
c=[]
for index in range(Max):
while b[index] >0:
c.append(index)
b[index]-=1
return c
d=[7,6,4,7,4,5,1,8,5,7,4,3,9,5,7,2,9,8,5,7,9,2,8,5,77,43,9]
result=jisu_paixu1(d)
print(result)
四颗星–基数排序
就是将得到的列表通过迭代,实现每次少一个数,将最后一个数按数字放入对应的桶中,需要创建一个二维列表,和清空一个二维列表,这个很重要
a = [[] for _ in range (10)]
for i in range (10):
a.append ([])
def jisu_paixu(arry):
a=[]
Max=max(arry)
base=1
for i in range (10):
a.append ([])
while base<Max:
n=0
for each in arry:
a[each//base%10].append(each)
print(a)
for list1 in a:
for i in list1:
arry[n]=i
n+=1
print(arry)
base*=10
a = [[] for _ in range (10)]
b=[3,214,1,24,13]
jisu_paixu(b)
四颗星–快速排序,寻找标志位(递归-难)
def kuaisu_paixu(a,start,end): if start==end: return flag=start binaliang=start+1 for i in range(start+1,end): if a[flag]>a[i]: a[i],a[binaliang]=a[binaliang],a[i] binaliang+=1 a[flag],a[binaliang-1]=a[binaliang-1],a[flag] flag=binaliang-1 print(a[flag],a[start:flag],a[flag+1:end]) kuaisu_paixu(a,start,flag) kuaisu_paixu(a,flag+1,end) a=[4,6,5,3,6,5,3,6,7,7,3,2,4,9,8,4,8,9,2,4,8,9,3,1,3,9] kuaisu_paixu(a,0,len(a)) print(a) # 第二种办法 import random
def kuaisu_paixu(a,start,end):
# random_index=random.randint(start,end-1)
# a[start],a[random_index]=a[random_index],a[start]
# 这个是用来随机快速排序的
flag=start
binaliang=start+1
for i in range(start+1,end):
if a[flag]>a[i]:
a[i],a[binaliang]=a[binaliang],a[i]
binaliang+=1
a[flag],a[binaliang-1]=a[binaliang-1],a[flag]
flag=binaliang-1
print(a[flag],a[start:flag],a[flag+1:end])
return flag
def paixu(a,start,end): if start==end:
return flag=kuaisu_paixu(a,start,end)
paixu(a,start,flag)
paixu(a,flag+1,end)
a=[4,6,5,3,6,5,3,6,7,7,3,2,4,9,8,4,8,9,2,4,8,9,3,1,3,9]
paixu(a,0,len(a))
print(a)
四颗星–又是比较难的希尔排序
这里面有两种方式,一个是切片排序,一个是从头排序
还有希尔排序就是特殊的插入排序,一定要多了解了解,加理解
# 希尔排序就是特殊的插入排序,间隔不在是1,而是gap和cha
def xier_paixu(a):
n=len(a)
gap=n//2
while gap>0:
for i in range(gap,n):
j=i
while j>=gap:
if a[j]<a[j-gap]:
a[j],a[j-gap]=a[j-gap],a[j]
else:
break
j-=gap gap=gap//2
a = [4, 7, 1, 9, 8, 4, 7, 9, 8, 1, 2, 7, 4, 9, 8, 1, 2, 4, 7, 1, 9, 84]
xier_paixu(a)
print(a) # 第二种
def xier_paixu1(alist, start, end):
n = end - start
cha = n // 2
while cha > 0:
for i in range(cha + start, end):
j = i
while j >= start+cha:
if alist[j] < alist[j - cha]:
alist[j], alist[j - cha] = alist[j - cha], alist[j]
else:
break
j -= cha
cha //= 2 return alist a = [4, 7, 1, 9, 8, 4, 7, 9, 8, 1, 2, 7, 4, 9, 8, 1, 2, 4, 7, 1, 9, 84]
start = 2
end = len(a)
print(xier_paixu1(a, start, end))
五颗星–堆排序
## 创建一个列表去执行大顶堆操作,便于排序
def fangwen_paixu(arry):
arry=[None]+arry
# 将列表进行自顶向下的堆排序,不能超过索引
for i in range(len(arry)//2,0,-1):
dui_paixu(arry,i,len(arry)-1)
# 将最顶堆顶端的数与最低端的数交换放入列表中,不断缩小最低端的索引
for i in range(len(arry)-1,0,-1):
arry[i],arry[1]=arry[1],arry[i]
dui_paixu(arry,1,i-1)
return arry
# 创建堆排序函数
##
def dui_paixu(a, start, end):
head=start
jiedian=start*2
while(jiedian<=end):
# 寻找叶子节点最大的值,与头节点比较,将最大的值放入到头节点中
if jiedian+1<=end and a[jiedian]<a[jiedian+1]:
jiedian+=1
if a[head]<a[jiedian]:
a[head],a[jiedian]=a[jiedian],a[head]
# 进行迭代,最后遍历完整个数组,形成大顶堆
head,jiedian=jiedian,jiedian*2
else:
break
# 创建一个测试fangwen_paixu函数
b=[4,6,5,3,6,5,3,6,7,7,3,2,4,9,8,4,8,9,2,4,8,9,3,1,3,9]
c=fangwen_paixu(b)
#把c列表里面的NONE去掉
c.pop(0)
print(c)
记得多看视频多理解理解,反复观看
相关文章:

算法的10大排序
10大排序算法--python 一颗星--选择排序一颗星--冒泡排序一颗星--插入排序两颗星--归并排序(递归-难)三颗星--桶排序三颗星--计数排序四颗星--基数排序四颗星--快速排序,寻找标志位(递归-难)四颗星--又是比较难的希尔排…...

“十道机器学习问题,帮助你了解基础知识和常见算法“
目录 简介: 1. 什么是机器学习?它与传统编程有什么不同之处?2. 请解释监督学习和无监督学习的区别。3. 什么是过拟合和欠拟合?如何解决这些问题?4. 请解释交叉验证在机器学习中的作用。5. 什么是特征选择?为…...
)
部署WAF安全应用防火墙(openresty部署)
使用NGINX+Openresty实现WAF功能 一、了解WAF 1.1 什么是WAF Web应用防护系统(也称:网站应用级入侵防御系统 。英文:Web Application Firewall,简称: WAF)。利用国际上公认的一种说法:Web应用 防火墙 是通过执行一系列针对HTTP/HTTPS的 安全策略 来专门为Web应用提供保…...
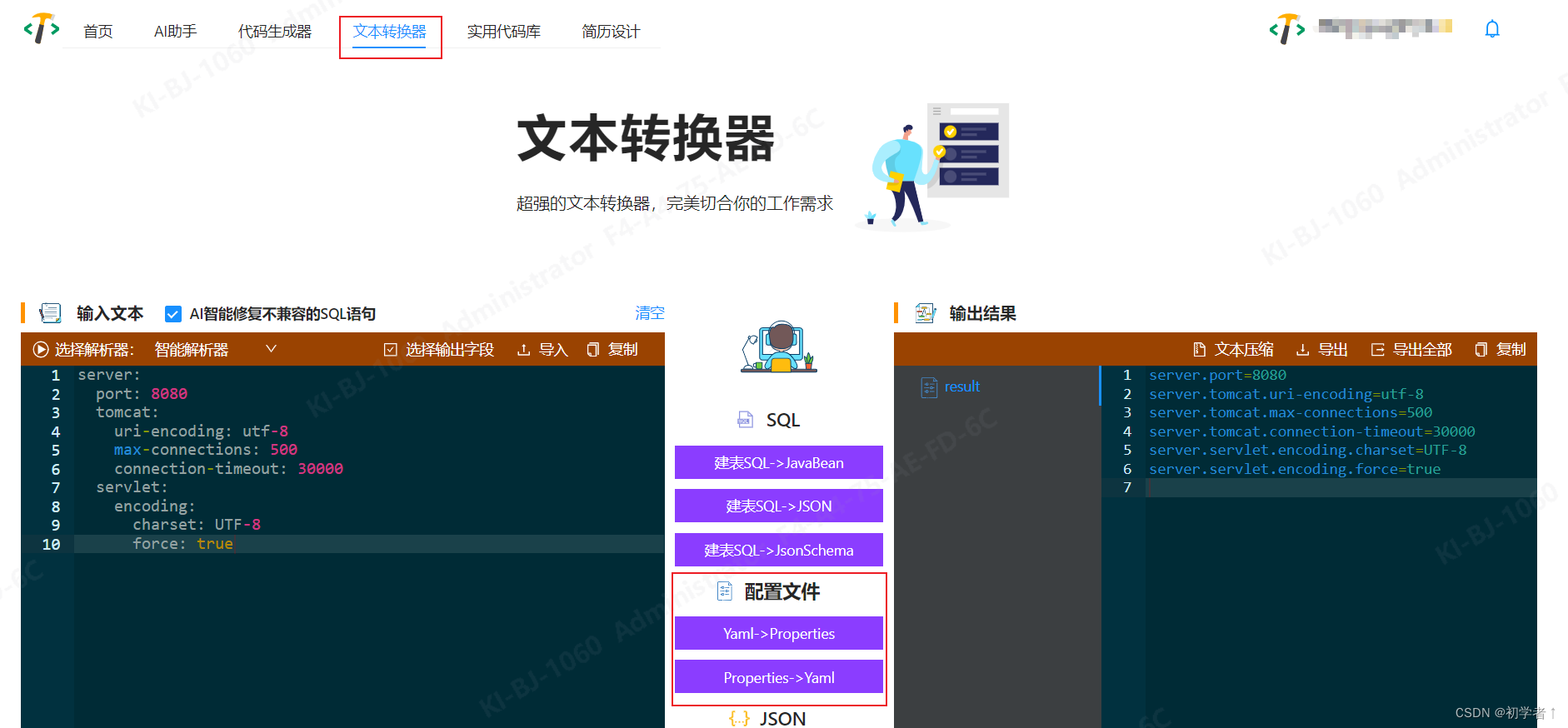
yml转properties工具
目前搜索到的大部分代码都存在以下问题: 复杂结构解析丢失解析后顺序错乱 所以自己写了一个,经过不充分测试,基本满足使用。可以直接在线使用 在线地址 除了yml和properties互转之外,还可以生成代码、sql转json等,可…...
zerotier 搭建 moon中转服务器 及 自建planet
搭建moon 服务器 环境准备 # 安装依赖 yum install wget gcc gcc-c git -y yum install json-devel -y# 下载及安装 curl -s https://install.zerotier.com/ | sudo bash节点ID 配置 配置moon.json文件 cd /var/lib/zerotier-one/# 导出依赖 zerotier-idtool initmoon ide…...
深入了解Rabbit加密技术:原理、实现与应用
一、引言 在信息时代,数据安全愈发受到重视,加密技术作为保障信息安全的核心手段,得到了广泛的研究与应用。Rabbit加密技术作为一种新型加密方法,具有较高的安全性和便捷性。本文将对Rabbit加密技术进行深入探讨,分析…...

Linux常用命令——mv命令
文章目录 1. 简介2. 命令格式3. 主要参数4. 常见用法及示例4.1 移动文件4.2 重命名文件4.3 交互式移动文件4.4 强制移动文件4.5 移动多个文件4.6 使用通配符移动文件 5. 注意事项6. 结论 1. 简介 mv 命令在Linux系统中用于移动文件或目录,同时也可以用于重命名文件…...

Panalog 日志审计系统 前台RCE漏洞复现
0x01 产品简介 Panalog是一款日志审计系统,方便用户统一集中监控、管理在网的海量设备。 0x02 漏洞概述 Panalog日志审计系统 sy_query.php接口处存在远程命令执行漏洞,攻击者可执行任意命令,接管服务器权限。 0x03 复现环境 FOFA…...

Android设置文字颜色渐变
项目中用到了很多文字颜色渐变的设计,因此做一下记录。 核心代码如下: /*** 统一文字渐变色设置* param colors 渐变色字符串数组* param positions 渐变色位置数组,可为空* param start 渐变起始点,可为空* param end 渐变结束…...
)
java基础面试题(二)
java后端面试题大全 3.JVM3.1 对象实例、类信息、常量、静态变量分别在运行时数据区的哪个位置?3.2 java类的加载流程3.3 java内存溢出什么时候会发生以及解决方法 3.JVM 3.1 对象实例、类信息、常量、静态变量分别在运行时数据区的哪个位置? 堆 对象实例、String常量池、基…...
php爬虫实现把目标页面变成自己的网站页面
最近又被烦的不行,琐事不断,要是比起懒来一个人比一个人懒,但是懒要转换成动力啊,能让自己真正的偷懒,而不是浪费时间。每天还是需要不断的学习的,才能更好的提高效率,把之前做的简单小功能爬虫…...

[c语言c++]手写你自己的swap交换函数
函数传参有按值传递,指针传递,引用传递,分别看一下三种情况下的交换函数如何书写,应该使用哪种最方便。 当书写一个交换两个值的 swap 函数时,我们可以分别使用按值传参、指针传参和引用传参的方式来实现。下面是示例和…...
)
技术类知识汇总(二)
在自己日常学习javaweb的过程中,做的一些笔记和总结,汇总如下: Springboot项目的静态资源(html,css,js等前端资源)默认存放目录为:classpath:/static classpath:/public classpath:/resources"三层架…...

简单好用!日常写给 ChatGPT 的几个提示词技巧
ChatGPT 很强,但是有时候又显得很蠢,下面是使用 GPT4 的一个实例: 技巧一:三重冒号 """ 引用内容使用三重冒号 """,让 ChatGPT 清晰引用的内容: 技巧二:角色设定…...
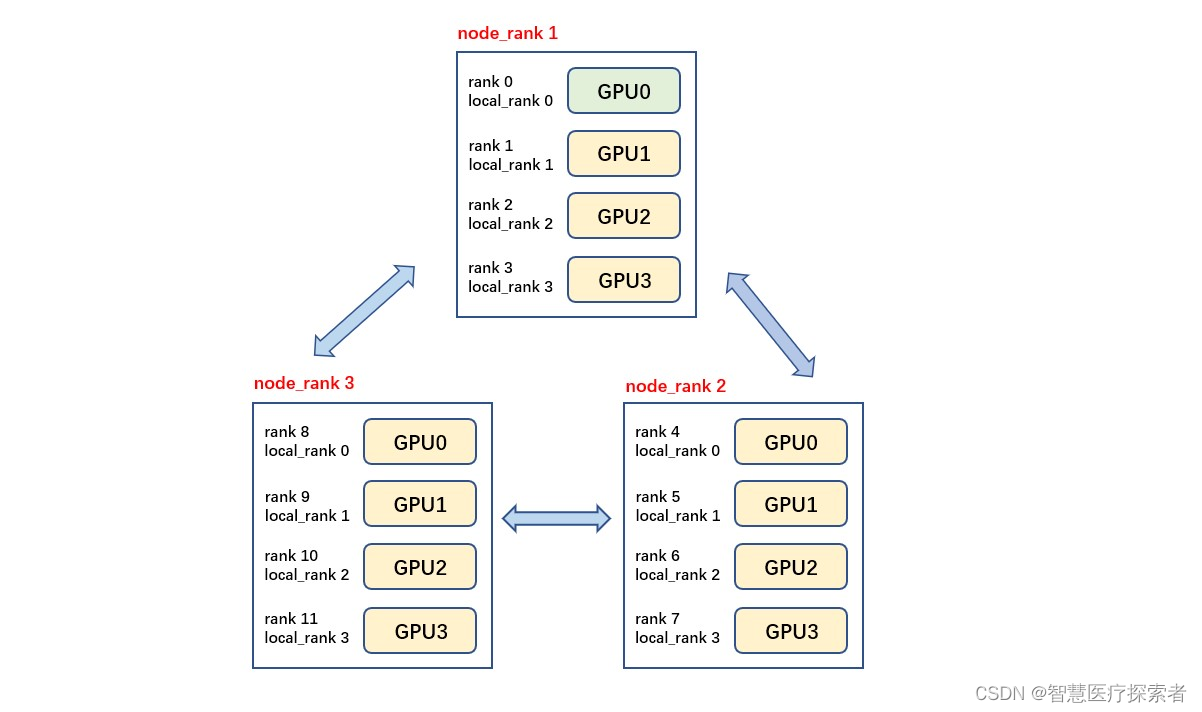
pytorch分布式训练
1 基本概念 rank:进程号,在多进程上下文中,我们通常假定rank 0是第一个进程或者主进程,其它进程分别具有1,2,3不同rank号,这样总共具有4个进程 node:物理节点,可以是一个…...
模型的创建、参数初始化、保存和加载)
【PyTorch】(三)模型的创建、参数初始化、保存和加载
文章目录 1. 模型的创建1.1. 创建方法1.1.1. 通过使用模型组件1.1.2. 通过继承nn.Module类 1.2. 模型组件1.2.1. 网络层1.2.2. 函数包1.2.3. 容器 1.3. 将模型转移到GPU 2. 模型参数初始化3. 模型的保存与加载3.1. 只保存参数3.2. 保存模型和参数 1. 模型的创建 1.1. 创建方法…...

高效开发之:判断复杂list中的对象属性是否包含某个值
技术使用:使用了Java 8引入的Stream API以及Optional类。这些特性用于简化集合的处理和减少空指针异常。 List<ResourceInfoDto> authData chatBase.getData();String baseName dto.getBaseName();Optional<ResourceInfoDto> authWithResourceCode a…...
MacOS + Android Studio 通过 USB 数据线真机调试
环境:Apple M1 MacOS Sonoma 14.1.1 软件:Android Studio Giraffe | 2022.3.1 Patch 3 设备:小米10 Android 13 一、创建测试项目 安卓 HelloWorld 项目: 安卓 HelloWorld 项目 二、数据线连接手机 1. 手机开启开发者模式 参考࿱…...
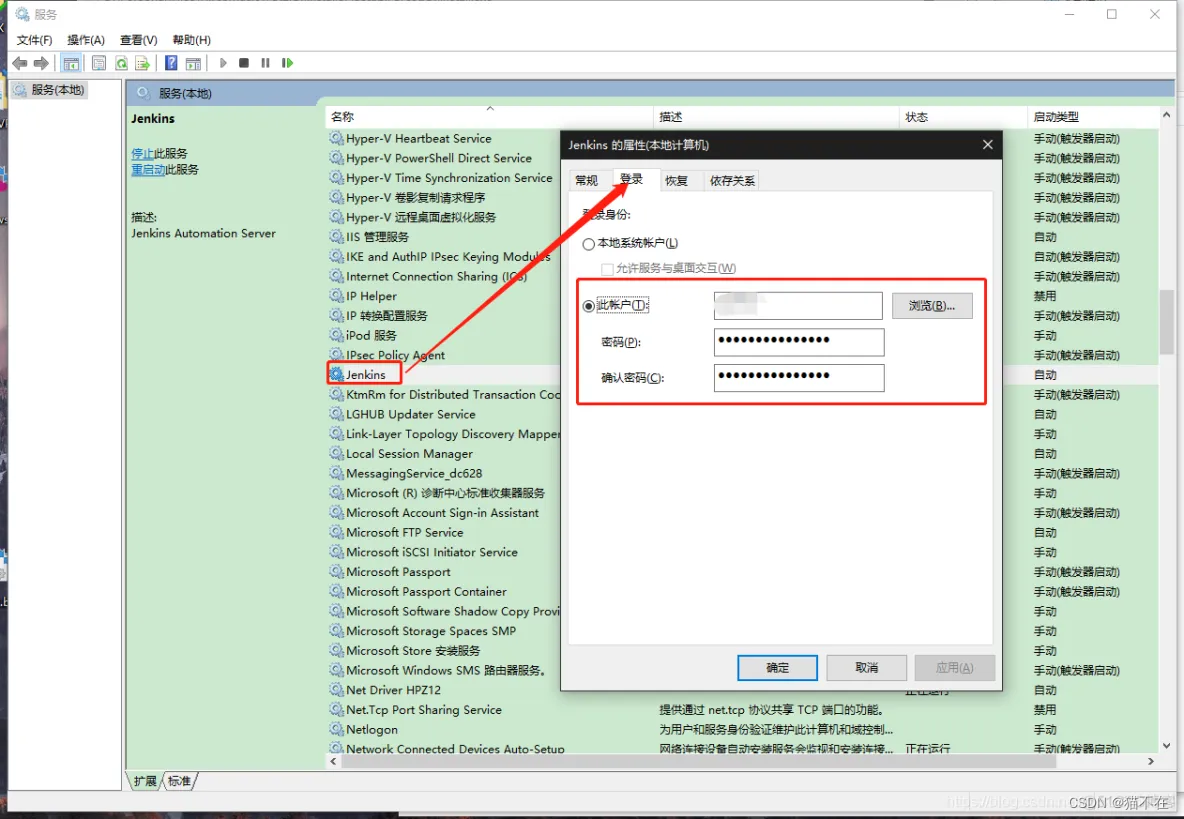
部署jekins遇到的问题
jdk问题 我用的jdk版本是21的结果版本太新了,启动jekins服务的时候总是报错最后在jekins的安装目录下面的jekinsErr.log查看日志发现是jdk问题最后换了一个17版本的就解决了。 unity和jekins jekins和Git源码管理 jekins和Git联动使用 我想让jekins每次打包的时…...
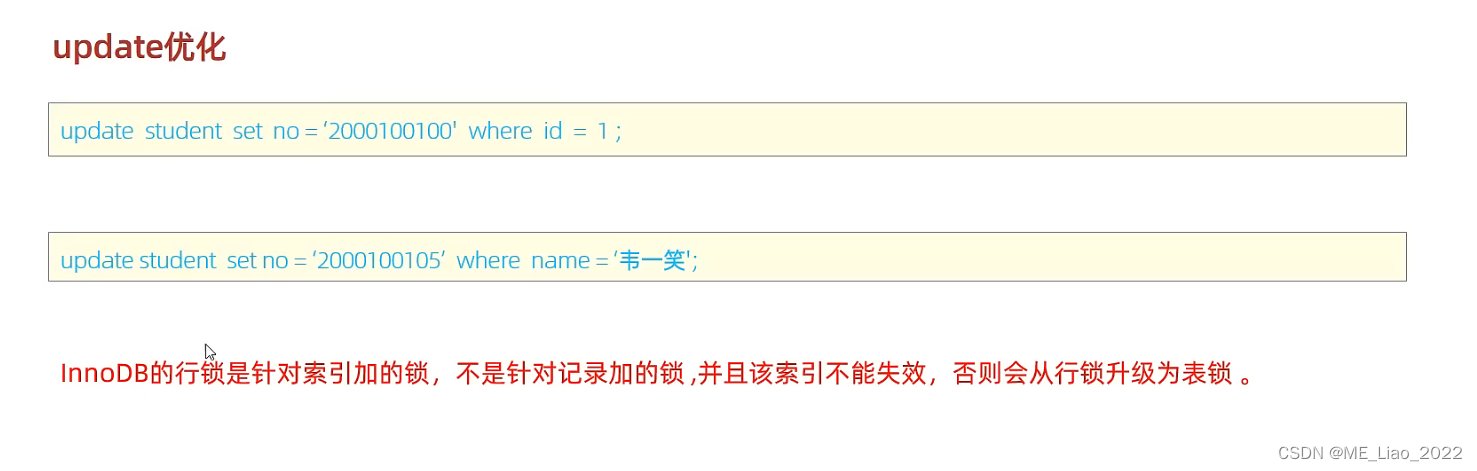
SQLY优化
insert优化 1.批量插入 手动事务提交 主键顺序插入,主键顺序插入性能高于乱序插入 2.大批量插入数据 如果一次性需要插入大批量数据,使用Insert语句插入性能较低,此时可以使用MYSQL数据库提供的load指令进行插入 主键优化 主键设计原则 …...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...
