代码随想录算法训练营第三十八天| 509 斐波那契数 70 爬楼梯 746 使用最小花费爬楼梯
509 斐波那契数
class Solution {public int fib(int n) {int f[] = new int[n + 5];f[0] = 0;f[1] = 1;for(int i = 2;i <= n;i++){f[i] = f[i - 1] + f[i - 2];}return f[n];}
}时间复杂度O(n)
空间复杂度O(n)
70 爬楼梯
class Solution {public int climbStairs(int n) {int f[] = new int[n + 5];f[0] = 0;f[1] = 1;f[2] = 2;for(int i = 3;i <= n;i++){f[i] = f[i - 1] + f[i - 2];}return f[n]; }
}时间复杂度O(n)
空间复杂度O(n)
746 使用最小花费爬楼梯
class Solution {public int minCostClimbingStairs(int[] cost) {int f[] = new int[cost.length + 1];//代表爬到此楼梯需要的最小花费f[0] = 0;f[1] = 0;for(int i = 2;i <= cost.length;i++){f[i] = Math.min(f[i - 1] + cost[i - 1],f[i - 2] + cost[i - 2]);}return f[cost.length];}
}时间复杂度O(n)
空间复杂度O(n)
相关文章:

代码随想录算法训练营第三十八天| 509 斐波那契数 70 爬楼梯 746 使用最小花费爬楼梯
509 斐波那契数 class Solution {public int fib(int n) {int f[] new int[n 5];f[0] 0;f[1] 1;for(int i 2;i < n;i){f[i] f[i - 1] f[i - 2];}return f[n];} } 时间复杂度O(n) 空间复杂度O(n) 70 爬楼梯 class Solution {public int climbStairs(i…...

windows 此系统禁止运行脚本报错处理
windows 此系统禁止运行脚本报错处理 start 在命令行中运行执行的脚本,运行原理可以参考文章 《》本文主要介绍,如何处理window默认的对脚本运行的限制。 详细说明 出现报错如下: 主要原因就是系统默认禁止了在 powershell 环境下某些脚…...
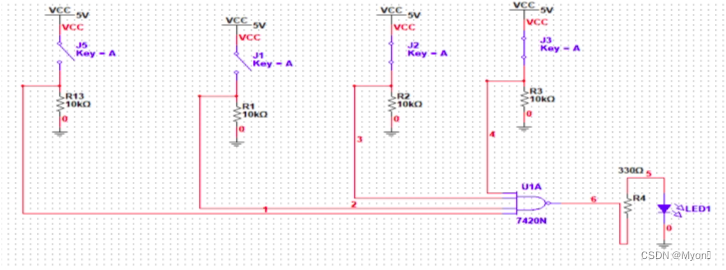
西南科技大学数字电子技术实验一(数字信号基本参数与逻辑门电路功能测试及FPGA 实现)FPGA部分
一、 实验目的 1、掌握基于 Verilog 语言的 diamond 工具设计全流程。 2、熟悉、应用 Verilog HDL 描述数字电路。 3、掌握 Verilog HDL 的组合和时序逻辑电路的设计方法。 4、掌握“小脚丫”开发板的使用方法。 二、 实验原理 与门逻辑表达式:Y=AB 原理仿真图: 2 输入…...

List系列集合
List系列集合特点:有序,可重复,有索引 ArrayList:有序,可重复,有索引 LinkedList:有序,可重复,有索引 (底层实现不同!适合的场景不同!…...
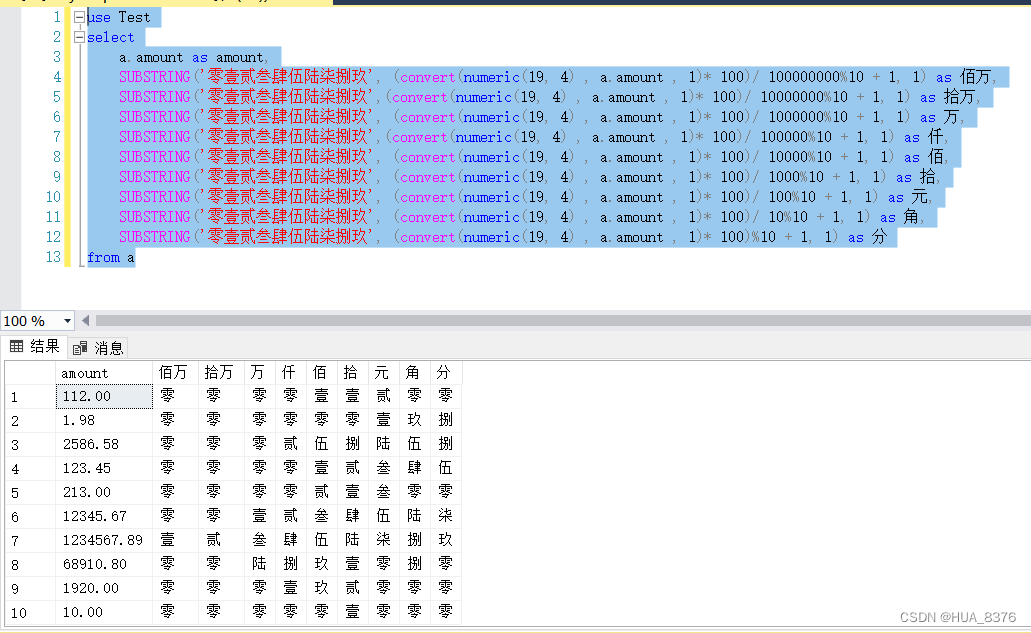
SQL 金额数值转换成中文大写
需求:将金额转换成中文大写格式填入单据合计行: _佰_拾_万_仟_佰_拾_元_角_分 1234567.89 壹佰贰拾叁万肆仟伍佰陆拾柒元捌角玖分 1.函数转换 drop function n2C;CREATE FUNCTION n2C (num numeric(14,2)) RETURNS VARCHAR(20) AS BEGIN …...

在Linux上安装KVM虚拟机
一、搭建KVM环境 KVM(Kernel-based Virtual Machine)是一个基于内核的系统虚拟化模块,从Linux内核版本2.6.20开始,各大Linux发行版就已经将其集成于发行版中。KVM与Xen等虚拟化相比,需要硬件支持的完全虚拟化。KVM由内…...

软件设计之原型模式
原型模式是从一个对象再创建另一个可定制的对象,而且不需要知道任何创建的细节。拷贝分浅拷贝和深拷贝。浅拷贝无法拷贝引用对象。在面试的时候,我们会投多家公司,根据岗位的不同我们会适当调整。使用原型模式可以快速达到需求,下…...
Android之高级UI
系统ViewGroup原理解析 常见的布局容器: FrameLayout, LinearLayout,RelativeLayoout,GridLayout 后起之秀:ConstraintLayout,CoordinateLayout Linearlayout Overrideprotected void onMeasure(int widthMeasureSpec, int heightMeasureSpec) {if (mOrientation …...

Qt:解决跨线程调用socket/IO类,导致报错的问题
Qt有很多IO相关的类,比如说QTcpSocket、QFile,总的来说,在Qt的框架内使用,还是非常方便的。 但是用过其他框架IO类的人,可能有一个很不习惯,就是Qt的所有IO类,都不推荐或者不可以跨线程操作&…...

长沙电信大楼火灾调查报告发布:系烟头引发。FIS来护航安全
近日,长沙电信大楼的火灾调查报告引起广泛关注。调查发现,火灾是由未熄灭的烟头引发,烟头点燃了室外平台的易燃物,迅速蔓延至整个建筑。这起悲剧再次提醒我们,小小的疏忽可能酿成大灾难。但如果我们能及时发现并处理这…...

【Web系列二十七】Vue实现dom元素拖拽并限制移动范围
目录 需求 拖拽功能封装 使用拖拽功能 vite-env.d.ts main.ts test.vue 需求 dom元素拖拽并限制在父组件范围内 拖拽功能封装 export const initVDrag (vue) > {vue.directive(drag, (el) > {const oDiv el // 当前元素oDiv.onmousedown (e) > {let target…...

【IEEE独立出版】2024第四届神经网络、信息与通信工程国际学术会议(NNICE 2024)
2024第四届神经网络、信息与通信工程国际学术会议(NNICE 2024) 2024 4th International Conference on Neural Networks, Information and Communication Engineering 2024第四神经网络、信息与通信工程国际学术会议(NNICE 2024࿰…...

docker 推送tar包到远程仓库
tar 包 推送到远程仓库的步骤 - 导入镜像(docker load -i 镜像名称)示例:docker load -i yiyi-admin.tar- 打标签(docker tag 镜像id registry.cn-hangzhou.aliyuncs.com/空间名称/镜像名称:版本号)示例:docker tag $image_id reg…...

全志XR806基于FreeRTOS下部署竞技机器人先进模糊控制器
前言 很荣幸参与到由“极术社区和全志在线联合组织”举办的XR806开发板试用活动。本人热衷于各种的开发板的开发,同时更愿意将其实现到具体项目中。秉承以上原则,发现大家的重心都放在开发中的环境构建过程,缺少了不少实际应用场景的运用&am…...

python动态加载内容抓取问题的解决实例
问题背景 在网页抓取过程中,动态加载的内容通常无法通过传统的爬虫工具直接获取,这给爬虫程序的编写带来了一定的技术挑战。腾讯新闻(https://news.qq.com/)作为一个典型的动态网页,展现了这一挑战。 问题分析 动态…...

系列二十三、将一个第三方的类配置成bean的方式
一、将一个第三方的类配置成bean的方式 1.1、概述 日常的JavaEE开发中,难免不会遇到需要使用第三方的类的情况,比如:MyBatisPlus、RedisTemplate、DruidDataSource...,这些外部组件是不同的组织或个人提供的,我们为什…...
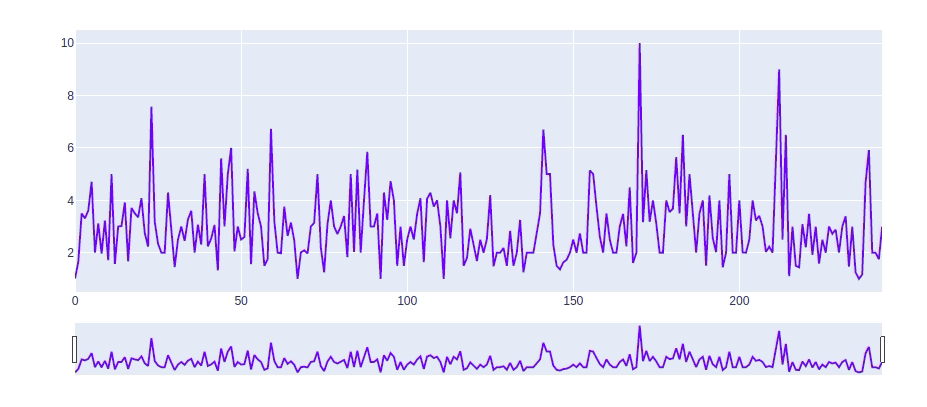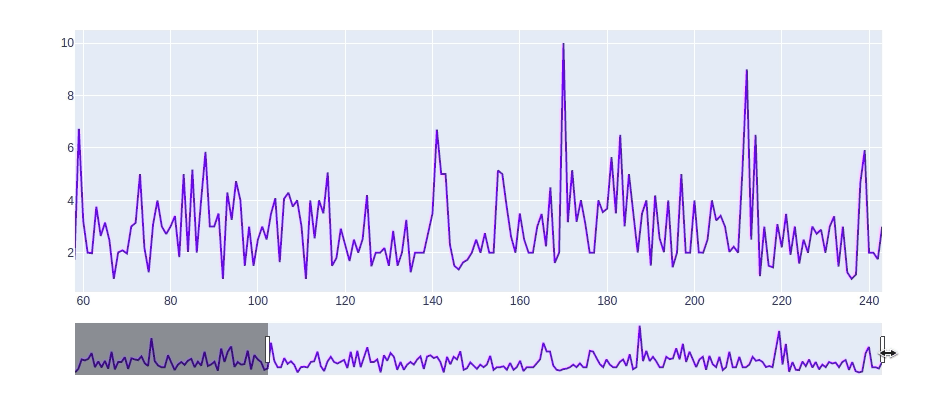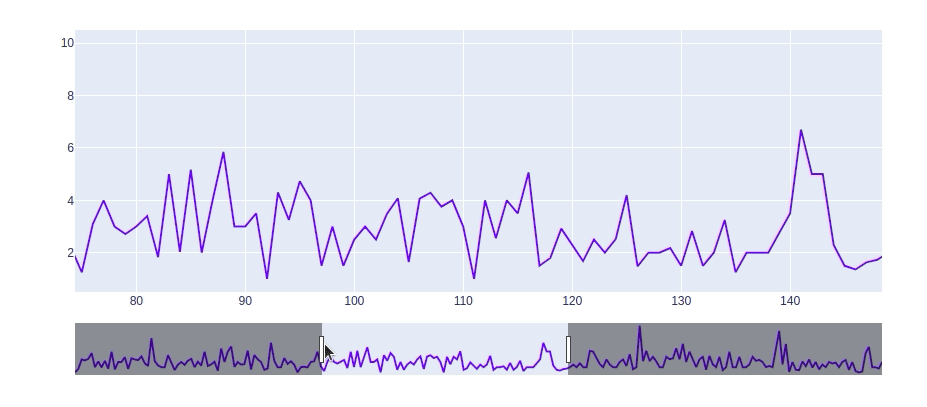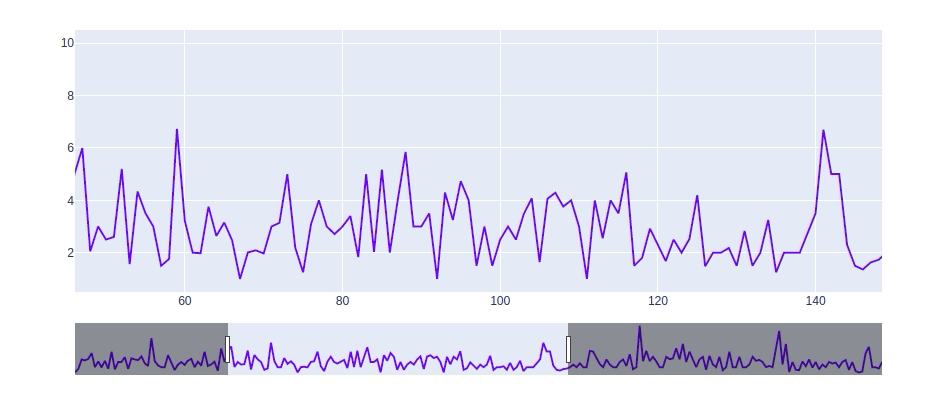
【长文干货】Python可视化教程
文章目录 数据介绍Matplotlib散点图折线图柱形图直方图 Seaborn散点图折线图柱形图直方图 Bokeh散点图折线条形图交互式 Plotly基本组合优化:定制化下拉菜单 总结 数据介绍 在这个小费数据集中,我们记录了20世纪90年代初期餐厅顾客在两个半月内给出的小…...
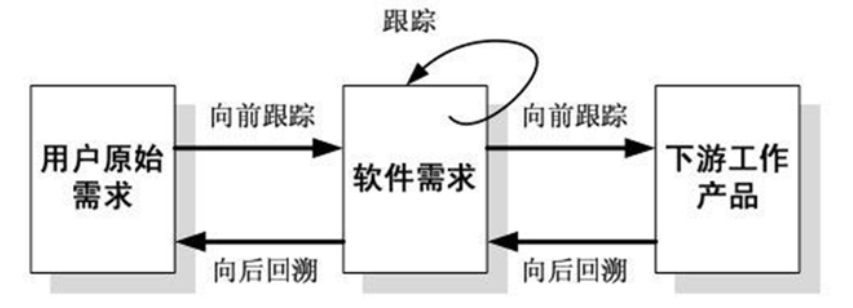
软件工程--需求工程--学习笔记(超详细)
软件需求工程是软件开发周期的第一个阶段,也是关系到软件开发成败最关键阶段,本章讲解需求的基础知识和需求工程的关键活动。这些知识对于结构化方法、面向对象方法、面向服务方法等都是适用的 本文参考教材:沈备军老师的《软件工程原理》 目…...

TemplateHit中提取query和hit比对上序列索引的映射字典
template_hits(Sequence[TemplateHit]数据格式)来自结构数据库搜索结果 python运行hhsearch二进制命令的包装器类 映射索引计算:TemplateHit 中含有 indices_query,需要换算成在原始query序列中的index,hit 中indices_hit 需要减去最小index…...
富必达API:一站式无代码开发集成电商平台、CRM和营销系统
一站式无代码开发的连接解决方案 电子商务、客户服务系统以及其它商业应用,是现代企业运营的重要部分。然而,将这些系统进行有效的整合往往需要复杂的API开发,这对很多企业来说是一个巨大的挑战。富必达API以其一站式的无代码开发解决方案&a…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...
