py 启动默认浏览器
要在Python中启动默认浏览器,可以使用第三方库如webbrowser或pyperclip,也可以使用操作系统特定的命令行调用。以下是几个不同的方法:
- 使用webbrowser库:
import webbrowser
webbrowser.open("http://example.com")
这将打开默认浏览器并导航到指定的URL。
- 使用pyperclip库复制网页链接并打开浏览器:
首先,您需要安装pyperclip库(可以使用pip进行安装):
pip install pyperclip
然后,您可以使用以下代码复制网页链接并将其粘贴到默认浏览器中:
import pyperclip
url = "http://example.com"
pyperclip.copy(url)
os.system('start %s' % os.path.join(os.getenv('HOME'), 'Desktop', 'default_browser.exe')) # Windows系统,您需要安装并配置默认浏览器快捷方式到桌面
注意,上述代码假定您已经将默认浏览器配置为在桌面创建一个快捷方式,并使用“start”命令打开它。您需要根据您的操作系统和配置进行相应的修改。
- 使用操作系统特定的命令行调用:
在Windows系统上,您可以使用以下代码调用默认浏览器打开指定的网页链接:
import os
os.system('start "Your Web Browser" http://example.com')
在macOS和Linux系统上,可以使用以下代码调用默认浏览器打开指定的网页链接:
在macOS上:
import subprocess
subprocess.call(['open', 'http://example.com'])
在Linux上:
import subprocess
subprocess.call(['xdg-open', 'http://example.com'])
请注意,这些方法可能需要您的系统配置特定于浏览器或Python库,并且可能需要使用管理员权限或特定的环境变量。确保您已经正确配置了默认浏览器和Python环境。
相关文章:

py 启动默认浏览器
要在Python中启动默认浏览器,可以使用第三方库如webbrowser或pyperclip,也可以使用操作系统特定的命令行调用。以下是几个不同的方法: 使用webbrowser库: import webbrowser webbrowser.open("http://example.com")这…...

scala可变参数列表使用
在Scala中,可以使用可变参数列表(varargs)来定义一个函数,以接受可变数量的参数。示例如下: def printArgs(args: String*): Unit {args.foreach(println) }// 使用可变参数列表 printArgs("Hello", "…...

经验分享:JMeter控制RPS
一、前言 RPS (Request Per Second)一般用来衡量服务端的吞吐量,相比于并发模式,更适合用来摸底服务端的性能。我们可以通过使用 JMeter 的常数吞吐量定时器来限制每个线程的RPS。对于RPS,我们可以把他理解为我们的TPS,我们就…...

JavaScript中的for循环你用对了吗?
🌈个人主页:前端青山 🔥系列专栏:JavaScript篇 🔖人终将被年少不可得之物困其一生 依旧青山,本期给大家带来JavaScript篇专栏内容:JavaScript-for循环 目录 循环结构 循环思想(三要素) 实现…...
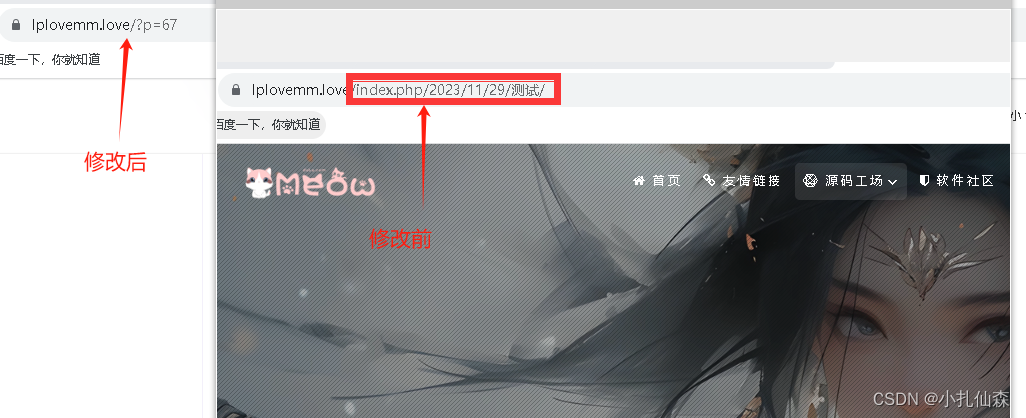
WordPress(10)解决中文连接问题
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、修改的前后二、自定义结构讲明三、修改方法前言 提示:这里可以添加本文要记录的大概内容: 1.中文连接如:http://www.lplovemm.love/2023/11/12/测试 2.这种连接在提交sitemap收录的时…...

2023年小美赛认证杯国际赛A题解题思路+数据分享版+部分代码
小美赛作为一个与美赛高度相似的比赛,通常作为很多队伍的美赛练手赛,本次也将尝试帮助大家对A题进行求解,希望能够对大家有所帮助。真实的选题人数评估预计明天进行公布 难度 B>DC>A 选题 A>B>D>C 问题A(MCM&am…...

删除list中除最后一个之外所有的数据
1.你可以新建一个list List<Integer> listnew ArrayList<>();int i0;while (i<100){list.add(i);}List<Integer> subList list.subList(list.size()-1, list.size());System.out.println("原list大小--"list.size());System.out.println("…...
北京筑龙助力中粮集团采购供应链改革加速跑
11月6日,在第六届中国国际进口博览会(简称“进博会”)上,中粮集团与来自全球的供应商签约进口农产品,金额超百亿美元,签约额、进口量、进口来源地覆盖范围均创历史新高。 这只是中粮集团落实集中采购&…...
)
SpringBoot学习笔记-实现微服务:匹配系统(中)
笔记内容转载自 AcWing 的 SpringBoot 框架课讲义,课程链接:AcWing SpringBoot 框架课。 CONTENTS 1. 同步玩家位置1.1 游戏信息的记录1.2 实现多线程同步移动 2. 同步碰撞检测3. 实现游戏结束界面4. 持久化游戏状态4.1 创建数据库表4.2 保存游戏对局信息…...
[Python实现])
【复杂网络建模】——基于代理的社会网络建模(Agent-Based Modeling,ABM)[Python实现]
目录 一、复杂网络建模方法 二、基于代理的社会网络建模实现及Python实现代码 一、复杂网络建模方法 复杂网络是一种由大量相互连接的元素(节点或顶点)组成的网络结构,这些连接通常是非常复杂和动态的。这些网络可以在各种领域中发现,包括社交网络、生物学系统、信息技术…...
)
RSA实现中弱密钥漏洞分析(Analyzing Weak Key Vulnerabilities in RSA Implementation)
点我完整下载:《RSA实现中弱密钥漏洞分析》本科毕业论文一万字.doc RSA实现中弱密钥漏洞分析 "Analyzing Weak Key Vulnerabilities in RSA Implementation" 目录 目录 2 摘要 3 关键词 4 第一章 引言 4 1.1 研究背景 4 1.2 研究目的 5 1.3 研究意义 6 第…...
| 图与网络分析(最大流问题,最小费用最大流问题))
【管理运筹学】背诵手册(六)| 图与网络分析(最大流问题,最小费用最大流问题)
六、图与网络分析 最大流问题 最大流问题的数学规划模型为: max v f 12 f 13 { f 12 f 13 − f 57 − f 67 0 f 13 f 23 f 34 f 35 . . . 0 ≤ f i j ≤ c i j \max vf_{12}f_{13}\\ \begin{cases} f_{12}f_{13}-f_{57}-f_{67}0 \\ f_{13}f_{23}f_{34}f…...

C语言之结构体详解
C语言之结构体详解 文章目录 C语言之结构体详解1. 结构体类型的声明2. 结构体变量的创建和初始化3. 结构体的特殊声明4. 结构体的自引用结构体的自引用匿名结构体的自引用 5. 结构体内存对齐5.1 练习一5.2 练习三 6. 为什么存在内存对⻬? 1. 结构体类型的声明 struct tag {me…...

学习canvas
Canvas是一个基于像素的渲染引擎,它使用JavaScript API在画布上绘制图像。以下是它的一些优点和缺点: 优点: Canvas的渲染速度快,适合处理大量图像和高度动态的图像。 可以直接操作像素,从而能够创建出高质量、流畅的…...

浏览器的渲染原理
以下内容来源于渡一前端大师课,仅作个人学习记录。 渲染的第一步是 解析HTML 解析过程中遇到CSS解析CSS,遇到JS执行JS。为了提高解析效率,浏览器在开始解析之前,会启动一个预解析的线程,率先下载HTML中的外部CSS文件和…...

从 JSON 转 Java 实体的多种方法详解
将 JSON 数据转换为 Java 对象是现代应用程序开发中常见的任务。在 Java 中,有多种方法可以实现这一目标。本文将详细介绍几种常见的方法,以及它们的优缺点。 1. 手动映射(Manual Mapping) 手动映射是最基础的方法之一ÿ…...
数据库的多表查询(MYSQL)表表联立
根据以上三张表格,对三张表格进行不同的联立,查询并显示符合条件的内容。 1. 查出至少有一个员工的部门。显示部门编号、部门名称、部门位置、部门人数。 mysql> SELECT d.deptno AS 部门编号, d.dname as 部门名称, d.loc as 部门位置, COUNT(e.emp…...
)
P8650 [蓝桥杯 2017 省 A] 正则问题(dfs )
多重括号,利用回溯来对上一层括号中的内容进行反馈 实现: 若为 x 长度加一 若为 ( 进入递归计算 (计算相当于子表达式) 若为 ) 结束当前递归 若为 | …...

【ESP32】手势识别实现笔记:红外温度阵列 | 双三次插值 | 神经网络 | TensorFlow | ESP-DL
目录 一、开发环境搭建与新建工程模板1.1、开发环境搭建与卸载1.2、新建工程目录1.3、自定义组件 二、驱动移植与应用开发2.1、I2C驱动移植与AMG8833应用开发2.2、SPI驱动移植与LCD应用开发2.3、绘制温度云图2.4、启用PSRAM(可选)2.5、画面动静和距离检测…...
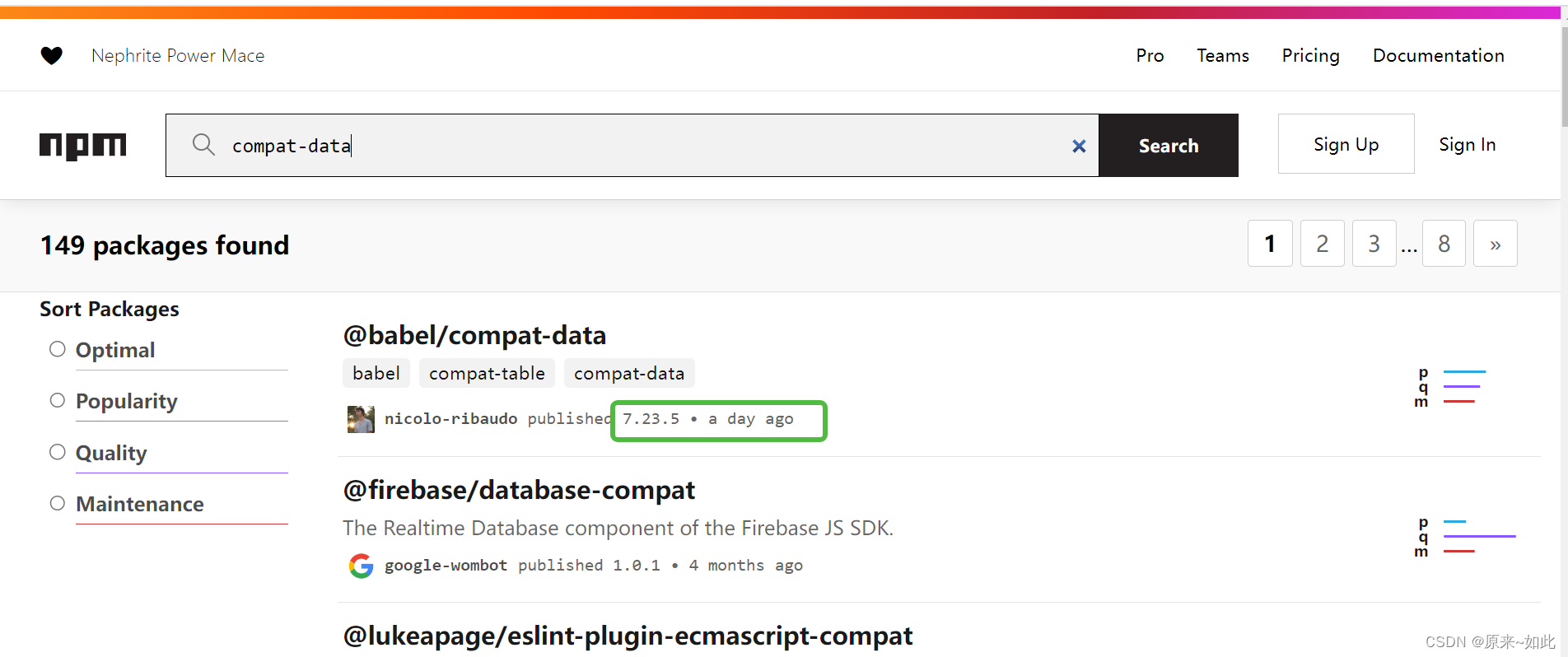
No matching version found for @babel/compat-data@^7.23.5 处理
npm ERR! notarget No matching version found for babel/compat-data^7.23.5 处理 报错信息 npm WARN ERESOLVE overriding peer dependency npm ERR! code ETARGET npm ERR! notarget No matching version found for babel/compat-data^7.23.5. npm ERR! notarget In most …...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...
