2023年亚太杯APMCM数学建模大赛A题水果采摘机器人的图像识别
2023年亚太杯APMCM数学建模大赛
A题 水果采摘机器人的图像识别
原题再现
中国是世界上最大的苹果生产国,年产量约3500万吨。同时,中国也是世界上最大的苹果出口国,世界上每两个苹果中就有一个是中国出口的,世界上超过六分之一的苹果是中国出口的。中国提出了“一带一路”倡议,这是建设未来共享的国际社会的重要支柱。由于这一举措,越南、孟加拉国、菲律宾、印度尼西亚等沿线国家已成为中国苹果的主要出口目的地。

苹果采摘主要依靠手工采摘。苹果成熟后,几天内就需要大量的采摘工人。但大多数当地农民在自己的果园里种植苹果。此外,农业工人的老龄化和年轻人离开村庄工作的现象导致了苹果采摘季节的劳动力短缺。为了解决这一问题,中国从2011年左右开始研究能够摘苹果的机器人,并取得了重大进展。
然而,由于果园环境与受控实验环境的差异,各种苹果采摘机器人在世界范围内的推广应用还不够理想。在复杂、非结构化的果园环境中,现有的机器人大多无法准确识别障碍物,如“树叶遮挡”、“树枝遮挡”、“水果遮挡”、“混合遮挡”等,如果直接采摘苹果而不根据实际场景做出准确判断,则损坏水果的风险很高,甚至对采摘手和机械臂造成伤害。这对收获效率和果实质量产生不利影响,导致更大的损失。此外,对不同采收果实的识别和分类也非常重要,如分类、加工、包装、运输等程序。然而,许多水果的颜色、形状和大小与苹果非常相似,这给苹果的采后识别带来了很大的困难。
本次竞赛的目的是通过分析和提取标记水果图像的特征,建立一个识别率高、速度快、准确度高的苹果图像识别模型,并对图像进行数据分析,如自动计算图像中苹果的数量、位置、成熟度,估计图像中苹果的质量等。具体任务如下:
问题1:数苹果
基于附件1中提供的已采收苹果图像数据集,提取图像特征,建立数学模型,统计每个图像中的苹果数,绘制附件1中所有苹果分布的直方图。
问题2:估计苹果的位置
根据附件1中提供的已收获苹果的图像数据集,以图像左下角为坐标原点,识别每个图像中苹果的位置,并绘制附件1中所有苹果几何坐标的二维散点图。
问题3:估计苹果的成熟状态
根据附件1提供的已采收苹果图像数据集,建立数学模型,计算每幅图像中苹果的成熟度,并绘制附件1中所有苹果成熟度分布的直方图。
问题4:估计苹果的质量
根据附件1中提供的已收获苹果的图像数据集,以图像左下角为坐标原点,计算每幅图像中苹果的二维面积,估计苹果的质量,并绘制附件1中所有苹果的质量分布直方图。
问题5:苹果的识别
基于附件2提供的采集水果图像数据集,提取图像特征,训练苹果识别模型,识别附件3中的苹果,并绘制附件3中所有苹果图像ID号的分布直方图。
import cv2
import torch
import torchvision
import numpy as np
from torchvision import transforms, utils
from matplotlib import pyplot as pltCLASS_NAMES = ['background', 'apple']
COLORS = np.random.uniform(0, 255, size=(len(CLASS_NAMES), 3))def load_model():model = torchvision.models.detection.fasterrcnn_resnet50_fpn(pretrained=True)model.eval()return modeldef load_and_process_image(image_path):image = cv2.imread(image_path)image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)transformed = transforms.Compose([transforms.ToTensor(),transforms.Resize((800, 800)),])image = transformed(image)return image.unsqueeze(0)model = load_model()import glob
import os
def visualize(image, boxes, labels, title,i):image = image.permute(1, 2, 0).numpy()fig = plt.figure(figsize=(8, 8))plt.imshow(image)ax = plt.gca()for i in range(len(boxes)):xmin, ymin, xmax, ymax = boxes[i]color = 'r'rect = plt.Rectangle((xmin, ymin), xmax - xmin, ymax - ymin, fill=False, edgecolor=color, linewidth=2)ax.add_patch(rect)text = '{:.2f}'.format(scores[i])plt.text(xmin, ymin-5, text, fontsize=8, bbox=dict(facecolor=color, alpha=0.5, pad=1), color='white')plt.axis('off')plt.title(title)plt.savefig('img/Q1_{}.png'.format(i),dpi=100)plt.show()# 循环读取图片
image_paths = sorted(glob.glob(os.path.join('Attachment/Attachment 1', '*.jpg')))
i=0
test = []
count_list = []
for image_path in image_paths:image = load_and_process_image(image_path)det_pred = model(image)boxes = det_pred[0]['boxes'].detach().numpy()scores = det_pred[0]['scores'].detach().numpy()labels = det_pred[0]['labels'].detach().numpy()threshold = 0.5idx = scores > thresholdboxes = boxes[idx]scores = scores[idx]labels = labels[idx]num_apples = len(boxes)count_list.append(num_apples)print('第{}张图片中苹果的数量为{}个'.format(i, num_apples))apple_locs = []for j in range(num_apples):xmin, ymin, xmax, ymax = boxes[j]apple_loc = (xmin, ymin, xmax, ymax)apple_locs.append(apple_loc)if i <= 3:visualize(image[0], boxes, labels, 'Image {}'.format(i),i)i+=1
# 绘制直方图
plt.hist(count_list, bins=range(max(count_list) + 2))
plt.xlabel("Apple count")
plt.ylabel("Image count")
plt.savefig('apple_number.png',dpi=300)
plt.show()
相关文章:

2023年亚太杯APMCM数学建模大赛A题水果采摘机器人的图像识别
2023年亚太杯APMCM数学建模大赛 A题 水果采摘机器人的图像识别 原题再现 中国是世界上最大的苹果生产国,年产量约3500万吨。同时,中国也是世界上最大的苹果出口国,世界上每两个苹果中就有一个是中国出口的,世界上超过六分之一的…...

mysql which is not in SELECT list; this is incompatible with DISTINCT解决方案
mysql报错Expression #1 of ORDER BY clause is not in SELECT list, references column ‘xxx’ which is not in SELECT list; this is incompatible with DISTINCT解决方案: 这是在 mysql5.7 版本,DISTINCT 与 order by 在一起用时则会报3065错误。因…...

linux /proc 文件系统
/proc系统是一个伪文件系统,它只存在内存当中,而不占用外存空间,以文件系统的方式为内核与进程提供通信的接口。 /proc目录下有很多以数字命名的目录,每个数字代表进程号PID它们是进程目录。系统中当前运行的每一个进程在/proc下都…...
java开发之个微群聊自动添加好友
请求URL: http://域名/addRoomMemberFriend 请求方式: POST 请求头Headers: Content-Type:application/jsonAuthorization:login接口返回 参数: 参数名必选类型说明wId是String登录实例标识chatRoom…...

Git .gitignore 忽略文件不生效解决方法
.gitignore 匹配规则 *.sample # 忽略所有 .sample 结尾的文件 !lib.sample # 但 lib.sample 除外 /TODO # 仅仅忽略项目根目录下的 TODO 文件,不包括 subdir/TODO build/ # 忽略 build/ 目录下的所有文件 doc/*.txt # 会…...

【Java】16. HashMap
16. HashMap public static String find3(String key) {Map<String, String> map Map.of("bright", "小明","white", "小白","black", "小黑");return map.get(key); }Map.of 用来创建不可变的 Map&#…...

KMP基础架构
前言 Kotlin可以用来开发全栈, 我们所熟悉的各个端几乎都支持(除了鸿蒙) 而我们要开发好KMP项目需要一个好的基础架构,这样不仅代码更清晰,而且能共享更多的代码 正文 我们可以先将KMP分为前端和服务端 它们两端也能共享一些代码,比如接口声明,bean类,基础工具类等 前端和…...

递归实现选择排序.
思路: 1.定位数组中的最大元素或最小元素 2.将其与第一个元素交换位置 3.接着将剩余未排序的元素中的最大值或最小值与第二个元素交换位置 4.以此类推,直到排序完成 示例: [ 8, 5, 1, 9, 3 ] //原始数组 [ 1, 5, 8, 9, 3 ] //3与8交换 [ 1, 3, 8, 9, 5 ] //3与5交换 [ 1,…...

Node.js【文件系统模块、路径模块 、连接 MySQL、nodemon、操作 MySQL】(三)-全面详解(学习总结---从入门到深化)
目录 Node.js 文件系统模块(二) Node.js 文件系统模块(三) Node.js 文件系统模块(四) Node.js 路径模块 Node.js 连接 MySQL Node.js nodemon Node.js 操作 MySQL Node.js 应用 Node.js 文件系统模块…...

公司的销售经理面临哪些压力和挑战?
公司的销售经理面临哪些压力和挑战? 作为公司的销售经理,通常会面临以下挑战和压力: 1. 销售目标难以达成。销售经理需要承担销售目标,这通常是一项艰巨的任务。他们需要制定销售策略,与客户建立联系,并确保…...

【Linux系统编程】如何创建进程(什么是fork函数?进程创建的原理是什么?)
目录 一、前言 二、 进程创建的初次了解(创建进程的原理) 三、什么是fork函数? 💦初识fork函数 💦fork函数的四个为什么? ⭐为什么fork()要给子进程返回0,给父进程返回子进程pidÿ…...
【opencv】计算机视觉基础知识
目录 前言 1、什么是计算机视觉 2、图片处理基础操作 2.1 图片处理:读入图像 2.2 图片处理:显示图像 2.3 图片处理:图像保存 3、图像处理入门基础 3.1 图像成像原理介绍 3.2 图像分类 3.2.1 二值图像 3.2.2灰度图像 3.2.3彩色图像…...
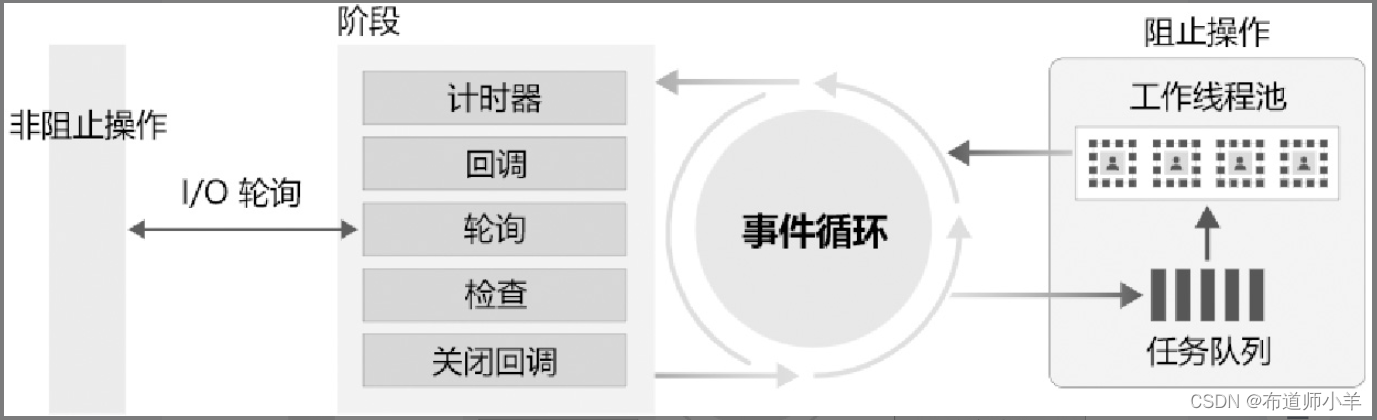
Node——Node.js简介
Node.js是一个基于Chrome V8引擎的JavaScript运行时环境,它能够让JavaScript脚本运行在服务端,这使得JavaScript成为与PHP、Python等服务端语言平起平坐的脚本语言。 1、认识Node.js Node.js是当今网站开发中非常流行的一种技术,它以简单易…...

小型洗衣机什么牌子好又便宜?性价比迷你洗衣机推荐
由于日常所穿的内衣裤由于各种原因,时间一久就很容易产生细菌,而且和其他大件的衣物一起混洗,很容易造成细菌的交叉感染,积攒起来洗就更不卫生了,留在内衣裤上的分泌物会继续滋生细菌,比如闷热的环境下念珠…...

INFINI Easysearch 与华为鲲鹏完成产品兼容互认证
何为华为鲲鹏认证 华为鲲鹏认证是华为云围绕鲲鹏云服务(含公有云、私有云、混合云、桌面云)推出的一项合作伙伴计划,旨在为构建持续发展、合作共赢的鲲鹏生态圈,通过整合华为的技术、品牌资源,与合作伙伴共享商机和利…...

将linux服务器 设置成 proxy.SOCKS5 服务器
gpt: 如果你想在 Linux 服务器上设置一个 SOCKS5 代理服务器,你可以使用一些现有的工具,比如 Shadowsocks、Dante、或者其他支持 SOCKS5 协议的软件。下面是一个使用 Dante 的简单示例: 1. **安装 Dante:** bash sudo apt-g…...
无mac电脑生成uniapp云打包私钥证书的攻略
uniapp顾名思义是一个跨平台的开发工具,大部分uniapp的开发者,其实并没有mac电脑来开发,但是生成ios的证书,官网的教程却是需要mac电脑的,那么有没有办法无需mac电脑即可生成uniapp云打包的私钥证书呢? 下…...

py 启动默认浏览器
要在Python中启动默认浏览器,可以使用第三方库如webbrowser或pyperclip,也可以使用操作系统特定的命令行调用。以下是几个不同的方法: 使用webbrowser库: import webbrowser webbrowser.open("http://example.com")这…...

scala可变参数列表使用
在Scala中,可以使用可变参数列表(varargs)来定义一个函数,以接受可变数量的参数。示例如下: def printArgs(args: String*): Unit {args.foreach(println) }// 使用可变参数列表 printArgs("Hello", "…...

经验分享:JMeter控制RPS
一、前言 RPS (Request Per Second)一般用来衡量服务端的吞吐量,相比于并发模式,更适合用来摸底服务端的性能。我们可以通过使用 JMeter 的常数吞吐量定时器来限制每个线程的RPS。对于RPS,我们可以把他理解为我们的TPS,我们就…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...
基础)
6个月Python学习计划 Day 16 - 面向对象编程(OOP)基础
第三周 Day 3 🎯 今日目标 理解类(class)和对象(object)的关系学会定义类的属性、方法和构造函数(init)掌握对象的创建与使用初识封装、继承和多态的基本概念(预告) &a…...

从物理机到云原生:全面解析计算虚拟化技术的演进与应用
前言:我的虚拟化技术探索之旅 我最早接触"虚拟机"的概念是从Java开始的——JVM(Java Virtual Machine)让"一次编写,到处运行"成为可能。这个软件层面的虚拟化让我着迷,但直到后来接触VMware和Doc…...
