【数据库】数据库并发控制的冲突检测,冲突可串行化的调度,保障事务的特性
冲突可串行化
专栏内容:
- 手写数据库toadb
本专栏主要介绍如何从零开发,开发的步骤,以及开发过程中的涉及的原理,遇到的问题等,让大家能跟上并且可以一起开发,让每个需要的人成为参与者。
本专栏会定期更新,对应的代码也会定期更新,每个阶段的代码会打上tag,方便阶段学习。
开源贡献:
- toadb开源库
个人主页:我的主页
管理社区:开源数据库
座右铭:天行健,君子以自强不息;地势坤,君子以厚德载物.
文章目录
- 冲突可串行化
- 前言
- 概述
- 冲突
- 冲突的概念
- 冲突的发生条件
- 冲突可串行化
- 优先图检测方法
- 总结
- 结尾

前言
随着信息技术的飞速发展,数据已经渗透到各个领域,成为现代社会最重要的资产之一。在这个大数据时代,数据库理论在数据管理、存储和处理中发挥着至关重要的作用。然而,很多读者可能对数据库理论感到困惑,不知道如何选择合适的数据库,如何设计有效的数据库结构,以及如何处理和管理大量的数据。因此,本专栏旨在为读者提供一套全面、深入的数据库理论指南,帮助他们更好地理解和应用数据库技术。
数据库理论是研究如何有效地管理、存储和检索数据的学科。在现代信息化社会中,数据量呈指数级增长,如何高效地处理和管理这些数据成为一个重要的问题。同时,随着云计算、物联网、大数据等新兴技术的不断发展,数据库理论的重要性日益凸显。
因此,本专栏的分享希望可以提高大家对数据库理论的认识和理解,对于感兴趣的朋友带来帮助。
概述
商用数据库管理系中的调度器通常强制执行被称为“冲突可串行化”的条件,它比前一篇博文中分享的可串行化的一般要强,它是基于冲突这一概念。
我们通常执行的很多并发事务,都会发生冲突,本文就来分享一下突冲的原因,以及如何检测冲突发生,如何做到冲突可串行化。
冲突
首先我们先来了解一下冲突是什么?
冲突的概念
冲突,即调度中一对连续的动作,它们满足,如果它们的顺序发生交换,那么它们涉及的事务至少有一个的行为会改变。
冲突的发生条件
一般什么情况下会发生冲突呢?
数据库的操作可以分为写和读两种,我们看一下两个事务,分别有一个操作时,什么情况下为会产生冲突。
- 当两个事务对同一数据库元素读时,先后顺序交换,并不发生结果的改变,不会冲突;
- 当两个事务操作同一个数据元素时,有一个读,一个写时,先后顺序交换,读操作的事务的结果就会不一样,这时就会产生冲突;
- 当两个事务操作同一个数据元素时,两个事务都进行写操作,先后顺序交换,两个事务的结果都不会一样;
- 当两个事务操作不同数据库元素时,不管是读还是写,顺序交换,结果都不会受影响,所以不会产生冲突;
从上面例子可以得到这样一个结论:
- 不同事务操作同一个数据库元素;
- 操作中至少有一个是写操作;
那么我们将一个执行序列进行调度,进行任意非冲突的可串行化调度,目标是将这一序列转化为可串行化,如果能达到这一点,那么它最初调度是可串行化的调度,因为在做每一个非冲突可串行化调度时,初始状态一样,对数据库的影响在不同序列下是一样的。
冲突可串行化
-
如果对于并发执行的序列进行一系列相邻动作的非冲突交换,能转换为另一个,这两个调度可以称为冲突等价的。
-
如果一个冲突调度等价于一个可串行化调度,那么可以称这个调度为冲突可串行化;
当然冲突可串行化是可串行化的充分非必要条件,
优先图检测方法
通过上面的冲突发生条件分析,说明事务的语义会影响串行化,但是对于调度器来说,它不会深入到事务执行的细节,但是调度器能够看来自事务的读写请求,以及那些数据元素发生了改变,这样它可以通过数据元组的访问来识别冲突。
在一个调度执行序列中,可以确定冲突动作对应的事务的先后顺序,如何事务先后顺序在不同冲突动作上,呈现出不同的顺序,那么我们认为是冲突不可串行化的。
那这一特点通过优先图就可以体现出来。
T1->T2->T3
如果是这样一个图,那么就是冲突可串行化的。
T1->T2->T3->T2
如果是这样一个图,T2与T3之间存在了一个环,那么就是冲突不可串行化的。
总结
在数据库并发事务情况下,冲突是不可避免的,通过优先图的方法来检测冲突,使得调度器能够找到一种冲突可串行化的调度方案。
这是一个简单的C语言程序,它使用了状态模式来输出"Hello, world!":
#include <stdio.h>
#include <stdlib.h>// 定义状态结构体
typedef struct State State;
struct State {void (*printMessage)(void);
};// 定义转换函数
void printHello(void) {printf("Hello, world!\n");
}// 定义初始状态
State initialState = { .printMessage = printHello };// 定义状态转换函数
void transition(State *state) {switch (*state) {case 'H':(*state).printMessage = printHello;break;default:printf("Invalid state\n");break;}
}int main() {State state = initialState;transition(&state);return 0;
}
这个程序定义了一个状态结构体,其中有一个函数指针用于指向打印消息的函数。然后定义了一个初始状态,该状态中的函数指针指向printHello函数。transition函数接受一个指向状态的指针,并根据当前状态来改变它指向的函数。在main函数中,我们首先设置初始状态,然后调用transition函数来改变状态。
结尾
非常感谢大家的支持,在浏览的同时别忘了留下您宝贵的评论,如果觉得值得鼓励,请点赞,收藏,我会更加努力!
作者邮箱:study@senllang.onaliyun.com
如有错误或者疏漏欢迎指出,互相学习。
相关文章:

【数据库】数据库并发控制的冲突检测,冲突可串行化的调度,保障事务的特性
冲突可串行化 专栏内容: 手写数据库toadb 本专栏主要介绍如何从零开发,开发的步骤,以及开发过程中的涉及的原理,遇到的问题等,让大家能跟上并且可以一起开发,让每个需要的人成为参与者。 本专栏会定期更新…...
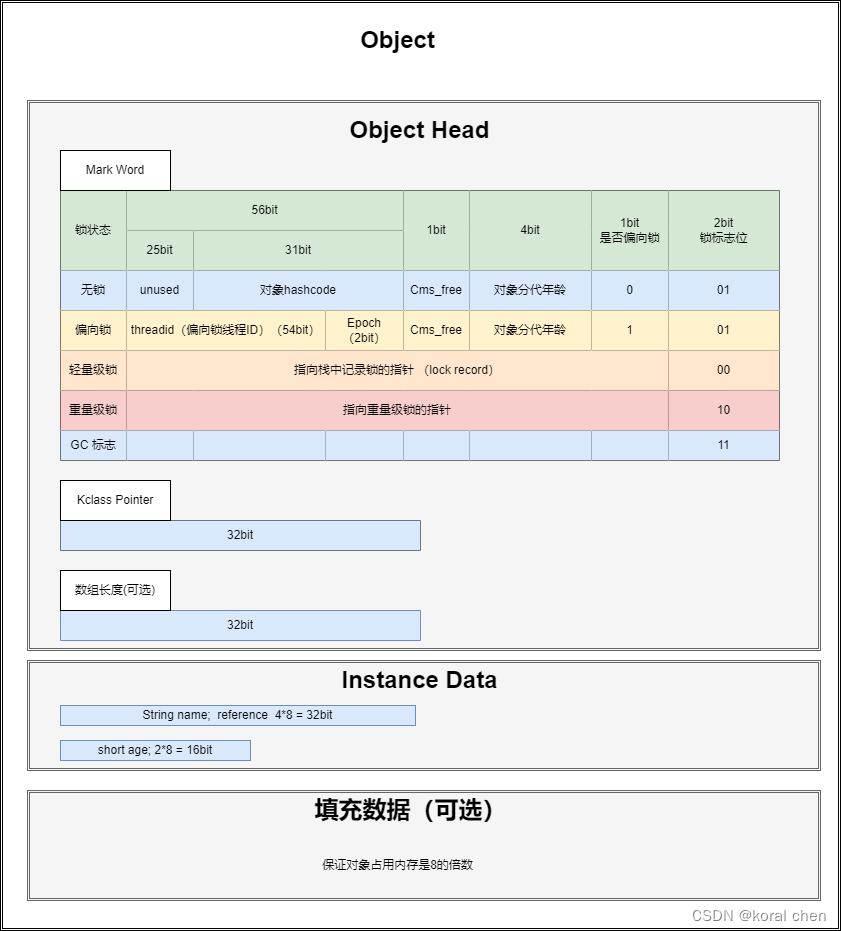
java 对象大小计算
说明: 对于64位机:一个对象由三部分组成 对象头(object header) mark word :64bitkclass pointer :32bit(默认使用指针压缩),如果取消指针压缩( XX:-UseCompressedOops),则占用64bit数组长度:数…...
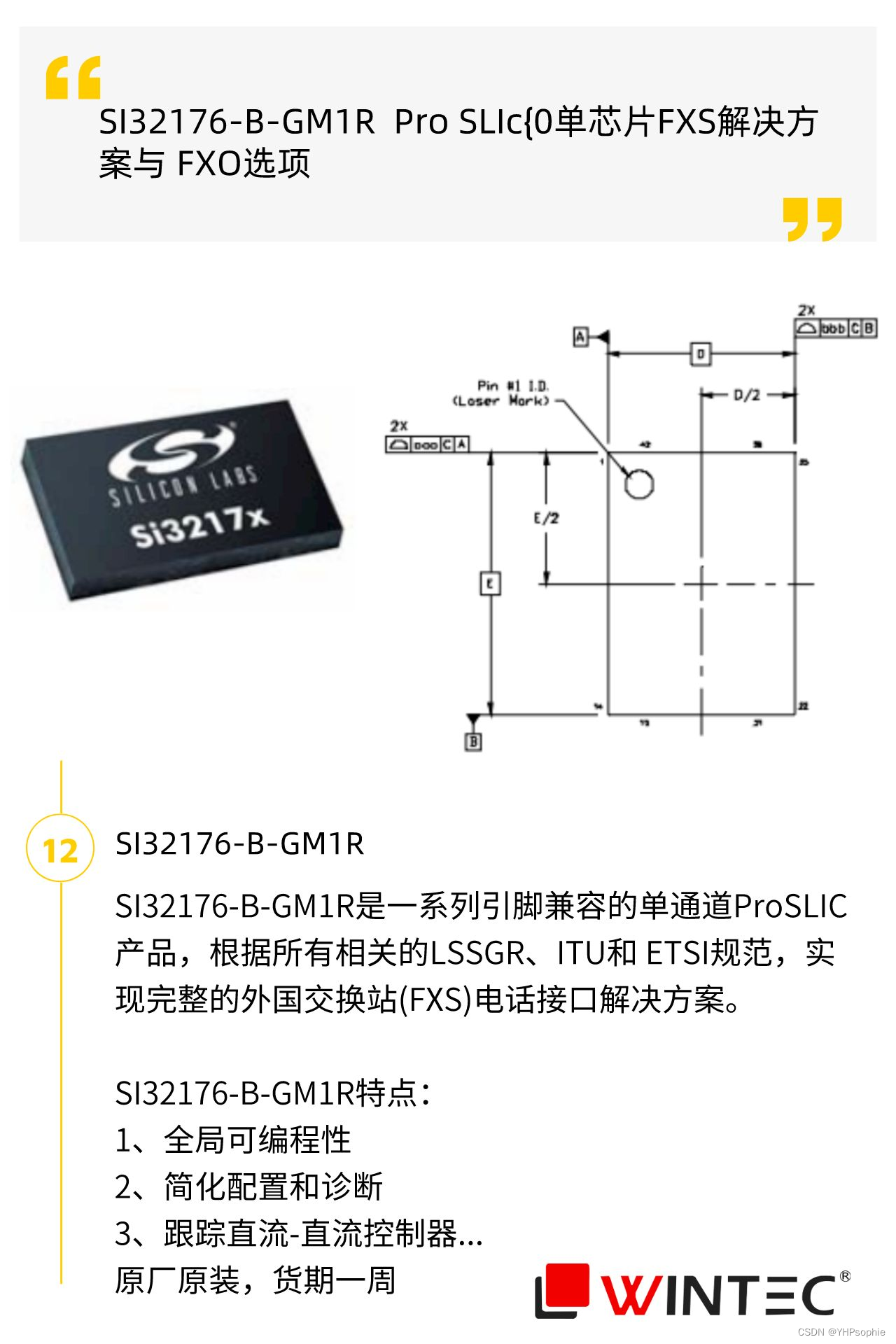
12个国外电子元器件基本参数(下)
DAC8162SDSCR TI DAC088S085CISQNOPB TI TL4050C41QDBZR TI NE3516S02-T1D-A RENESAS TECHNOLOGY MXL862-AL-R MAXLINEAR SI32176-B-GM1R SILICON LAB...

Docker容器中的OpenCV:轻松构建可移植的计算机视觉环境
前言 「作者主页」:雪碧有白泡泡 「个人网站」:雪碧的个人网站 构建可移植的计算机视觉环境 文章目录 前言引言简介:目的和重要性: 深入理解Docker和OpenCVDocker的基本概念和优势:OpenCV简介和应用领域:…...

SSH基础和高级用法
SSH基础和高级用法 SSH(Secure Shell)是一种安全协议,用于在不安全的网络上提供安全的远程登录和数据传输。以下是一些SSH的用法和高级用法: 基本用法: 远程登录:使用ssh命令可以实现在本地计算机上远程…...

算法通关第十三关-青铜挑战数学基础问题
数组元素积的符号 描述 : 已知函数 signFunc(x) 将会根据 x 的正负返回特定值: 如果 x 是正数,返回 1 。如果 x 是负数,返回 -1 。如果 x 是等于 0 ,返回 0 。 给你一个整数数组 nums 。令 product 为数组 nums 中所有元素值的…...

如何使用 Freepik 的 Pikaso 工具来画图
Freepik 是一个提供高质量的照片、矢量图像、插图以及 PSD 文件素材的网站https://www.freepik.com/您可以在这里找到各种风格和主题的素材,用于您的创意项目。Freepik 还提供了一个名为 Pikaso 的在线画图工具,让您可以轻松地创建和编辑您自己的图像&am…...

一个没正常处理tcp对端关闭的bug
最近使用自研的http client时发现一个问题,对端在发送响应数据之后立即调用close关闭了连接,我这没有调用到响应的回调,而是调用到了连接关闭的回调。对端延迟一会再关闭连接就没问题,用curl去访问也是正常的。经过排查是没有正确…...

什么是JDK
JDK是Java的开发工具,全称为Java Development Kit,包含Java运行环境,Java工具,Java基础类库三大部分。 Java运行环境 Java运行环境,也就是JRE,全称为Java Runtime Environment ,其中包含JVM&…...
)
积分表二(高等数学同济版中所有的积分公式)
文章目录 含有 x − a x a \sqrt{\pm \frac{x-a}{xa}} xax−a 或者 ( x − a ) ( b − x ) \sqrt{(x-a)(b-x)} (x−a)(b−x) 的积分含有三角函数函数的积分含有反三角函数的积分 (其中 a > 0 a>0 a>0)含有指数函数的积分含有对数函数的积分含有双曲函数的…...

Golang数据类型(数字型)
Go数据类型(数字型) Go中数字型数据类型大致分为整数(integer)、浮点数(floating point )和复数(Complex)三种 整数重要概念 整数在Go和Python中有较大区别,主要体现在…...
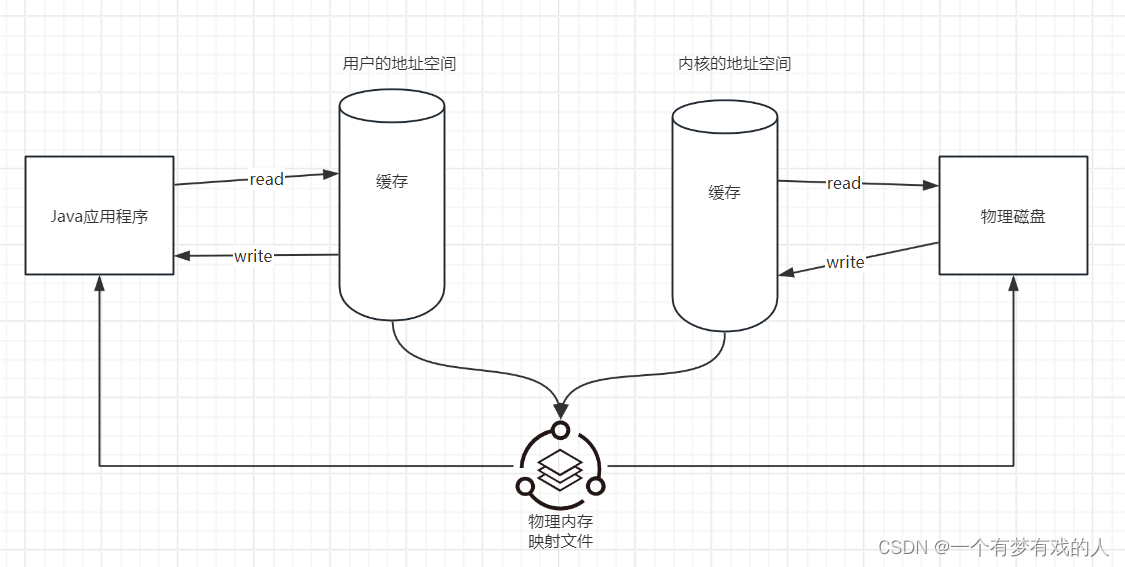
【JVM系列】- 穿插·对象的实例化与直接内存
对象的实例化与直接内存 😄生命不息,写作不止 🔥 继续踏上学习之路,学之分享笔记 👊 总有一天我也能像各位大佬一样 🌝分享学习心得,欢迎指正,大家一起学习成长! 文章目录…...
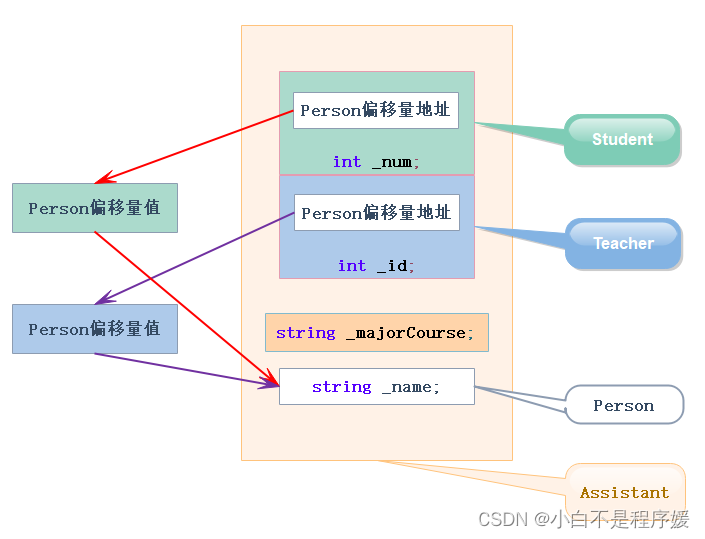
【C++干货铺】继承 | 多继承 | 虚继承
个人主页点击直达:小白不是程序媛 C系列专栏:C干货铺 代码仓库:Gitee 目录 继承的概念及定义 继承的概念 继承的定义 继承基类成员访问方式的变化 基类和派生类的赋值转化 继承中的作用域 派生类的默认成员函数 构造函数 拷贝构造…...

【ARM CoreLink 系列 8.1 -- SMMU 详细介绍-STE Entry 详细介绍 1】
请阅读【ARM CoreLink 文章专栏导读】 上篇文章:【ARM CoreLink 系列 8 – SMMU 详细介绍-上半部】 文章目录 ARM SMMU STE ENTRY1.1 STE ENTRYWORD[0]1.1.1 S1ContexPtr1.1.2 S1Fmt1.1.3 Config1.1.4 V(Valid)1.2 STE ENTRY WORD[1]1.2.1 S1CDMax1.2.2 S1ContextPtr1.3 STE E…...

高防CDN与WAF防火墙的协同防护:构筑网络安全堡垒
随着互联网的不断发展,网络安全威胁也日益增多,而网站作为企业在数字领域的门户,面临的风险更加复杂多样。在构筑网络安全堡垒的过程中,高防CDN(Content Delivery Network)与WAF(Web Applicatio…...

golang strings包的基本操作
文章目录 golang 的字符串函数EqualFoldHasPrefixHasSuffixContainsContainsRuneContainsAnyCountIndexIndexByteIndexRuneIndexAnyIndexFuncLastIndexLastIndexAnyLastIndexFuncTitleToLowerToLowerSpecialToUpperToUpperSpecialToTitleToTitleSpecialRepeatReplaceMapTrimTri…...

高效解决在本地打开可视化服务器端的tensorboard
文章目录 问题解决方案 问题 由于连着远程服务器构建模型,但是想在本地可视化却做不到,不要想当然天真的以为CTRLC点击链接http://localhost:6006就真能在本地打开tensorboard。你电脑都没连接服务器,只是pycharm连上了而已 解决方案 你需要…...

Spring Boot Actuator 2.2.5 基本使用
1. pom文件 ,添加 Actuator 依赖 <dependency> <groupId>org.springframework.boot</groupId> <artifactId>spring-boot-starter-actuator</artifactId> </dependency> 2.application.properties 文件中添加以下配置 …...

字符串相似度匹配算法_莱茵斯坦距离算法
package day0330;public class LevenshteinDistanceUtil {public static void main(String[] args) {String a "WN64 F98";String b "WN64 F98 ";System.out.println("相似度:" getSimilarityRatio(a, b));}/*** 获取两字符串的相似度* * par…...

【EI会议征稿】第九届电气、电子和计算机工程研究国际学术研讨会 (ISAEECE 2024)
第九届电气、电子和计算机工程研究国际学术研讨会 (ISAEECE 2024) 2024 9th International Symposium on Advances in Electrical, Electronics and Computer Engineering 第九届电气、电子和计算机工程研究国际学术研讨会(ISAEECE 2024)将于2024年3月1-5日在南…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

门静脉高压——表现
一、门静脉高压表现 00:01 1. 门静脉构成 00:13 组成结构:由肠系膜上静脉和脾静脉汇合构成,是肝脏血液供应的主要来源。淤血后果:门静脉淤血会同时导致脾静脉和肠系膜上静脉淤血,引发后续系列症状。 2. 脾大和脾功能亢进 00:46 …...
