算法通关第十三关-青铜挑战数学基础问题
数组元素积的符号
描述 :
已知函数 signFunc(x) 将会根据 x 的正负返回特定值:
- 如果
x是正数,返回1。 - 如果
x是负数,返回-1。 - 如果
x是等于0,返回0。
给你一个整数数组 nums 。令 product 为数组 nums 中所有元素值的乘积。
题目 :
LeetCode 1822.数组元素积的符号 :
1822. 数组元素积的符号

分析 ;
我们只需要看有多少个负数,最后乘积的符号就能够判断 :
解析 :
class Solution {public int arraySign(int[] nums) {int count = 1;for(int i = 0;i < nums.length;i++){if(nums[i] == 0){return 0;}else if(nums[i] < 0){count = -count;}}return count;}
}阶乘0的个数
描述 :
给定一个整数 n ,返回 n! 结果中尾随零的数量。
题目 :
LeetCode 阶乘尾零 :
面试题 16.05. 阶乘尾数
172. 阶乘后的零

分析 :
这个题如果硬算,一定会超时,其实我们可以统计有多少个0,实际上是统计 2和5一起出现多少对,不过因为 2 出现的次数一定大于 5 出现的次数,因此我们只需要检查 5 出现的次数就好了,那么在统计过程中,我们只需要统计 5、10、15、25、 ...5^n 这样5 的整数倍项就好了,最后累加起来,就是多少0。代码就是:
解析 :
class Solution {public int trailingZeroes(int n) {int count = 0;for(long num = 5; n / num > 0;num *= 5){count += n / num;}return count;}
}整数反转
描述 :
给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果。
如果反转后整数超过 32 位的有符号整数的范围 [−231, 231 − 1] ,就返回 0。
假设环境不允许存储 64 位整数(有符号或无符号)。
题目 :
LeetCode 7.整数反转 :
7. 整数反转

分析 :
力扣官方题解
解析 :
class Solution {public int reverse(int x) {int rev = 0;while (x != 0) {if (rev < Integer.MIN_VALUE / 10 || rev > Integer.MAX_VALUE / 10) {return 0;}int digit = x % 10;x /= 10;rev = rev * 10 + digit;}return rev;}
}回文数
描述 :
给你一个整数 x ,如果 x 是一个回文整数,返回 true ;否则,返回 false 。
回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。
- 例如,
121是回文,而123不是。
题目 :
LeetCode 9.回文数 :
9. 回文数

分析 :
为了避免数字反转可能导致的溢出问题,只反转 int 数字的一半
毕竟,如果该数字是回文,其后半部分反转后应该与原始数字的前半部分相同。
解析 :
class Solution {public boolean isPalindrome(int x) {if(x < 0 || (x % 10 == 0 && x != 0)){return false;}int res = 0;while(x > res){res = res * 10 + x % 10;x /= 10;}return x == res || x == res / 10;}
}七进制数
描述 :
给定一个整数 num,将其转化为 7 进制,并以字符串形式输出。
题目 :
LeetCode 504. 七进制数 :
504. 七进制数

分析 :
我们先通过二进制想一下7进制数的变化特征。在二进制中,先是0,然后是1,而2就是10(2),3就是11(2),4就是(100)。
同样在7进制中,计数应该是这样的 :
100 / 7=14 余 2
14 / 7=2 余0
2 / 7=0 余2
向遍历每次的余数,依次是 2、0、2,因此十进制数 100 转成七进制数是202 。如果num<0,则先对num 取绝对值,然后再转换即可。使用代码同样可以实现该过程,需要注意的是如果单纯按照整数来处理会非常麻烦,既然题目说以字符串形式返回,那我们干脆直接用字符串类,
解析 :
class Solution {public String convertToBase7(int num) {StringBuilder sb = new StringBuilder();int flag = 0;if(num < 0){num *= -1;flag = 1;}do{sb.append(num % 7 + "");num /= 7;}while(num > 0);if(flag == 1){sb.append("-");}return sb.reverse().toString();}
}这期就到这里 , 下期见!
相关文章:

算法通关第十三关-青铜挑战数学基础问题
数组元素积的符号 描述 : 已知函数 signFunc(x) 将会根据 x 的正负返回特定值: 如果 x 是正数,返回 1 。如果 x 是负数,返回 -1 。如果 x 是等于 0 ,返回 0 。 给你一个整数数组 nums 。令 product 为数组 nums 中所有元素值的…...

如何使用 Freepik 的 Pikaso 工具来画图
Freepik 是一个提供高质量的照片、矢量图像、插图以及 PSD 文件素材的网站https://www.freepik.com/您可以在这里找到各种风格和主题的素材,用于您的创意项目。Freepik 还提供了一个名为 Pikaso 的在线画图工具,让您可以轻松地创建和编辑您自己的图像&am…...

一个没正常处理tcp对端关闭的bug
最近使用自研的http client时发现一个问题,对端在发送响应数据之后立即调用close关闭了连接,我这没有调用到响应的回调,而是调用到了连接关闭的回调。对端延迟一会再关闭连接就没问题,用curl去访问也是正常的。经过排查是没有正确…...

什么是JDK
JDK是Java的开发工具,全称为Java Development Kit,包含Java运行环境,Java工具,Java基础类库三大部分。 Java运行环境 Java运行环境,也就是JRE,全称为Java Runtime Environment ,其中包含JVM&…...
)
积分表二(高等数学同济版中所有的积分公式)
文章目录 含有 x − a x a \sqrt{\pm \frac{x-a}{xa}} xax−a 或者 ( x − a ) ( b − x ) \sqrt{(x-a)(b-x)} (x−a)(b−x) 的积分含有三角函数函数的积分含有反三角函数的积分 (其中 a > 0 a>0 a>0)含有指数函数的积分含有对数函数的积分含有双曲函数的…...

Golang数据类型(数字型)
Go数据类型(数字型) Go中数字型数据类型大致分为整数(integer)、浮点数(floating point )和复数(Complex)三种 整数重要概念 整数在Go和Python中有较大区别,主要体现在…...
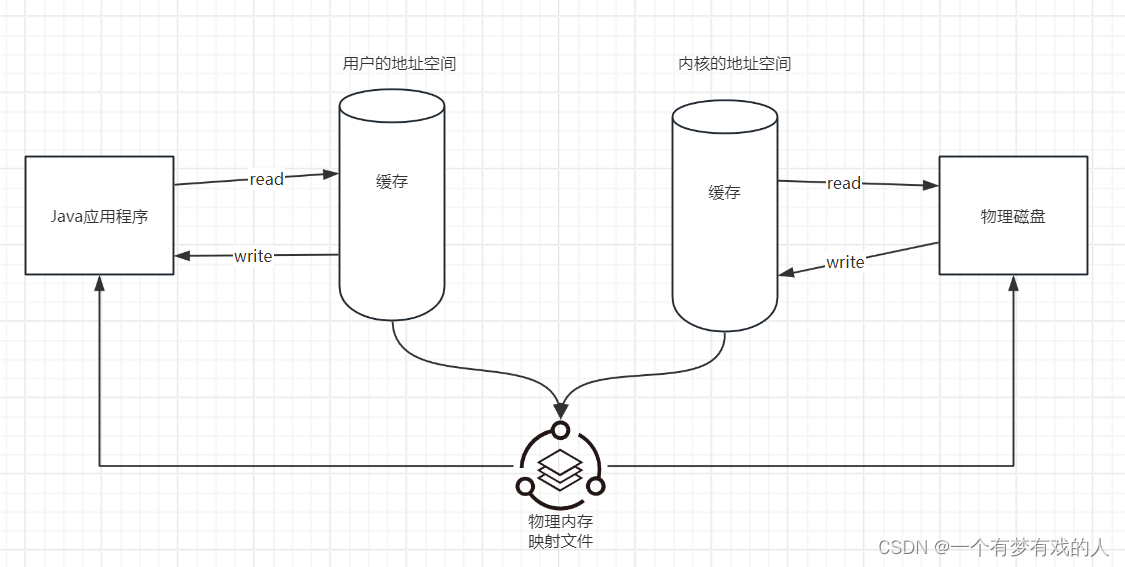
【JVM系列】- 穿插·对象的实例化与直接内存
对象的实例化与直接内存 😄生命不息,写作不止 🔥 继续踏上学习之路,学之分享笔记 👊 总有一天我也能像各位大佬一样 🌝分享学习心得,欢迎指正,大家一起学习成长! 文章目录…...
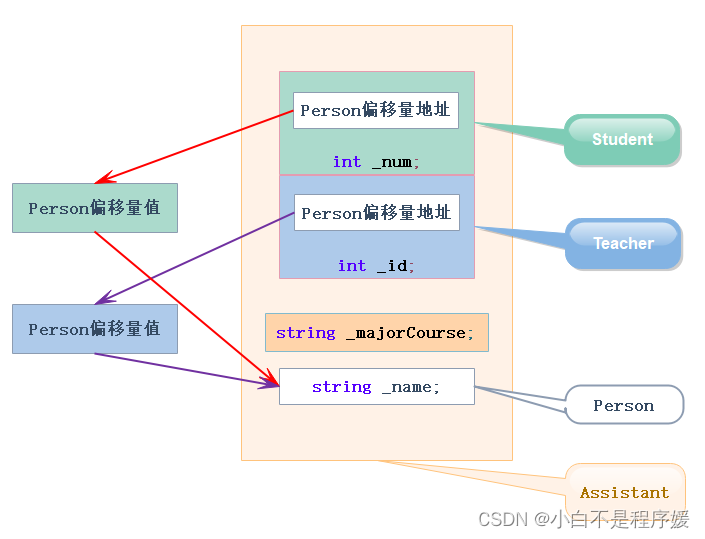
【C++干货铺】继承 | 多继承 | 虚继承
个人主页点击直达:小白不是程序媛 C系列专栏:C干货铺 代码仓库:Gitee 目录 继承的概念及定义 继承的概念 继承的定义 继承基类成员访问方式的变化 基类和派生类的赋值转化 继承中的作用域 派生类的默认成员函数 构造函数 拷贝构造…...

【ARM CoreLink 系列 8.1 -- SMMU 详细介绍-STE Entry 详细介绍 1】
请阅读【ARM CoreLink 文章专栏导读】 上篇文章:【ARM CoreLink 系列 8 – SMMU 详细介绍-上半部】 文章目录 ARM SMMU STE ENTRY1.1 STE ENTRYWORD[0]1.1.1 S1ContexPtr1.1.2 S1Fmt1.1.3 Config1.1.4 V(Valid)1.2 STE ENTRY WORD[1]1.2.1 S1CDMax1.2.2 S1ContextPtr1.3 STE E…...

高防CDN与WAF防火墙的协同防护:构筑网络安全堡垒
随着互联网的不断发展,网络安全威胁也日益增多,而网站作为企业在数字领域的门户,面临的风险更加复杂多样。在构筑网络安全堡垒的过程中,高防CDN(Content Delivery Network)与WAF(Web Applicatio…...

golang strings包的基本操作
文章目录 golang 的字符串函数EqualFoldHasPrefixHasSuffixContainsContainsRuneContainsAnyCountIndexIndexByteIndexRuneIndexAnyIndexFuncLastIndexLastIndexAnyLastIndexFuncTitleToLowerToLowerSpecialToUpperToUpperSpecialToTitleToTitleSpecialRepeatReplaceMapTrimTri…...

高效解决在本地打开可视化服务器端的tensorboard
文章目录 问题解决方案 问题 由于连着远程服务器构建模型,但是想在本地可视化却做不到,不要想当然天真的以为CTRLC点击链接http://localhost:6006就真能在本地打开tensorboard。你电脑都没连接服务器,只是pycharm连上了而已 解决方案 你需要…...

Spring Boot Actuator 2.2.5 基本使用
1. pom文件 ,添加 Actuator 依赖 <dependency> <groupId>org.springframework.boot</groupId> <artifactId>spring-boot-starter-actuator</artifactId> </dependency> 2.application.properties 文件中添加以下配置 …...

字符串相似度匹配算法_莱茵斯坦距离算法
package day0330;public class LevenshteinDistanceUtil {public static void main(String[] args) {String a "WN64 F98";String b "WN64 F98 ";System.out.println("相似度:" getSimilarityRatio(a, b));}/*** 获取两字符串的相似度* * par…...

【EI会议征稿】第九届电气、电子和计算机工程研究国际学术研讨会 (ISAEECE 2024)
第九届电气、电子和计算机工程研究国际学术研讨会 (ISAEECE 2024) 2024 9th International Symposium on Advances in Electrical, Electronics and Computer Engineering 第九届电气、电子和计算机工程研究国际学术研讨会(ISAEECE 2024)将于2024年3月1-5日在南…...
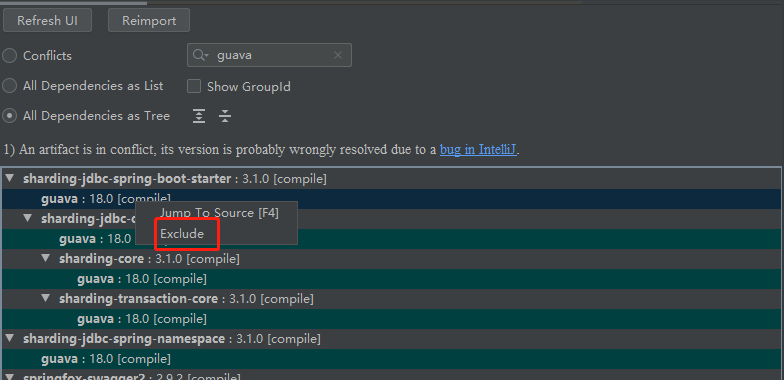
Maven Helper插件——实现一键Maven依赖冲突问题
总结/朱季谦 业余在一个SpringBoot项目集成Swagger2时,启动过程一直出现以下报错信息—— An attempt was made to call a method that does not exist. The attempt was made from the following location: springfox.documentation.schema.DefaultModelDepe…...
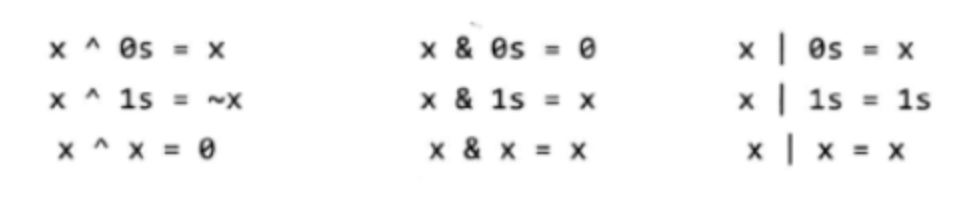
理解位运算的规则
关卡名 理解位运算的规则 我会了✔️ 内容 1.理解位运算的基本规则 ✔️ 2.理解移位的原理以及与乘除的关系 ✔️ 3.掌握位运算的常用技巧 ✔️ 在学习位操作之前,我们先明确数据在计算机中怎么表示的。我们明确原码、反码和补码的概念和表示方法,之…...
Android Bitmap 使用Vukan、RenderEffect、GLSL实现模糊
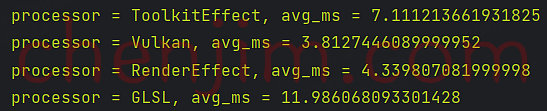
文章目录 Android Bitmap 使用Vukan、RenderEffect、GLSL实现模糊使用 RenderEffect 模糊使用 Vukan 模糊使用 GLSL 模糊RS、Vukan、RenderEffect、GLSL 效率对比 Android Bitmap 使用Vukan、RenderEffect、GLSL实现模糊 本文首发地址 https://blog.csdn.net/CSqingchen/articl…...

Vue H5页面长按保存为图片
安装依赖:npm install html2canvas -d <template><div class"index"><div id"captureId" class"capture" v-show"firstFlag"><ul><li>1</li><li>2</li><li>3<…...
【Web】UUCTF 2022 新生赛 个人复现
目录 ①websign ②ez_rce ③ez_upload ④ez_unser ⑤ezsql ⑥ezpop ⑦funmd5 ⑧phonecode ⑨ezrce ①websign 右键打不开,直接抓包发包看源码 ②ez_rce “反引号” 在PHP中会被当作SHELL命令执行 ?codeprintf(l\s /); ?codeprintf(ta\c /ffffffffffl…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

【VLNs篇】07:NavRL—在动态环境中学习安全飞行
项目内容论文标题NavRL: 在动态环境中学习安全飞行 (NavRL: Learning Safe Flight in Dynamic Environments)核心问题解决无人机在包含静态和动态障碍物的复杂环境中进行安全、高效自主导航的挑战,克服传统方法和现有强化学习方法的局限性。核心算法基于近端策略优化…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

第八部分:阶段项目 6:构建 React 前端应用
现在,是时候将你学到的 React 基础知识付诸实践,构建一个简单的前端应用来模拟与后端 API 的交互了。在这个阶段,你可以先使用模拟数据,或者如果你的后端 API(阶段项目 5)已经搭建好,可以直接连…...

Pydantic + Function Calling的结合
1、Pydantic Pydantic 是一个 Python 库,用于数据验证和设置管理,通过 Python 类型注解强制执行数据类型。它广泛用于 API 开发(如 FastAPI)、配置管理和数据解析,核心功能包括: 数据验证:通过…...

Python常用模块:time、os、shutil与flask初探
一、Flask初探 & PyCharm终端配置 目的: 快速搭建小型Web服务器以提供数据。 工具: 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask: 建议: 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装,避免频繁切换。 PyCharm Terminal 配置建议: 打开 Py…...

【iOS】 Block再学习
iOS Block再学习 文章目录 iOS Block再学习前言Block的三种类型__ NSGlobalBlock____ NSMallocBlock____ NSStackBlock__小结 Block底层分析Block的结构捕获自由变量捕获全局(静态)变量捕获静态变量__block修饰符forwarding指针 Block的copy时机block作为函数返回值将block赋给…...
