理解位运算的规则
| 关卡名 | 理解位运算的规则 | 我会了✔️ |
| 内容 | 1.理解位运算的基本规则 | ✔️ |
| 2.理解移位的原理以及与乘除的关系 | ✔️ | |
| 3.掌握位运算的常用技巧 | ✔️ |
在学习位操作之前,我们先明确数据在计算机中怎么表示的。我们明确原码、反码和补码的概念和表示方法,之后介绍位运算相关的问题。
1 数字在计算机中的表示
机器数 一个数在计算机中的二进制表示形式,叫做这个数的机器数。机器数是带符号的,在计算机用一个数的最高位存放符号,正数为0,负数为1。比如,十进制中的数 +3 ,计算机字长为8位,转换成二进制就是00000011。如果是 -3 ,就是 10000011 。这里的 00000011 和 10000011 就是机器数。
真值 因为机器数第一位是符号位,所以机器数的形式值就不等于真正的数值。例如上面的有符号数 10000011,其最高位1代表负,其真正数值是 -3 而不是形式值131(10000011转换成十进制等于131)。所以,为了好区别,将带符号位的机器数对应的真正数值称为机器数的真值。例:0000 0001的真值 = +000 0001 = +1,1000 0001的真值 = –000 0001 = –1。
计算机对机器数的表示进一步细化:原码, 反码, 补码。
原码 就是符号位加上真值的绝对值,即用第一位表示符号,其余位表示值, 比如如果是8位二进制:
[+1]原 = 0000 0001
[-1]原 = 1000 0001
第一位是符号位,因为第一位是符号位,所以8位二进制数的取值范围就是:
[1111 1111 , 0111 1111],也即 [-127 , 127]
反码 的表示方法是:正数的反码是其本身,而负数的反码是在其原码的基础上,符号位不变,其余各个位取反。例如:
[+1] = [00000001]原 = [00000001]反
[-1] = [10000001]原 = [11111110]反
可见如果一个反码表示的是负数,人脑无法直观的看出来它的数值,通常要将其转换成原码再计算。
在应用中,因为补码 能保持加和减运算的统一,因此应用更广,其表示方法是:
- 正数的补码就是其本身;
- 负数的补码是在其原码的基础上,符号位不变,其余各位取反,最后+1(即在反码的基础上+1)。
[+1] = [00000001]原 = [00000001]反 = [00000001]补
[-1] = [10000001]原 = [11111110]反 = [11111111]补
对于负数, 补码表示方式也是人脑无法直观看出其数值的,通常也需要转换成原码在计算其数值。
拓展 为何会有原码,反码和补码
既然原码就能表示数据,那为什么实际软件中更多使用的是补码呢?接下来我们就看一看。
现在我们知道了计算机可以有三种编码方式表示一个数,对于正数因为三种编码方式的结果都相同:
[+1] = [00000001]原 = [00000001]反 = [00000001]补
但是对于负数:
[-1] = [10000001]原 = [11111110]反 = [11111111]补
可见原码, 反码和补码是完全不同的。既然原码才是被人脑直接识别并用于计算表示方式,为何还会有反码和补码呢?
首先,因为人脑可以知道第一位是符号位,在计算的时候我们会根据符号位选择对真值区域的加减。但是计算机要辨别"符号位"就必须获得全部的位的数据才可以,显然会让计算机的基础电路设计变得十分复杂! 于是人们想出了将符号位也参与运算的方法。 我们知道, 根据运算法则减去一个正数等于加上一个负数, 即: 1-1 = 1 + (-1) = 0,所以机器可以只有加法而没有减法,这样计算机运算的设计就更简单了。于是人们开始探索 将符号位参与运算,并且只保留加法的方法。
看个例子,计算十进制的表达式: 1-1=0,首先看原码的表示:
1 - 1 = 1 + (-1) = [00000001]原 + [10000001]原 = [10000010]原 = -2
如果用原码表示,让符号位也参与计算,显然对于减法来说,结果是不正确的,这也是为何计算机内部不使用原码表示一个数。
为了解决原码做减法的问题就出现了反码,此时计算十进制的表达式为: 1-1=0
1 - 1 = 1 + (-1)
= [0000 0001]原 + [1000 0001]原
= [0000 0001]反 + [1111 1110]反
= [1111 1111]反 = [1000 0000]原
= -0
可以看到用反码计算减法结果的真值部分是正确的,但是"0"的表示有点奇怪,+0和-0是一样的,而且0带符号是没有任何意义,而且要浪费[0000 0000]原和[1000 0000]原两个编码来表示0。于是补码的出现,解决了0的符号以及两个编码的问题:
1-1 = 1 + (-1) =
[0000 0001]原 + [1000 0001]原
= [0000 0001]补 + [1111 1111]补
= [0000 0000]补=[0000 0000]原
这样0用[0000 0000]表示, 而以前出现问题的-0则不存在了,而且可以用[1000 0000]表示-128:
(-1) + (-127) =
[1000 0001]原 + [1111 1111]原
= [1111 1111]补 + [1000 0001]补
= [1000 0000]补
-1-127的结果应该是-128,我们正好可以用[1000 0000]来表示-128,这样使用补码表示的范围为[-128, 127],这一点也比原码的[-127,127]好。拓展一下,对于编程中常用到的32位int类型,可以表示范围是: [-2^31, 2^31-1] ,这也是我们在应用中经常见到的定义方式。
2 位运算规则
本节的内容很多你可能学过,但是请再认真思考一遍,因为大量的算法解决思路都是从这里引申出来的
计算机采用的是二进制,二进制包括两个数码:0,1。在计算机的底层,一切运算都是基于位运算实现的,所以研究清楚位运算可以加深我们对很多基础原理的理解程度。
在算法方面,不少题目都是基于位运算拓展而来的,而且还有一定的技巧,如果不提前学一学,面试时很难想到。
位运算主要有:与、或、异或、取反、左移和右移,其中左移和右移统称移位运算,移位运算又分为算术移位和逻辑移位。
2.1 与、或、异或和取反
与运算的符号是 &,运算规则是:对于每个二进制位,当两个数对应的位都为 1 时,结果才为 1,否则结果为 0。
0 & 0=0
0 & 1=0
1 & 0=0
1 & 1=1
或运算的符号是 |,运算规则是:对于每个二进制位,当两个数对应的位都为 0 时,结果才为 0,否则结果为 1。
0 ∣ 0=0
0 ∣ 1=1
1 ∣ 0=1
1 ∣ 1=1
异或运算的符号是 ⊕(在代码中用∧ 表示异或),运算规则是:对于每个二进制位,当两个数对应的位相同时,结果为 0,否则结果为 1。
0⊕0=0
0⊕1=1
1⊕0=1
1⊕1=0
取反运算的符号是 ∼,运算规则是:对一个数的每个二进制位进行取反操作,0 变成 1,1 变成 0。
∼0=1
∼1=0
以下例子显示上述四种位运算符的运算结果,参与运算的数字都采用有符号的 8 位二进制表示。
- 46 的二进制表示是 00101110,51 的二进制表示是 00110011。考虑以下位运算的结果。
- 46&51的结果是34,对应的二进制表示是 00100010。
- 46|51 的结果是63,对应的二进制表示是 00111111。
- 46⊕51 的结果是29,对应的二进制表示是 00011101。
- ∼46 的结果是−47,对应的二进制表示是 11010001。
- ∼51 的结果是 −52,对应的二进制表示是 11001100。
2.2 移位运算
移位运算按照移位方向分类可以分成左移和右移,按照是否带符号分类可以分成算术移位和逻辑移位。
原始:0000 0110 6
右移一次:0000 0011 3 相当于除以2
左移一次:0000 1100 12 相当于乘以2
6*3 =>6*(2+1)=> 6*2+6*1
66*33=>66*(32+1) 66*32+66*1
左移运算的符号是 <<,左移运算时,将全部二进制位向左移动若干位,高位丢弃,低位补 0。对于左移运算,算术移位和逻辑移位是相同的。
右移运算的符号是 >>。右移运算时,将全部二进制位向右移动若干位,低位丢弃,高位的补位由算术移位或逻辑移位决定:
- 算术右移时,高位补最高位;
- 逻辑右移时,高位补 0。
以下例子显示移位运算的运算结果,参与运算的数字都采用有符号的 8 位二进制表示。
- 示例1:29 的二进制表示是 00011101。29左移 2 位的结果是 116,对应的二进制表示是 01110100;29 左移 3 位的结果是 −24,对应的二进制表示是 11101000。
- 示例2:50的二进制表示是 00110010。50 右移 1 位的结果是 25,对应的二进制表示是 00011001;50 右移 2 位的结果是 12,对应的二进制表示是 00001100。对于 0和正数,算术右移和逻辑右移的结果是相同的。
- 示例3:-50的二进制表示是 11001110(补码)。-50 算术右移 2 位的结果是 −13,对应的二进制表示是 11110011;−50 逻辑右移 2位的结果是 51,对应的二进制表示是 00110011。
右移运算中的算术移位和逻辑移位是不同的,计算机内部的右移运算采取的是哪一种呢?
- 对于 C/C++ 而言,数据类型包含有符号类型和无符号类型,其中有符号类型使用关键字signed 声明,无符号类型使用关键字 unsigned 声明,两个关键字都不使用时,默认是有符号类型。对于有符号类型,右移运算为算术右移;对于无符号类型,右移运算为逻辑右移。
- 对于 Java 而言,不存在无符号类型,所有的表示整数的类型都是有符号类型,因此需要区分算术右移和逻辑右移。在Java 中,算术右移的符号是 >>,逻辑右移的符号是 >>>。
2.3 移位运算与乘除法的关系
观察上面的例子可以看到,移位运算可以实现乘除操作。由于计算机的底层的一切运算都是基于位运算实现的,因此使用移位运算实现乘除法的效率显著高于直接乘除法的。
左移运算对应乘法运算。将一个数左移 k位,等价于将这个数乘以 2^k。例如,29 左移 2 位的结果是 116,等价于 29×4。当乘数不是 2 的整数次幂时,可以将乘数拆成若干项 2 的整数次幂之和,例如,a×6 等价于 (a<<2)+(a<<1)。对于任意整数,乘法运算都可以用左移运算实现,但是需要注意溢出的情况,例如在 8 位二进制表示下,29 左移 3 位就会出现溢出。
算术右移运算对应除法运算,将一个数右移 k 位,相当于将这个数除以 2^k。例如,50 右移 2 位的结果是 12,等价于 50/4,结果向下取整。
从程序实现的角度,考虑程序中的整数除法,是否可以说,将一个数(算术)右移 k 位,和将这个数除以 2^k等价?对于 0 和正数,上述说法是成立的,整数除法是向 0 取整,右移运算是向下取整,也是向 0 取整。但是对于负数,上述说法就不成立了,整数除法是向 0 取整,右移运算是向下取整,两者就不相同了。例如,(−50)>>2 的结果是 −13,而 (−50)/4 的结果是 −12,两者是不相等的。因此,将一个数(算术)右移 k 位,和将这个数除以 2^k是不等价的。算法出题这早就考虑到了这一点,因此在大部分算法题都将测试数据限制在正数和0的情况,因此可以放心的左移或者右移。
2.4 位运算常用技巧
位运算的性质有很多,此处列举一些常见性质,假设以下出现的变量都是有符号整数。
- 幂等律:a &a=a,a ∣ a=a(注意异或不满足幂等律);
- 交换律:a & b=b & a,a ∣ b=b ∣ a,a⊕b=b⊕a;
- 结合律:(a & b) & c=a & (b & c),(a ∣ b) ∣ c=a ∣ (b ∣ c),(a⊕b)⊕c=a⊕(b⊕c);
- 分配律:(a & b) ∣ c=(a ∣ c) & (b ∣ c),(a ∣ b) & c=(a & c) ∣ (b & c),(a⊕b) & c=(a & c)⊕(b & c);
- 德摩根律:∼(a & b)=(∼a) ∣ (∼b),∼(a ∣ b)=(∼a) & (∼b);
- 取反运算性质:−1=∼0,−a=∼(a−1);
- 与运算性质:a & 0=0,a & (−1)=a,a & (∼a)=0;
- 或运算性质:a ∣ 0=a;
- 异或运算性质:a⊕0=a,a⊕a=0;
- 根据上面的性质,可以得到很多处理技巧,这里列举几个:
- a & (a−1) 的结果为将 a 的二进制表示的最后一个 1 变成 0;
- (补码)a & (−a)的结果为只保留 a 的二进制表示的最后一个 1,其余的 1 都变成 0。
- 处理位操作时,还有很多技巧,不要死记硬背,理解其原理对解决相关问题有很大帮助。下面的示例中,1s和0s分别表示与x等长的一串1和一串0:
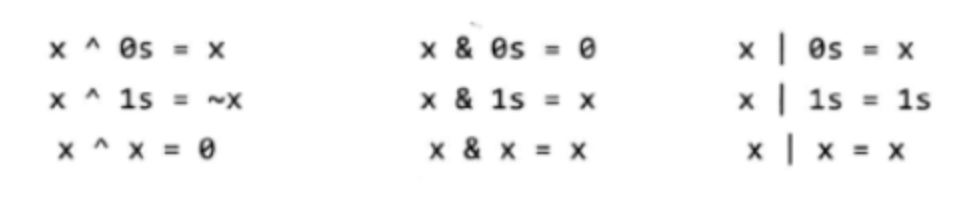
而如何获取、设置和更新某个位的数据,也有固定的套路。例如:
1.获取
该方法是将1左移i位,得到形如00010000的值。接着堆这个值与num执行”位与“操作,从而将i位之外的所有位清零,最后检查该结果是否为零。不为零说明i位为1,否则i位为0。代码如下:
boolean getBit(int num,int i){return ((num&(1<<i))!=0);
}2.设置(将某一位设置为1)
setBit先将1左移i位,得到形如00010000的值,接着堆这个值和num执行”位或“操作,这样只会改变i位的数据。这样除i位外的位均为零,故不会影响num的其余位。代码如下:
int setBit(int num,int i){return num |(1<<i);
}3. 清零(将某一位设置为0)
该方法与setBit相反,首先将1左移i位获得形如00010000的值,对这个值取反进而得到类似11101111的值,接着对该值和num执行”位与“,故而不会影响到num的其余位,只会清零i位。
int clearBit(int num ,int i){int mask=~(1<<i);return num&mask;}4.更新
这个方法是将setBit和clearBit合二为一,首先用诸如11101111的值将num的第i位清零。接着将待写入值v左移i位,得到一个i位为v但其余位都为0的数。最后对之前的结果执行”位或“操作,v为1这num的i位更新为1,否则为0:
int updateBit(int num,int i,int v){int mask=~(1<<i);return (num&mask)|(v<<i);
}相关文章:
理解位运算的规则
关卡名 理解位运算的规则 我会了✔️ 内容 1.理解位运算的基本规则 ✔️ 2.理解移位的原理以及与乘除的关系 ✔️ 3.掌握位运算的常用技巧 ✔️ 在学习位操作之前,我们先明确数据在计算机中怎么表示的。我们明确原码、反码和补码的概念和表示方法,之…...
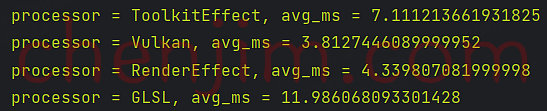
Android Bitmap 使用Vukan、RenderEffect、GLSL实现模糊
文章目录 Android Bitmap 使用Vukan、RenderEffect、GLSL实现模糊使用 RenderEffect 模糊使用 Vukan 模糊使用 GLSL 模糊RS、Vukan、RenderEffect、GLSL 效率对比 Android Bitmap 使用Vukan、RenderEffect、GLSL实现模糊 本文首发地址 https://blog.csdn.net/CSqingchen/articl…...

Vue H5页面长按保存为图片
安装依赖:npm install html2canvas -d <template><div class"index"><div id"captureId" class"capture" v-show"firstFlag"><ul><li>1</li><li>2</li><li>3<…...
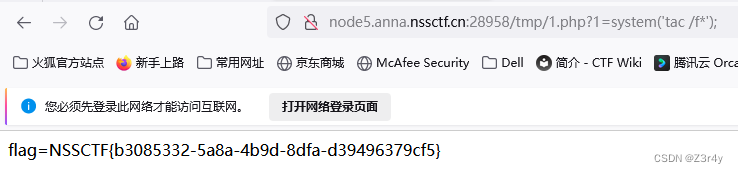
【Web】UUCTF 2022 新生赛 个人复现
目录 ①websign ②ez_rce ③ez_upload ④ez_unser ⑤ezsql ⑥ezpop ⑦funmd5 ⑧phonecode ⑨ezrce ①websign 右键打不开,直接抓包发包看源码 ②ez_rce “反引号” 在PHP中会被当作SHELL命令执行 ?codeprintf(l\s /); ?codeprintf(ta\c /ffffffffffl…...

设置python下载包代理
使用场景 正常网络情况下我们安装如果比较多的python包时,会选择使用pip install -r requirements.txt -i https://pypi.douban.com/simple --trusted-hostpypi.douban.com这种国内的镜像来加快下载速度。 但是,当这台被限制上网时(公司安全…...

nginx 配置前端项目添加https
可申请阿里云免费证书 步骤省略… nginx 配置 server {listen 8050; #默认80端口 如果需要所有访问地址都是https 需要注释listen 8443 ssl; #https 访问的端口 ,默认443server_name 192.168.128.XX; #域名 或 ip# 增加ssl#填写证书文件…...

人群计数CSRNet的pytorch实现
本文中对CSRNet: Dilated Convolutional Neural Networks for Understanding the Highly Congested Scenes(CVPR 2018)中的模型进行pytorch实现 import torch;import torch.nn as nn from torchvision.models import vgg16 vggvgg16(pretrained1)import…...
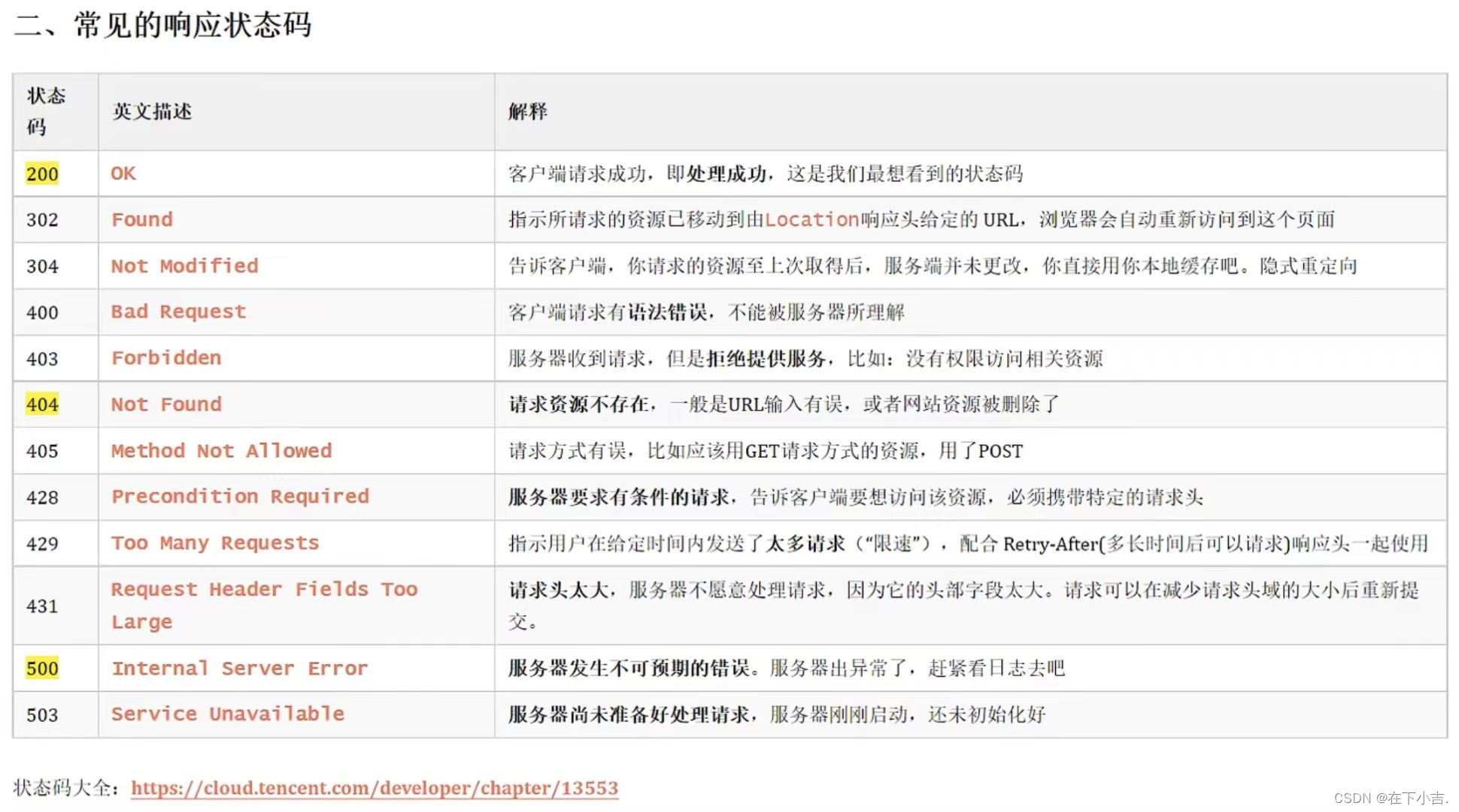
【HTTP协议】简述HTTP协议的概念和特点
🎊专栏【网络编程】 🍔喜欢的诗句:更喜岷山千里雪 三军过后尽开颜。 🎆音乐分享【如愿】 🥰欢迎并且感谢大家指出小吉的问题 文章目录 🌺概念🌺特点🎄请求协议🎄响应协议…...

经典神经网络——AlexNet模型论文详解及代码复现
一、背景 AlexNet是在2012年由Alex Krizhevsky等人提出的,该网络在2012年的ImageNet大赛上夺得了冠军,并且错误率比第二名高了很多。Alexnet共有8层结构,前5层为卷积层,后三层为全连接层。 论文地址:ImageNet Classif…...

flutter开发实战-轮播Swiper更改Custom_layout样式中Widget层级
flutter开发实战-轮播Swiper更改Custom_layout样式中Widget层级 在之前的开发过程中,需要实现卡片轮播效果,但是卡片轮播需要中间大、两边小一些的效果,这里就使用到了Swiper。具体效果如视频所示 添加链接描述 这里需要的效果是中间大、两边…...
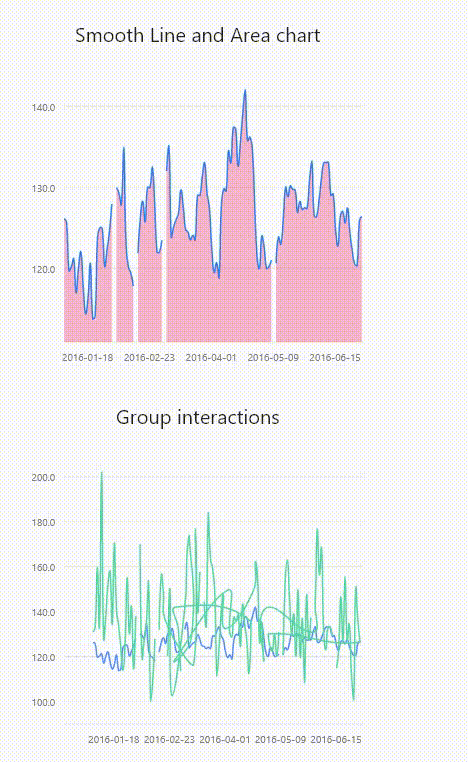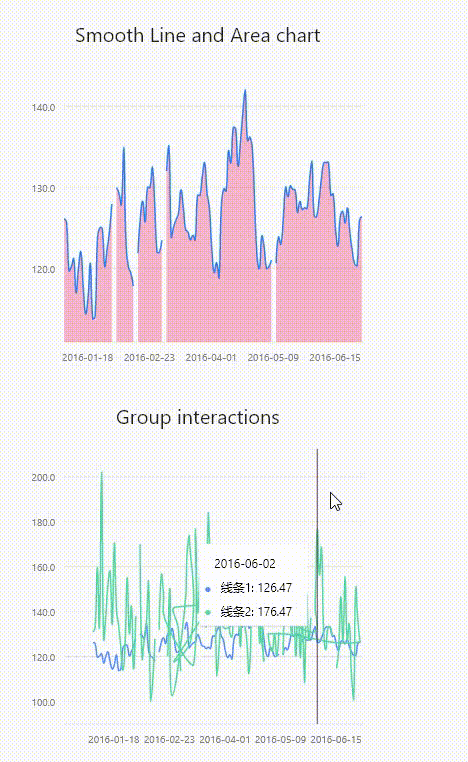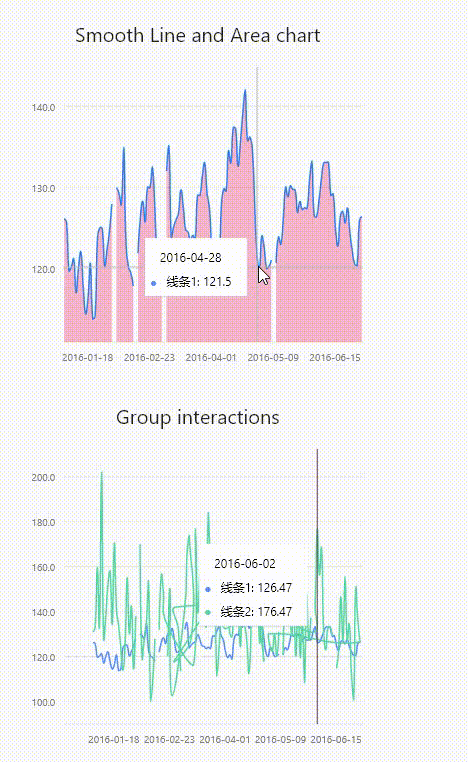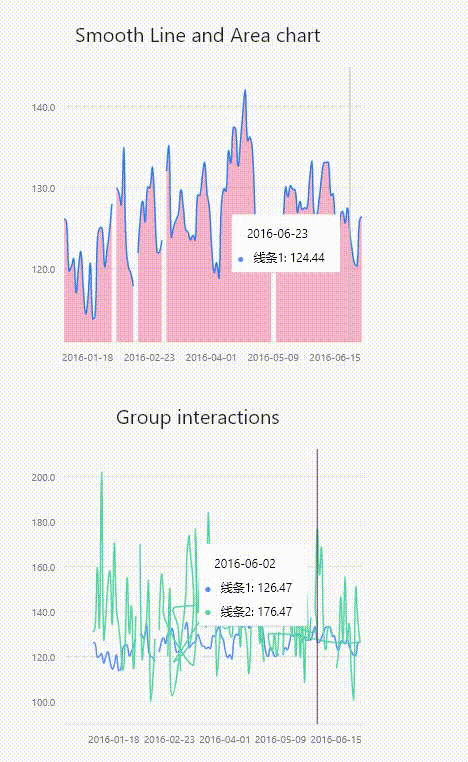
【Flutter】graphic图表实现自定义tooltip
renderer graphic中tooltip的TooltipGuide类提供了renderer方法,接收三个参数Size类型,Offset类型,Map<int, Tuple>类型。可查到的文档是真的少,所以只能在源码中扒拉例子,做符合需求的修改。 官方github示例 …...
手机上的记事本怎么打开?安卓手机通用的记事本APP
有不少上班族发现,自己想要在电脑上随手记录一些工作文字内容,直接使用电脑上的记事本工具来编辑文字是比较便捷的。但是如果想要在手机上记录文字内容,就找不到手机上的记事本了。那么手机上的记事本怎么打开?安卓手机通用的记事…...

一起学docker系列之十五深入了解 Docker Network:构建容器间通信的桥梁
目录 1 前言2 什么是 Docker Network3 Docker Network 的不同模式3.1 桥接模式(Bridge)3.2 Host 模式3.3 无网络模式(None)3.4 容器模式(Container) 4 Docker Network 命令及用法4.1 docker network ls4.2 …...
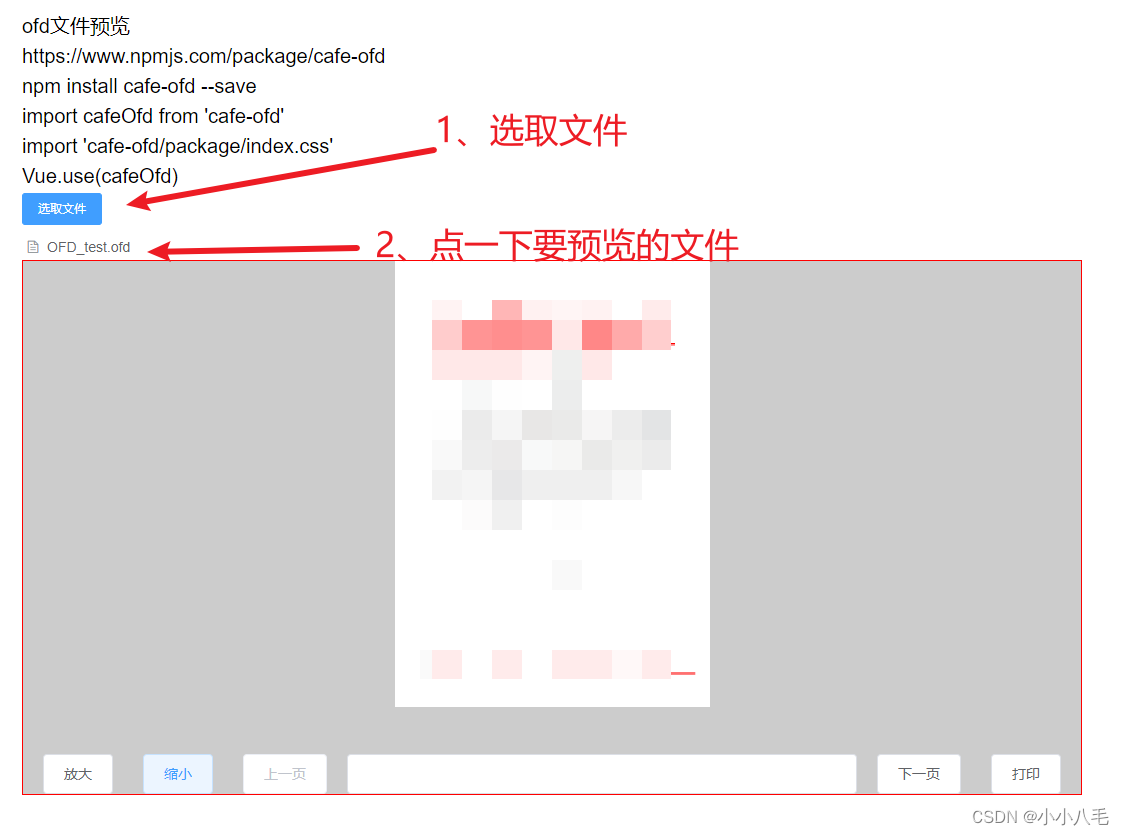
前端OFD文件预览(vue案例cafe-ofd)
0、提示 下面只有vue的使用示例demo ,官文档参考 cafe-ofd - npm 其他平台可以参考 ofd - npm 官方线上demo: ofd 1、安装包 npm install cafe-ofd --save 2、引入 import cafeOfd from cafe-ofd import cafe-ofd/package/index.css Vue.use(cafeOfd) 3、使…...

Java[list/set]通用遍历方法之Iterator
需求:输入一个字符串 将其拆解成单个汉字 然后一行一个输出 这里要求使用到Arraylist集合实现方法Itrator遍历的原理import java.util.ArrayList; import java.util.Collection; import java.util.Iterator;public class Main{public static void main(String[] arg…...
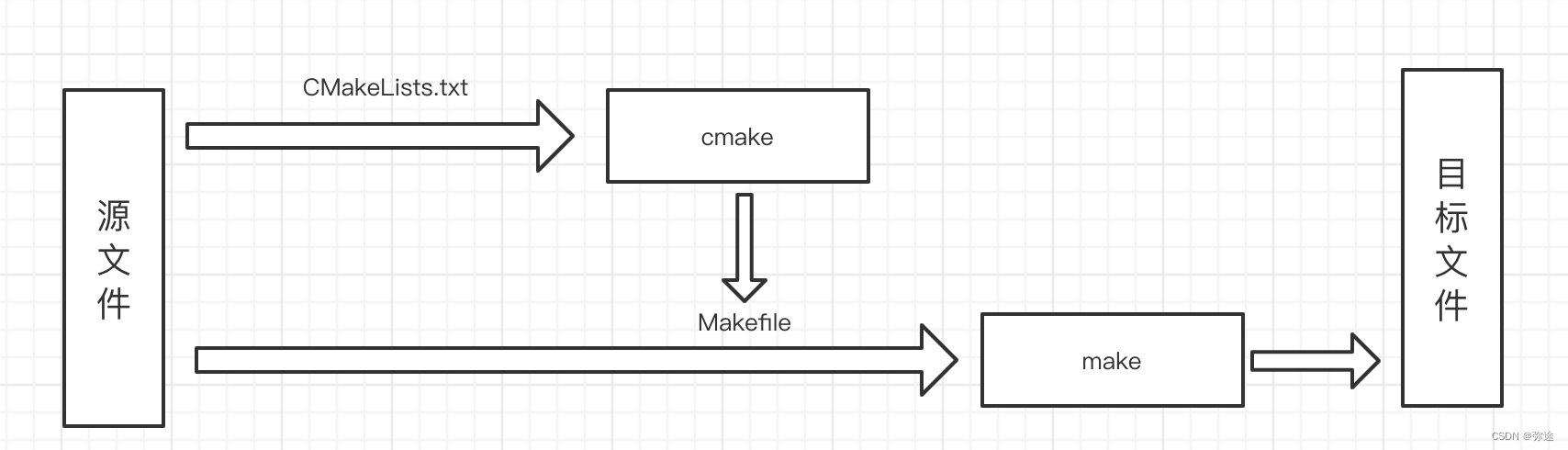
ubuntu/vscode下的c/c++开发之-CMake语法与练习
Cmake学习 1 语法特性介绍 基本语法格式:指令(参数 1 参数 2...) 参数使用括弧括起参数之间使用空格或分号分开 指令是大小写无关的,参数和变量是大小写相关的 set(HELLO hello.cpp) add_executable(hello main.cpp hello.cpp) ADD_EXECUTABLE(hello ma…...
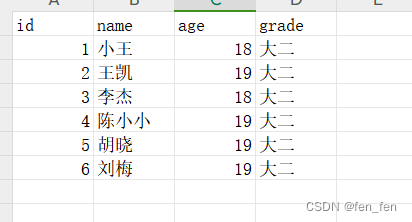
Java(119):ExcelUtil工具类(org.apache.poi读取和写入Excel)
ExcelUtil工具类(XSSFWorkbook读取和写入Excel),入参和出参都是:List<Map<String,Object>> 一、读取Excel testdata.xlsx 1、new XSSFWorkbook对象 File file = new File(filePath); FileInputStream fis = new FileInputStream(file);…...

Kong处理web服务跨域
前言 好久没写文章了,大概有半年多了,这半年故事太多,本文写不下,就写写文章标题问题! 问题描述 关于跨域的本质问题我这里不过多介绍,详细请看历史文章 跨域产生的原因以及常见的解决方案。 我这边是新…...
Kotlin学习——kt里的作用域函数scope function,let,run,with,apply,also
Kotlin 是一门现代但已成熟的编程语言,旨在让开发人员更幸福快乐。 它简洁、安全、可与 Java 及其他语言互操作,并提供了多种方式在多个平台间复用代码,以实现高效编程。 https://play.kotlinlang.org/byExample/01_introduction/02_Functio…...

informer辅助笔记:utils/timefeatures.py
定义了一套与时间特征相关的类和函数,旨在从时间序列数据中提取有用的时间特征,以支持各种时间序列分析和预测任务 from typing import Listimport numpy as np import pandas as pd from pandas.tseries import offsets from pandas.tseries.frequenc…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

基于Java Swing的电子通讯录设计与实现:附系统托盘功能代码详解
JAVASQL电子通讯录带系统托盘 一、系统概述 本电子通讯录系统采用Java Swing开发桌面应用,结合SQLite数据库实现联系人管理功能,并集成系统托盘功能提升用户体验。系统支持联系人的增删改查、分组管理、搜索过滤等功能,同时可以最小化到系统…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...
