【深度优先】LeetCode1932:合并多棵二叉搜索树
作者推荐
动态规划LeetCode2552:优化了6版的1324模式
题目
给你 n 个 二叉搜索树的根节点 ,存储在数组 trees 中(下标从 0 开始),对应 n 棵不同的二叉搜索树。trees 中的每棵二叉搜索树 最多有 3 个节点 ,且不存在值相同的两个根节点。在一步操作中,将会完成下述步骤:
选择两个 不同的 下标 i 和 j ,要求满足在 trees[i] 中的某个 叶节点 的值等于 trees[j] 的 根节点的值 。
用 trees[j] 替换 trees[i] 中的那个叶节点。
从 trees 中移除 trees[j] 。
如果在执行 n - 1 次操作后,能形成一棵有效的二叉搜索树,则返回结果二叉树的 根节点 ;如果无法构造一棵有效的二叉搜索树,返回 null 。
二叉搜索树是一种二叉树,且树中每个节点均满足下述属性:
任意节点的左子树中的值都 严格小于 此节点的值。
任意节点的右子树中的值都 严格大于 此节点的值。
叶节点是不含子节点的节点。
示例 1:
输入:trees = [[2,1],[3,2,5],[5,4]]
输出:[3,2,5,1,null,4]
解释:
第一步操作中,选出 i=1 和 j=0 ,并将 trees[0] 合并到 trees[1] 中。
删除 trees[0] ,trees = [[3,2,5,1],[5,4]] 。
在第二步操作中,选出 i=0 和 j=1 ,将 trees[1] 合并到 trees[0] 中。
删除 trees[1] ,trees = [[3,2,5,1,null,4]] 。
结果树如上图所示,为一棵有效的二叉搜索树,所以返回该树的根节点。
示例 2:
输入:trees = [[5,3,8],[3,2,6]]
输出:[]
解释:
选出 i=0 和 j=1 ,然后将 trees[1] 合并到 trees[0] 中。
删除 trees[1] ,trees = [[5,3,8,2,6]] 。
结果树如上图所示。仅能执行一次有效的操作,但结果树不是一棵有效的二叉搜索树,所以返回 null 。
示例 3:
输入:trees = [[5,4],[3]]
输出:[]
解释:无法执行任何操作。
参数范围:
n == trees.length
1 <= n <= 5 * 104
每棵树中节点数目在范围 [1, 3] 内。
输入数据的每个节点可能有子节点但不存在子节点的子节点
trees 中不存在两棵树根节点值相同的情况。
输入中的所有树都是 有效的二叉树搜索树 。
1 <= TreeNode.val <= 5 * 104.
分析
正确分析
能合并则合并,如果合并树的数量为1,则正确。
不需要考虑:叶子相同,那个叶子合并根的问题,两个叶子相同,那个叶子合并最后都不会是合法的搜索树。
错误分析
vMin 记录各子树的最小值,vMax记录各子树的最大值。 成为左子树的条件:一,叶子的值等子树根的值。 二,子树的最大值小于父树的值。成为右子树的条件:一,叶子的值等子树根的值。 二,子树的最小值大于父树的值。
错误原因
父子符合条件,祖孙不符合条件。
解决方法
判断是否是合法的树。
变量解释
| vMin[i] | 以trees[i]为根的树的最小节点值 |
| vMax[i] | 以trees[i]为根的树的最大节点值 |
| mValueIndex | key:trees[i]根节点的值;value:i。 |
代码
struct TreeNode {
int val;
TreeNode* left;
TreeNode* right;
TreeNode() : val(0), left(nullptr), right(nullptr) {}
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
TreeNode(int x, TreeNode* left, TreeNode* right) : val(x), left(left), right(right) {}
};
class Solution {
public:
TreeNode* canMerge(vector<TreeNode*>& trees) {
m_c = trees.size();
vector vMin(m_c), vMax(m_c);
unordered_map<int, int> mValueIndex;
for (int i = 0; i < m_c; i++)
{
const auto& p = trees[i];
mValueIndex[p->val] = i;
vMin[i] = (nullptr == p->left) ? p->val : p->left->val;
vMax[i] = (nullptr == p->right) ? p->val : p->right->val;
}
for (int i = 0; i < m_c; i++)
{
std::cout << "i " << i;
const auto& p = trees[i];
if ((nullptr != p->left) && mValueIndex.count(p->left->val))
{
const int index = mValueIndex[p->left->val];
if (vMax[index] < p->val)
{
std::cout << "index " << index;
vMin[i] = min(vMin[i], vMin[index]);
p->left = trees[index];
mValueIndex.erase(mValueIndex.find(p->left->val));
}
}
if ((nullptr != p->right) && mValueIndex.count(p->right->val))
{
const int index = mValueIndex[p->right->val];
if (vMin[index] > p->val)
{
std::cout << "r " << index;
vMax[i] = max(vMax[i], vMax[index]);
p->right = trees[index];
mValueIndex.erase(p->right->val);
}
}
std::cout << std::endl;
}
if (mValueIndex.size() > 1) return nullptr;
auto [suc, tmp1, tmp2] = DFS(trees[mValueIndex.begin()->second]);
if (!suc)
{
return nullptr;
}
return trees[mValueIndex.begin()->second];
}
std::tuple<bool, int, int> DFS(TreeNode* root)
{
int iMin = root->val;
int iMax = root->val;
if (nullptr != root->left)
{
auto [suc, iRetMin, iRetMax] = DFS(root->left);
if ((!suc)||( iRetMax >= root->val))
{
return std::make_tuple(false, 0, 0);
}
iMin = iRetMin;
}
if (nullptr != root->right)
{
auto [suc, iRetMin, iRetMax] = DFS(root->right);
if ((!suc) || (iRetMin <= root->val))
{
return std::make_tuple(false, 0, 0);
}
iMax = iRetMax;
}
return std::make_tuple(true, iMin, iMax);
}
int m_c;
};
优化
分析
最后总是要判断是否是合法树,那合并树的时候就不需要判断了。这样会产生新问题:
三个子树成环,两个子树合并成树。 合并了3次符合条件,但不是一棵树,而是两个连通区域。
解法方法如下:
一,判断唯一的树的节点数是否合法。
二,并集查找,看有几个连通区域。
三,判断有几个合法的根(不存在值相同的叶子),从根开始合并。
四,获取树的中顺遍历,看是否是严格递增。且节点数是否正确。
判断合法的根的代码
class Solution {
public:
TreeNode* canMerge(vector<TreeNode*>& trees) {
m_c = trees.size();
unordered_set setLeaf;
for (int i = 0; i < m_c; i++)
{
auto& p = trees[i];
m_mValuePtr[p->val] = p;
if (nullptr != p->left)
{
setLeaf.emplace(p->left->val);
}
if (nullptr != p->right)
{
setLeaf.emplace(p->right->val);
}
}
TreeNode* root = nullptr;
for (int i = 0; i < m_c; i++)
{
if (setLeaf.count(trees[i]->val))
{
continue;//和某个叶子起点重合,不是根
}
if (nullptr != root)
{
return nullptr;//不可能有两个根
}
root = trees[i];
}
if( nullptr == root)
{
return nullptr;
}
DFSBuild(root);
if (m_mValuePtr.size() != 1 )
{
return nullptr;
}
auto [suc, tmp1, tmp2] = DFS(root);
if (!suc)
{
return nullptr;
}
return root;
}
void DFSBuild(TreeNode* root)
{
auto Build = [&](TreeNode*& node)
{
if ((nullptr != node) && (m_mValuePtr.count(node->val)))
{
node = m_mValuePtr[node->val];
m_mValuePtr.erase(node->val);
DFSBuild(node);
}
};
Build(root->left);
Build(root->right);
}
std::tuple<bool, int, int> DFS(TreeNode* root)
{
int iMin = root->val;
int iMax = root->val;
if (nullptr != root->left)
{
auto [suc, iRetMin, iRetMax] = DFS(root->left);
if ((!suc) || (iRetMax >= root->val))
{
return std::make_tuple(false, 0, 0);
}
iMin = iRetMin;
}
if (nullptr != root->right)
{
auto [suc, iRetMin, iRetMax] = DFS(root->right);
if ((!suc) || (iRetMin <= root->val))
{
return std::make_tuple(false, 0, 0);
}
iMax = iRetMax;
}
return std::make_tuple(true, iMin, iMax);
}
unordered_map<int, TreeNode*> m_mValuePtr;
int m_c;
};
中序遍历
class Solution {
public:
TreeNode* canMerge(vector<TreeNode*>& trees) {
m_c = trees.size();
int iNodeCount = 0;
for (int i = 0; i < m_c; i++)
{
const auto& p = trees[i];
m_mValuePtr[p->val] = p;
iNodeCount += (1 + (nullptr != p->left) + (nullptr != p->right));
}
for (int i = 0; i < m_c; i++)
{
auto Build = [&](TreeNode*& node)
{
if ((nullptr != node) && (m_mValuePtr.count(node->val)))
{
node = m_mValuePtr[node->val];
m_mValuePtr.erase(node->val);
}
};
Build(trees[i]->left);
Build(trees[i]->right);
}
if (m_mValuePtr.size() != 1 )
{
return nullptr;
}
vector vNode;
DFSNLR(vNode, m_mValuePtr.begin()->second);
if (vNode.size() + m_c-1 != iNodeCount)
{
return nullptr;
}
for (int i = 1; i < vNode.size(); i++)
{
if (vNode[i] <= vNode[i - 1])
{
return nullptr;
}
}
return m_mValuePtr.begin()->second;
}
void DFSNLR(vector& v,TreeNode* root)
{
if (nullptr == root)
{
return ;
}
DFSNLR(v,root->left);
v.emplace_back(root->val);
DFSNLR(v,root->right);
}
unordered_map<int, TreeNode*> m_mValuePtr;
int m_c;
};
中序遍历优化
vNode我们只需要读取最后一个值,所以可以用一个整形变量pre代替。
class Solution {public:TreeNode* canMerge(vector<TreeNode*>& trees) {m_c = trees.size();int iNodeCount = 0;for (int i = 0; i < m_c; i++){const auto& p = trees[i];m_mValuePtr[p->val] = p;iNodeCount += (1 + (nullptr != p->left) + (nullptr != p->right));}for (int i = 0; i < m_c; i++){auto Build = [&](TreeNode*& node){if ((nullptr != node) && (m_mValuePtr.count(node->val))){node = m_mValuePtr[node->val];m_mValuePtr.erase(node->val); }};Build(trees[i]->left);Build(trees[i]->right);}if (m_mValuePtr.size() != 1 ){return nullptr;}int pre=-1;if (!DFSNLR(m_mValuePtr.begin()->second, pre) || (m_iNodeSize + m_c - 1 != iNodeCount)){return nullptr;}return m_mValuePtr.begin()->second;}bool DFSNLR(TreeNode* root, int& pre){if ((root->left) && (!DFSNLR(root->left, pre))){return false;}m_iNodeSize++;if (root->val <= pre){return false;}pre = root->val;if ((root->right) && (!DFSNLR(root->right, pre))){return false;}return true;} int m_iNodeSize = 0;unordered_map<int, TreeNode*> m_mValuePtr;int m_c;};
2023年6月旧版
class Solution {
public:
TreeNode* canMerge(vector<TreeNode*>& trees) {
vector<TreeNode*> vRoot(5 * 10000 + 1);
std::set setNums;
for (auto& ptr : trees)
{
vRoot[ptr->val] = ptr;
setNums.emplace(ptr->val);
if (nullptr != ptr->left)
{
setNums.emplace(ptr->left->val);
}
if (nullptr != ptr->right)
{
setNums.emplace(ptr->right->val);
}
}
int iNodeNum = setNums.size();
for (auto& ptr : trees)
{
if ((nullptr != ptr->left) && (nullptr != vRoot[ptr->left->val]))
{
ptr->left = vRoot[ptr->left->val];
vRoot[ptr->left->val] = nullptr;
}
if ((nullptr != ptr->right) && (nullptr != vRoot[ptr->right->val]))
{
ptr->right = vRoot[ptr->right->val];
vRoot[ptr->right->val] = nullptr;
}
}
TreeNode* pRoot = nullptr;
for (auto ptr : vRoot)
{
if (nullptr == ptr)
{
continue;
}
if (nullptr != pRoot)
{
return nullptr;//两个根
}
pRoot = ptr;
}
if (nullptr == pRoot)
{
return nullptr;
}
if (iNodeNum != DFSNum(pRoot))
{
return nullptr;
}
int iMin, iMax;
bool bRet = DFS(iMin, iMax, pRoot);
return bRet ? pRoot : nullptr;
}
bool DFS(int& iMin, int& iMax, TreeNode* pNode)
{
iMin = iMax = pNode->val;
if ((nullptr != pNode->left))
{
int iMinLeft, iMaxLeft;
if (!DFS(iMinLeft, iMaxLeft, pNode->left))
{
return false;
}
if (iMaxLeft >= pNode->val)
{
return false;
}
iMin = iMinLeft;
}
if ((nullptr != pNode->right))
{
int iMinRight, iMaxRight;
if (!DFS(iMinRight, iMaxRight, pNode->right))
{
return false;
}
if (iMinRight <= pNode->val)
{
return false;
}
iMax = iMaxRight;
}
return true;
}
int DFSNum(TreeNode* pNode)
{
if (nullptr == pNode)
{
return 0;
}
return 1 + DFSNum(pNode->left) + DFSNum(pNode->right);
}
};
扩展阅读
视频课程
有效学习:明确的目标 及时的反馈 拉伸区(难度合适),可以先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快
速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
相关下载
想高屋建瓴的学习算法,请下载《喜缺全书算法册》doc版
https://download.csdn.net/download/he_zhidan/88348653
| 我想对大家说的话 |
|---|
| 闻缺陷则喜是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境:
VS2022 C++17

相关文章:

【深度优先】LeetCode1932:合并多棵二叉搜索树
作者推荐 动态规划LeetCode2552:优化了6版的1324模式 题目 给你 n 个 二叉搜索树的根节点 ,存储在数组 trees 中(下标从 0 开始),对应 n 棵不同的二叉搜索树。trees 中的每棵二叉搜索树 最多有 3 个节点 ࿰…...
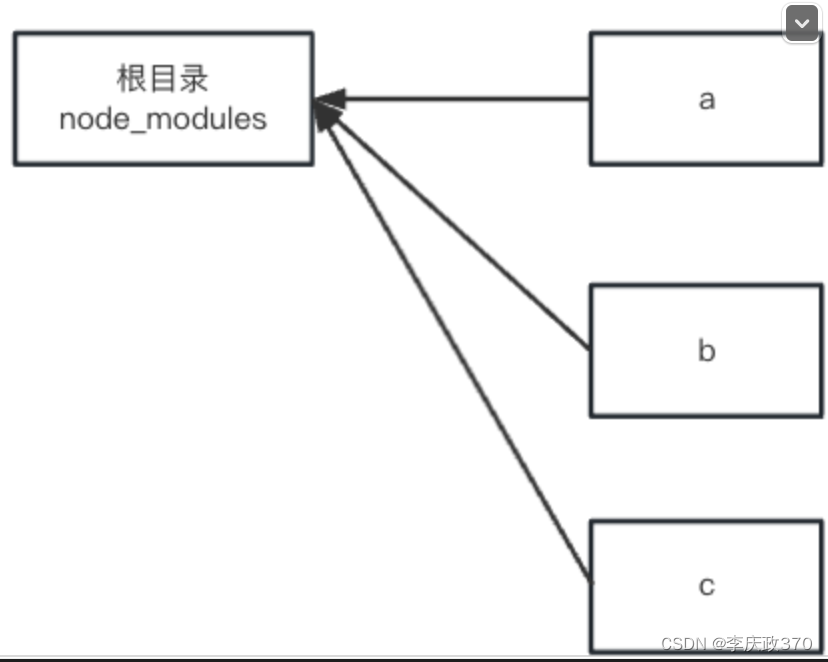
monorepo多项目管理主流实现方式:1.learn + yarn/npm workspace 2.pnpm
npm域级包 随着npm包越来越多,而且包名也只能是唯一的,如果一个名字被别人占了,那你就不能再使用这个名字;假设我想要开发一个utils包,但是张三已经发布了一个utils包,那我的包名就不能叫utils了ÿ…...

【斗罗二】暗杀霍雨浩行动,马小桃霸气回击,江楠楠首秀武魂兔兔
Hello,小伙伴们,我是拾荒君。 《斗罗大陆Ⅱ绝世唐门》第25集更新了!和小伙伴们一样,一更新,拾荒君就急不可待地观看这一集。故事情节高潮迭起,尤其是霍雨浩与王冬面对六名杀手的惊险场景,真是让人心跳加速…...

[ 蓝桥杯Web真题 ]-年度明星项目
目录 引入 介绍 准备 目标 效果 规定 思路 知识补充 解答参考 引入 hello,大家好!我注意到了之前发的一篇蓝桥杯Web应用开发的文章是关注度最高的,可能大部分关注我的小伙伴对蓝桥杯Web应用开发比较感兴趣,或者想要参加…...

Maven终端打包时报Unknown lifecycle phase “.test.skip=true“
错误实例代码 mvn clean package -Dmaven.test.skiptrue 再windows的cmd窗口进行项目打包,需要将参数用英文符号包裹起来“ ” 【正确的实例】:mvn clean package ’-Dmaven.test.skiptrue‘ PS D:\BaiduNetdiskDownload\qian\Springboot-Vue\bi…...
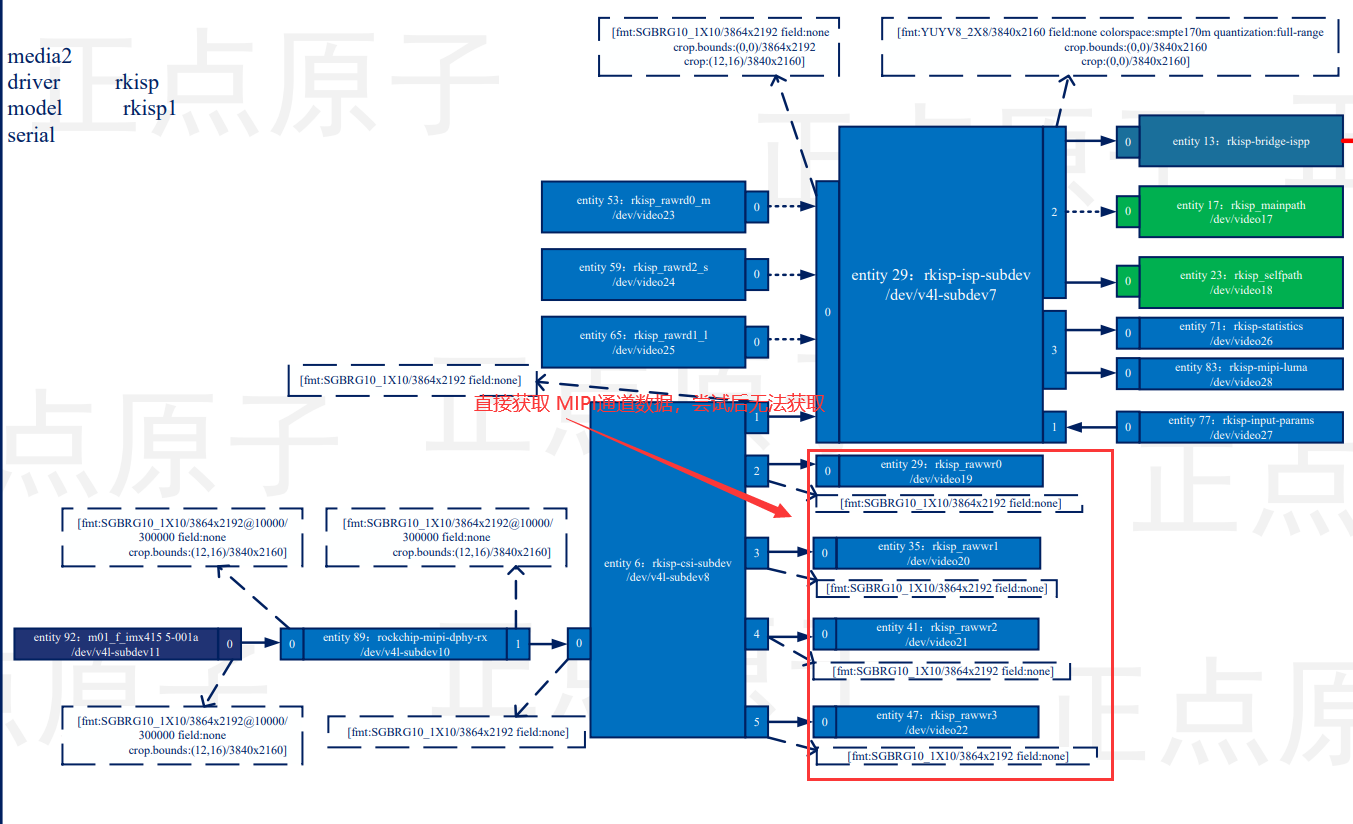
Linux MIPI 调试中常见的问题
一、概述 做嵌入式工作的小伙伴知道,有时候程序编写没有调试过程中费时,之间笔记里有 MIPI 摄像头驱动开发的过程,有需要的小伙伴可以参考:Linux RN6752 驱动编写。而我也是第一次琢磨 MIPI 协议,其中有很多不明白的地…...
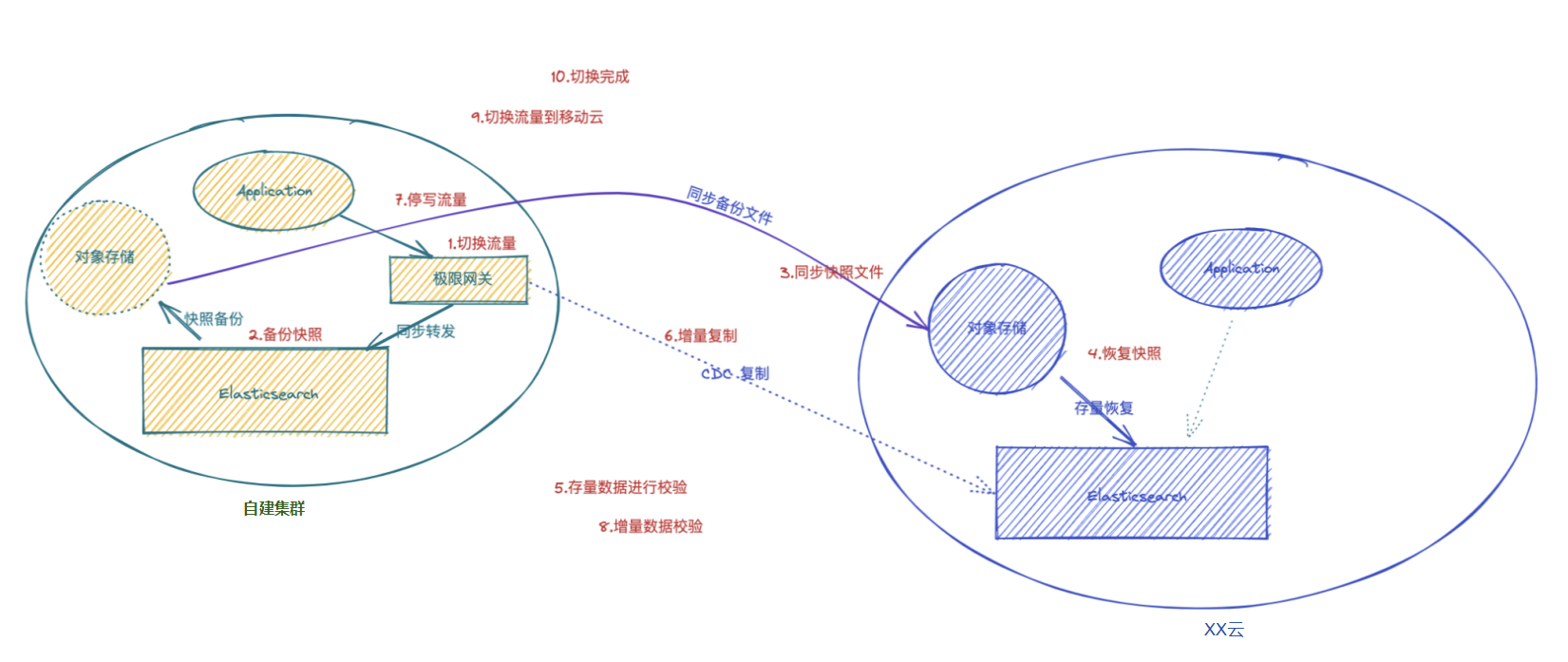
使用极限网关助力 ES 集群无缝升级、迁移上/下云
在工作中大家可能会遇到以下这些场景: 自建 ES 集群需要平滑迁移到 XX 云;从 XX 云将 ES 集群迁移到自建机房;ES 集群进行跨版本升级,同时保留回退能力; 这些场景往往都还有个共同的需求:迁移过程要保证业…...

RedisTemplate的配置和讲解以及和StringRedisTemplate的区别
本文主要讲redisTempalte的几种常用的序列化方式 string,我们大部分情况下都希望存入redis的数据可读性强一些,并且value也不总是一个规则的类型,所以这里也是不用json序列化的原因,可以更自由方便,下边提供配置方法 …...
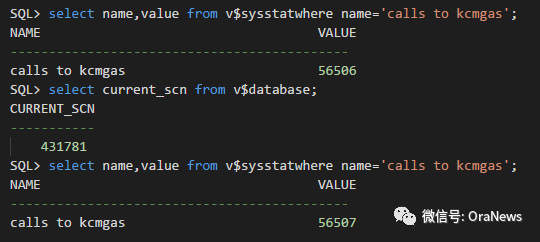
在oracle中的scn技术
SCN可以说是Oracle中一个很基础的部分,但同时它也是一个很重要的。它是系统中维持数据的一致性和顺序恢复的重要标志,是数据库非常重要的一种数据结构。 转载:深入剖析 - Oracle SCN机制详细解读 - 知乎 (zhihu.com)https://zhuanlan.zhihu.…...

LINUX 嵌入式C编程--信号编程
基本概念 信号是事件发生时对进程的通知机制,也可以把它称为软件中断。信号与硬件中断的相似之处在于能够打断程序当前执行的正常流程,其实是在软件层次上对中断机制的一种模拟。信号提供了一种处理异步事件的方法。 信号目的 **信号的目的是用来通信…...

Linux:优化原则
web系统的优化原则: 从单机到集群 对Linux系统自身的优化原则:...
HarmonyOs 4 (一) 认识HarmonyOs
目录 一 HarmonyOs 背景1.1 发展时间线1.2 背景分析1.2.1 新场景1.2.2 新挑战1.2.3 鸿蒙生态迎接挑战 二 HarmonyOS简介2.1 OpenHarmony2.2 HarmonyOS Connect2.3 HarmonyOS Next**2.4 ArkTS (重点掌握)****2.5 ArkUI** 三 鸿蒙生态应用核心技术理念**3.…...
System.out.println隐藏字符串
昨天开发的时候遇到一个坑,这个坑几乎浪费了我一整天时间,我甚至现在都不知道其原因。 开发环境 macOS Ventura 13.4 IntelliJ IDEA 2023.1.2 现象 我用java的各种httpclient获取网络上的一个文本文件,获取的文本文件的内容使用System.ou…...

Java中的线程池你了解多少?
🌈🌈🌈今天给大家分享的是Java标准库中的线程池,以及线程池的自定义实现。 清风的CSDN博客 🛩️🛩️🛩️希望我的文章能对你有所帮助,有不足的地方还请各位看官多多指教,…...
leetCode 131.分割回文串 + 动态规划 + 回溯算法 + 优化 + 图解 + 笔记
我的往期文章: leetCode 647.回文子串 动态规划 优化空间 / 中心扩展法 双指针-CSDN博客https://blog.csdn.net/weixin_41987016/article/details/133883091?spm1001.2014.3001.5501leetCode 131.分割回文串 回溯算法 图解 笔记-CSDN博客https://blog.csdn.n…...
【傻瓜级JS-DLL-WINCC-PLC交互】3.JS-DLL进行交互
思路 JS-DLL-WINCC-PLC之间进行交互,思路,先用Visual Studio创建一个C#的DLL控件,然后这个控件里面嵌入浏览器组件,实现JS与DLL通信,然后DLL放入到WINCC里面的图形编辑器中,实现DLL与WINCC的通信。然后PLC与…...

深度学习手势识别算法实现 - opencv python 计算机竞赛
文章目录 1 前言2 项目背景3 任务描述4 环境搭配5 项目实现5.1 准备数据5.2 构建网络5.3 开始训练5.4 模型评估 6 识别效果7 最后 1 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 深度学习手势识别算法实现 - opencv python 该项目较为新颖…...

2023-12-01 AIGC-自动生成ppt的AI工具
摘要: 2023-12-01 AIGC-自动生成ppt-记录 自动生成ppt: BoardMix boardmix 一键生成ppt boardmix是一款基于云的ai设计软件,允许创建用于各种目的的自定义演示文稿、ai绘画,ai生成思维导图等。以下是它的一些功能: 可定制的模板 - 它有一个…...
NoSQL 数据建模错误会降低性能
数据建模错误是破坏性能的最简单方法之一。当您使用 NoSQL 时,特别容易搞砸,(讽刺的是)NoSQL 往往用于对性能最敏感的工作负载。NoSQL 数据建模最初可能看起来非常简单:只需对数据进行建模以适应应用程序的访问模式。但…...
在Android上搭建一个NDK项目
首先New Project,选择Native C,点击Next。 填入项目名称和包名,点击Next。 这里我们选择Cmake默认的C版本。 创建好的项目目录,里面比我们正常的Android项目多了一个cpp目录 打开MainActivity。里面定义了一个jni方法stringFromJN…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

多元隐函数 偏导公式
我们来推导隐函数 z z ( x , y ) z z(x, y) zz(x,y) 的偏导公式,给定一个隐函数关系: F ( x , y , z ( x , y ) ) 0 F(x, y, z(x, y)) 0 F(x,y,z(x,y))0 🧠 目标: 求 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z、 …...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...
