leetCode 131.分割回文串 + 动态规划 + 回溯算法 + 优化 + 图解 + 笔记
我的往期文章:
leetCode 647.回文子串 动态规划 + 优化空间 / 中心扩展法 + 双指针-CSDN博客![]() https://blog.csdn.net/weixin_41987016/article/details/133883091?spm=1001.2014.3001.5501leetCode 131.分割回文串 + 回溯算法 + 图解 + 笔记-CSDN博客
https://blog.csdn.net/weixin_41987016/article/details/133883091?spm=1001.2014.3001.5501leetCode 131.分割回文串 + 回溯算法 + 图解 + 笔记-CSDN博客![]() https://blog.csdn.net/weixin_41987016/article/details/134700907?spm=1001.2014.3001.5501(一)利用动态规划来优化判断回文子串
https://blog.csdn.net/weixin_41987016/article/details/134700907?spm=1001.2014.3001.5501(一)利用动态规划来优化判断回文子串
- 利用动态规划高效地事先一次性计算出, 针对一个字符串
s, 它的任何子串是否是回文字串, 然后在我们的回溯函数中直接查询即可, 省去了双指针移动判定这一步骤.(来自代码随想录Carl老师的原话)原文链接:代码随想录 (programmercarl.com)
>>思路和分析
回文子串:讲究的是这个字符串里边左右两边是对称的,左右两边的元素是相同的。如果只判断这个字符串的最左面和最右面这两个元素相同的情况下,还知道中间的子串已经是回文的,那么就可以直接判断整个字符串它就是回文子串。
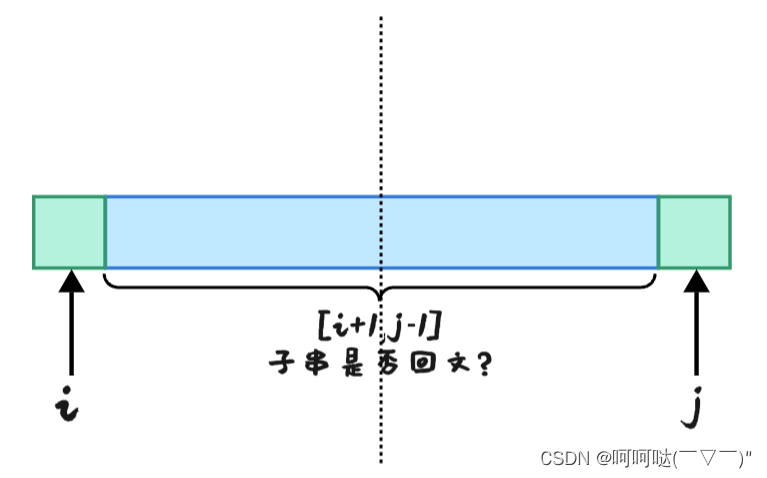
也就是说,如果在[i+1,j-1]范围的子串是一个回文串,再向两边拓展遍历的时候,那只需要判断两边这两个元素是否相同就可以了。若相同,dp[i][j]是回文串。
>>动规五部曲
1.确定dp数组以及下标的含义
- dp[i][j]:表示区间范围[i,j]的子串是否为回文子串。如果是,则dp[i][j] = true,否则为false
- 或者说,dp[i][j] 表示截取从 i 到 j 的子串是否为回文子串
2.确定递推式
if(j == i) dp[i][j]=true;
else if(j-i == 1) dp[i][j] = (s[i]==s[j]);
else dp[i][j] = (s[i] == s[j] && dp[i+1][j-1]);3.dp 数组初始化
- dp[i][j]初始化为false
4.确定遍历顺序
一定要从下到上,从左到右遍历,这样能保证dp[i+1][j-1]是经过计算得来的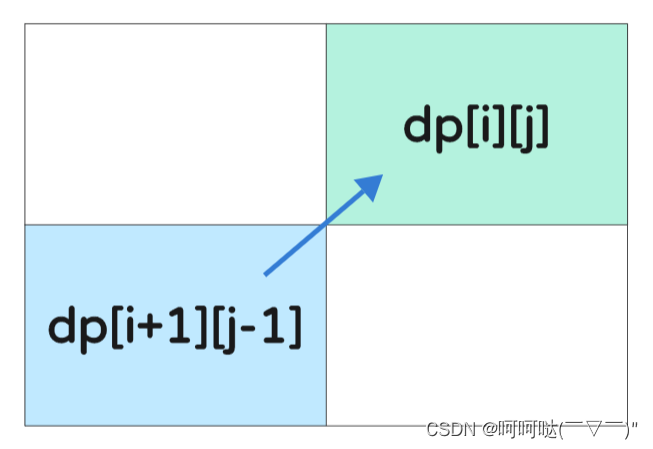
5.举例推导dp数组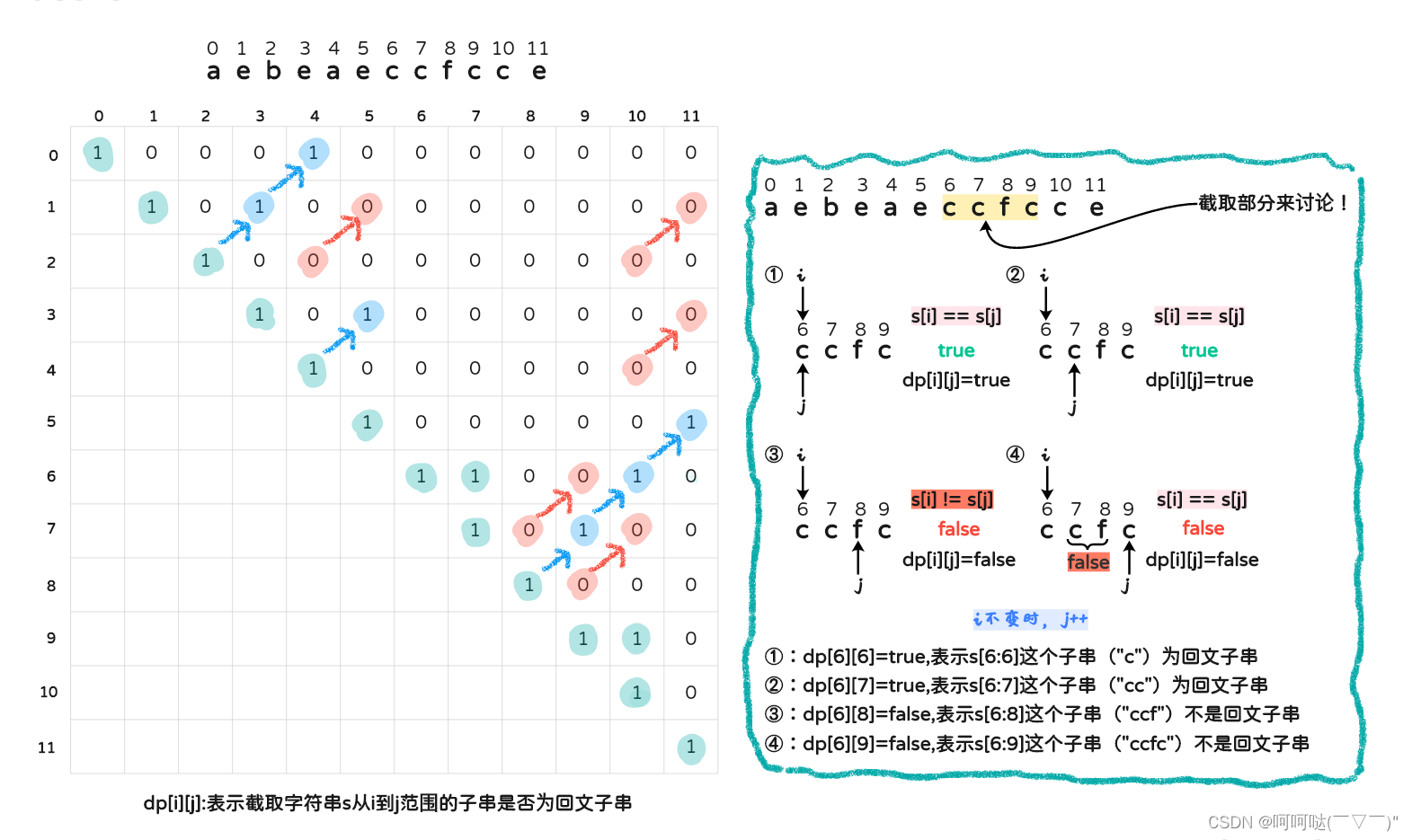
void computePalindrome(const string& s) {// dp[i][j] 代表s[i:j](双边包括)是否是回文子串dp.resize(s.size(),vector<bool>(s.size(),false));// 根据字符串s,刷新布尔矩阵的大小for(int i=s.size()-1;i>=0;i--) {// 需要倒序计算,保证在i行时,i+1行已经计算好了for(int j=i;j<s.size();j++) {if(j == i) dp[i][j]=true;else if(j-i == 1) dp[i][j] = (s[i]==s[j]);else dp[i][j] = (s[i] == s[j] && dp[i+1][j-1]);}}
}"aebeaeccfcce"
1 0 0 0 1 0 0 0 0 0 0 0
0 1 0 1 0 0 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0 0 0 0
0 0 0 1 0 1 0 0 0 0 0 0
0 0 0 0 1 0 0 0 0 0 0 0
0 0 0 0 0 1 0 0 0 0 0 1
0 0 0 0 0 0 1 1 0 0 1 0
0 0 0 0 0 0 0 1 0 1 0 0
0 0 0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 0 0 1 1 0
0 0 0 0 0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 0 0 0 0 1 "acgcabbfcc"
1 0 0 0 1 0 0 0 0 0
0 1 0 1 0 0 0 0 0 0
0 0 1 0 0 0 0 0 0 0
0 0 0 1 0 0 0 0 0 0
0 0 0 0 1 0 0 0 0 0
0 0 0 0 0 1 1 0 0 0
0 0 0 0 0 0 1 0 0 0
0 0 0 0 0 0 0 1 0 0
0 0 0 0 0 0 0 0 1 1
0 0 0 0 0 0 0 0 0 1 (二)分割回文串 + 动态规划 + 回溯算法 + 优化
class Solution {
public:vector<vector<string>> result;vector<string> path; // 放已经回文的子串vector<vector<bool>> dp; // 放事先计算好的是否回文子串的结果void backtracking(const string& s,int startIndex) {// 如果起始位置已经大于 s 的大小,说明已经找到了一组分割方案了if(startIndex >= s.size()) {result.push_back(path);return;}for(int i=startIndex;i<s.size();i++) {if(dp[startIndex][i]) { // 是回文子串// 获取[startIndex,i] 在 s 中的子串string subStr = s.substr(startIndex,i-startIndex+1);path.push_back(subStr);}else continue; // 不是回文,跳过backtracking(s,i+1);// 寻找 i+1 为起始位置的子串path.pop_back();// 回溯过程,弹出本次已经添加的子串}}void computePalindrome(const string& s) {// dp[i][j] 代表s[i:j](双边包括)是否是回文子串dp.resize(s.size(),vector<bool>(s.size(),false));// 根据字符串s,刷新布尔矩阵的大小for(int i=s.size()-1;i>=0;i--) {// 需要倒序计算,保证在i行时,i+1行已经计算好了for(int j=i;j<s.size();j++) {if(j == i) dp[i][j]=true;else if(j-i == 1) dp[i][j] = (s[i]==s[j]);else dp[i][j] = (s[i] == s[j] && dp[i+1][j-1]);}}}vector<vector<string>> partition(string s) {computePalindrome(s);backtracking(s, 0);return result;}
};参考和推荐文章:
代码随想录 (programmercarl.com)![]() https://www.programmercarl.com/0131.%E5%88%86%E5%89%B2%E5%9B%9E%E6%96%87%E4%B8%B2.html#%E6%80%9D%E8%B7%AF
https://www.programmercarl.com/0131.%E5%88%86%E5%89%B2%E5%9B%9E%E6%96%87%E4%B8%B2.html#%E6%80%9D%E8%B7%AF
摘选代码随想录的总结:
- 总结难点:
- 如何切割?切割问题可以抽象为组合问题
- 如何模拟那些切割线?
- 切割问题中递归如何终止?
- 在递归循环中如何截取子串?
- 如何判断回文?
递归用于纵向遍历,for循环用于横向遍历当切割线迭代至字符串末尾,说明找到一种方法。类似组合问题,为了不重复切割同一位置,利用 start_index 作为标记,记录下一轮。递归的起始位置(切割线)。切割过的地方不能重复切割,故递归函数传入 i+1
相关文章:
leetCode 131.分割回文串 + 动态规划 + 回溯算法 + 优化 + 图解 + 笔记
我的往期文章: leetCode 647.回文子串 动态规划 优化空间 / 中心扩展法 双指针-CSDN博客https://blog.csdn.net/weixin_41987016/article/details/133883091?spm1001.2014.3001.5501leetCode 131.分割回文串 回溯算法 图解 笔记-CSDN博客https://blog.csdn.n…...
【傻瓜级JS-DLL-WINCC-PLC交互】3.JS-DLL进行交互
思路 JS-DLL-WINCC-PLC之间进行交互,思路,先用Visual Studio创建一个C#的DLL控件,然后这个控件里面嵌入浏览器组件,实现JS与DLL通信,然后DLL放入到WINCC里面的图形编辑器中,实现DLL与WINCC的通信。然后PLC与…...

深度学习手势识别算法实现 - opencv python 计算机竞赛
文章目录 1 前言2 项目背景3 任务描述4 环境搭配5 项目实现5.1 准备数据5.2 构建网络5.3 开始训练5.4 模型评估 6 识别效果7 最后 1 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 深度学习手势识别算法实现 - opencv python 该项目较为新颖…...

2023-12-01 AIGC-自动生成ppt的AI工具
摘要: 2023-12-01 AIGC-自动生成ppt-记录 自动生成ppt: BoardMix boardmix 一键生成ppt boardmix是一款基于云的ai设计软件,允许创建用于各种目的的自定义演示文稿、ai绘画,ai生成思维导图等。以下是它的一些功能: 可定制的模板 - 它有一个…...
NoSQL 数据建模错误会降低性能
数据建模错误是破坏性能的最简单方法之一。当您使用 NoSQL 时,特别容易搞砸,(讽刺的是)NoSQL 往往用于对性能最敏感的工作负载。NoSQL 数据建模最初可能看起来非常简单:只需对数据进行建模以适应应用程序的访问模式。但…...
在Android上搭建一个NDK项目
首先New Project,选择Native C,点击Next。 填入项目名称和包名,点击Next。 这里我们选择Cmake默认的C版本。 创建好的项目目录,里面比我们正常的Android项目多了一个cpp目录 打开MainActivity。里面定义了一个jni方法stringFromJN…...
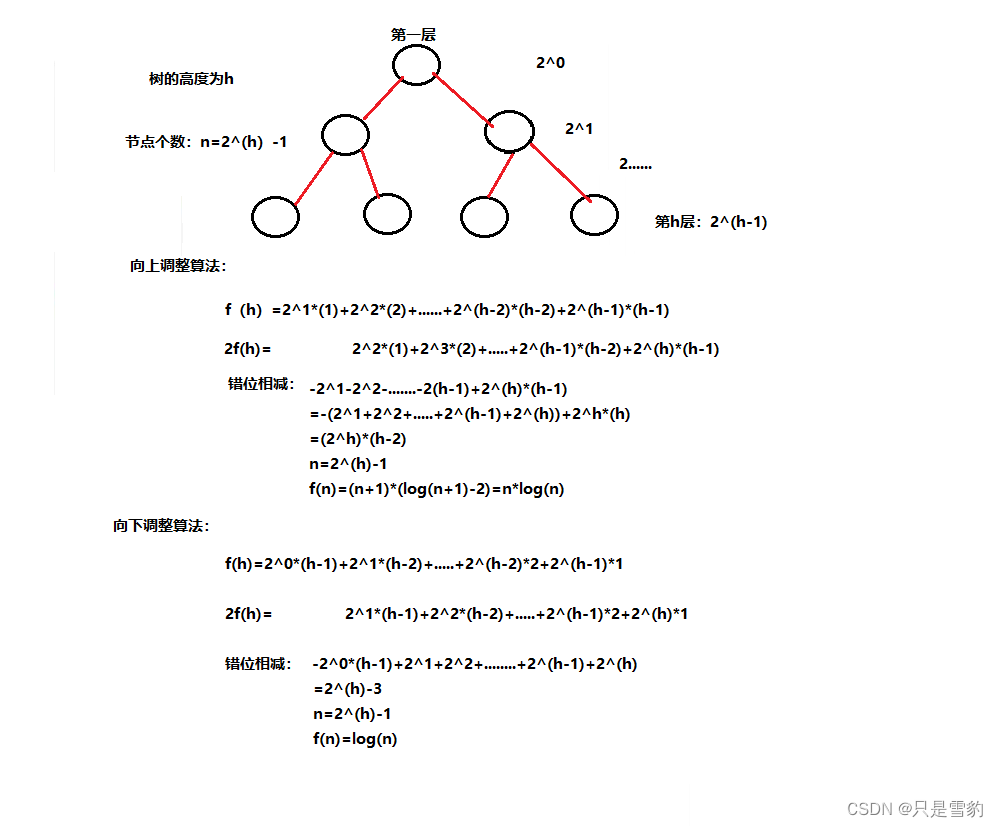
TOP-K问题和向上调整算法和向下调整算法的时间复杂度问题的分析
TOP-K问题 TOP-K问题:即求数据结合中前K个最大的元素或者最小的元素,一般情况下数据量都比较大 比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等 对于Top-K问题,能想到的最简单直接的方式就是排序,但是…...

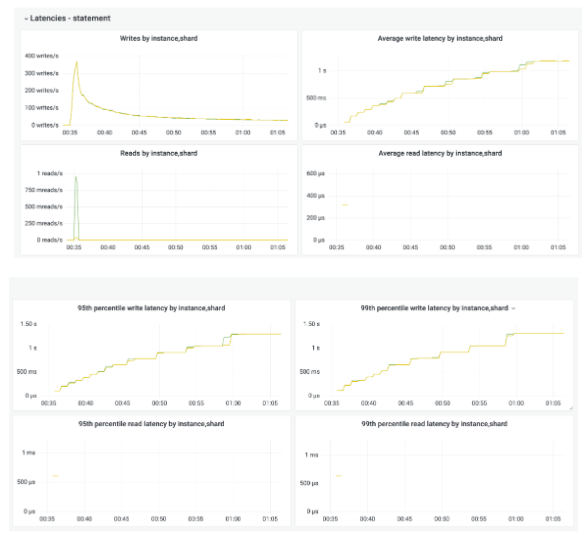
3、服务器性能剖析
性能优化简介 **我们将性能定义为完成某件任务所需要的时间度量,换句话说,性能即响应时间,这是一个非常重要的原则。**我们通过任务和时间而不是资源来测量性能。数据库服务器的目的是执行sql语句,所以他关注的任务是查询或者语句…...

xxl-job 分布式任务调度框架
文章目录 分布式任务调度XXL-Job 简介XXL-Job 环境搭建XXL-Job (源码说明)配置部署调度中心docker安装 Bean模式任务(方法形式)-入门案例任务详解任务详解-执行器任务详解-基础配置任务详解-调度配置任务详解-基础配置任务详解-阻塞处理策略任务详解-路由策略 路由策略路由策略…...

软件使用-stm32入门
这节主要是介绍大家使用两个软件。这两个软件也是比较常用的,里面也有很多有意思的功能,可以给大家介绍一下。 1. FlyMcu 软件 这个软件可以通过串口给 STM32 下载程序,如果你没有 STLINK,就可以用这个软件通过串口下载程序。 …...
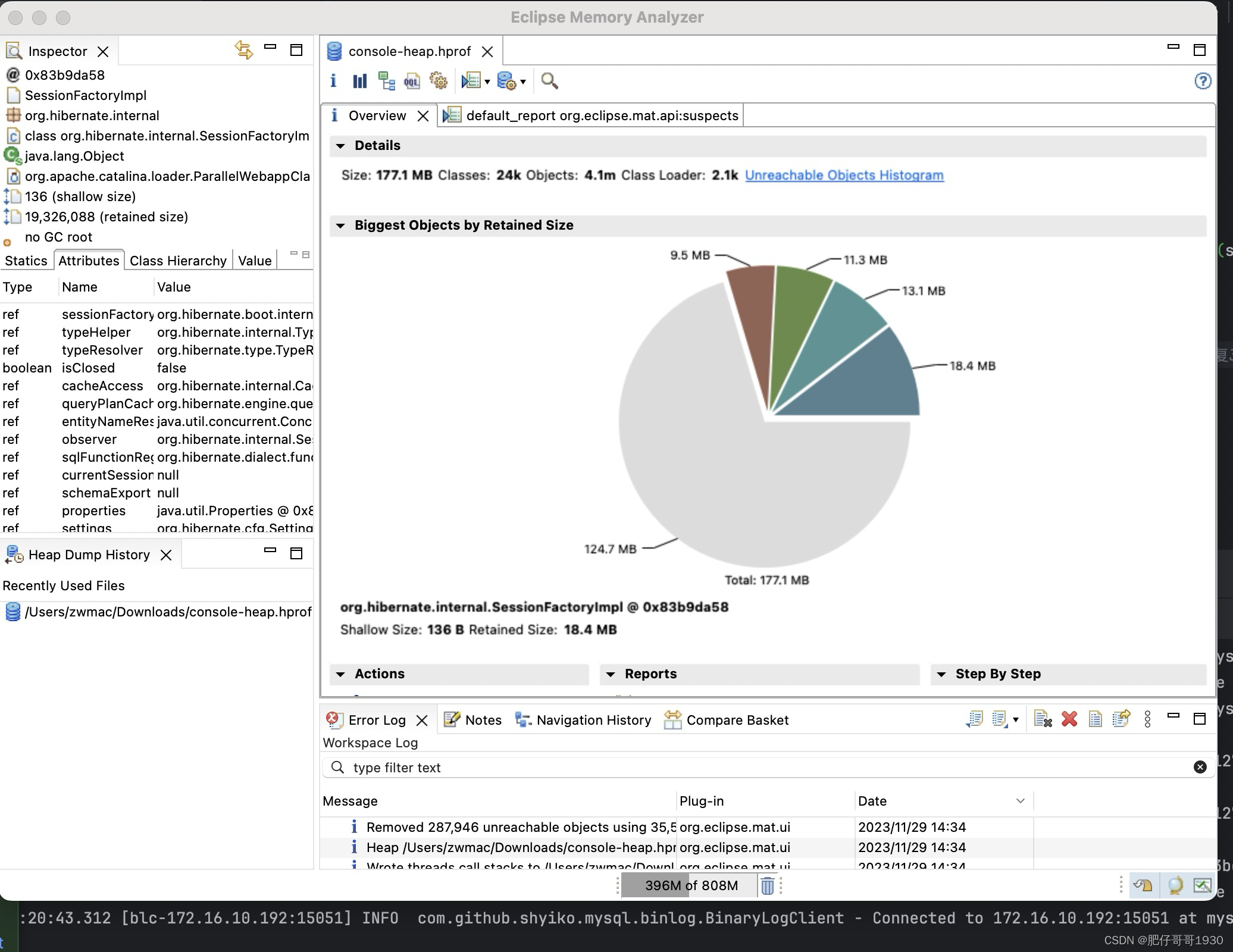
使用MAT分析内存泄漏(mac)
前言 今天主要简单分享下Eclipse的Memory Analyzer在mac下的使用。 一、Mat(简称)干什么的? 就是分析java内存泄漏的工具。 二、使用步骤 1.下载 mac版的现在也分芯片,别下错了。我这里是M2芯片的,下载的Arch64的。 …...
【Vue】Linux 运行 npm run serve 报错 vue-cli-service: Permission denied
问题描述 在Linux系统上运行npm run serve命令时,控制台报错: sudo npm run serve project50.1.0 serve vue-cli-service serve sh: 1: vue-cli-service: Permission denied错误截图如下: 原因分析 该错误是由于vue-cli-service文件权限不…...
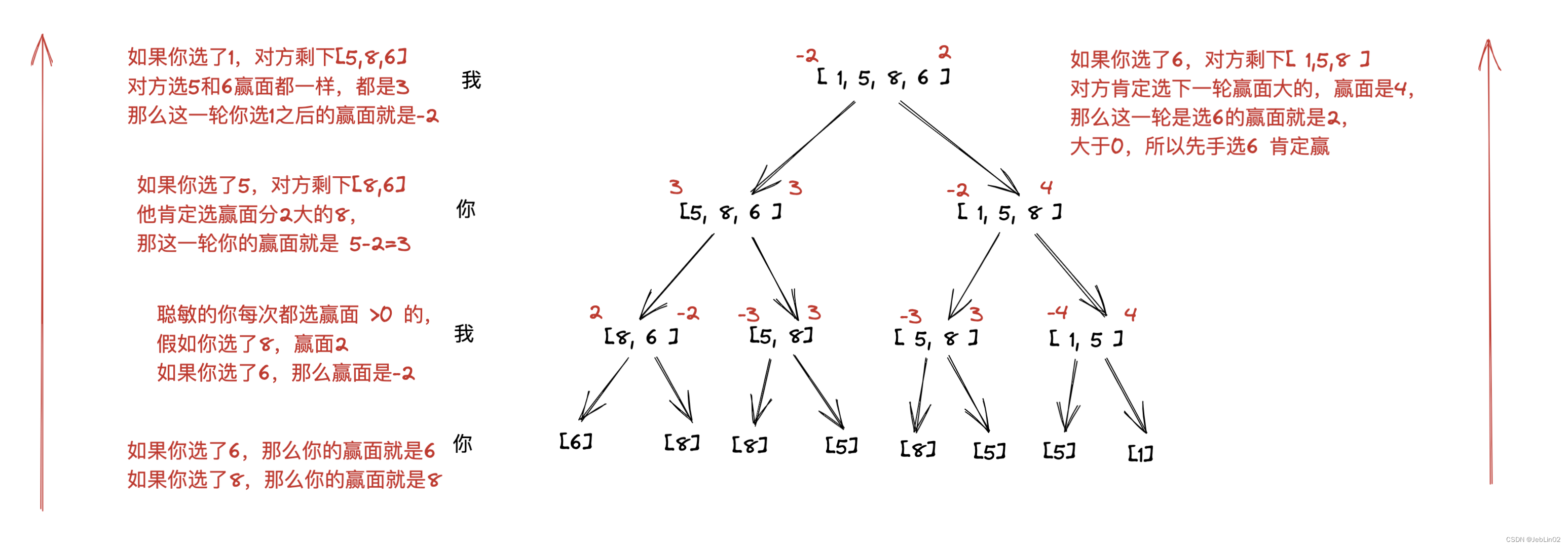
LeetCode的几道题
一、捡石头 292 思路就是: 谁面对4块石头的时候,谁就输(因为每次就是1-3块石头,如果剩下4块石头,你怎么拿,我都能把剩下的拿走,所以你就要想尽办法让对面面对4块石头的倍数, 比如有…...

NLP/Natural Language Processing
一、NLP是什么 自然语言处理( Natural Language Processing, NLP)是计算机科学领域与人工智能领域中的一个重要方向,也就是人们常说的「自然语言处理」,就是研究如何让计算机读懂人类语言,即将人的自然语言转换为计算机可以阅读的指令。它研…...
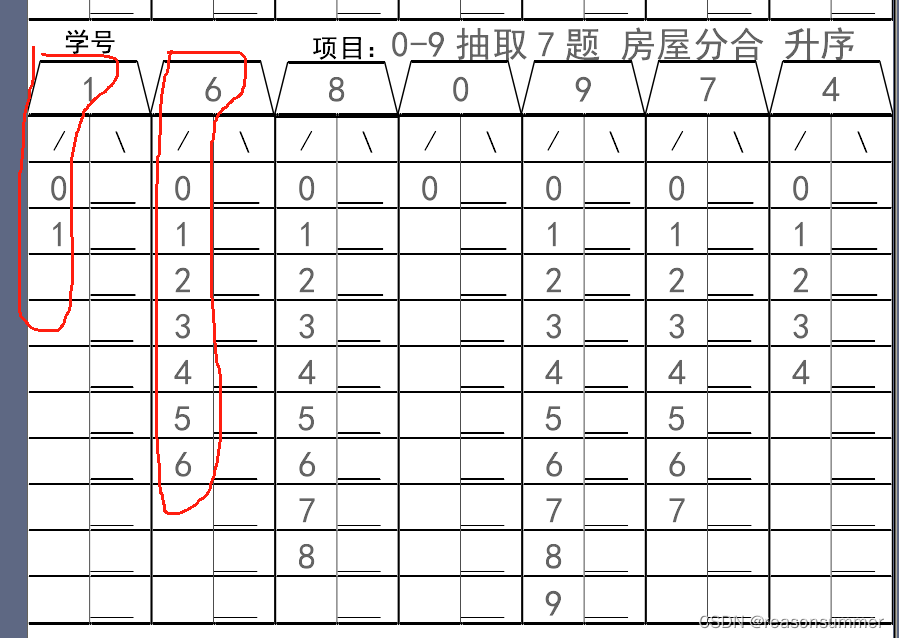
【教学类-06-12】20231202 0-9数字分合-房屋样式(一)-下右空-升序-抽7题
作品展示-屋顶分合(0-9之间随机抽取7个不重复分合) 背景需求: 大班幼儿学分合题,通常区角里会设计一个“房屋分合”的样式 根据这种房屋样式,设计0-9内的升序分合题模板 素材准备 WORD样式 代码展示: 2-9…...
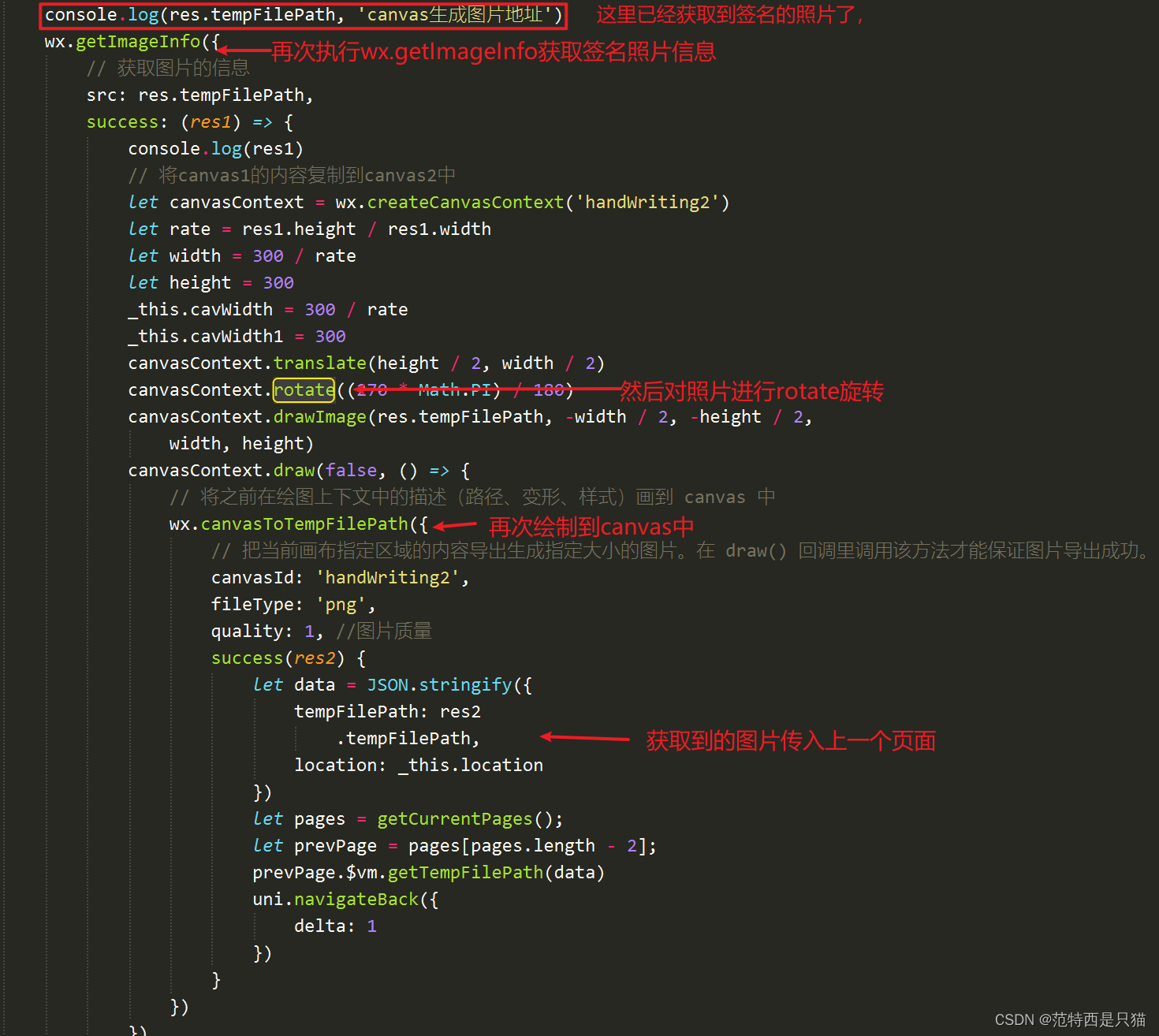
uni-app 微信小程序 电子签名及签名图片翻转显示功能
文章目录 1. 需求背景2. 开始撸2.1 点击 重写 进入签名页面(上图一)2.2 书写签名,点击确认返回,及图片翻转显示(上图二,三) 3. 图片进行翻转,返回翻转后的图片 1. 需求背景 接的一个…...

MySQL 8.0关键字和保留字
官网地址: https://dev.mysql.com/doc/refman/8.0/en/keywords.html 可以粘贴出去自己排版整理 {accessible} {account} {action} {active} {add} {admin} {after} {against} {aggregate} {algorithm} {all} {alter} {always} {analyse} {analyze} …...

PyLMKit(3):基于角色扮演的应用案例
角色扮演应用案例RolePlay 0.项目信息 日期: 2023-12-2作者:小知课题: 通过设置角色模板并结合在线搜索、记忆和知识库功能,实现典型的对话应用功能。这个功能是大模型应用的基础功能,在后续其它RAG等功能中都会用到这个功能。功…...

JAVA全栈开发 集合详解(day14+day15汇总)
一、数组 数组是一个容器,可以存入相同类型的多个数据元素。 数组局限性: 长度固定:(添加–扩容, 删除-缩容) 类型是一致的 对象数组 : int[] arr new int[5]; … Student[] arr …...
Linux Spug自动化运维平台本地部署与公网远程访问
文章目录 前言1. Docker安装Spug2 . 本地访问测试3. Linux 安装cpolar4. 配置Spug公网访问地址5. 公网远程访问Spug管理界面6. 固定Spug公网地址 前言 Spug 面向中小型企业设计的轻量级无 Agent 的自动化运维平台,整合了主机管理、主机批量执行、主机在线终端、文件…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...
