深度学习常见回归分支算法逐步分析,各种回归之间的优缺点,适用场景,举例演示
文章目录
- 1、线性回归(Linear Regression)
- 1.1 优点
- 1.2 缺点
- 1.3 适用场景
- 1.4 图例说明
- 2、多项式回归(Polynomial Regression)
- 2.1 优点
- 2.2 缺点
- 2.3 适用场景
- 2.4 图例说明
- 3、决策树回归(Decision Tree Regression)
- 3.1 优点
- 3.2 缺点
- 3.3 适用场景
- 4、随机森林回归(Random Forest Regression)
- 4.1 优点
- 4.2 缺点
- 4.3 适用场景
- 5、逻辑斯蒂回归(Logistic Regression)
- 5.1 优点
- 5.2 缺点
- 5.3 适用场景
- 6、弹性网络回归(Elastic Net Regression)
- 6.1 优点
- 6.2 缺点
- 6.3 适用场景
- 7、岭回归(Ridge Regression)
- 7.1 优点
- 7.2 缺点
- 7.3 适用场景
- 8、Lasso回归(Lasso Regression)
- 8.1 优点
- 8.2 缺点
- 8.3 适用场景
回归的概念:回归算法是一种用于预测连续数值输出的监督学习算法,可以根据输入特征预测一个或多个目标变量。它有多个分支,每个分支都有其独特的优缺点。下面是深度学习中几类回归变种:
1、线性回归(Linear Regression)
线性回归算法可以说是回归算法里面最简单的一种。
1.1 优点
- 简单且易于解释。
- 计算效率高,适用于大规模数据集。
- 在特征与目标之间存在线性关系时效果良好。
1.2 缺点
- 无法处理非线性关系。对于一些异常值,无法做到拟合曲线。
- 对异常值敏感。
- 需要满足线性回归假设(如线性关系、残差正态分布等)。
1.3 适用场景
适用场景:预测数值型目标,建立输入特征和输出之间的线性关系。
案例:预测房价。根据房屋特征(面积、卧室数量等),建立线性关系来估计房价。
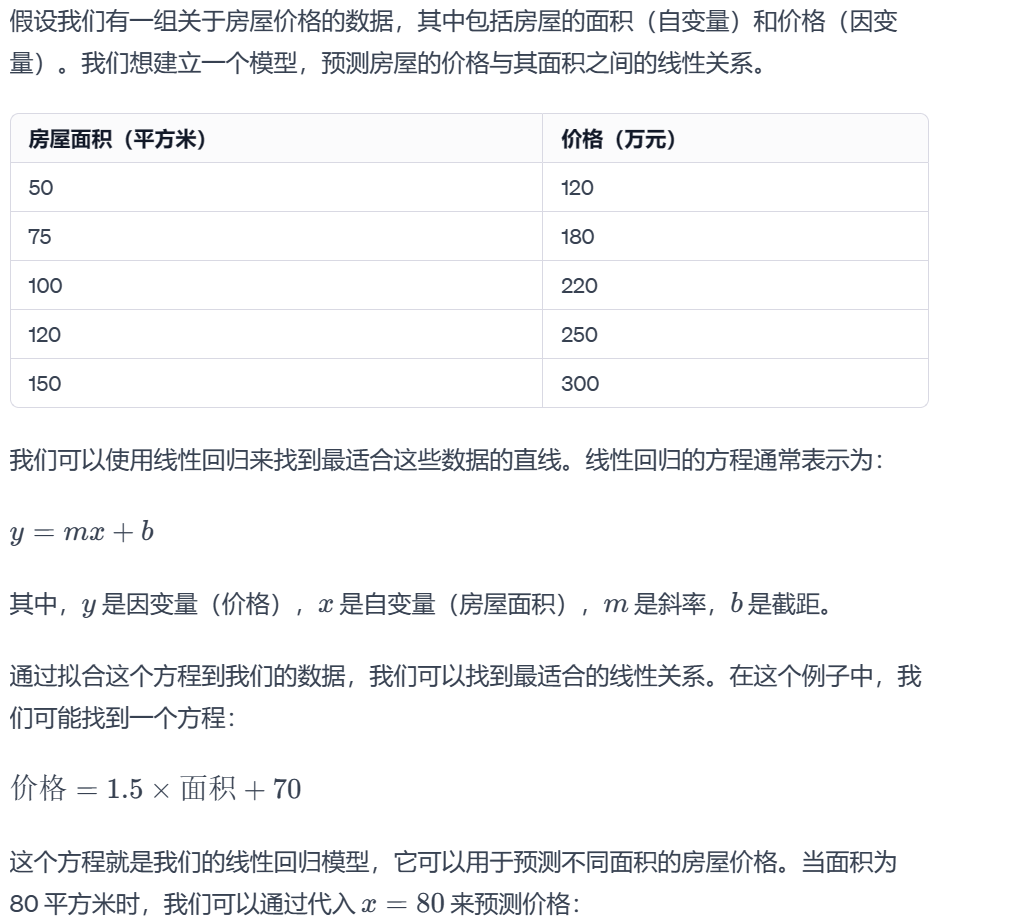

1.4 图例说明
代码:
import matplotlib.pyplot as plt
import numpy as np# 设置中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False# 数据
area = np.array([50, 75, 100, 120, 150])
price = np.array([120, 180, 220, 250, 300])# 执行线性回归
coefficients = np.polyfit(area, price, 1)
m, b = coefficients# 创建预测模型
predict_model = np.poly1d(coefficients)# 生成预测值
predicted_price = predict_model(area)# 绘制原始数据点
plt.scatter(area, price, label='实际数据点')# 绘制线性回归线
plt.plot(area, predicted_price, label=f'线性回归: y = {m:.2f}x + {b:.2f}', color='red')# 添加标签和图例
plt.xlabel('房屋面积(平方米)')
plt.ylabel('价格(万元)')
plt.title('线性回归')
plt.legend()
# 显示图形
plt.show()
生成对应图像:

深度学习中的线性回归
代码:
import torch
import torch.nn as nn
import torch.optim as optim
import numpy as np
import matplotlib.pyplot as plt# 设置中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False# 生成模拟数据
np.random.seed(42)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)# 转换为PyTorch的Tensor
X_tensor = torch.from_numpy(X).float()
y_tensor = torch.from_numpy(y).float()# 定义线性回归模型
class LinearRegressionModel(nn.Module):def __init__(self, input_size, output_size):super(LinearRegressionModel, self).__init__()self.linear = nn.Linear(input_size, output_size)def forward(self, x):return self.linear(x)# 实例化模型
input_size = 1
output_size = 1
model = LinearRegressionModel(input_size, output_size)# 定义损失函数和优化器
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)# 训练模型
num_epochs = 100
for epoch in range(num_epochs):# Forward passoutputs = model(X_tensor)loss = criterion(outputs, y_tensor)# Backward pass and optimizationoptimizer.zero_grad()loss.backward()optimizer.step()# 打印训练过程中的损失if (epoch+1) % 10 == 0:print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item():.4f}')# 绘制模型预测结果和真实数据
predicted = model(X_tensor).detach().numpy()
plt.scatter(X, y, label='实际数据点')
plt.plot(X, predicted, label='模型预测', color='red')
plt.xlabel('房屋面积(平方米)')
plt.ylabel('价格(万元)')
plt.title('线性回归')
plt.legend()
plt.show()
生成对应的图像:

是不是看着比简单的回归复杂很多,深度模型解决的回归问题还要比这复杂得多。
2、多项式回归(Polynomial Regression)
2.1 优点
- 可以捕捉特征和目标之间的非线性关系。
- 相对简单实现。
2.2 缺点
- 可能会过度拟合数据,特别是高阶多项式。
- 需要选择适当的多项式阶数。
2.3 适用场景
适用场景:处理非线性关系,通过添加多项式特征来拟合曲线。
案例:预测股票价格。使用多项式回归来拟合价格与时间之间的非线性关系。
2.4 图例说明
代码:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures
from sklearn.metrics import mean_squared_error# 设置中文显示
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False# 生成模拟数据
np.random.seed(42)
X = 2 * np.random.rand(100, 1)
y = 4 + 3 * X + np.random.randn(100, 1)# 选择多项式次数
degree = 2# 构建设计矩阵
poly_features = PolynomialFeatures(degree=degree, include_bias=False)
X_poly = poly_features.fit_transform(X)# 使用线性回归拟合多项式特征
lin_reg = LinearRegression()
lin_reg.fit(X_poly, y)# 预测
X_new = np.linspace(0, 2, 100).reshape(-1, 1)
X_new_poly = poly_features.transform(X_new)
y_new = lin_reg.predict(X_new_poly)# 绘制结果
plt.scatter(X, y, label='True data')
plt.plot(X_new, y_new, 'r-', label='Predictions', linewidth=2)
plt.xlabel('X')
plt.ylabel('y')
plt.title('多项式线性回归')
plt.legend()
plt.show()# 评估模型
y_pred = lin_reg.predict(X_poly)
mse = mean_squared_error(y, y_pred)
print(f'Mean Squared Error: {mse:.4f}')
生成对应图像:

3、决策树回归(Decision Tree Regression)
3.1 优点
- 能够处理非线性关系。
- 不需要对数据进行特征缩放。
- 结果易于可视化和解释。
3.2 缺点
- 容易过拟合。树越深,越可能发生过拟合现象。
- 对数据中的噪声敏感。
- 不稳定,小的数据变化可能导致不同的树结构。
3.3 适用场景
适用场景:适用于非线性数据,创建树状结构进行回归预测。
案例:天气预测。基于多个天气因素,预测温度。
4、随机森林回归(Random Forest Regression)
4.1 优点
- 降低了决策树回归的过拟合风险。
- 能够处理高维数据。
4.2 缺点
- 失去了部分可解释性。
- 难以调整模型参数。
4.3 适用场景
适用场景:用于回归任务,具有高度的鲁棒性。
案例:股票价格预测。使用多个随机森林树来预测未来的股票价格。
5、逻辑斯蒂回归(Logistic Regression)
5.1 优点
- 用于二分类问题,广泛应用于分类任务。
- 输出结果可以解释为概率。
5.2 缺点
- 仅适用于二分类问题。这是它的优点,也是它的缺点。
- 对于复杂的非线性问题效果可能不佳。对线性问题解答较好。
5.3 适用场景
适用场景:用于二分类或多分类任务,预测概率分布。
案例:垃圾邮件分类。根据邮件内容来判断是否是垃圾邮件。
6、弹性网络回归(Elastic Net Regression)
6.1 优点
- 综合了岭回归和Lasso回归的优点。
- 可以应对多重共线性和特征选择。
6.2 缺点
- 需要调整两个正则化参数。
6.3 适用场景
适用场景:结合了 Ridge 和 Lasso 的优点,适用于高维数据和特征选择。
案例:医学诊断。处理具有大量特征的患者数据,选择最相关的特征。
7、岭回归(Ridge Regression)
7.1 优点
- 可以解决多重共线性问题。
- 对异常值不敏感。
7.2 缺点
- 不适用于特征选择,所有特征都会被考虑。
- 参数需要调整。
7.3 适用场景
适用场景:处理多重共线性问题,添加L2正则化以防止过拟合。
案例:预测学生成绩。处理多个高度相关的特征,如学习时间、家庭支持等。
8、Lasso回归(Lasso Regression)
8.1 优点
- 可以用于特征选择,趋向于将不重要的特征的系数推到零。
- 可以解决多重共线性问题。
8.2 缺点
- 对于高维数据,可能会选择较少的特征。
- 需要调整正则化参数。
8.3 适用场景
适用场景:用于特征选择和稀疏性,通过L1正则化将一些特征的权重设为零。
案例:预测产品销量。确定哪些产品特征对销售额的影响最大。
相关文章:

深度学习常见回归分支算法逐步分析,各种回归之间的优缺点,适用场景,举例演示
文章目录 1、线性回归(Linear Regression)1.1 优点1.2 缺点1.3 适用场景1.4 图例说明 2、多项式回归(Polynomial Regression)2.1 优点2.2 缺点2.3 适用场景2.4 图例说明 3、决策树回归(Decision Tree Regression&#…...
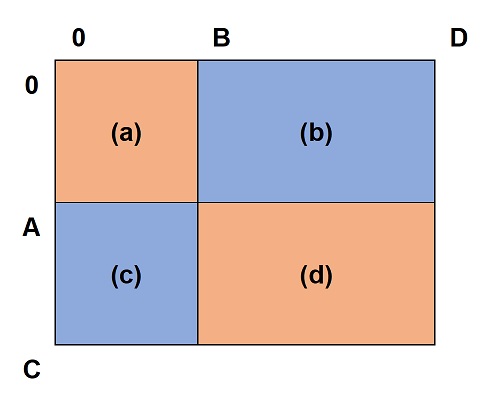
Programming Contest 2023(AtCoder Beginner Contest 331)D题 Tile Pattern --- 题解
目录 D - Tile Pattern 题目大意: 思路: 代码: D - Tile Pattern D - Tile Pattern (atcoder.jp) 题目大意: 给你一个n和q,n为局部棋盘大小(n*n) 并且给出局部棋盘中黑白子位置的放置情况,q为查询次数…...

Google测试框架googletest简介与使用方法
环境准备(Ubuntu) 下载 git clone https://github.com/google/googletest.git 安装 cd googletest // 创建build目录 mkdir build cd build //编译安装 cmake .. make sudo make install 检查是否安装成功 ls /usr/local/lib// 存在以下文件则说明…...

进程的创建:fork()
引入 创建进程的方式我们已经学习了一个!在我们运行指令(或者运行我们自己写的可执行程序)的时候不就是创建了一个进程嘛?那个创建进程的方式称为指令级别的创建子进程! 那如果我们想要在代码中创建进程该怎么办呢? fork() for…...

Fabric:创建应用通道
搭建自定义网络可以参考文章: https://blog.csdn.net/yeshang_lady/article/details/134113296 1 创建通道 网络搭建完成之后,就可以开始创建通道了。Fabric V2.5.4中可以在不创建系统通道的情况下直接创建应用通道。 1.1 修改配置文件 先创建配置文…...
力扣每日一题(2023-11-30)
力扣每日一题 题目:1657. 确定两个字符串是否接近 日期:2023-11-30 用时:21 m 07 s 时间:11ms 内存:43.70MB 代码: class Solution {public boolean closeStrings(String word1, String word2) {if(word1.…...
内部类Lambda
静态内部类 /*** 静态成员是在类加载成字节码时就已经存在的,静态只能访问静态*/ public class Demo {public static void main(String[] args) {Outer.Inner.show();} }class Outer {int num1 10;static int num2 20;static class Inner {static void show() {Outer outer …...

设一棵二叉树中各结点的值互不相同,其先序遍历序列和中序遍历序列分别存于两个一维数组A[1...n]和 Bfl...n]中,试编写算法建立该二叉树的二叉链表。
题目描述:设一棵二叉树中各结点的值互不相同,其先序遍历序列和中序遍历序列分别存于两个一维数组A[1…n]和 B[1…n]中,试编写算法建立该二叉树的二叉链表。 分析: 对于一颗二叉树,知道其中序和先序序列就可以完全确定…...

什么是Daily Scrum?
Daily Scrum(每日站会),Scrum Master要确保这个会在每天都会开。这个会的目的就是检查正在做的东西和方式是否有利于完成Sprint目的,并及时做出必要的调整。 每日站会一般只开15分钟,为了让事情更简单些,这…...

逆波兰表达式求值[中等]
优质博文:IT-BLOG-CN 一、题目 给你一个字符串数组tokens,表示一个根据 逆波兰表示法 表示的算术表达式。请你计算该表达式。返回一个表示表达式值的整数。 有效的算符为 ‘’、‘-’、‘*’ 和 ‘/’ 。 每个操作数(运算对象)都…...

Oracle连接和使用
5. Oracle连接和使用 5.1. sqlplus sqlplus作为甲骨文公司提供的一款本族工具产品,有着悠久的历史和积淀,它几乎伴随着Oracle数据库产生至今的整个生命周期,而且,还会继续和Oracle数据库产品相伴一直发展下去。该工具看似简单灵活的背后,却为广大用户使用Oracle数据库提…...

redis单线程为什么这么快
redis单线程为什么这么快 redis是使用的单线程来进行操作的,因为所有的数据都是在内存中的,内存操作特别快。而且单线程避免了多线程切换性能损耗问题 单线程如何处理并发客户端连接? redis利用epoll来实现IO多路复用,将连接信息和…...
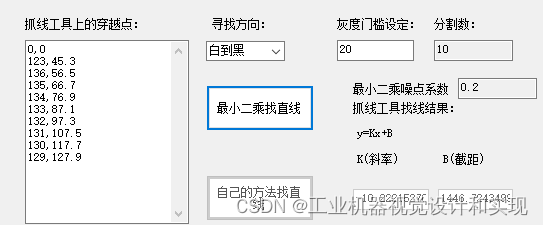
工业机器视觉megauging(向光有光)使用说明书(五,轻量级的visionpro)
这个说明主要介绍抓线功能。 第一步,添加线工具,鼠标双击工具箱“抓线”,出现如下界面: 第二步,我们拉一条,“九点标定”到“抓线1”的线,和visionpro操作一样: 第三步,…...

【LittleXi】2023年广东工业大学腾讯杯新生程序设计竞赛
文章目录 【LittleXi】2023年广东工业大学腾讯杯新生程序设计竞赛A.星期几考试?C.信件D、乘除法E、不知道叫什么名字F.我要学会盾反!G.闪闪发光心动不已!H.不想想背景的gcdI.uu爱玩飞行棋J.火柴人小游戏K .有趣的BOSS 【LittleXi】2023年广东…...

【C语言:数据在内存中的存储】
文章目录 1.整数在内存中的存储1.1整数在内存中的存储1.2整型提升 2.大小端字节序2.1什么是大小端2.2为什么有大小端之分 3.整数在内存中的存储相关题目题目一题目二题目三题目四题目五题目六题目七 4.浮点数在内存中的存储4.1浮点数存的过程4.2浮点数取得过程 在这之前呢&…...

每日一练:阿姆斯特朗数
如果一个 n 位正整数等于其各位数字的 n 次方之和,则称该数为阿姆斯特朗数。 例如 1^3 5^3 3^3 153。 1000 以内的阿姆斯特朗数: 1, 2, 3, 4, 5, 6, 7, 8, 9, 153, 370, 371, 407。...
)
fatal: remote error: upload-pack: not our ref (未解决问题)
PX4使用 git submodule update --init --recursive报错 fatal: remote error: upload-pack: not our ref解决办法参考:https://stackoverflow.com/questions/61163082/why-does-git-submodule-update-fail-with-fatal-remote-error-upload-pack-not-o 感觉就是清…...
、readline()、readlines() 函数 读取文件)
Python 3 使用 read()、readline()、readlines() 函数 读取文件
1 样例文件 example.txt 春晓 孟浩然〔唐代〕 春眠不觉晓,处处闻啼鸟。 夜来风雨声,花落知多少。 2 分别使用 read()、readline()、readlines() 函数 2.1 # read() -------- 一次性读取所有文本,以字符串的形式返回结果。 # read() ----…...
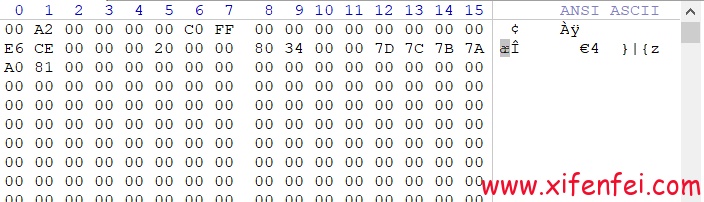
勒索解密后oracle无法启动故障处理----惜分飞
客户linux平台被勒索病毒加密,其中有oracle数据库.客户联系黑客进行解密【勒索解密oracle失败】,但是数据库无法正常启动,dbv检查数据库文件报错 [oraclehisdb ~]$ dbv filesystem01.dbf DBVERIFY: Release 11.2.0.1.0 - Production on 星期一 11月 27 21:49:17 2023 Copyrig…...
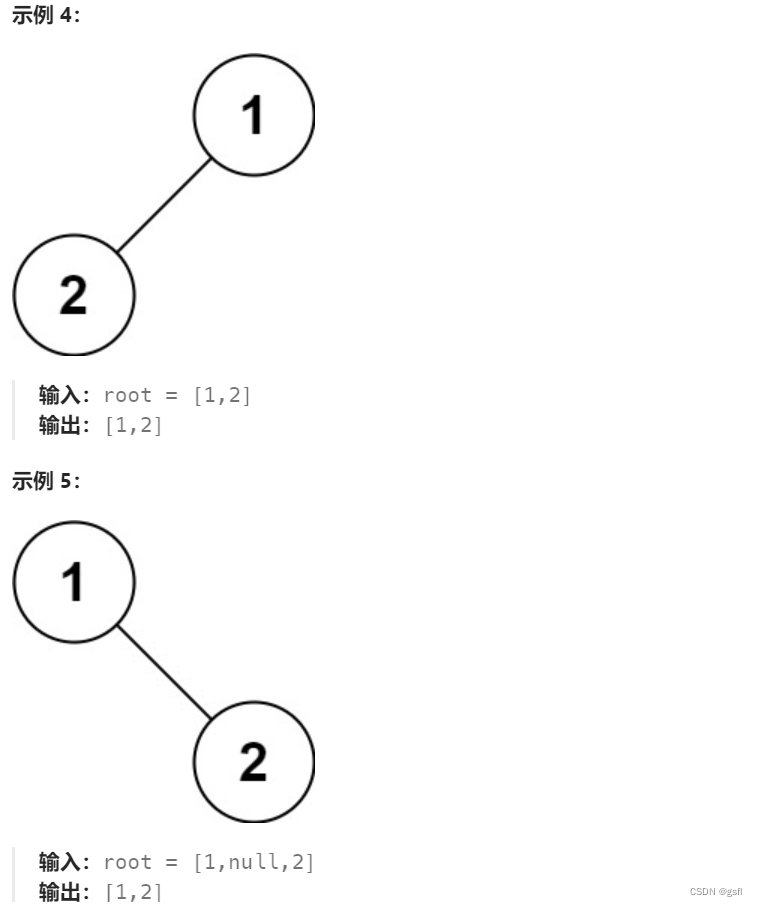
Leetcode144. 二叉树的前序遍历-C语言
文章目录 题目介绍题目分析解题思路1.创建一个数组来储存二叉树节点的值2.根据二叉树的大小来开辟数组的大小3.边前序遍历边向创建的数组中存入二叉树节点的值 完整代码 题目介绍 题目分析 题目要求我们输出二叉树按前序遍历排列的每个节点的值。 解题思路 1.创建一个数组来…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

Monorepo架构: Nx Cloud 扩展能力与缓存加速
借助 Nx Cloud 实现项目协同与加速构建 1 ) 缓存工作原理分析 在了解了本地缓存和远程缓存之后,我们来探究缓存是如何工作的。以计算文件的哈希串为例,若后续运行任务时文件哈希串未变,系统会直接使用对应的输出和制品文件。 2 …...
