.NET8构建统计Extreme Optimization Numerical Libraries
为 .NET 8 构建统计应用程序
Extreme Optimization Numerical Libraries for .NET 是通用数学和统计类的集合,为技术和统计计算提供了完整的平台。它将数学库、向量和矩阵库以及统计库结合在一个方便的包中。它包括对线性代数、复数、数值积分和微分、求解方程、优化、随机数、回归、方差分析、统计分布和假设检验的支持。
Numerical Libraries for .NET V8.1.22 增加了对 .NET 8 的支持,允许开发人员在 Microsoft 流行的 .NET 生态系统的新版本中构建金融、工程和科学应用程序。
关于 .NET 的极限优化数值库
构建金融、工程和科学应用程序。
Extreme Optimization Numerical Libraries for .NET 是通用数学和统计类的集合。它为基于 Microsoft .NET 平台构建的技术和统计计算提供了一个完整的平台。它将数学库、向量和矩阵库以及统计库结合在一个方便的包中。
一般特征
- 即使对数学不太感兴趣的人也很容易使用。
- 通过最佳算法的优化实现实现出色的性能。
- 功能强大,足以满足最苛刻的高级用户的需求。
- 直观的对象模型。.NET 极端优化数值库中的对象以及它们之间的关系符合我们的日常概念。
数学库功能
- 一般的
- 机器浮点常量。
- 常见的数学常数。
- 扩展初等函数。
- 算法支持功能:迭代、容错、收敛测试。
- 复数
- 双精度复数值类型。
- 所有算术运算的重载运算符。
- 不支持运算符重载的语言的静态运算符函数。
- 将 System.Math 中的函数扩展到复杂参数。
- 支持复数无穷大和复数非数字 (NaN)。
- 复杂的向量和矩阵类。
- 数值积分与微分
- 数值微分。
- 使用辛普森规则和隆伯格方法进行数值积分。
- 非自适应高斯-克朗罗德数值积分器。
- 自适应高斯-克朗罗德数值积分器。
- 无限间隔积分。
- 具有奇点和/或不连续性的函数的优化。
- 六种集成规则可供选择,或提供您自己的规则。
- 二维或更多维度的积分。
- 曲线拟合和插值
- 使用多项式、三次样条、分段常数和线性曲线进行插值。
- 使用多项式或任意函数进行线性最小二乘拟合。
- 使用预定义函数或您自己的函数进行非线性最小二乘。
- 预定义的非线性曲线:指数、有理、高斯、洛伦兹、4 和 5 参数逻辑。
- 加权最小二乘法,具有 4 个预定义的权重函数。
- 曲线参数的缩放。
- 曲线参数的约束。
- 曲线
- 使用数学曲线的面向对象方法。
- 方法:求值、导数、定积分、正切、求根。
- 许多基本类型的曲线:常数、直线、二次曲线、多项式、三次样条、切比雪夫近似、任意函数的线性组合。
- 解方程
- 多项式的实根和复根。
- 任意函数的根:二分法、误报法、Dekker-Brent 法和 Newton-Raphson 法。
- 联立线性方程组。
- 非线性方程组:鲍威尔混合“狗腿”法、牛顿法。
- 最小二乘解。
- 优化
- 一维优化:布伦特算法,黄金分割搜索。
- N 维拟牛顿法:BFGS 和 DFP 变体。
- N 维共轭梯度法:Fletcher-Reeves 和 Polak-Ribière 变体。
- 鲍威尔共轭梯度法。
- Nelder 和 Mead 的下坡单纯形法。
- Levenberg-Marquardt 非线性最小二乘法。
- 线搜索算法:Moré-Thuente、二次、单位。
- 线性程序求解器:基于修订的单纯形法。
- 线性程序求解器:从 MPS 文件导入。
- 信号处理
- 真正的一维和二维快速傅里叶变换。
- 复杂的二维快速傅里叶变换。
- 因子 2、3、4、5 的特殊代码。
- 实数和复数卷积。
- 托管、32 位和 64 位本机实现。
- 特殊功能
- 标准 .NET Framework 类库中未包含 40 多个特殊函数。
- 组合函数:阶乘、组合、变体等等。
- 数论函数:最大公约数、最小公倍数、质因数分解、素性测试。
- Gamma 及相关函数,包括不完全和正则化 gamma 函数、digamma 函数、beta 函数、调和数。
- 实数和复数的双曲和反双曲函数。
- 第一类和第二类普通贝塞尔函数和修正贝塞尔函数。
- 艾里函数及其导数。
- 指数积分、正弦余弦积分、对数积分。
矢量和矩阵库功能
- 一般的
- 单精度、双精度或四精度实数或复数分量。
- 基于标准 BLAS 和 LAPACK 例程。
- 100% 托管实施,确保安全性、便携性和小尺寸。
- 基于英特尔® 数学核心库的本机处理器优化实施,可提高大尺寸的速度。
- 本机 64 位支持。
- GPU计算
- GPU 计算:将计算卸载到 GPU。
- 数据尽可能长时间地保留在 GPU 上,以获得最佳性能。
- 向量
- 密集的向量。
- 带向量。
- 常数向量。
- 行、列和对角向量。
- 矢量视图。
- 向量运算
- 基本算术运算。
- 逐元素操作。
- 重载算术运算符。
- 范数,点积。
- 最大值和最小值。
- 向量函数(正弦、余弦等)
- 矩阵
- 一般矩阵。
- 三角矩阵。
- 实对称矩阵和复埃尔米特矩阵。
- 带状矩阵。
- 对角矩阵。
- 矩阵视图。
- 矩阵运算
- 基本算术运算。
- 矩阵向量积。
- 重载算术运算。
- 逐元素操作。
- 行和列缩放。
- 规范、等级、条件数。
- 奇异值、特征值和特征向量。
- 矩阵分解
- LU 分解。
- QR 分解。
- 乔列斯基分解。
- 奇异值分解。
- 对称特征值分解。
- 非对称特征值分解。
- 带状 LU 和 Cholesky 分解。
- 稀疏矩阵
- 稀疏向量。
- 稀疏矩阵。
- 压缩稀疏列格式的矩阵。
- 稀疏 LU 分解。
- 读取 Matrix Market 格式的矩阵。
- 线性方程和最小二乘法
- 用于矩阵和分解的共享 API。
- 行列式、逆元、数值等级、条件数。
- 求解具有 1 个或多个右侧的方程。
- 使用 QR 或奇异值分解的最小二乘解决方案。
- 摩尔-彭罗斯伪逆。
- 非负最小二乘法 (NNLS)。
统计库功能
- 描述性统计
- 集中趋势的度量:平均值、中位数、截尾平均值、调和平均值、几何平均值。
- 尺度测量:方差、标准差、极差、四分位距、平均值和中位数的绝对偏差。
- 高矩:偏度、峰度。
- 概率分布
- 概率密度函数 (PDF)。
- 累积分布函数(CDF)。
- 百分位数或逆累积分布函数。
- 矩:均值、方差、偏度和峰度。
- 从任何分布生成随机样本。
- 选定分布的参数估计。
- 连续概率分布
- 贝塔分布。
- 柯西分布。
- 卡方分布。
- Erlang 分布。
- 指数分布。
- F分布。
- 伽马分布。
- 广义帕累托分布。
- 甘贝尔分布。
- 拉普拉斯分布。
- 物流配送。
- 对数正态分布。
- 正态分布。
- 帕累托分布。
- 分段分布。
- 瑞利分布。
- 学生 t 分布。
- 转换后的 beta 分布。
- 变换后的伽玛分布。
- 三角形分布。
- 均匀分布。
- 威布尔分布。
- 离散概率分布
- 伯努利分布。
- 二项分布。
- 几何分布。
- 超几何分布。
- 负二项分布。
- 泊松分布。
- 均匀分布。
- 多元概率分布
- 多元正态分布。
- 狄利克雷分布。
- 直方图
- 一维直方图。
- 与直方图相关的概率分布。
- 一般线性模型
- 一般线性模型和广义线性模型计算的基础设施。
- 方差分析。
- 回归分析。
- 模型特定的假设检验。
- 方差分析 (ANOVA)
- 一向和双向方差分析。
- 具有重复测量的单向方差分析。
- 回归分析
- 简单回归、多元回归和多项式回归。
- 非线性回归。
- 逻辑回归。
- 广义线性模型。
- 灵活的回归模型。
- 方差-协方差矩阵、回归矩阵。
- 回归参数的置信区间和显着性检验。
- 时间序列分析
- 将多个观察变量视为一个单元。
- 更改时间序列的频率。
- 自动应用预定义的聚合器。
- 高级聚合器:成交量加权平均。
- 时间序列数据的转换
- 滞后时间序列、总和、乘积。
- 变化、变化百分比、增长率。
- 推断变化、变化百分比、增长率。
- 期间至今的总和与差异。
- 简单、指数、加权移动平均线。
- Savitsky-Golay 平滑。
- 多元模型
- 主成分分析(PCA)。
- 层次聚类。
- K-均值聚类。
- 统计检验
- 均值检验:一个样本 z 检验,一个样本 t 检验。
- 配对和不配对的双样本 t 检验,用于检测两个样本均值之间的差异。
- 两个样本的比率 z 检验。
- 一个样本卡方方差检验。
- 两个方差之比的 F 检验。
- 一和两个样本柯尔莫哥洛夫-斯米尔诺夫检验。
- 安德森-达林正态性检验。
- 卡方拟合优度检验。
- Bartlett 和 Levene 检验方差齐性。
- 麦克尼马尔和斯图尔特-麦克斯韦测试。
- 随机数生成
- 与.NET Framework 的System.Random 兼容。
- 四种发电机,具有不同的质量、周期和速度,以满足您的应用需求。
- 从任何分布生成随机样本。
- 福雷和霍尔顿序列。
- 洗牌器和随机计数器。
相关文章:

.NET8构建统计Extreme Optimization Numerical Libraries
为 .NET 8 构建统计应用程序 Extreme Optimization Numerical Libraries for .NET V8.1.22 添加了对 .NET 8 的支持,使您可以使用最新版本的 Microsoft 平台。 Extreme Optimization Numerical Libraries for .NET 是通用数学和统计类的集合,为技术和统计…...
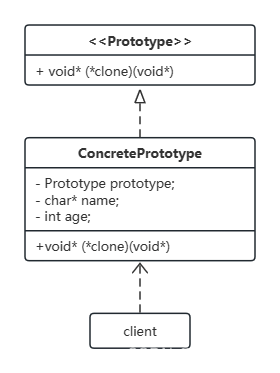
07-原型模式-C语言实现
原型模式: Specify the kinds of objects to create using a prototypical instance,and create new objects by copying this prototype.(用原型实例指定创建对象的种类, 并且通过拷贝这些原型创建新的对象。 ) UML图࿱…...

深度学习与深度迁移学习有什么区别?
深度学习包含深度迁移学习,它们都利用了深层神经网络(Deep Neural Network,DNN)来处理数据,并从中学习特征。但是,它们也有一些区别。 深度学习是一种机器学习方法,它通过多层神经网络来自动学…...
创建Asp.net MVC项目Ajax实现视图页面数据与后端Json传值显示
简述回顾 继上篇文章创建的mvc传值这里说明一下Json传值。在mvc框架中,不可避免地会遇到前台传值到后台,前台接收后台的值的情况(前台指view,后台指controller),有时只需要从控制器中返回一个处理的结果&a…...
)
1089 Insert or Merge (插入排序,相邻归并排序,附模拟实现)
注意点1:判断插入排序不能从头开始判断是否为目标数组, 比如:初始为1 2 3 4 3,目标数组也为1 2 3 4 3,则如果是从头开始推的,则下一步会变成1 2 3 4 3,而下一步应该是 1 2 3 3 4。所以我们应该…...

基于算能的国产AI边缘计算盒子8核心A53丨17.6Tops算力
边缘计算盒子 8核心A53丨17.6Tops算力 ● 可提供17.6TOPS(INT8)的峰值计算能力、2.2TFLOPS(FP32)的高精度算力,单芯片最高支持32路H.264 & H.265的实时解码能力。 ● 适配Caffe/TensorFlow/MxNet/PyTorch/ ONNX/…...

Eaxyx 让圆球跟随鼠标移动
如果出现2023,代表配置成功: 进入Eaxy官方网站,点击文档: 选择 函数->绘图函数->initgraph: 可以看见initgraph()函数有如下三个参数: 现在我们想生成一个1280*720大小的窗口: 我们需写如下代码: 但…...
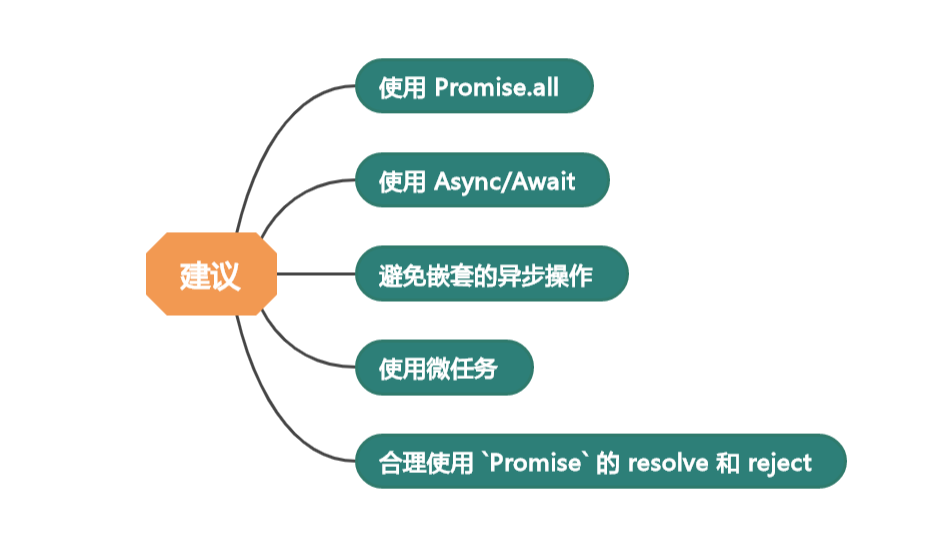
Node.js 事件循环:定时任务、延迟任务和 I/O 事件的艺术
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云…...

陪诊系统:基于自然语言处理的患者沟通创新
医疗领域的数字化转型正日益引入创新技术,其中基于自然语言处理(NLP)的陪诊系统成为提升患者沟通的一项关键技术。本文将深入研究这一领域,介绍陪诊系统如何借助NLP实现患者沟通的创新,并提供一个简单的Python代码示例…...

实用攻略——SD-WAN网络配置步骤详解
SD-WAN(软件定义广域网)作为一种新兴的网络技术,被广泛应用于构建高效、可靠的企业组网。 本文将详细介绍企业组网中SD-WAN涉及的配置过程,并提供一些配置技巧,以帮助企业快速了解企业组网的配置。通过使用SD-WAN技术&…...

无人机摄影测量
无人机摄影测量技术是传统航空摄影测量手段的有力补充,具有机动灵活、高效快速、精细准确、作业成本低、生产周期短、影像获取空间分辨率高、高危地区探测等优势。无人机与航空摄影测量相结合使得“无人机数字低空遥感”成为航空遥感领域的一个崭新发展方向。无人机…...
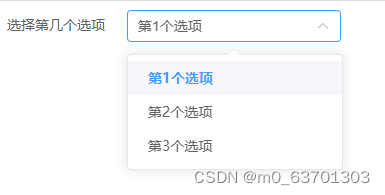
对el-select封装成组件使用
效果与直接使用el-select一样,多处用el-select显得代码冗余就进行了封装 效果图: el-select封装: <template><div class"my-select"><el-selectv-model"person.modelValue":placeholder"placehold…...

pytorch 多卡并行训练
目录 设置参数: 训练时参数: 调用命令: 设置参数: import argparseparser argparse.ArgumentParser()parser.add_argument(--batch_size, typeint, default64, helpBatch size for training)parser.add_argument(--local_rank…...

C# Bin、XML、Json的序列化和反序列化
1)序列化前的准备 声明类: [Serializable]public class BandItem{//JsonIgnore:当不想把某字段值序列化到Json时使用//[JsonIgnore]public string Name { get; set; }public string MusicStyle { get; set; }public string Masterpiece { ge…...

mediapipe+opencv实现保存图像中的人脸,抹去其他信息
mediapipeopencv MediaPipe本身不提供图像处理功能,它主要用于检测和跟踪人脸、手势、姿势等。如果您想要从图像中仅提取人脸主要信息并去除其他信息. # codingutf-8 """project: teatAuthor:念卿 刘file: test.pydate&…...

clickhouse的向量化执行
背景 clickhouse快的很大一部分原因来源于数据的向量化执行,本文就来看一下向量化执行和正常标量执行的区别 SIMD的向量化执行 从上图可知,clickhouse通过SIMD指令可以做到一个cpu周期操作两个向量的运算操作,比起普通的cpu指令效率提高了N…...

R语言实验三
1、读取一个文件并进行如下操作。 ①使用命令清空工作空间,使用read.table读取exam_1.txt文件,将文件保存到data变量中,数据第一行设置为列名,第一列是行名。 ②判断对象data是否为矩阵。 ③将对象转换为矩阵,记为d…...

springboot-mongodb-连接配置
文章目录 配置Maven依赖URL格式单节点配置示例副本集(含连接池配置) 配置Maven依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-mongodb</artifactId></dependenc…...

基于单片机的多功能视力保护器(论文+源码)
1.系统设计 多功能视力保护器在设计过程中能够对用户阅读过程中的各项数据信息进行控制,整体设计分为亮种模式,分别是自动模式,手动模式。在自动模式的控制下,当单片机检测当前光照不强且有人时就开启LED灯,并且会根据…...

如何保护 API 安全
为了收集有关 API 管理当前和未来状态的见解,我们邀请来自 18 家公司的 IT 专业人士分享他们的想法。我们问他们:“哪些技术和工具对于保护 API 最有效?” 他们告诉我们的是: 验证 我们经常向已知的 B2B 合作伙伴提供 API 访问权…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

如何在Windows本机安装Python并确保与Python.NET兼容
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用(Math::max) 2 函数接口…...
