【面试HOT200】二叉树——深度优先搜索篇
系列综述:
💞目的:本系列是个人整理为了秋招面试的,整理期间苛求每个知识点,平衡理解简易度与深入程度。
🥰来源:材料主要源于【CodeTopHot200】进行的,每个知识点的修正和深入主要参考各平台大佬的文章,其中也可能含有少量的个人实验自证,所有代码均优先参考最佳性能。
🤭结语:如果有帮到你的地方,就点个赞和关注一下呗,谢谢🎈🎄🌷!!!
🌈【C++】秋招&实习面经汇总篇
文章目录
- 基础知识
- 二叉树DFS基本算法
- 递归算法
- 非递归算法
- 相关题目
- 236. 二叉树的最近公共祖先
- 110. 判断平衡二叉树(后序遍历的示例)
- 222. 求树中结点的数量
- 226. 翻转二叉树
- 101. 对称二叉树
- 左叶子之和
- 二叉树的所有路径(带缓存的前序遍历)
- 符合总和的路径
- 参考博客
😊点此到文末惊喜↩︎
基础知识
二叉树DFS基本算法
递归算法
- 注意
- 左右子树不需要
if (root->left/rihgt),因为递归出口已经判断了 - 后序遍历有个好处:可以先收集和处理孩子,然后根节点再进行处理
// 前序遍历 void Traversal(TreeNode *root) {if (root == nullptr) return ;Doing(root->val); // 中Traversal(root->left); // 左Traversal(root->right); // 右 } // 中序遍历 void Traversal(TreeNode *root) {if (root == nullptr) return ;Traversal(root->left); // 左Doing(root->val); // 中Traversal(root->right); // 右 } // 后序遍历 void Traversal(TreeNode *root, vector<int> vec) {if (root == nullptr) return ;Traversal(root->left); // 左Traversal(root->right); // 右vec.emplace_back(root->val);// 中 } - 左右子树不需要
非递归算法
- 注意点
vector<int> preorderTraversal(TreeNode* root) {vector<int> res; // 结果容器stack<TreeNode*> st; // 深度栈if(root != nullptr) st.push(root); // 根非空则入栈// 遍历源容器while (!st.empty()) { // key:注意使用的全部结点都是node// 先记录TreeNode *node = st.top();st.pop();// 后操作if (node != nullptr) {// 压入允许为逆序,注意根节点要后压入nullptrif (node->right) st.push(node->right); if (node->left) st.push(node->left); st.push(node);st.push(nullptr);} else {// 先记录node = st.top();st.pop();// 后操作res.emplace_back(node->val);}}return res; }
相关题目
236. 二叉树的最近公共祖先
- 题目
- 给定一个二叉树, 找到该树中两个指定节点p和q的最近公共祖先。
- 复杂度分析:
- 时间复杂度 O(N): 其中 N为二叉树节点数;最差情况下,需要递归遍历树的所有节点。
- 空间复杂度 O(N): 最差情况下,递归深度达到 N
- 思路
- 递归出口:如果不是nullptr表示找到了
- 后序遍历:优先遍历左右子树并进行记录
- 结点处理
- 如果左右子树都非空,一定表示该结点为公共祖先结点
- 如果有一个为空,则向上传递非空的那个结点
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {// 递归出口:返回标志,不为空说明是祖先结点if (root == p || root == q || root == nullptr) return root;// 后序遍历TreeNode *left = lowestCommonAncestor(root->left, p, q);TreeNode *right = lowestCommonAncestor(root->right, p, q);// 中间结点的处理// 左右都非空表示,该节点为公共祖先结点 if (left != nullptr && right != nullptr)return root;// 有一个为空表示,if (left == nullptr) return right;if (right == nullptr) return left;return root;
}
110. 判断平衡二叉树(后序遍历的示例)
- 递归法
- 给定一个二叉树,判断它是否是高度平衡的二叉树。
- 一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。
// 初始化ans为true,最后看ans是否为false即可 int depth(TreeNode* root, bool &ans) {if(!root) return 0;// 后序遍历int left=1+depth(root->left, ans);int right=1+depth(root->right, ans);if(abs(left-right) > 1) ans = false;// 对根结点的处理// 递归出口return max(left,right); // 返回树的高度 } // 尾递归优化:效率高 bool isBalanced(TreeNode* root) {if (root == nulllptr) return true;return abs(depth(root->left) - depth(root->right)) <= 1 && isBalanced(root->left) && isBalanced(root->right); }
222. 求树中结点的数量
- 题目
- 给你一棵 完全二叉树 的根节点 root ,求出该树的节点个数。
- 算法
int getNodesNum(TreeNode* cur) {if (cur == NULL) return 0;int leftNum = getNodesNum(cur->left); // 左int rightNum = getNodesNum(cur->right); // 右int treeNum = leftNum + rightNum + 1; // 中return treeNum; }
226. 翻转二叉树
- 给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。

TreeNode* invertTree(TreeNode* root) {auto self = [&](auto &&self, TreeNode *root){if (root == nullptr) return ;self(self, root->left);self(self, root->right);swap(root->left, root->right);return ;};self(self, root);return root;
}
101. 对称二叉树
- 题目
- 求一颗二叉树是否镜像对称

- 求一颗二叉树是否镜像对称
- 思路
- 根节点必定对称,关键是左右两子树的对称
- 左右两个孩子存在的情况下,递归比较左右两颗子树的情况
bool isSymmetric(TreeNode* root) {auto self = [&](auto && self, TreeNode *left, TreeNode *right)->bool{// 递归出口if (left == nullptr && right == nullptr) return true;else if (left != nullptr && right == nullptr) return false;else if (left == nullptr && right != nullptr) return false;else if (left->val != right->val) return false;// 后序遍历:递归比较并汇总结果bool outside = self(self, left->left, right->right);bool inside = self(self,left->right, right->left);bool is_same = outside && inside;// 返回结果return is_same;};return self(self, root->left, root->right);
}
左叶子之和
- 求二叉树的左叶子之和
- 遍历所有节点,对所求的特殊节点进行约束求值
if (node->left != nullptr && node->left->left == nullptr && node->left->right == nullptr)res += node->left->val;
二叉树的所有路径(带缓存的前序遍历)
- 递归
- 数字转化成字符串
to_string(number) - 字符串后追加子串
str.append(subStr) - 字符串删除某个位置之后的字符
str.erase(position)
// 数字型 void dfs(TreeNode*root,vector<int>path, vector<vector<int>> &res) {if(!root) return; //根节点为空直接返回// 中path.push_back(root->val); //作出选择if(!root->left && !root->right) //如果到叶节点 {res.push_back(path);return;}// 左dfs(root->left,path,res); //继续递归// 右dfs(root->right,path,res); } // 字符型 void binaryTree(TreeNode* root,string path,vector<string>&res) {if(root==NULL) return ;path.append(to_string(root->val));path.append("->");if(root->left==NULL&&root->right==NULL{path.erase(path.length()-2);res.push_back(path);}binaryTree(root->left,path,res);binaryTree(root->right,path,res); } vector<string> binaryTreePaths(TreeNode* root) {string path;vector<string>res;binaryTree(root,path,res);return res; } - 数字转化成字符串
符合总和的路径
- 题目
- 判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true;否则,返回 false
// 递归方式:前序遍历,并记录每条路径的和 bool hasPathSum(TreeNode* root, int targetSum) {bool flag = false;auto self = [&](auto &&self, TreeNode *root, int sum){// sum不可全局if (root == nullptr) return ;// 根结点的处理sum += root->val;cout << sum << ' ';if (root->left == nullptr && root->right == nullptr && targetSum == sum) flag = true;self(self, root->left, sum);self(self, root->right, sum);};self(self, root, 0);return flag; } // 非递归 bool hasPathSum(TreeNode* root, int targetSum) {// 初始化stack<TreeNode*> st;if(root != nullptr) st.push(root);int sum = 0;// 迭代while(!st.empty()){TreeNode *cur = st.top();if(cur != nullptr){st.pop();st.push(cur);st.push(nullptr);sum += cur->val;if(cur->right) st.push(cur->right);if(cur->left) st.push(cur->left);}else{st.pop();cur = st.top();st.pop();// 节点判断if(sum == targetSum&& cur->left == nullptr && cur->right == nullptr){return true;}else{// 回溯sum -= cur->val;}}}return false; }
🚩点此跳转到首行↩︎
参考博客
- 「代码随想录」47. 全排列 II:【彻底理解排列中的去重问题】详解
- codetop
- 力扣(LeetCode)Krahets
相关文章:

【面试HOT200】二叉树——深度优先搜索篇
系列综述: 💞目的:本系列是个人整理为了秋招面试的,整理期间苛求每个知识点,平衡理解简易度与深入程度。 🥰来源:材料主要源于【CodeTopHot200】进行的,每个知识点的修正和深入主要参…...

价值投资选股的方法
价值投资法是一种长期投资策略,其核心思想是寻找被市场低估的股票,即股票的市场价格低于其内在价值。这种策略认为,投资者应该关注公司的基本面,如盈利能力、成长潜力、财务状况等,而不是短期的市场波动。以下是价值投…...

java中如何将mysql里面的数据取出来然后通过stream流的方式进行数据处理代码实例?
在 Java 中使用 Stream 流的方式从 MySQL 数据库中取出数据并进行处理,你可以通过 JDBC(Java Database Connectivity)来实现。下面是一个简单的代码示例: import java.sql.*; import java.util.stream.Stream; public class MySQ…...

C++服务器 支持http、tcp protobuf、websocket,linux开源框架 零依赖轻松编译部署 Reactor
开源地址: https://github.com/crust-hub/tubekit/tree/main Github:https://github.com/gaowanlu 诚招有兴趣的小伙伴加入开发维护 Tubekit The C TCP server framework based on the Reactor model continues to implement POSIX thread pool, Epoll, non blocking IO, obj…...

1688API接口系列,1688开放平台接口使用方案(商品详情数据+搜索商品列表+商家订单类)
1688商品详情接口是指1688平台提供的API接口,用于获取商品详情信息。通过该接口,您可以获取到商品的详细信息,包括商品标题、价格、库存、描述、图片等。 要使用1688商品详情接口,您需要先申请1688的API权限,并获取ac…...
CentOS服务器网页版Rstudio-server及R包批量安装最佳实践
CentOS服务器安装网页版Rstudio-server及R包批量安装 以下为CentOS 7/8的Rstudio-server安装、配置和R包安装操作 1. 软件包安装 Centos 7安装 # 下载安装包,大小115.14 MB wget -c https://download2.rstudio.org/server/centos7/x86_64/rstudio-server-rhel-…...

centos7内核升级(k8s基础篇)
1.查看系统内核版本信息 uname -r 2.升级内核 2.1更新yum源仓库 yum -y update更新完成后,启用 ELRepo 仓库并安装ELRepo仓库的yum源 ELRepo 仓库是基于社区的用于企业级 Linux 仓库,提供对 RedHat Enterprise (RHEL) 和 其他基于 RHEL的 Linux 发行…...

数据结构与算法设计分析——NP完全理论
目录 一、P类问题与NP类问题的定义二、常见的NP类问题(一)旅行商问题(TSP)(二)哈密尔顿回路问题(三)判断回路问题(四)图的着色问题(五)…...
AGNES层次聚类
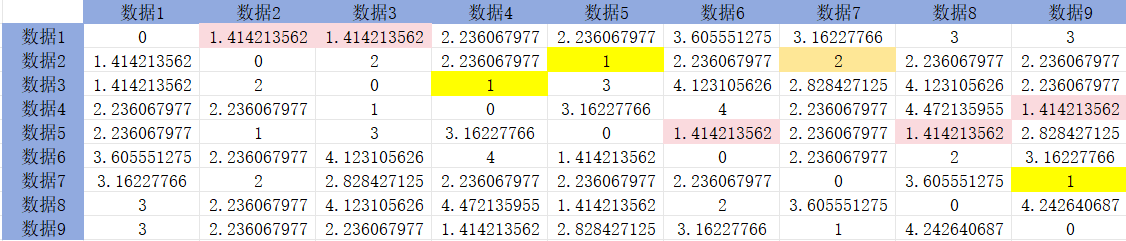
已知数据集D中有9个数据点,分别是(1,2),(2,3),(2,1), (3,1),(2,4),(3,5),(4,3),(1,5),(4,2)。要求: (1)采用层次聚类的聚集算法进行聚类,k2。 (2)距离计算采用欧几里得距离。 (3)簇之间的距离采用单链接方…...
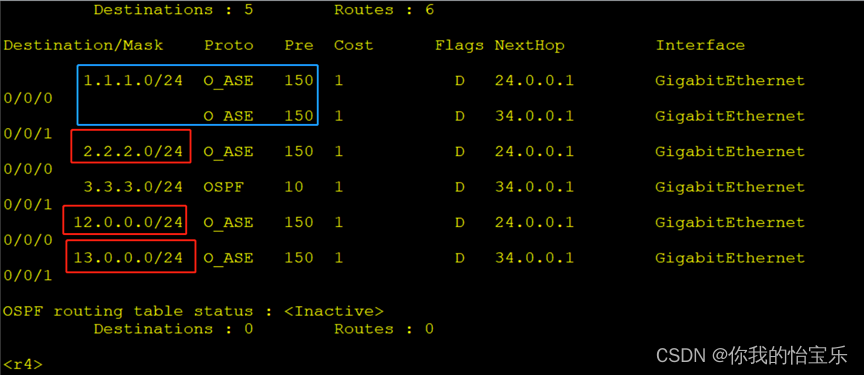
HCIP —— 双点重发布 + 路由策略 实验
目录 实验拓扑: 实验要求: 实验配置: 1.配置IP地址 2.配置动态路由协议 —— RIP 、 OSPF R1 RIP R4 OSPF R2 配置RIP、OSPF 双向重发布 R3配置RIP、OSPF 双向重发布 3.查询路由表学习情况 4.使用路由策略控制选路 R2 R3 5.检…...

Python标准库:datetime模块【侯小啾python领航班系列(二十五)】
Python标准库:datetime模块【侯小啾python领航班系列(二十五)】 大家好,我是博主侯小啾, 🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ🌹꧔ꦿ…...
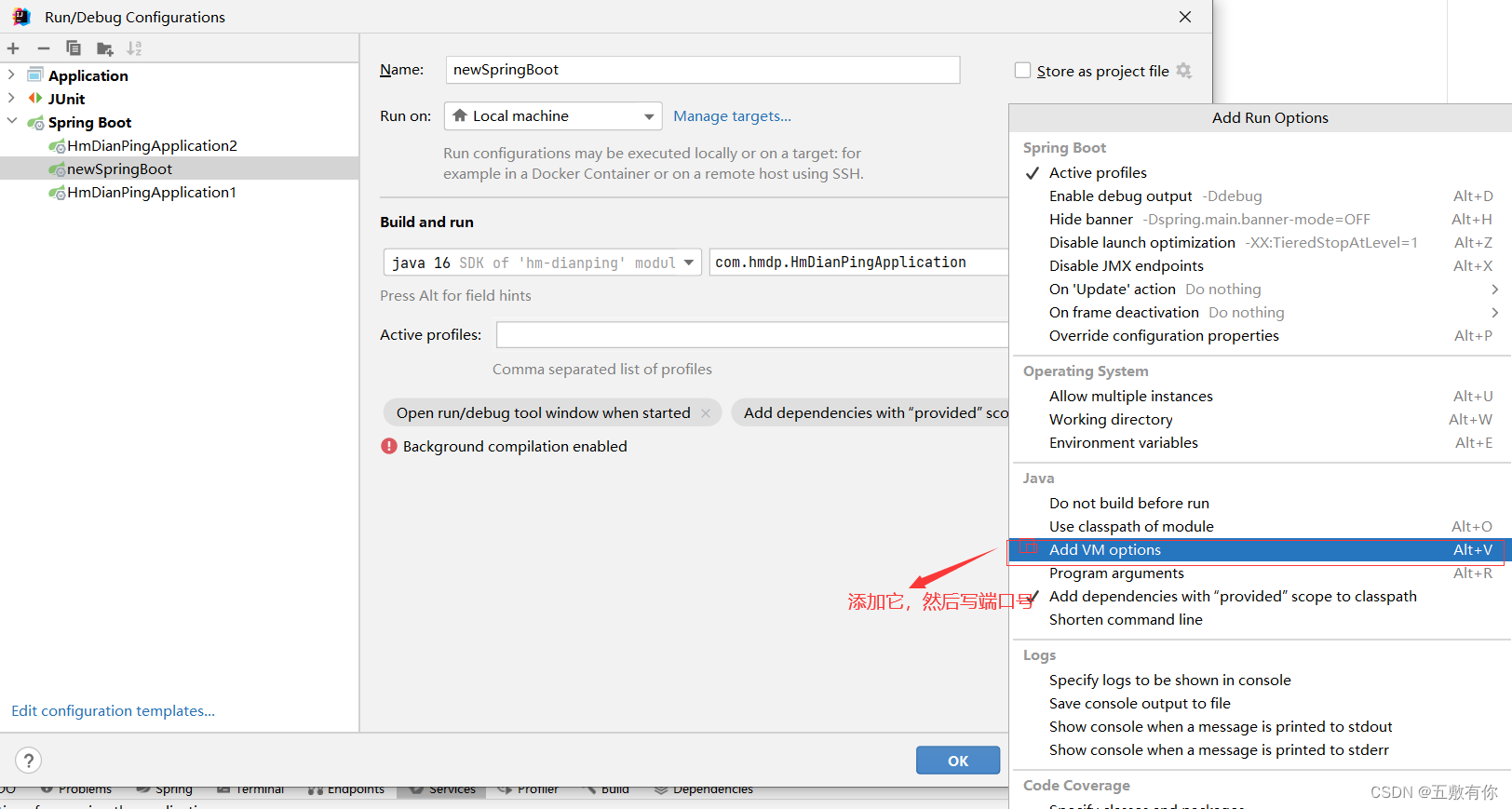
新版idea如何开启多台JVM虚拟机
1.看看自己的项目 2.可能开始的时候啥也没有,就点Run Configuration Type 3.再点击Edit Configurations... 4.点击号添加SpringBoot 5.主类选择一下,一般就一个,点他选了就行。 6.然后点击Modify Options 选择添加add VM Options 7.点击appl…...

软件工程单选多选补充
2. 4. 5. 6. 7. 8. 9. 10. 12。 13....
6-66.时间
本题要求输入小时、分钟和秒数,并将其输出。针对时间表示中出现的异常进行处理。例如小时数不应超过23,分钟不应超过59,秒数不应超过59。此外,以上三个变量均应大于等于0。 输入样例: 在这里给出三组输入。例如&…...
面试多线程八股文十问十答第一期
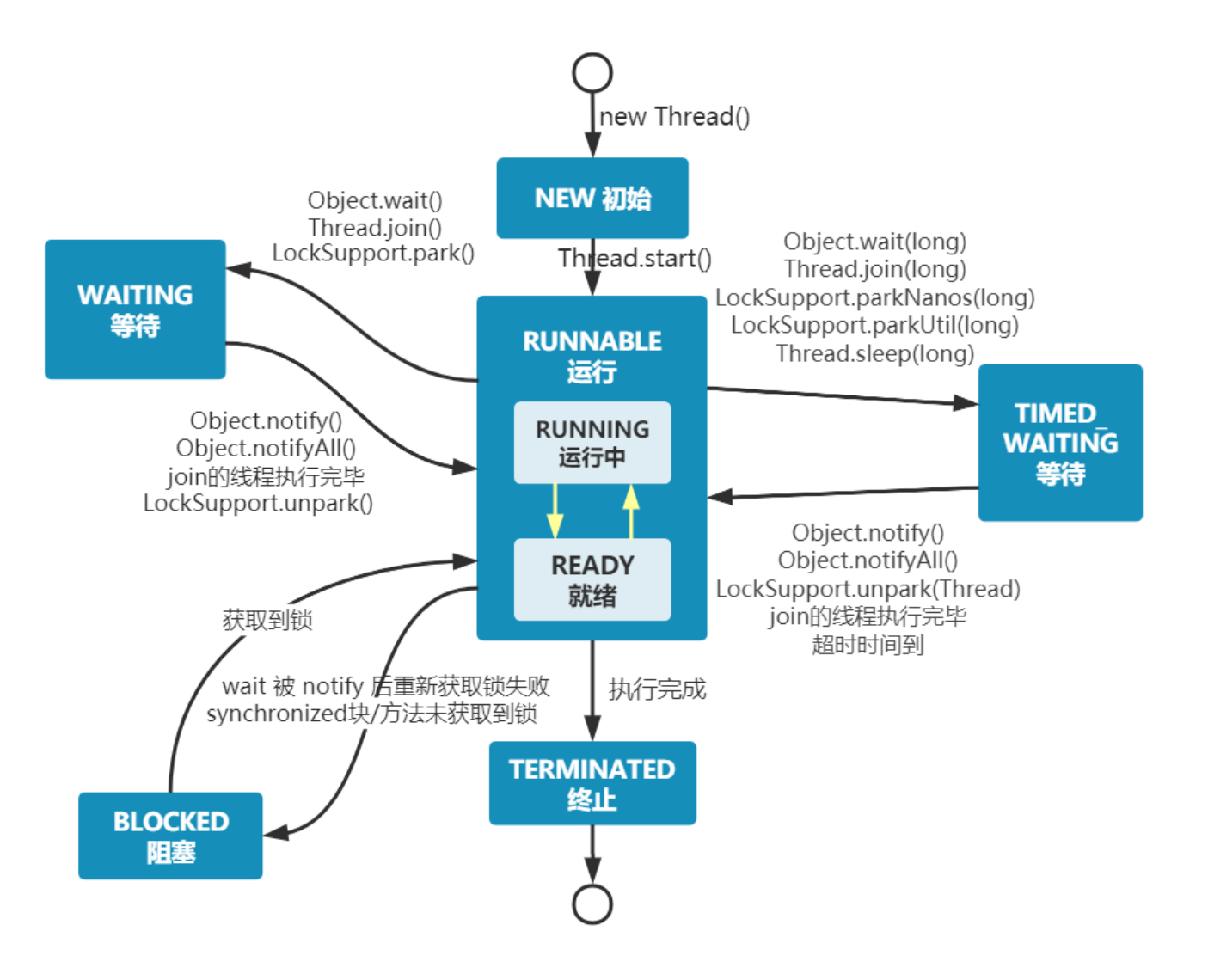
面试多线程八股文十问十答第一期 作者:程序员小白条,个人博客 相信看了本文后,对你的面试是有一定帮助的! ⭐点赞⭐收藏⭐不迷路!⭐ 1.ThreadLocal如何实现线程安全 Java的ThreadLocal是一个线程本地变量࿰…...
Mybatis 操作续集(结合上文)
当我们增加一个数据之后,如果我们想要获取它的 Id 进行别的操作,我们该如何获取 Id 呢? 用那个Options package com.example.mybatisdemo.mapper;import com.example.mybatisdemo.model.UserInfo; import org.apache.ibatis.annotations.*;import java.util.List;Mapper pub…...
JVM基础篇:垃圾回收
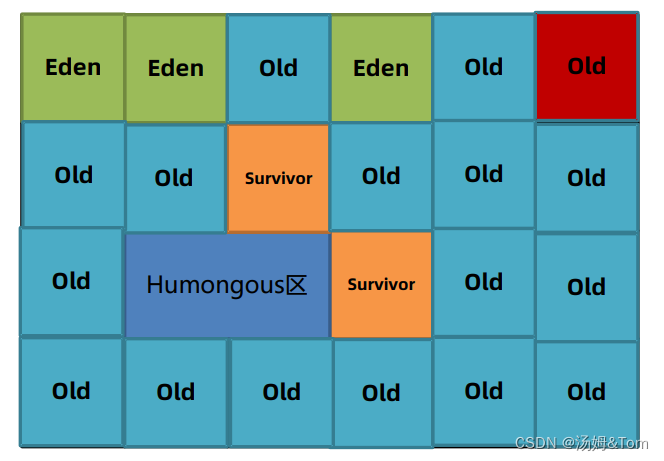
目录 1.前言 1.1C/C的内存管理 1.2Java的内存管理 2.方法区的回收 3.堆回收 3.1引用计数法和可达性分析法 3.2五种对象引用 强引用 软引用 弱引用 虚引用 终结器引用 3.3垃圾回收算法评价标准 ①吞吐量 ②最大暂停时间 ③堆使用效率 3.4垃圾回收算法 ①标记清…...

蓝桥杯ACwing习题
题目 :https://www.acwing.com/problem/content/4409/ 解析 :根据题目我们可以知道 问的是方案数 那么首先就想到了 dp 仔细想一下 发现类似于蒙德里安的梦想那道状态压缩的题 , 所以我们先考虑怎么定义 f[i][j] f[i][j] 表示的是 已经放了…...
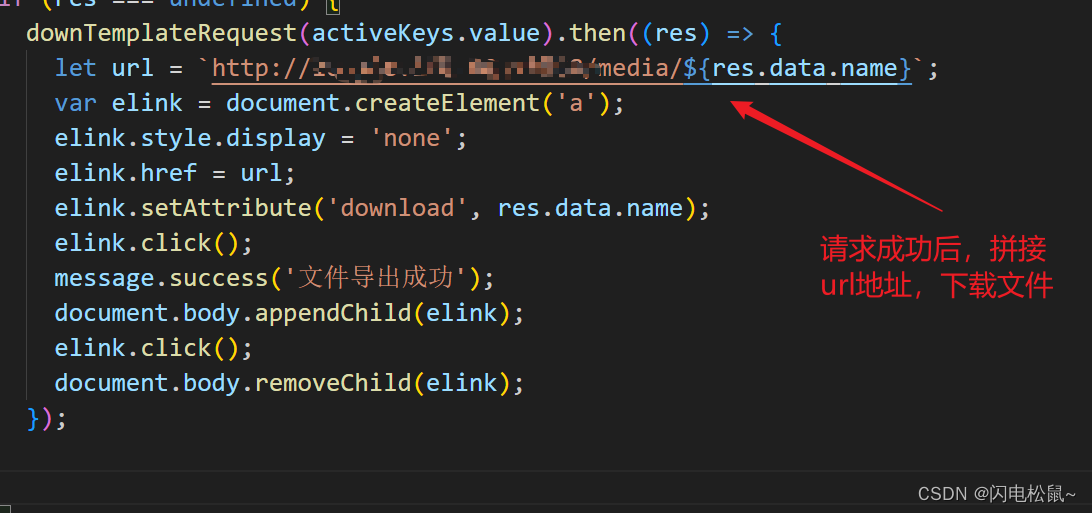
vue发送请求携带token,拼接url地址下载文件
封装请求 ,该请求为普通的get请求 该请求返回值为: 请求成功之后拼接URL地址下载文件 代码块 downTemplateRequest(activeKeys.value).then((res) > {let url http://47.169.168.99:18888/media/${res.data.name};var elink document.createElemen…...

【PTA-C语言】编程练习3 - 循环结构Ⅱ
如果代码存在问题,麻烦大家指正 ~ ~有帮助麻烦点个赞 ~ ~ 编程练习3 - 循环结构(9~15) 7-9 特殊a串数列求和(分数 15)7-10 穷举法搬运砖块问题(分数 15)7-11 数字金字塔(分数 15&…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...
