有序表常见题型
给定一个数组arr和两个整数a和b求arr中有多少个子数组累加和在a到b这个范围上返回达标的子数组数量
如【3,6,1,9,2】达标的子数组通过暴力求解的方式时间复杂度为O(N的三次方)【找每个子数组占用O(N的二次方)的时间复杂度,然后再算每个子数组的和占用O(N)的时间复杂度总的占用了O(N的三次方的时间复杂度)】
用前缀和的思想可以将时间复杂度降低到O(N的二次方的时间复杂度)
这个题有一个O(N*logN的解法)
分析:假设现在来到i位置,子数组必须以i位置的数结尾达标的有多少个,依次计算,最后求和则得到最终的结果。
假设要求必须以17结尾的子数组范围在[10,60]的有多少个,
假设现在0-17的前缀和是100,假设0-5的前缀和是5,那么可以推出6-17的累加和为95。
那么只要能够找到任何一个前缀和落在[40,90]的范围,那么就能得到以17结尾的子数组落在[10,60]范围。
做法:
有如下数组:
[3,-2,4,3,6,-1] 范围是[1,5]的,假设有一个结构,这个结构是接收前缀和的,那么对于遍历到的当前数x,则需要判断当前数x是否在[1,5]的范围上,以及它的前缀和是否存在落在[sum(x)-5,sum(x)-1]范围上。
那么对于如上数组:
第一步:首先是一个数也没有的时候,我的前缀和结构提前放入一个0,我要整体以0位置结尾落在1-5的范围上,我就在结构中查有多少个前缀和落在[-2,2]上,发现有一个,然后我再将自己的前缀和3扔进前缀和结构
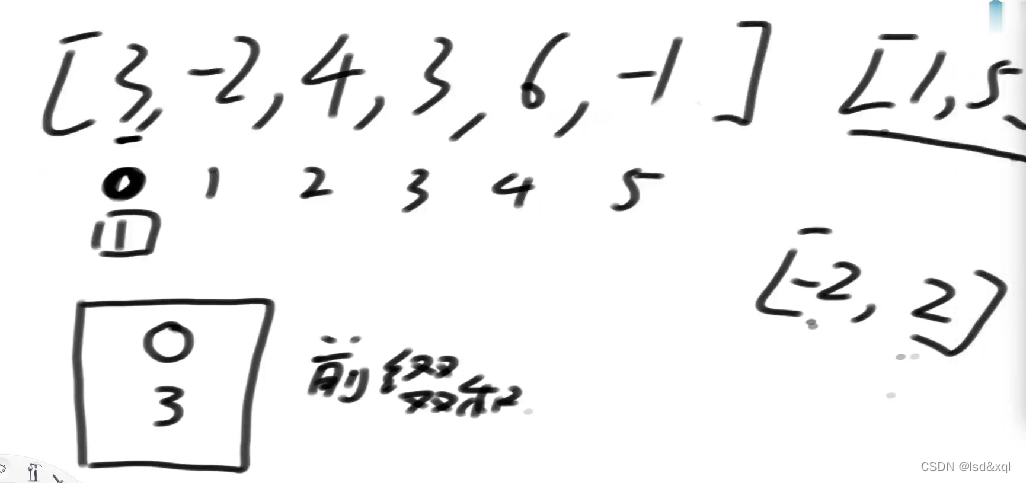
第二步:来到1位置,整体前缀和是1,那么则需要找到在这个前缀和结构中范围落在[-4,0]上面,发现有1个,然后我再将1位置的前缀和加入
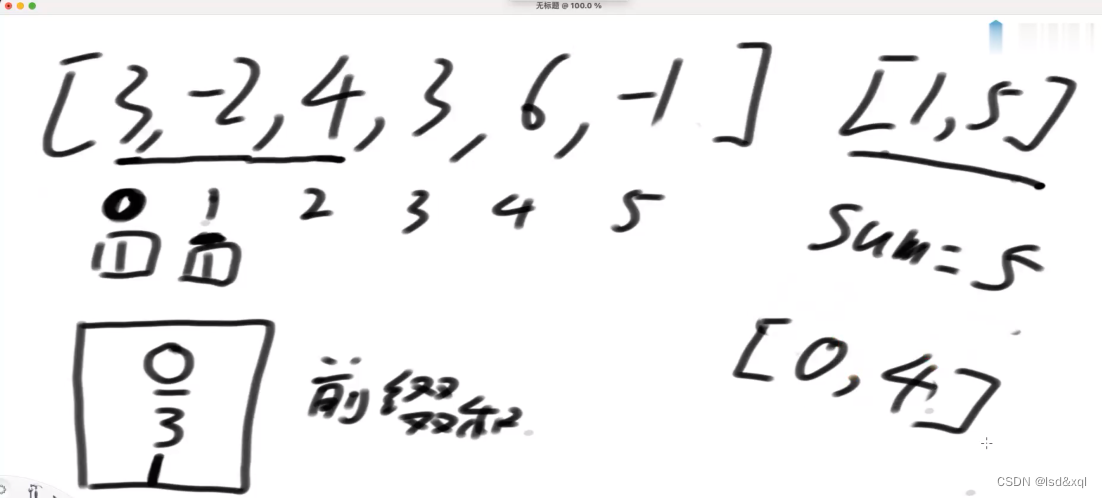
第三步:来到2位置,前缀和为5,那么需要找到有多少前缀和范围落在[0,4]范围上,发现有三个,再将5加入结构中。
依次类推下去得到最终的结果。
如何实现这个前缀和结构:
结构的特点:
1、这个结构能往里加整数
2、能够接收一个数字范围并且能够返回满足数字范围上的数有多少个
3、这个结构能接收重复的数字(我多个范围可能有相同的前缀和)
那么我可以做一个小于某个key值的接口把范围内的数给拼接出来。
问题:
有序表是不能有重复数字,解决方案:
我们可以将重复数字压在一起从而实现解决。
public class CountofRangeSum {public static int countRangeSum1(int[] nums, int lower, int upper) {int n = nums.length;long[] sums = new long[n + 1];for (int i = 0; i < n; ++i)sums[i + 1] = sums[i] + nums[i];return countWhileMergeSort(sums, 0, n + 1, lower, upper);}private static int countWhileMergeSort(long[] sums, int start, int end, int lower, int upper) {if (end - start <= 1)return 0;int mid = (start + end) / 2;int count = countWhileMergeSort(sums, start, mid, lower, upper)+ countWhileMergeSort(sums, mid, end, lower, upper);int j = mid, k = mid, t = mid;long[] cache = new long[end - start];for (int i = start, r = 0; i < mid; ++i, ++r) {while (k < end && sums[k] - sums[i] < lower)k++;while (j < end && sums[j] - sums[i] <= upper)j++;while (t < end && sums[t] < sums[i])cache[r++] = sums[t++];cache[r] = sums[i];count += j - k;}System.arraycopy(cache, 0, sums, start, t - start);return count;}public static class SBTNode {//参与排序的keypublic long key;//左孩子右孩子public SBTNode l;public SBTNode r;//平衡因子public long size; // 不同key的size//附加的数据项public long all; // 总的sizepublic SBTNode(long k) {key = k;size = 1;all = 1;}}public static class SizeBalancedTreeSet {private SBTNode root;private HashSet<Long> set = new HashSet<>();private SBTNode rightRotate(SBTNode cur) {long same = cur.all - (cur.l != null ? cur.l.all : 0) - (cur.r != null ? cur.r.all : 0);SBTNode leftNode = cur.l;cur.l = leftNode.r;leftNode.r = cur;leftNode.size = cur.size;cur.size = (cur.l != null ? cur.l.size : 0) + (cur.r != null ? cur.r.size : 0) + 1;// all modifyleftNode.all = cur.all;cur.all = (cur.l != null ? cur.l.all : 0) + (cur.r != null ? cur.r.all : 0) + same;return leftNode;}private SBTNode leftRotate(SBTNode cur) {long same = cur.all - (cur.l != null ? cur.l.all : 0) - (cur.r != null ? cur.r.all : 0);SBTNode rightNode = cur.r;cur.r = rightNode.l;rightNode.l = cur;rightNode.size = cur.size;cur.size = (cur.l != null ? cur.l.size : 0) + (cur.r != null ? cur.r.size : 0) + 1;// all modifyrightNode.all = cur.all;cur.all = (cur.l != null ? cur.l.all : 0) + (cur.r != null ? cur.r.all : 0) + same;return rightNode;}private SBTNode maintain(SBTNode cur) {if (cur == null) {return null;}long leftSize = cur.l != null ? cur.l.size : 0;long leftLeftSize = cur.l != null && cur.l.l != null ? cur.l.l.size : 0;long leftRightSize = cur.l != null && cur.l.r != null ? cur.l.r.size : 0;long rightSize = cur.r != null ? cur.r.size : 0;long rightLeftSize = cur.r != null && cur.r.l != null ? cur.r.l.size : 0;long rightRightSize = cur.r != null && cur.r.r != null ? cur.r.r.size : 0;if (leftLeftSize > rightSize) {cur = rightRotate(cur);cur.r = maintain(cur.r);cur = maintain(cur);} else if (leftRightSize > rightSize) {cur.l = leftRotate(cur.l);cur = rightRotate(cur);cur.l = maintain(cur.l);cur.r = maintain(cur.r);cur = maintain(cur);} else if (rightRightSize > leftSize) {cur = leftRotate(cur);cur.l = maintain(cur.l);cur = maintain(cur);} else if (rightLeftSize > leftSize) {cur.r = rightRotate(cur.r);cur = leftRotate(cur);cur.l = maintain(cur.l);cur.r = maintain(cur.r);cur = maintain(cur);}return cur;}private SBTNode add(SBTNode cur, long key, boolean contains) {if (cur == null) {return new SBTNode(key);} else {cur.all++;if (key == cur.key) {return cur;} else { // 还在左滑或者右滑if (!contains) {cur.size++;}if (key < cur.key) {cur.l = add(cur.l, key, contains);} else {cur.r = add(cur.r, key, contains);}return maintain(cur);}}}public void add(long sum) {boolean contains = set.contains(sum);root = add(root, sum, contains);set.add(sum);}public long lessKeySize(long key) {SBTNode cur = root;long ans = 0;while (cur != null) {if (key == cur.key) {//左树不为空则加上左树的allreturn ans + (cur.l != null ? cur.l.all : 0);} else if (key < cur.key) {cur = cur.l;} else {ans += cur.all - (cur.r != null ? cur.r.all : 0);cur = cur.r;}}return ans;}// > 7 8...// <8 ...<=7public long moreKeySize(long key) {return root != null ? (root.all - lessKeySize(key + 1)) : 0;}}public static int countRangeSum2(int[] nums, int lower, int upper) {// 黑盒,加入数字(前缀和),不去重,可以接受重复数字//支持查询 < num , 有几个数?SizeBalancedTreeSet treeSet = new SizeBalancedTreeSet();long sum = 0;int ans = 0;treeSet.add(0);// 一个数都没有的时候,就已经有一个前缀和累加和为0,for (int i = 0; i < nums.length; i++) {sum += nums[i];//之前有多少个前缀和落在[sum - upper, sum - lower]// [10, 20] ? 如果要查落在10到20范围上的数有多少个// 那么需要查< 10 的有多少个 < 21 的有多少个long a = treeSet.lessKeySize(sum - lower + 1);long b = treeSet.lessKeySize(sum - upper);//加上结果ans += a - b;//放入当前前缀和treeSet.add(sum);}return ans;}// for testpublic static void printArray(int[] arr) {for (int i = 0; i < arr.length; i++) {System.out.print(arr[i] + " ");}System.out.println();}// for testpublic static int[] generateArray(int len, int varible) {int[] arr = new int[len];for (int i = 0; i < arr.length; i++) {arr[i] = (int) (Math.random() * varible);}return arr;}public static void main(String[] args) {int len = 200;int varible = 50;for (int i = 0; i < 10000; i++) {int[] test = generateArray(len, varible);int lower = (int) (Math.random() * varible) - (int) (Math.random() * varible);int upper = lower + (int) (Math.random() * varible);int ans1 = countRangeSum1(test, lower, upper);int ans2 = countRangeSum2(test, lower, upper);if (ans1 != ans2) {printArray(test);System.out.println(lower);System.out.println(upper);System.out.println(ans1);System.out.println(ans2);}}}}
有一个滑动窗口:
1)L是滑动窗口最左位置,R是滑动窗口最右位置,一开始LR都在数组左侧
2)任何一步都可能R往右移动表示某个数进了窗口
3)任何一步都可能L往右动,表示某个数出了窗口
想知道每一个窗口状态的中位数
还是想象有这样一个结构:
1)这个结构可以接收数字,也可以支持一个一个删除数也可以都删除
2)如果n等于奇数则取中间的数,如果为偶数则取中间两个数除以2
3)可以加入重复数字
public class SlidingWindowMedian {public static class SBTNode<K extends Comparable<K>> {public K key;public SBTNode<K> l;public SBTNode<K> r;public int size;public SBTNode(K k) {key = k;size = 1;}}public static class SizeBalancedTreeMap<K extends Comparable<K>> {private SBTNode<K> root;private SBTNode<K> rightRotate(SBTNode<K> cur) {SBTNode<K> leftNode = cur.l;cur.l = leftNode.r;leftNode.r = cur;leftNode.size = cur.size;cur.size = (cur.l != null ? cur.l.size : 0) + (cur.r != null ? cur.r.size : 0) + 1;return leftNode;}private SBTNode<K> leftRotate(SBTNode<K> cur) {SBTNode<K> rightNode = cur.r;cur.r = rightNode.l;rightNode.l = cur;rightNode.size = cur.size;cur.size = (cur.l != null ? cur.l.size : 0) + (cur.r != null ? cur.r.size : 0) + 1;return rightNode;}private SBTNode<K> maintain(SBTNode<K> cur) {if (cur == null) {return null;}int leftSize = cur.l != null ? cur.l.size : 0;int leftLeftSize = cur.l != null && cur.l.l != null ? cur.l.l.size : 0;int leftRightSize = cur.l != null && cur.l.r != null ? cur.l.r.size : 0;int rightSize = cur.r != null ? cur.r.size : 0;int rightLeftSize = cur.r != null && cur.r.l != null ? cur.r.l.size : 0;int rightRightSize = cur.r != null && cur.r.r != null ? cur.r.r.size : 0;if (leftLeftSize > rightSize) {cur = rightRotate(cur);cur.r = maintain(cur.r);cur = maintain(cur);} else if (leftRightSize > rightSize) {cur.l = leftRotate(cur.l);cur = rightRotate(cur);cur.l = maintain(cur.l);cur.r = maintain(cur.r);cur = maintain(cur);} else if (rightRightSize > leftSize) {cur = leftRotate(cur);cur.l = maintain(cur.l);cur = maintain(cur);} else if (rightLeftSize > leftSize) {cur.r = rightRotate(cur.r);cur = leftRotate(cur);cur.l = maintain(cur.l);cur.r = maintain(cur.r);cur = maintain(cur);}return cur;}private SBTNode<K> findLastIndex(K key) {SBTNode<K> pre = root;SBTNode<K> cur = root;while (cur != null) {pre = cur;if (key.compareTo(cur.key) == 0) {break;} else if (key.compareTo(cur.key) < 0) {cur = cur.l;} else {cur = cur.r;}}return pre;}private SBTNode<K> add(SBTNode<K> cur, K key) {if (cur == null) {return new SBTNode<K>(key);} else {cur.size++;if (key.compareTo(cur.key) < 0) {cur.l = add(cur.l, key);} else {cur.r = add(cur.r, key);}return maintain(cur);}}private SBTNode<K> delete(SBTNode<K> cur, K key) {cur.size--;if (key.compareTo(cur.key) > 0) {cur.r = delete(cur.r, key);} else if (key.compareTo(cur.key) < 0) {cur.l = delete(cur.l, key);} else {if (cur.l == null && cur.r == null) {// free cur memory -> C++cur = null;} else if (cur.l == null && cur.r != null) {// free cur memory -> C++cur = cur.r;} else if (cur.l != null && cur.r == null) {// free cur memory -> C++cur = cur.l;} else {SBTNode<K> pre = null;SBTNode<K> des = cur.r;des.size--;while (des.l != null) {pre = des;des = des.l;des.size--;}if (pre != null) {pre.l = des.r;des.r = cur.r;}des.l = cur.l;des.size = des.l.size + (des.r == null ? 0 : des.r.size) + 1;// free cur memory -> C++cur = des;}}return cur;}private SBTNode<K> getIndex(SBTNode<K> cur, int kth) {if (kth == (cur.l != null ? cur.l.size : 0) + 1) {return cur;} else if (kth <= (cur.l != null ? cur.l.size : 0)) {return getIndex(cur.l, kth);} else {return getIndex(cur.r, kth - (cur.l != null ? cur.l.size : 0) - 1);}}public int size() {return root == null ? 0 : root.size;}public boolean containsKey(K key) {if (key == null) {throw new RuntimeException("invalid parameter.");}SBTNode<K> lastNode = findLastIndex(key);return lastNode != null && key.compareTo(lastNode.key) == 0 ? true : false;}public void add(K key) {if (key == null) {throw new RuntimeException("invalid parameter.");}SBTNode<K> lastNode = findLastIndex(key);if (lastNode == null || key.compareTo(lastNode.key) != 0) {root = add(root, key);}}public void remove(K key) {if (key == null) {throw new RuntimeException("invalid parameter.");}if (containsKey(key)) {root = delete(root, key);}}public K getIndexKey(int index) {if (index < 0 || index >= this.size()) {throw new RuntimeException("invalid parameter.");}return getIndex(root, index + 1).key;}}public static class Node implements Comparable<Node> {public int index;public int value;public Node(int i, int v) {index = i;value = v;}@Overridepublic int compareTo(Node o) {return value != o.value ? Integer.valueOf(value).compareTo(o.value): Integer.valueOf(index).compareTo(o.index);}}public static double[] medianSlidingWindow(int[] nums, int k) {SizeBalancedTreeMap<Node> map = new SizeBalancedTreeMap<>();for (int i = 0; i < k - 1; i++) {map.add(new Node(i, nums[i]));}double[] ans = new double[nums.length - k + 1];int index = 0;for (int i = k - 1; i < nums.length; i++) {map.add(new Node(i, nums[i]));if (map.size() % 2 == 0) {Node upmid = map.getIndexKey(map.size() / 2 - 1);Node downmid = map.getIndexKey(map.size() / 2);ans[index++] = ((double) upmid.value + (double) downmid.value) / 2;} else {Node mid = map.getIndexKey(map.size() / 2);ans[index++] = (double) mid.value;}map.remove(new Node(i - k + 1, nums[i - k + 1]));}return ans;}}
高效实现ArrayList的add(index,num),get(index),remove(index)方法要求时间复杂度为LogN
假设维持一棵树A左边出现的点的自然时序都比它早,然后A的右树自然时序都比A晚,S的自然时序都比B早,k的自然时序都比B晚
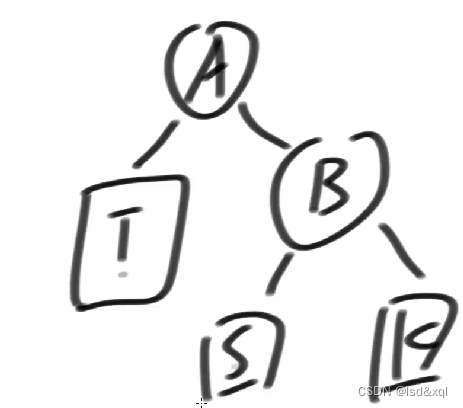
假设现在我们要左旋:
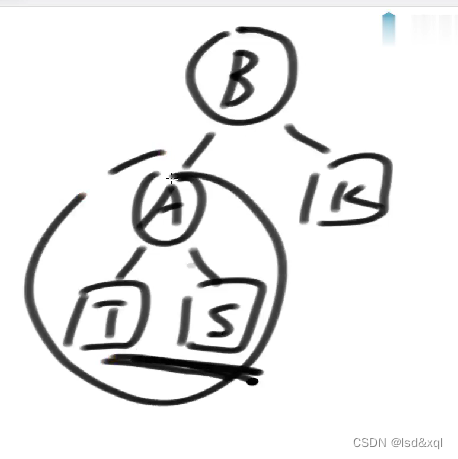
我的自然时序依然不变。
public class AddRemoveGetIndexGreat {public static class SBTNode<V> {public V value;public SBTNode<V> l;public SBTNode<V> r;public int size;public SBTNode(V v) {value = v;size = 1;}}public static class SbtList<V> {private SBTNode<V> root;private SBTNode<V> rightRotate(SBTNode<V> cur) {SBTNode<V> leftNode = cur.l;cur.l = leftNode.r;leftNode.r = cur;leftNode.size = cur.size;cur.size = (cur.l != null ? cur.l.size : 0) + (cur.r != null ? cur.r.size : 0) + 1;return leftNode;}private SBTNode<V> leftRotate(SBTNode<V> cur) {SBTNode<V> rightNode = cur.r;cur.r = rightNode.l;rightNode.l = cur;rightNode.size = cur.size;cur.size = (cur.l != null ? cur.l.size : 0) + (cur.r != null ? cur.r.size : 0) + 1;return rightNode;}private SBTNode<V> maintain(SBTNode<V> cur) {if (cur == null) {return null;}int leftSize = cur.l != null ? cur.l.size : 0;int leftLeftSize = cur.l != null && cur.l.l != null ? cur.l.l.size : 0;int leftRightSize = cur.l != null && cur.l.r != null ? cur.l.r.size : 0;int rightSize = cur.r != null ? cur.r.size : 0;int rightLeftSize = cur.r != null && cur.r.l != null ? cur.r.l.size : 0;int rightRightSize = cur.r != null && cur.r.r != null ? cur.r.r.size : 0;if (leftLeftSize > rightSize) {cur = rightRotate(cur);cur.r = maintain(cur.r);cur = maintain(cur);} else if (leftRightSize > rightSize) {cur.l = leftRotate(cur.l);cur = rightRotate(cur);cur.l = maintain(cur.l);cur.r = maintain(cur.r);cur = maintain(cur);} else if (rightRightSize > leftSize) {cur = leftRotate(cur);cur.l = maintain(cur.l);cur = maintain(cur);} else if (rightLeftSize > leftSize) {cur.r = rightRotate(cur.r);cur = leftRotate(cur);cur.l = maintain(cur.l);cur.r = maintain(cur.r);cur = maintain(cur);}return cur;}private SBTNode<V> add(SBTNode<V> root, int index, SBTNode<V> cur) {if (root == null) {return cur;}root.size++;int leftAndHeadSize = (root.l != null ? root.l.size : 0) + 1;if (index < leftAndHeadSize) {root.l = add(root.l, index, cur);} else {root.r = add(root.r, index - leftAndHeadSize, cur);}root = maintain(root);return root;}private SBTNode<V> remove(SBTNode<V> root, int index) {root.size--;int rootIndex = root.l != null ? root.l.size : 0;if (index != rootIndex) {if (index < rootIndex) {root.l = remove(root.l, index);} else {root.r = remove(root.r, index - rootIndex - 1);}return root;}if (root.l == null && root.r == null) {return null;}if (root.l == null) {return root.r;}if (root.r == null) {return root.l;}SBTNode<V> pre = null;SBTNode<V> suc = root.r;suc.size--;while (suc.l != null) {pre = suc;suc = suc.l;suc.size--;}if (pre != null) {pre.l = suc.r;suc.r = root.r;}suc.l = root.l;suc.size = suc.l.size + (suc.r == null ? 0 : suc.r.size) + 1;return suc;}private SBTNode<V> get(SBTNode<V> root, int index) {int leftSize = root.l != null ? root.l.size : 0;if (index < leftSize) {return get(root.l, index);} else if (index == leftSize) {return root;} else {return get(root.r, index - leftSize - 1);}}public void add(int index, V num) {SBTNode<V> cur = new SBTNode<V>(num);if (root == null) {root = cur;} else {if (index <= root.size) {root = add(root, index, cur);}}}public V get(int index) {SBTNode<V> ans = get(root, index);return ans.value;}public void remove(int index) {if (index >= 0 && size() > index) {root = remove(root, index);}}public int size() {return root == null ? 0 : root.size;}}// 通过以下这个测试,// 可以很明显的看到LinkedList的插入、删除、get效率不如SbtList// LinkedList需要找到index所在的位置之后才能插入或者读取,时间复杂度O(N)// SbtList是平衡搜索二叉树,所以插入或者读取时间复杂度都是O(logN)public static void main(String[] args) {// 功能测试int test = 50000;int max = 1000000;boolean pass = true;ArrayList<Integer> list = new ArrayList<>();SbtList<Integer> sbtList = new SbtList<>();for (int i = 0; i < test; i++) {if (list.size() != sbtList.size()) {pass = false;break;}if (list.size() > 1 && Math.random() < 0.5) {int removeIndex = (int) (Math.random() * list.size());list.remove(removeIndex);sbtList.remove(removeIndex);} else {int randomIndex = (int) (Math.random() * (list.size() + 1));int randomValue = (int) (Math.random() * (max + 1));list.add(randomIndex, randomValue);sbtList.add(randomIndex, randomValue);}}for (int i = 0; i < list.size(); i++) {if (!list.get(i).equals(sbtList.get(i))) {pass = false;break;}}System.out.println("功能测试是否通过 : " + pass);// 性能测试test = 500000;list = new ArrayList<>();sbtList = new SbtList<>();long start = 0;long end = 0;start = System.currentTimeMillis();for (int i = 0; i < test; i++) {int randomIndex = (int) (Math.random() * (list.size() + 1));int randomValue = (int) (Math.random() * (max + 1));list.add(randomIndex, randomValue);}end = System.currentTimeMillis();System.out.println("ArrayList插入总时长(毫秒) : " + (end - start));start = System.currentTimeMillis();for (int i = 0; i < test; i++) {int randomIndex = (int) (Math.random() * (i + 1));list.get(randomIndex);}end = System.currentTimeMillis();System.out.println("ArrayList读取总时长(毫秒) : " + (end - start));start = System.currentTimeMillis();for (int i = 0; i < test; i++) {int randomIndex = (int) (Math.random() * list.size());list.remove(randomIndex);}end = System.currentTimeMillis();System.out.println("ArrayList删除总时长(毫秒) : " + (end - start));start = System.currentTimeMillis();for (int i = 0; i < test; i++) {int randomIndex = (int) (Math.random() * (sbtList.size() + 1));int randomValue = (int) (Math.random() * (max + 1));sbtList.add(randomIndex, randomValue);}end = System.currentTimeMillis();System.out.println("SbtList插入总时长(毫秒) : " + (end - start));start = System.currentTimeMillis();for (int i = 0; i < test; i++) {int randomIndex = (int) (Math.random() * (i + 1));sbtList.get(randomIndex);}end = System.currentTimeMillis();System.out.println("SbtList读取总时长(毫秒) : " + (end - start));start = System.currentTimeMillis();for (int i = 0; i < test; i++) {int randomIndex = (int) (Math.random() * sbtList.size());sbtList.remove(randomIndex);}end = System.currentTimeMillis();System.out.println("SbtList删除总时长(毫秒) : " + (end - start));}}红黑树的基本概念
1)AVL树它的平衡性来自于左树及右树的高度差小于等于1
2)SB树任何一个叔叔节点的个数不小于侄子节点,保证节点较少的树和节点较大的树的数量不超过两倍以上
红黑树定义
1)每个节点不是红就是黑
2)整棵树的头节点一定是黑,叶节点也一定为黑
3)节点有黑有红的情况下两个红节点不能相邻
4)每一颗子树任何一条链黑节点的数量要一样
最长的链条一定是红黑相间的,最短的链一定是只有黑节点的,且长度不会超过两倍以上。此优点是防止像AVL树一样删除和增加节点的时候就马上调整平衡性。对于硬盘的IO消耗比较低
插入有5种情况,删除有8种情况。
相关文章:

有序表常见题型
给定一个数组arr和两个整数a和b求arr中有多少个子数组累加和在a到b这个范围上返回达标的子数组数量 如【3,6,1,9,2】达标的子数组通过暴力求解的方式时间复杂度为O(N的三次方)【找每个子数组占用O…...
【开源】基于JAVA语言的桃花峪滑雪场租赁系统
项目编号: S 036 ,文末获取源码。 \color{red}{项目编号:S036,文末获取源码。} 项目编号:S036,文末获取源码。 目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 游客服务2.2 雪场管理 三、数据库设…...

【开源】基于Vue.js的图书管理系统
文末获取源码,项目编号: S 066 。 \color{red}{文末获取源码,项目编号:S066。} 文末获取源码,项目编号:S066。 目录 一、 系统介绍二、 功能模块2.1 登录注册模块2.1 图书馆模块2.2 图书类型模块2.3 图书模…...
)
python跑ncnn(验证模型是否转换成功)
为了转ncnn模型是否成功,用python验证一下先 pip install ncnn分割模型的验证代码 import ncnn import cv2 import numpy as np# 创建ncnn的网络对象 net ncnn.Net()# 加载ONNX模型 net.load_param(E:\\Android_Projects\\ncnn-android-deeplabv3plus-main\\app\…...

FL Studio 21.2.1.3859中文破解激活版2024免费下载安装图文教程
FL Studio 21.2.1.3859中文破解激活版是我见过更新迭代最快的宿主软件,没有之一。FL Studio12、FL Studio20、FL Studio21等等。有时甚至我刚刚下载好了最新版本,熟悉了新版本一些好用的操作,Fl Studio就又推出了更新的版本,而且F…...
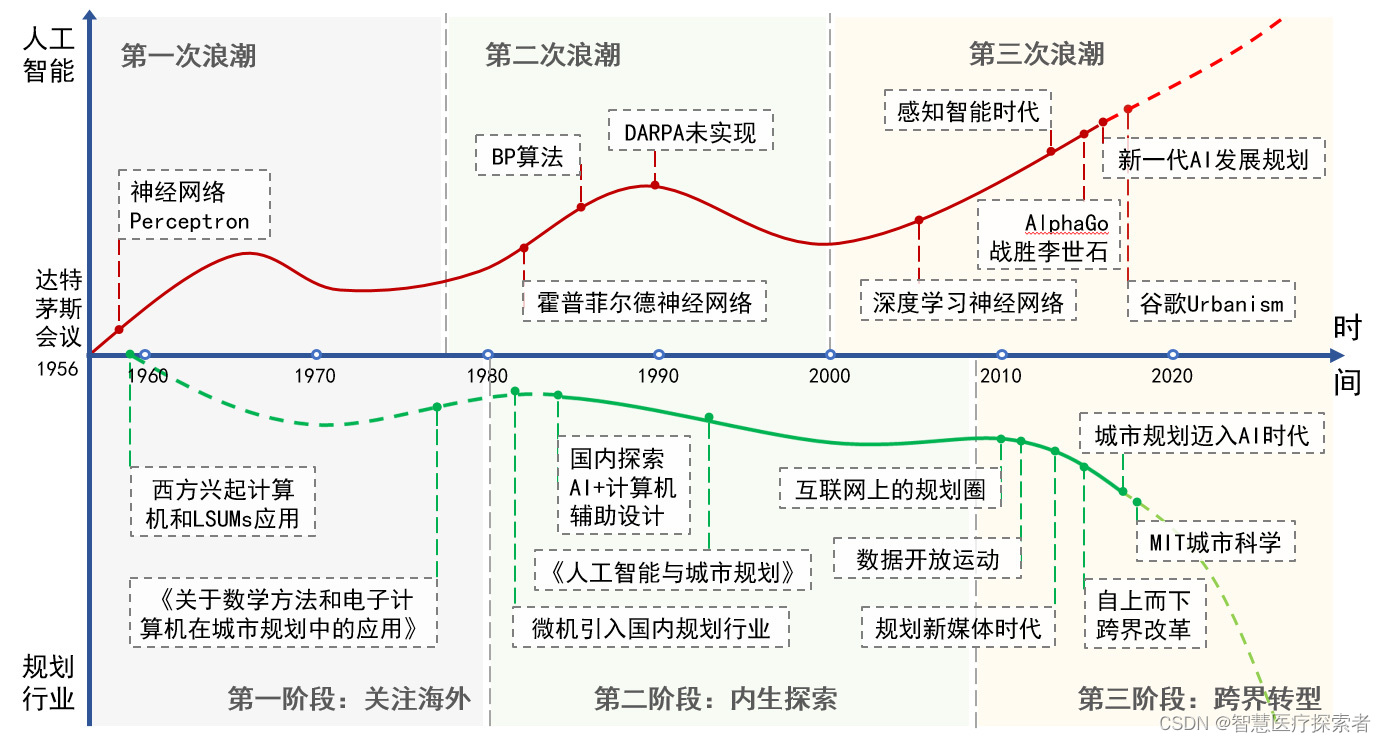
人工智能发展史
人工智能(AI)的发展史是一段跨越数十年的旅程,涵盖了从早期理论探索到现代技术革新的广泛内容。人工智能的发展历程展示了从最初的概念探索到现代技术突破的演变。尽管经历了多次起伏,但AI领域持续进步,不断拓展其应用…...

【面试经典 150 | 二分查找】搜索插入位置
文章目录 写在前面Tag题目来源题目解读解题思路方法一:二分查找闭区间左闭右开区间开区间总结 知识总结写在最后 写在前面 本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更…… 专栏内容以分析题目为主,…...

DAPP开发【06】nodejs安装与npm路径更换
windows系统在执行用户命令时顺序 windows系统在执行用户命令时,若用户未给出文件的绝对路径, 则 (1)首先在当前目录下寻找相应的可执行文件、批处理文件等; (2)若找不到,再依次在系…...
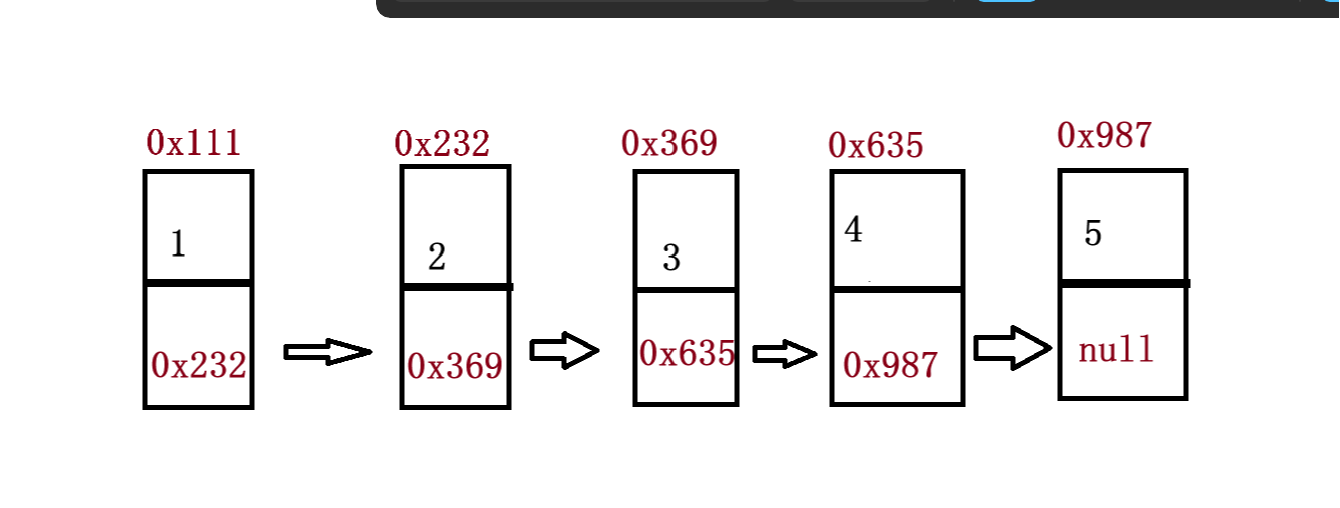
数据结构奇妙旅程之顺序表和链表
꒰˃͈꒵˂͈꒱ write in front ꒰˃͈꒵˂͈꒱ ʕ̯•͡˔•̯᷅ʔ大家好,我是xiaoxie.希望你看完之后,有不足之处请多多谅解,让我们一起共同进步૮₍❀ᴗ͈ . ᴗ͈ აxiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客 本文由xiaoxieʕ̯•͡˔•̯᷅ʔ 原创 CSDN …...
vitepress的使用
创建项目并启动项目 // 1.创建项目,直接在空项目下安装vitepress(npm/yarn等都可以,这个可以看官网,官网给了好几种安装方式) yarn add -D vitepress // 2.初始化配置项目(npm/官网也给了多种包管理工具的安装方式) npx vitepress init // 初始化命令执行完会遇到以下几个问题…...

Discuz论坛自动采集发布软件
随着网络时代的不断发展,Discuz论坛作为一个具有广泛用户基础的开源论坛系统,其采集全网文章的技术也日益受到关注。在这篇文章中,我们将专心分享通过输入关键词实现Discuz论坛的全网文章采集,同时探讨采集过程中伪原创的发布方法…...

B树在数据库的应用
B树(B-tree)是一种自平衡的树状数据结构,广泛应用于数据库和文件系统等领域,其设计的目标是提供一种高效的插入、删除和查找操作。B树的设计是为了在磁盘等存储介质上存储和操作大量的数据。 主要特点包括: 平衡性&a…...

Android 源码编译
一,虚拟机安装 1.1 进入https://cn.ubuntu.com/download中文官网下载iso镜像 1.2 这里我们下载Ubuntu 18.04 LTS 1.3虚拟VM机安装ubuntu系统,注意编译源码需要至少16G运行内存和400G磁盘空间,尽量设大点 二 配置编译环境 2.1 下载andr…...

信而泰 SSL测试方法介绍
[本文介绍在ALPS平台上进行SSL测试的内容和方法] 什么是SSL SSL全称是Secure Sockets Layer,指安全套接字协议,为基于TCP的应用层协议提供安全连接;SSL介于TCP/IP协议栈的第四层和第五层之间,广泛用于电子商务、网上银行等。 SSL…...
Redis--15--缓存穿透 击穿 雪崩
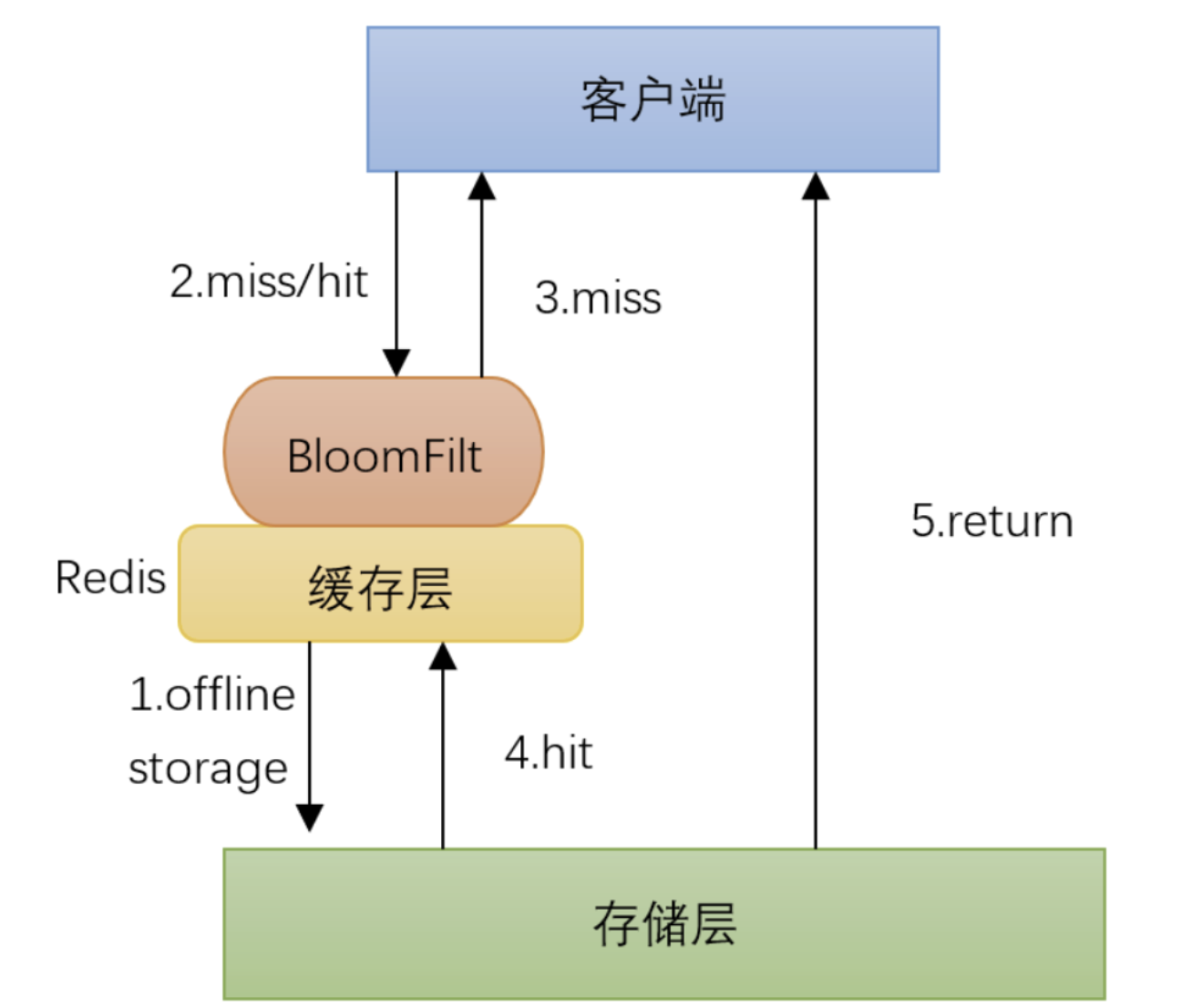
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 缓存穿透 击穿 雪崩运行速度:1 缓存穿透问题描述:如何解决: 2 缓存击穿问题描述:如何解决: 3 缓存雪崩说明:解决方案: 缓存穿透 击穿 雪崩 问题描述: 由于海量的用…...
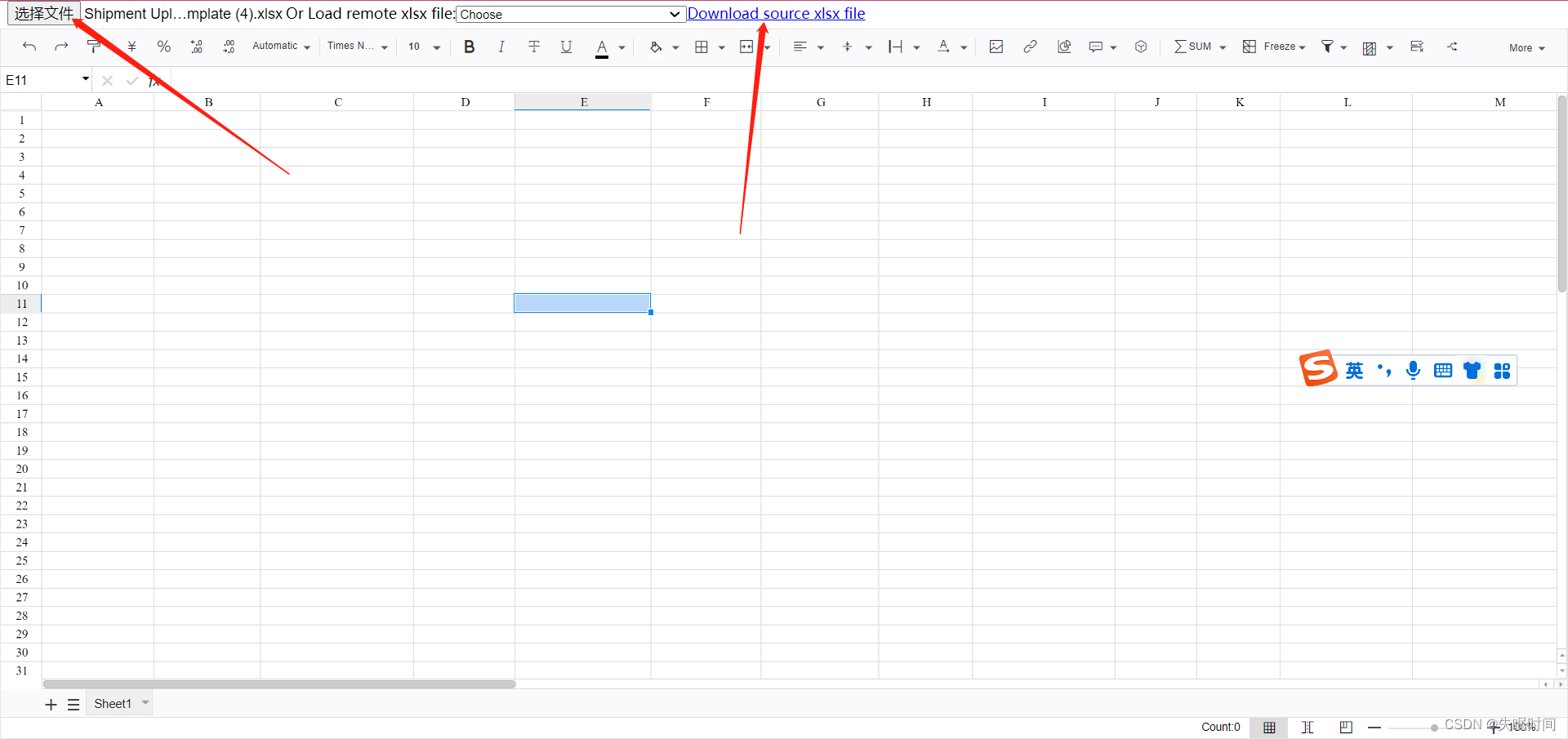
excel表格在线编辑(开源版)
文章目录 前言一、Luckysheetvue3vite 例子如有启发,可点赞收藏哟~ 前言 本文记录好用的开源在线表格 具体如图显示 另外记录下更名后的univer~,如下图(有兴趣可自行详细了解) univer 在线思维导图 一、Luckysheet 参考git…...

17.字符串处理函数——字符串比较函数
文章目录 前言一、题目描述 二、解题 程序运行代码 总结 前言 本系列为字符串处理函数编程题,点滴成长,一起逆袭。 一、题目描述 二、解题 程序运行代码 #include<stdio.h> #include<string.h> int main() {char *str1 "hello wo…...

【面试HOT200】二叉树——深度优先搜索篇
系列综述: 💞目的:本系列是个人整理为了秋招面试的,整理期间苛求每个知识点,平衡理解简易度与深入程度。 🥰来源:材料主要源于【CodeTopHot200】进行的,每个知识点的修正和深入主要参…...

价值投资选股的方法
价值投资法是一种长期投资策略,其核心思想是寻找被市场低估的股票,即股票的市场价格低于其内在价值。这种策略认为,投资者应该关注公司的基本面,如盈利能力、成长潜力、财务状况等,而不是短期的市场波动。以下是价值投…...

java中如何将mysql里面的数据取出来然后通过stream流的方式进行数据处理代码实例?
在 Java 中使用 Stream 流的方式从 MySQL 数据库中取出数据并进行处理,你可以通过 JDBC(Java Database Connectivity)来实现。下面是一个简单的代码示例: import java.sql.*; import java.util.stream.Stream; public class MySQ…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

车载诊断架构 --- ZEVonUDS(J1979-3)简介第一篇
我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 做到欲望极简,了解自己的真实欲望,不受外在潮流的影响,不盲从,不跟风。把自己的精力全部用在自己。一是去掉多余,凡事找规律,基础是诚信;二是…...
 ----- Python的类与对象)
Python学习(8) ----- Python的类与对象
Python 中的类(Class)与对象(Object)是面向对象编程(OOP)的核心。我们可以通过“类是模板,对象是实例”来理解它们的关系。 🧱 一句话理解: 类就像“图纸”,对…...
