【数据结构】拆分详解 - 二叉树的链式存储结构
文章目录
- 一、前置说明
- 二、二叉树的遍历
- 1. 前序、中序以及后序遍历
- 1.1 前序遍历
- 1.2 中序遍历
- 1.3 后序遍历
- 2. 层序遍历
- 三、常见接口实现
- 0. 递归中的分治思想
- 1. 查找与节点个数
- 1.1 节点个数
- 1.2 叶子节点个数
- 1.3 第k层节点个数
- 1.4 查找值为x的节点
- 2. 二叉树的创建与销毁
- 2.1 创建
- 2.2 销毁
- 总结
一、前置说明
在学习二叉树的基本操作前,需先要创建一棵二叉树,然后才能学习其相关的基本操作。由于现在大家对二叉树结构掌握还不够深入,为了降低大家学习成本,此处手动快速创建一棵简单的二叉树,快速进入二叉树操作学习,等二叉树结构了解的差不多时,我们反过头再来研究二叉树真正的创建方式。
注意:下述代码并不是创建二叉树的方式,真正创建二叉树方式文章末尾处会进行讲解。
typedef int BTDataType;
typedef struct BinaryTreeNode
{BTDataType _data;struct BinaryTreeNode* _left;struct BinaryTreeNode* _right;
}BTNode;BTNode* CreatBinaryTree()
{BTNode* node1 = BuyNode(1);BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode * node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);node1->_left = node2;node1->_right = node4;node2->_left = node3;node4->_left = node5;node4->_right = node6;return node1;
}
二、二叉树的遍历
1. 前序、中序以及后序遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉树中的所有节点进行访问。
按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历,区别为访问根的顺序不同。
- 前序遍历 :访问顺序为根,左子树,右子树
- 中序遍历:访问顺序为左子树,根,右子树
- 后序遍历:访问顺序为左子树,右子树,根
1.1 前序遍历
void BinaryTreePrevOrder(BTNode* root)
{//为空if (root == NULL){printf("N ");return ;}//不为空,打印节点值,继续找左子树,找完后找右子树printf("%d ", root->data);BinaryTreePrevOrder(root->left);BinaryTreePrevOrder(root->right);
}
1.2 中序遍历
void BinaryTreeInOrder(BTNode* root)
{//为空if (root == NULL){printf("N ");return;}//左BinaryTreeInOrder(root->left);//根printf("%d ", root->data);//右BinaryTreeInOrder(root->right);
}
1.3 后序遍历
void BinaryTreePostOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}BinaryTreePostOrder(root->left);BinaryTreePostOrder(root->right);printf("%d ", root->data);
}
2. 层序遍历
除了先序遍历、中序遍历、后序遍历外,还可以对二叉树进行层序遍历。设二叉树的根节点所在层数为1,层序遍历就是从所在二叉树的根节点出发,首先访问第一层的树根节点,然后从左到右访问第2层上的节点,接着是第三层的节点,以此类推,自上而下,自左至右逐层访问树的结点的过程就是层序遍历。
三、常见接口实现
0. 递归中的分治思想
在下面的接口实现中我们使用递归实现分治思想(将大问题拆分成多个子问题处理),我们要注意如何拆分子问题 和 表达递归的结束条件。
- 递归:分为递推和回归。我们可以画递推展开图,假想递推到底的情况,思考分析回归条件,可代入回归检验是否符合。
- 分治:将问题抽象分为多个子问题,分别解决
- 用递归实现分治 :一路递推到底,处理完第一个子问题,回归,在回归过程中处理之前未处理的子问题。(子问题可能会被处理多次,但每个子问题的处理次数总和一定是相同的,只是处理先后的不同)本质是将问题的核心基础步骤抽象出来,使用递归方式重复处理,最终达成目的。
1. 查找与节点个数
1.1 节点个数
子问题分治:节点个数 = 左子树节点个数 + 右子树节点个数
递归(结束)返回条件:
- 空 返回 0
- 不为空 返回1
int BinaryTreeSize(BTNode* root)
{//如果根为空就返回0,否则返回左子树与右子树节点数和return root == NULL ? 0 : BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}
1.2 叶子节点个数
子问题分治:节点个数 = 左子树叶子节点个数 + 右子树叶子节点个数
递归(结束)返回条件:
- 空 返回 0
- 叶子 返回1
int BinaryTreeLeafSize(BTNode* root)
{//单独判断空树if (root == NULL){return 0;}//如果左子树和右子树都不为空,说明为叶子if (!root->left && !root->right){return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
1.3 第k层节点个数
子问题分治:第k层节点个数 = 第k-1层的左子树节点个数 + 第k-1层的右子树节点个数
递归(结束)返回条件:
- 空 返回 0
- 不为空且为k层 返回1
int BinaryTreeLevelKSize(BTNode* root, int k)
{assert(k> 0);if (root == NULL)return 0;//不为空且为k层,返回1if (k == 1)return 1;//k == 1 说明为k层,不为则继续向下递推return BinaryTreeLevelKSize(root->left, k-1) + BinaryTreeLevelKSize(root->right, k-1);
}
1.4 查找值为x的节点
子问题分治:查找 = 查找左子树 + 查找右子树
递归(结束)返回条件:
- 空 返回 0
- 找到 返回节点地址
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)return NULL;if (root->data == x)return root;//使用指针变量存储地址,若不为空说明找到,不需要进行其他操作,使其一路回归BTNode* ret1 = BinaryTreeFind(root->left, x);if (ret1)return ret1;BTNode* ret2 = BinaryTreeFind(root->right, x);if (ret2)return ret2;return NULL;
}
2. 二叉树的创建与销毁
2.1 创建
子问题分治:创建 = 创建左子树 + 创建右子树
递归(结束)返回条件:
- 空(‘#’) 返回NULL
- 非空 创建节点并初始化
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
// a为数组,pi为 外部中标识数组下标变量的 指针
BTNode* BinaryTreeCreate(BTDataType* a, int n, int* pi)
{if (a[*pi] == '#'){*pi++; //下标后移return NULL;}BTNode* root = (BTNode*)malloc(sizeof(BTNode));if (root == NULL){perror("malloc fail");exit(-1);}root->data = a[*pi];root->left = BinaryTreeCreate(a, n, ++*pi);root->right = BinaryTreeCreate(a, n, ++ * pi);
}
2.2 销毁
void BinaryTreeDestory(BTNode** root)
{if (*root == NULL){return;}BinaryTreeDestory((*root)->left);free(*root);BinaryTreeDestory((*root)->right);free(*root);free(*root);*root == NULL;
}
总结
知识框架可看文章目录。
本文讲解了二叉树的链式存储结构的相关知识,递归和分治思想十分抽象,需要读者自行画递归展开图理解,多练习,培养出自己的抽象能力。
文章中有什么不对的丶可改正的丶可优化的地方,欢迎各位来评论区指点交流,博主看到后会一一回复。
相关文章:

【数据结构】拆分详解 - 二叉树的链式存储结构
文章目录 一、前置说明二、二叉树的遍历 1. 前序、中序以及后序遍历 1.1 前序遍历 1.2 中序遍历 1.3 后序遍历 2. 层序遍历 三、常见接口实现 0. 递归中的分治思想 1. 查找与节点个数 1.1 节点个数 1.2 叶子节点个数 1.3 第k层节…...
验证)
Laravel修改默认的auth模块为md5(password+salt)验证
首先声明:这里只是作为一个记录,实行拿来主义,懒得去记录那些分析源码的过程,不喜勿喷,可直接划走。 第一步:创建文件夹:app/Helpers/Hasher; 第二步:创建文件: app/Help…...

OpenStack-train版安装之安装Keystone(认证服务)、Glance(镜像服务)、Placement
安装Keystone(认证服务)、Glance(镜像服务)、Placement 安装Keystone(认证服务)安装Glance(镜像服务)安装Placement 安装Keystone(认证服务) 数据库创建、创…...

【九日集训】第九天:简单递归
递归就是自己调用自己,例如斐波那契数列就是可以用简单递归来实现。 第一题 172. 阶乘后的零 https://leetcode.cn/problems/factorial-trailing-zeroes/description/ 这一题纯粹考数学推理能力,我这种菜鸡看了好久都没有懂。 大概是这样的思路&#x…...
Prime 1.0
信息收集 存活主机探测 arp-scan -l 或者利用nmap nmap -sT --min-rate 10000 192.168.217.133 -oA ./hosts 可以看到存活主机IP地址为:192.168.217.134 端口探测 nmap -sT -p- 192.168.217.134 -oA ./ports UDP端口探测 详细服务等信息探测 开放端口22&#x…...

Java 如何正确比较两个浮点数
看下面这段代码,将 d1 和 d2 两个浮点数进行比较,输出的结果会是什么? double d1 .1 * 3; double d2 .3; System.out.println(d1 d2);按照正常逻辑来看,d1 经过计算之后的结果应该是 0.3,最后打印的结果应该是 tru…...
Qt 如何操作SQLite3数据库?数据库创建和表格的增删改查?
# 前言 项目源码下载 https://gitcode.com/m0_45463480/QSQLite3/tree/main # 第一步 项目配置 平台:windows10 Qt版本:Qt 5.14.2 在.pro添加 QT += sql 需要的头文件 #include <QSqlDatabase>#include <QSqlError>#include <QSqlQuery>#include &…...
【Hadoop】分布式文件系统 HDFS
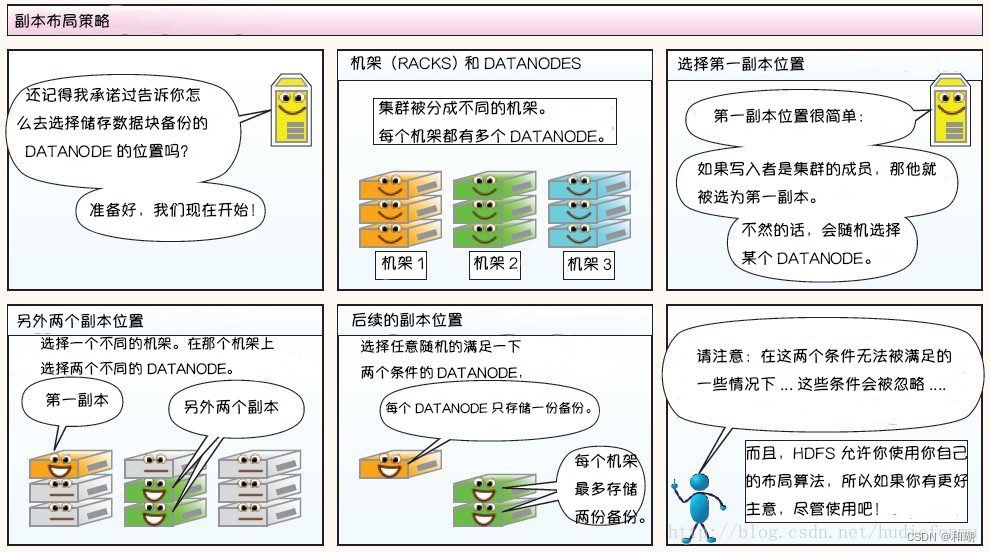
目录 一、介绍二、HDFS设计原理2.1 HDFS 架构2.2 数据复制复制的实现原理 三、HDFS的特点四、图解HDFS存储原理1. 写过程2. 读过程3. HDFS故障类型和其检测方法故障类型和其检测方法读写故障的处理DataNode 故障处理副本布局策略 一、介绍 HDFS (Hadoop Distribute…...

【Python-随笔】使用Python实现屏幕截图
使用Python实现屏幕截图 环境配置 下载pyautogui包 pip install pyautogui -i https://pypi.tuna.tsinghua.edu.cn/simple/下载OpenCV包 pip install opencv-python -i https://pypi.tuna.tsinghua.edu.cn/simple/下载PyQT5包 pip install PyQt5 -i https://pypi.tuna.tsi…...

Sun Apr 16 00:00:00 CST 2023格式转换
Date date new Date(); log.info("当前时间为:{}",date); //yyyy-MM-dd HH:mm:ss SimpleDateFormat sdf new SimpleDateFormat(DateUtils.YYYY_MM_DD_HH_MM_SS); String dateTime s…...

使用mongodb实现简单的读写操作
本文适合初学者,特别是刚刚安装了mongodb数据库的朋友,或在atlas刚拿到免费集群的朋友。 拿到数据库,心情很激动,手痒难耐。特别想向数据库插入几条数据库试试。即使是深夜完成了安装,也忍不住想去完成这些操作。看到…...

C语言实现Cohen_Sutherland算法
前提简要: 算法简介: 编码算法是最早、最流行的线段裁剪算法,该算法采用区域检验的方法,能够快速有效地判断一条线段与裁剪窗口的位置关系,对完全接受或完全舍弃的线段无需求交,即可直接识别。 算法思想&…...

MySQL进阶_EXPLAIN重点字段解析
文章目录 第一节.准备1.1 版本信息1.2 准备 第二节.type2.1 system2.2 const2.3 eq_ref2.4 ref2.5 ref_or_null2.6 index_merge2.7 unique_subquery2.8 range2.9 index2.10 all 第三节. Extra3.1 No tables used3.2 No tables used3.3 Using where3.4 No matching min/max row3…...
视图层与模板层
视图层 1 视图函数 一个视图函数,简称视图,是一个简单的Python 函数,它接受Web请求并且返回Web响应。响应可以是一张网页的HTML内容,一个重定向,一个404错误,一个XML文档,或者一张图片. . . 是…...
)
MySQL数据库——触发器-案例(Insert类型、Update类型和Delete类型)
目录 表结构准备 插入数据触发器 代码 测试 修改数据触发器 代码 测试 删除数据触发器 代码 测试 通过触发器记录 tb_user 表的数据变更日志,将变更日志插入到日志表user_logs中,包含增加,修改,删除。 表结构准备 根据…...
)
快速创建桌面端(electron-egg)
介绍 | electron-egg electron-egg: 一个入门简单、跨平台、企业级桌面软件开发框架。 electron-egg是一个基于Electron和Egg.js的框架,可以用于快速构建跨平台的桌面应用程序。 1.兼容平台:electron-egg可以在Windows、MacOS和Linux等多个平台上运行…...

docker配置redis插件
docker配置redis插件 运行容器redis_6390 docker run -it \ --name redis_6390 \ --privileged \ -p 6390:6379 \ --network wn_docker_net \ --ip 172.18.12.19 \ --sysctl net.core.somaxconn1024 \ -e TIME_ZONE"Asia/Shanghai" -e TZ"Asia/Shanghai"…...
前端入口教程_web01
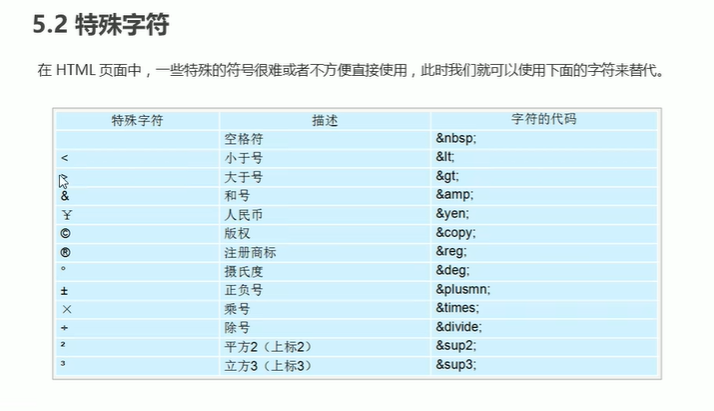
web标准 记得看! html:表示整个页面 head: titile: body: 常用标签 1.标题标签 2.段落标签 3.换行标签 4.文本格式化标签 5. 和 标签 6.图像标签 相对路径–用来插自己本地的图片 #### 绝对路径–用来插网上找的图…...
Win7 SP1 x64 Google Chrome 字体模糊
1 打开 Google Chrome ,地址栏输入 chrome://version/ ,字体模糊。 2 Microsoft Update Catalog 搜索更新 kb2670838,下载,安装,重启电脑。 3 打开 Google Chrome,地址栏输入 chrome://version/ ࿰…...
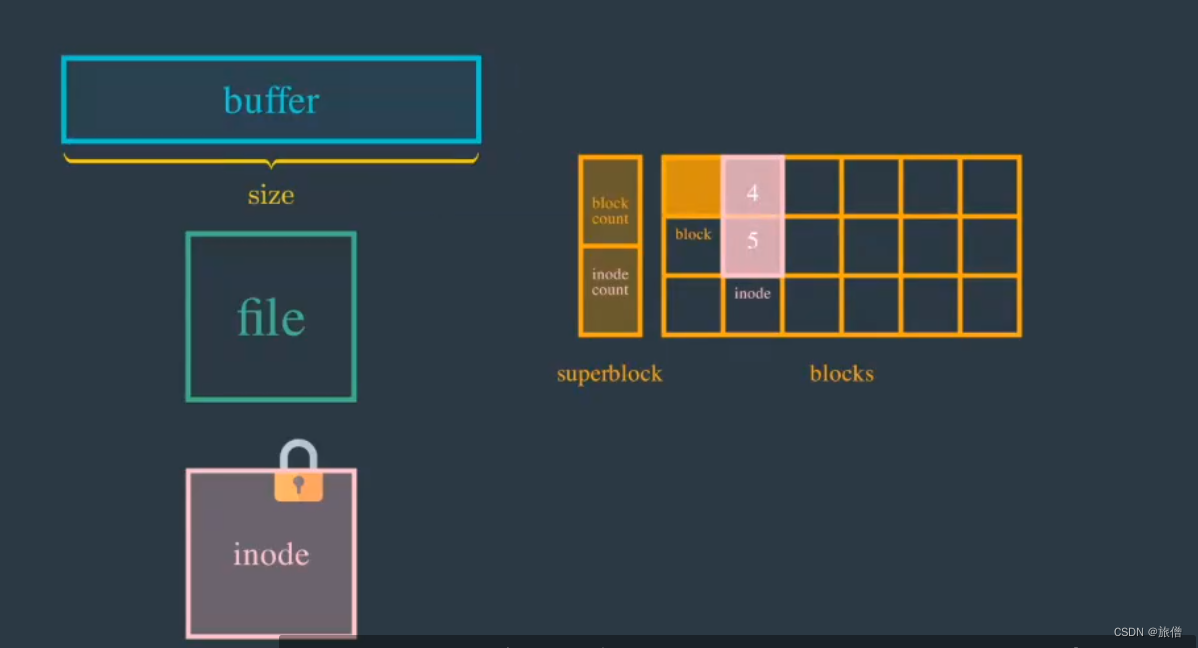
read()之后操作系统都干了什么
首先说明三个参数 file文件 buff从内存中开辟一段缓冲区用来接收读取的数据 size表示这个缓冲区的大小 有关file的参数: 状态:被打开 被关闭权限:可读可写最重要的是inode: 他包含了 文件的元数据(比如文件大小 文件类型 文件在访问前需要加…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...
