B树你需要了解一下
- 介绍
- B树的度数
- 主要特点
- 应用场景
- 时间复杂度
- 代码示例
- 拓展
介绍
B树(B-tree)是一种自平衡的树,能够保持数据有序,常被用于数据库和文件系统的实现。
B树可以看作是一般化的二叉查找树,它允许拥有多于2个子节点。与自平衡二叉查找树不同,B树为系统大块数据的读写操作进行了优化。B树减少定位记录时所经历的中间过程,从而加快存取速度。这种数据结构可以用来描述外部存储,这种数据结构常被应用在数据库和文件系统的实现上。
B树的度数
B树的度数是指每个节点(除根节点和叶子节点外)的关键字数量。在B树中,每个节点(除根节点和叶子节点外)至少包含t-1个关键字,其中t是B树的度数。这些关键字被存储在一个数组中,并且按照从小到大的顺序排列。每个关键字的左子树中的所有关键字都小于它,而右子树中的所有关键字都大于它。因此,对于一个给定的B树,它的度数t决定了每个节点中的关键字数量和B树的平衡性。
主要特点
- 所有叶子节点在同一高度上,且不携带信息(即绝对平衡)。
- 每个节点都存有索引和数据,也就是对应的key和value。
- 每个结点中的关键字都按照从小到大的顺序排列,每个关键字的左子树中的所有关键字都小于它,而右子树中的所有关键字都大于它。
- B树在相同的磁盘块上保持相关(即具有相似键值的记录),这有助于最大限度地减少由于参考位置引起的搜索磁盘I/O。
- B树保证树中的每个节点中值的数量至少满足一定的最小百分比。 这样可以提高空间效率,同时减少在搜索或更新操作过程中所需的典型磁盘数量。
- 更新和查找操作仅仅影响到很少的磁盘块。
在实际应用中,B树常被用于数据库和文件系统的实现,以优化系统大块数据的读写操作。
应用场景
B树的应用场景主要包括数据库和文件系统。它的设计思想是将相关数据尽量集中在一起,以便一次读取多个数据,减少硬盘操作次数。B树算法能够减少定位记录时所经历的中间过程,从而加快存取速度。因此,B树非常适合用于对大量数据进行快速查找、插入、删除等操作。
在数据库系统中,B树常被用于索引的实现,以提高查询效率。在文件系统中,B树则常被用于文件目录的管理,以实现对文件的快速访问和操作。此外,B树还可以用于实现其他需要高效查找和访问数据的应用场景,如搜索引擎、内存管理等。
很多搜索引擎也使用B树或者B+树作为后排索引,因为B树的结构非常适合处理大规模的数据集。此外,B树也常用于内存管理,可以作为内存中的排序结构。
B树的应用场景非常广泛,只要是需要对大量数据进行高效查找、插入、删除等操作的地方,都可以考虑使用B树。
时间复杂度
B树的查询、插入和删除操作的时间复杂度都是O(logn),其中n是B树中包含的数据记录数量。这个时间复杂度比二叉搜索树(BST)的最差情况时间复杂度O(n)要好得多,因为B树是一种平衡的树,每个节点可以有多个子节点,从而减少了树的高度。在实际应用中,B树常被用于数据库和文件系统的实现,以优化系统大块数据的读写操作。
B树的时间复杂度取决于B树的度数t。在实际情况中,为了获得更好的磁盘读写性能,通常选择适当的t值来平衡树的高度和每个节点的关键字数量。在选择t值时,需要考虑到磁盘块的大小和数据量的大小等因素。
代码示例
以下是使用Java实现一棵B树的示例代码:
class Node {int degree; // B树的度数int[] keys; // 关键字数组Node[] children; // 子节点数组boolean leaf; // 是否为叶子节点public Node(int degree) {this.degree = degree;keys = new int[degree];children = new Node[degree + 1];leaf = false;}
}class BTree {private Node root; // 根节点private int t; // B树的度数public BTree(int t) {this.t = t;root = new Node(t);}// 查找操作public int search(int key) {Node current = root;while (!current.leaf) {int index = 0;while (index < current.degree) {if (key < current.keys[index]) {current = current.children[index];break;} else if (key > current.keys[index]) {index++;} else {return current.keys[index];}}current = current.children[index];}for (int i = 0; i < current.degree; i++) {if (key == current.keys[i]) {return current.keys[i];} else if (key < current.keys[i]) {break;}}return -1; // 没有找到关键字,返回-1表示未找到。可以根据实际需要返回其他值。}// 插入操作,假设B树中不存在重复关键字。插入后,如果根节点超过度数,则分裂根节点。如果插入后导致某个节点超过度数且该节点不是根节点,则分裂该节点。如果分裂后导致根节点成为叶子节点且根节点只有一个关键字,则合并根节点。插入过程中可能需要执行多次分裂和合并操作。代码中只实现了插入操作的基本思路,具体的实现需要根据具体的需求和条件进行调整和优化。public void insert(int key) {Node current = root;while (!current.leaf) {int index = 0;while (index < current.degree) {if (key < current.keys[index]) {current = current.children[index];break;} else if (key > current.keys[index]) {index++;} else { // 如果关键字已经存在于当前节点中,直接返回。可以根据实际需要返回其他值。return; // 如果关键字已经存在于当前节点中,直接返回。可以根据实际需要返回其他值。}}current = current.children[index]; // 插入到当前节点的子节点中。可以根据实际需要返回其他值。
拓展
AVL树你需要了解一下
红黑树你需要了解一下
满二叉树你需要了解一下
完全二叉树你需要了解一下
哈夫曼树你需要了解一下
二叉查找(排序)树你需要了解一下

相关文章:

B树你需要了解一下
介绍B树的度数主要特点应用场景时间复杂度代码示例拓展 介绍 B树(B-tree)是一种自平衡的树,能够保持数据有序,常被用于数据库和文件系统的实现。 B树可以看作是一般化的二叉查找树,它允许拥有多于2个子节点。与自平衡…...

MFC设置状态栏文本导致崩溃的原因
文章目录 问题和原因解决办法1.消息机制2.定时器问题和原因 本人在类A使用多线程执行操作并且调用了类B的设置状态栏文本的函数,导致崩溃 类A void A::distribute_n_start_msg(){((B*)m_parent)->received_msg_n_start...
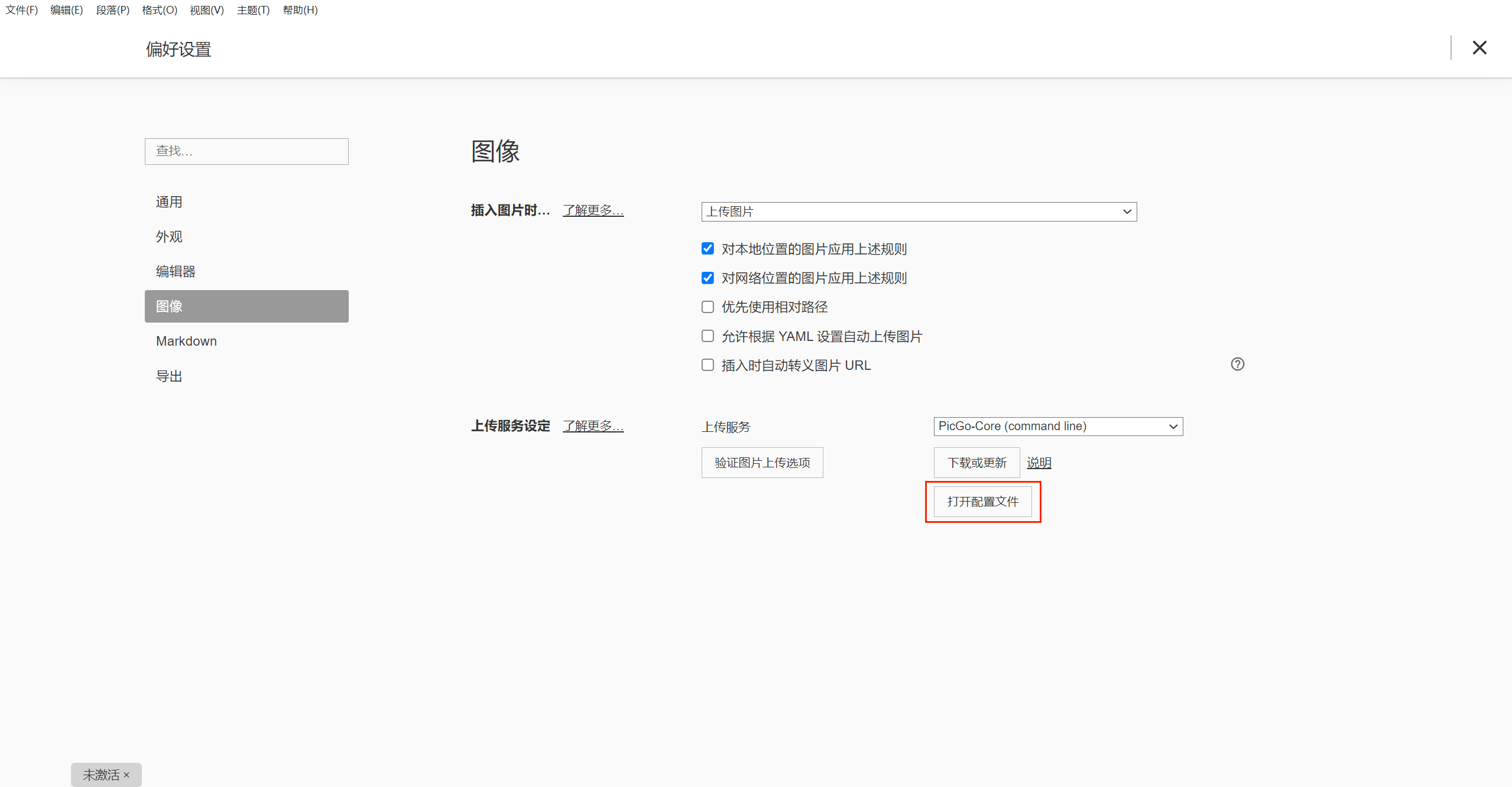
配置typroa上传图片到gitee
一、gitee相关配置 到gitee官网创建一个新的仓库并获取其token gitee配置时候一定要新建仓库之后初始化好仓库 比如:创建出README.md文档 出现master这个显示界面,刚开始未初始化的时候是会报错的 二、typora相关配置 在typora这个位置下载插件 在p…...

java并发-线程生命周期
文章目录 前言状态图状态变化说明补充说明 前言 线程的生命周期指的是线程从创建出来到最终消亡的整个过程,以及过程中的状态变化。 状态图 以下图用mermaid语法绘制: #mermaid-svg-32vKT6KmFdlYvCnr {font-family:"trebuchet ms",verdana,…...
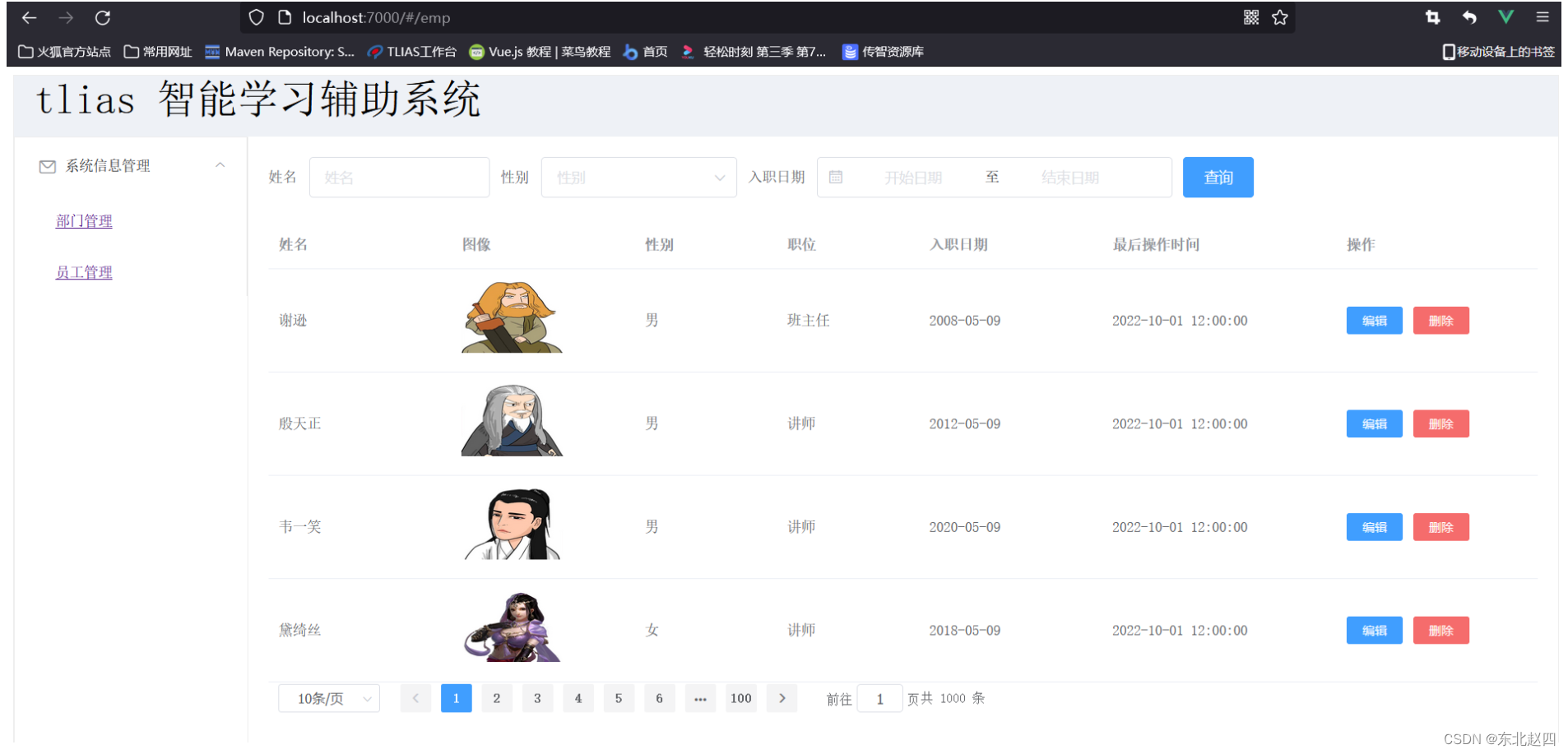
Javaweb之Vue路由的详细解析
5 Vue路由 5.1 路由介绍 将资代码/vue-project(路由)/vue-project/src/views/tlias/DeptView.vue拷贝到我们当前EmpView.vue同级,其结构如下: 此时我们希望基于4.4案例中的功能,实现点击侧边栏的部门管理,显示部门管理的信息&am…...
)
力扣:196. 删除重复的电子邮箱(Python3)
题目: 表: Person ---------------------- | Column Name | Type | ---------------------- | id | int | | email | varchar | ---------------------- id 是该表的主键列(具有唯一值的列)。 该表的每一行包含一封电子邮件。电子邮件将不包含…...

Ruby和HTTParty库下载代码示例
ruby require httparty require nokogiri # 设置服务器 proxy_host "" proxy_port "" # 定义URL url "" # 创建HTTParty对象,并设置服务器 httparty HTTParty.new( :proxy > "#{proxy_host}:#{proxy_port}" ) …...

Unity 使用Horizontal Layout Group和Toggle制作多个水平开关按钮实现自动排列和单个点击放大后的自动排列。
Unity的布局组件Horizontal Layout Group是很好用的,当然也包括其它布局组件也一样好用。 比如要实现多按钮开关自动水平排列,那么就可以使用它了。 首先我们为按钮创建个父物体(我这里使用了Scroll View中的Content作为父物体)…...
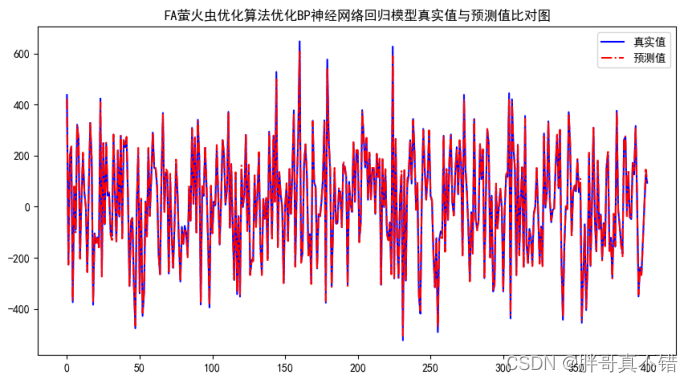
Python实现FA萤火虫优化算法优化BP神经网络回归模型(BP神经网络回归算法)项目实战
说明:这是一个机器学习实战项目(附带数据代码文档视频讲解),如需数据代码文档视频讲解可以直接到文章最后获取。 1.项目背景 萤火虫算法(Fire-fly algorithm,FA)由剑桥大学Yang于2009年提出 , …...

灯塔ARL-NPoC全面教程
灯塔ARL-NPoC全面教程 1.ARL-NPoC2.安装3.参数解析4.ARL-NPoC编写指南标准POC模板`__init()__`verifyexploit_cmd5.将指纹同步到远程Web服务器1.ARL-NPoC 最新版的arl增加了poc编写与探测的功能,ARL-NPoC是一个集漏洞验证和任务运行的一个框架 2.安装 ARL-NPoC下载地址 下载…...
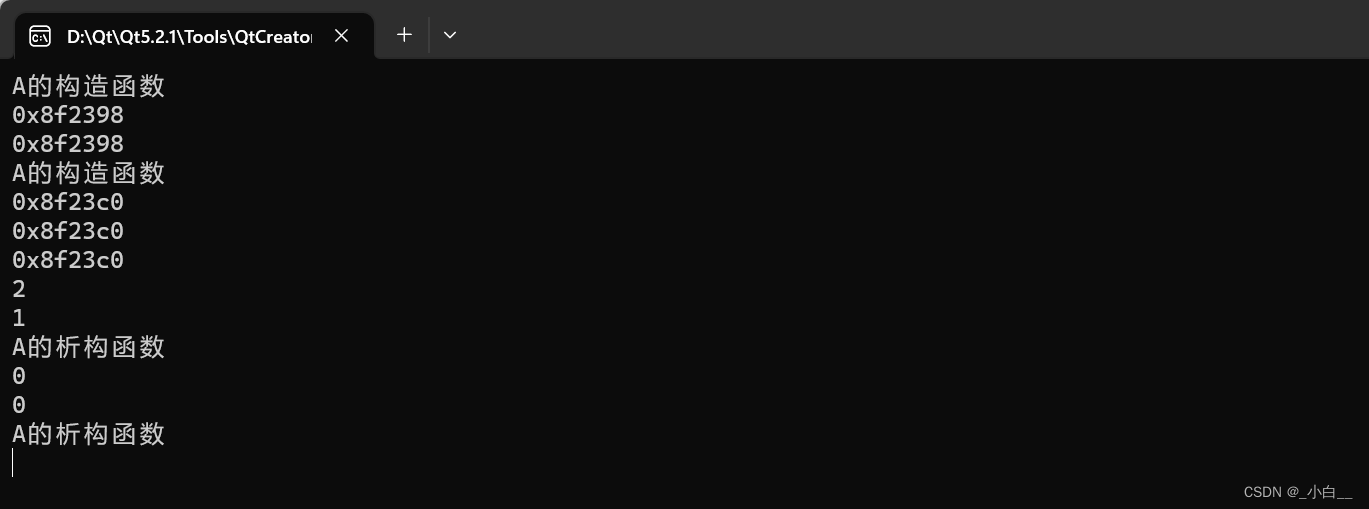
λ表达式、智能指针
lambda 表达式 1、C11标准支持,实现匿名函数的功能; 2、通常用于实现轻量级的函数 格式 mutable->返回值{函数体}; // 返回值即使是 void 也必须得写 [] 内,可以填外部数据; () 内,可以带有参数列表。 lambda 表达…...

PHP基础知识和操作
PHP在线运行 https://c.runoob.com/compile/1/ https://www.sotool.net/php80 将驼峰字符串转化为蛇形字符串 <?phpfunction CamelToSnake($camelValue) {$initValue preg_replace(/\s/u, , $camelValue);$snakeValue strtolower(preg_replace(/(.)(?[A-Z])/u, &quo…...
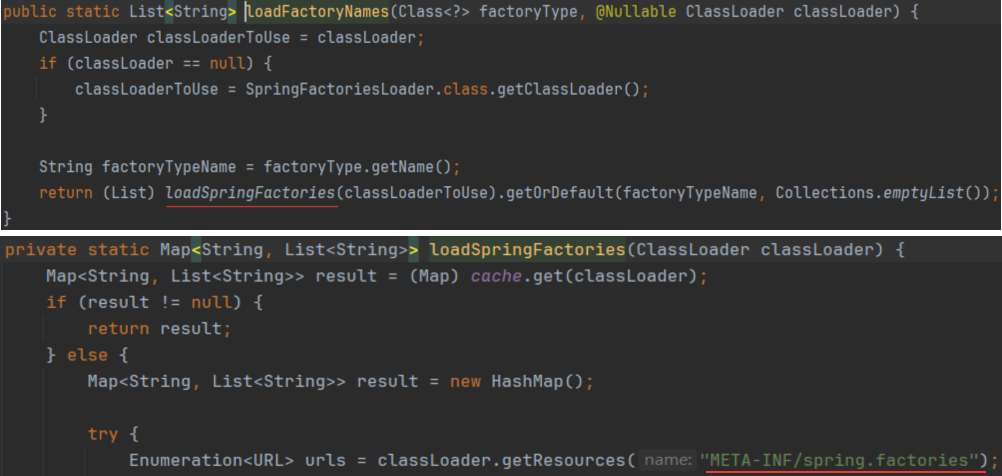
系列十三、SpringBoot的自动配置原理分析
一、概述 我们知道Java发展到现在功能十分的强大,生态异常的丰富,这里面离开不了Spring及其家族产品的支持,而作为Spring生态的明星产品Spring Boot可以说像王者一般的存在,那么的耀眼,那么的光彩夺目!那么…...

soapui报错: CXF directory must be set in global preferences
文章目录 下载官网下载网盘下载 配置 soapui生成代码时报错 CXF directory must be set in global preferences 下载 需要下载apache-cxf。 官网下载 官网地址: https://www.apache.org/dyn/closer.lua/cxf/3.5.4/apache-cxf-3.5.4.zip 点如下地址即可。 The obj…...
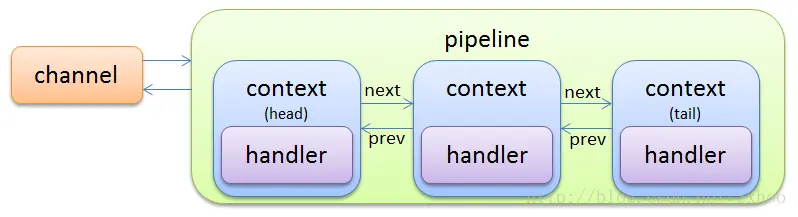
Netty02-基础概念
什么是netty Netty是一个基于Java NIO的异步事件驱动网络应用程序框架。它提供了简单易用的API,用于快速开发可维护的高性能网络应用程序。Netty的设计目标是提供一种高度可扩展的、高性能的网络应用程序框架,使得开发人员能够轻松地构建各种类型的网…...

计算机毕业设计 基于SpringBoot的敬老院管理系统的设计与实现 Java实战项目 附源码+文档+视频讲解
博主介绍:✌从事软件开发10年之余,专注于Java技术领域、Python人工智能及数据挖掘、小程序项目开发和Android项目开发等。CSDN、掘金、华为云、InfoQ、阿里云等平台优质作者✌ 🍅文末获取源码联系🍅 👇🏻 精…...

精调llama模型
github地址:https://github.com/facebookresearch/llama-recipes github:https://github.com/facebookresearch/llama import torch from transformers import LlamaForCausalLM, LlamaTokenizer#model_id"./models_hf/7B" # 可以从huggingface上面下载模…...
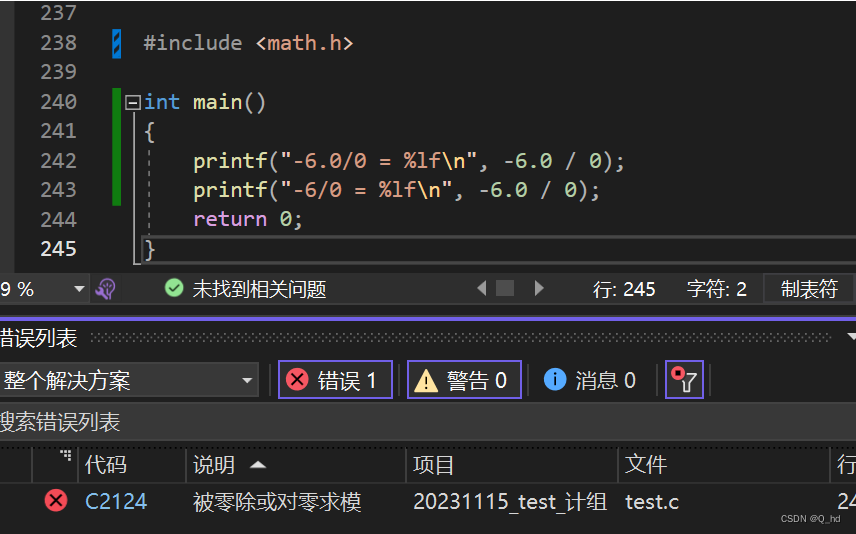
【C语言】深入理解C语言中的数学运算和类型转换
文章目录 引言取负运算的奥秘源码探索分析与解读 浮点数运算的精细差异源码分析精度损失与隐式类型转换 精度和除零运算探究float类型和double类型的精度各是多少(即十进制有效位的位数)?在你的机器上,“负数开方”是如何处理的&a…...
基于javaweb的宠物服务商城系统设计与开发
摘 要 最近几年以来,宠物在人们的日常生活中所占的地位越来越重要了,它们不仅仅是我们的朋友,也成为了我们家庭中的一份子。21世纪,信息技术飞速发展,计算机行业日新月异,极大地带动了信息的流动ÿ…...

LeetCode-470. 用 Rand7() 实现 Rand10()【数学 拒绝采样 概率与统计 随机化】
LeetCode-470. 用 Rand7 实现 Rand10【数学 拒绝采样 概率与统计 随机化】 题目描述:解题思路一:首先说一个结论就是(rand_X() - 1) Y rand_Y() > [1,X*Y],即可以等概率的生成[1, X * Y]范围的随机数,其实就像军训的时候报数…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

云启出海,智联未来|阿里云网络「企业出海」系列客户沙龙上海站圆满落地
借阿里云中企出海大会的东风,以**「云启出海,智联未来|打造安全可靠的出海云网络引擎」为主题的阿里云企业出海客户沙龙云网络&安全专场于5.28日下午在上海顺利举办,现场吸引了来自携程、小红书、米哈游、哔哩哔哩、波克城市、…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...
