11.30BST理解,AVL树操作,定义;快速幂,二分求矩阵幂(未完)
完全二叉树结点的度可能有1,满二叉树的度只能为0或2
BST构建
BST是左孩子都比根节点小,右孩子都比根节点大
二叉搜索树的插入,删除,调整
平衡树理解
任何一个平衡二叉树,它的中序遍历都是一样的,都是有序的从小到大
之所以有调整,就是谁当根节点不同导致的。
作为根节点,就需要提供两个信息,一个是左孩子,一个是右孩子。
那么中序遍历的过程就是,先由根节点向左一直蔓延,直到到底,然后从左到右依次遍历,遍历到根节点,再从根节点向右遍历蔓延。想象一个有序序列,找到任意一个起点,这个起点就是所谓的树的根节点,那么中序遍历就是左根右,即从左到右,就是从起点(根节点)先一直向左,到底后再逐个输出,那就是中序序列。有这样的性质,就是因为左根右,序列中的每个结点左侧都是它的左孩子,它的右侧都是右孩子或者父母结点
即,左侧只会是左孩子,但右侧可能是右孩子或父母节点,但由于左孩子都小于根节点,所以一旦有右孩子,那么只能先是右孩子,即右孩子的优先级大于父母结点,因为右孩子一定小于父母节点。
AVL树
平衡因子是根节点的定义,即根节点的左右孩子高度差
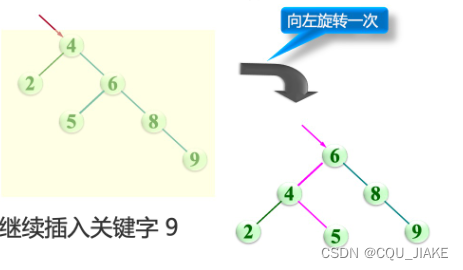
如这里是4的平衡因子不满足条件,其左子树,右子树高度差大于1
求高度函数
typedef struct node {int data;node* lchild, * rchild;
}*tree;
int high(tree root) {if (root) {return max(high(root->lchild), high(root->rchild)) + 1;}return 0;
}AVL树的构建
AVL树的调整
中序遍历都是一样的,不一样的就是根节点的确定,即起点的确定
右旋
右旋的具体步骤:
- T向右旋转成为L的右结点
- L的右节点Y 放到 T的左孩子上
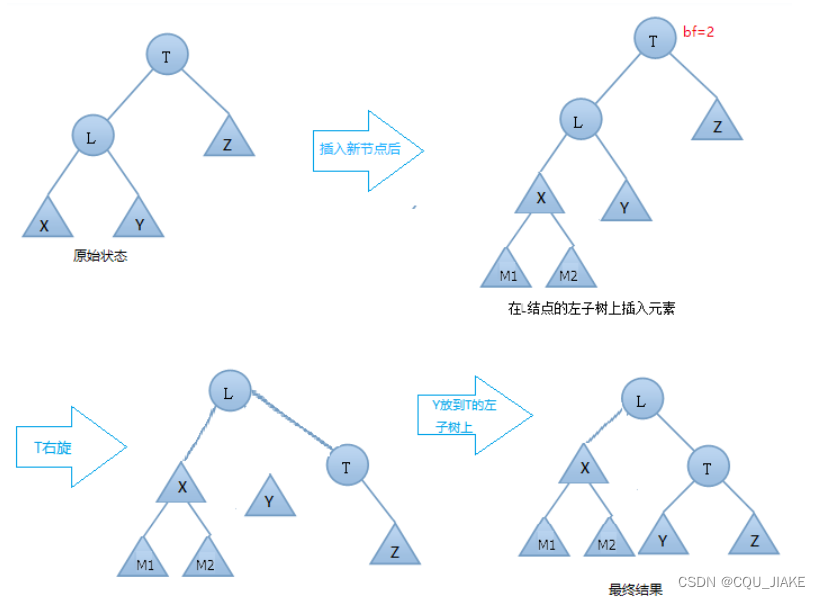
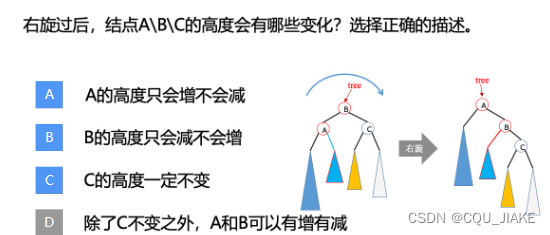
如何判断是否为AVL
AVL树高度

由于AVL树的左右子树都是AVL树,
自变量是N,AVL树的高度。那么由于AVL树左右平衡,根节点平衡,所以对于高度为d的AVL树,根节点占一层,那么左子树(默认左子树高一点)高度为d-1,(此时加起来为d);右子树高度为d-2,因为要满足左右子树高度差不大于1而且结点要尽可能少,所以有

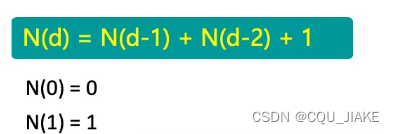
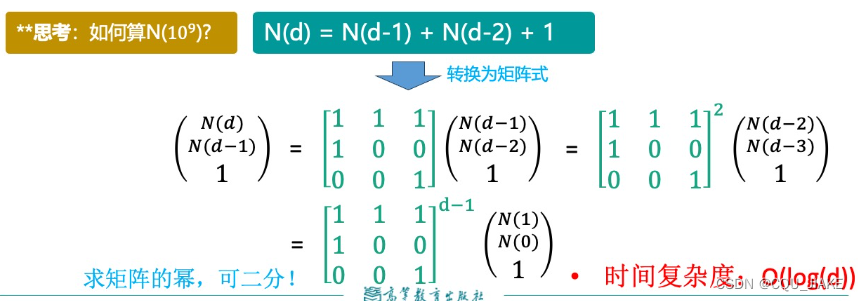
二分求矩阵的幂
快速幂
相关文章:

11.30BST理解,AVL树操作,定义;快速幂,二分求矩阵幂(未完)
完全二叉树结点的度可能有1,满二叉树的度只能为0或2 BST构建 BST是左孩子都比根节点小,右孩子都比根节点大 二叉搜索树的插入,删除,调整 平衡树理解 任何一个平衡二叉树,它的中序遍历都是一样的,都是有…...

深入理解Java核心技术:Java工程师的实用干货笔记
💂 个人网站:【 海拥】【神级代码资源网站】【办公神器】🤟 基于Web端打造的:👉轻量化工具创作平台💅 想寻找共同学习交流的小伙伴,请点击【全栈技术交流群】 在Java工程师的职业生涯中,深入理解…...

大学里面转专业介绍
目录 个人情况转专业过程中的经验分享转专业后的学习建议和心态调整转专业后的时间平衡 个人情况 信息科学与工程学院计算机科学与技术专业2019级本科生,曾从物理与微电子科学学院后转入信息科学与技术学院。学习成绩连续三年专业前10% 项目:爬虫项目、…...

MySQL_1. mysql数据库介绍
shell脚本差不多快完结了接下来会为大家更新MySQL系列的相关的基础知识笔记,希望对大家有所帮助,好废话不多说,接下来开始正题! 1.mysql数据库介绍 mysql 是一款安全、跨平台、高效的,并与 PHP、Java 等主流编程语言…...

TimeGPT:时间序列预测模型实例
时间序列预测领域正在经历一个非常激动人心的时期。在过去的三年里,我们见证了许多重要的贡献,如N-BEATS、N-HiTS、PatchTST和TimesNet等。同时,大型语言模型(LLM)近来在流行度方面取得了很大的成功,例如Ch…...

【JavaEE】多线程 (1)
目录 1. 认识线程(Thread) 1) 线程是什么 2) 为啥要有线程 3) 进程和线程的区别 2.第⼀个多线程程序 3.多线程的其他创建方式 方法二:实现 Runnable 接⼝ 方法三:匿名内部类 方法四:实现Runable, 重写run, 匿名内部类 方法五:使用lambda表达式…...

linux 应用层同步与互斥机制之条件变量
2、条件变量 互斥量防止多个线程同时访问同一共享变量。(我们称为互斥) 有一种情况,多个线程协同工作。一个线程的消费需要等待另一个线程的产出。必须线程B完成了应有的任务,满足了某一个条件,线程A才能继续执行。&…...

3.5毫米音频连接器接线方式
3.5毫米音频连接器接线方式 耳机插头麦克风插头 绘制电路图注意事项 3.5毫米音频连接器分为单声道开关型和无开关型如下图: sleeve(套筒) tip(尖端) ring(环) 耳机插头 麦克风插头 绘制电路图…...
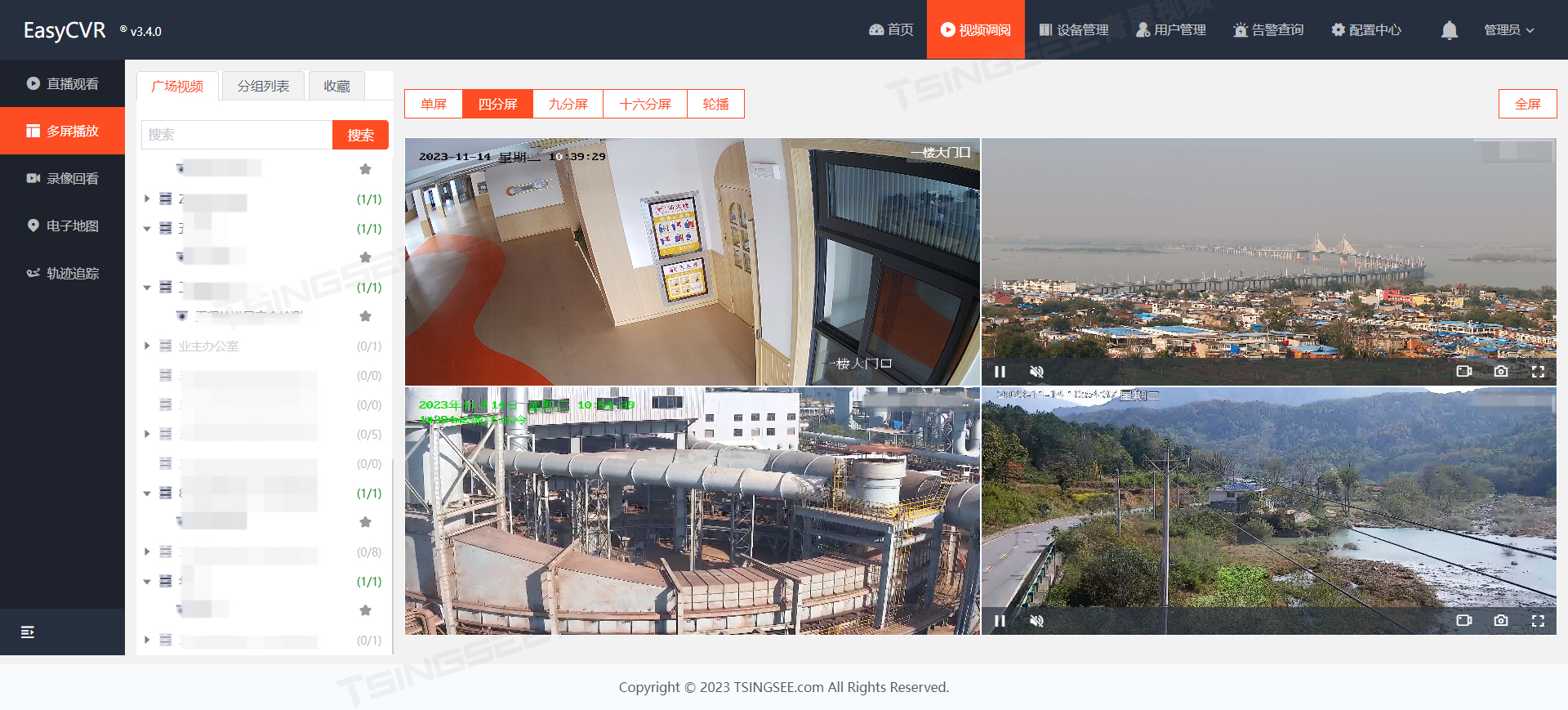
智慧农田可视化大数据综合管理平台方案,EasyCVR助力农业高质量发展
一、背景需求 我国是农业大国,农业耕地面积达到20亿亩。随着物联网、大数据、人工智能等新一代信息技术与农业农村加速融合,以及国家对农业的重视,智慧农业对于我国农业现代化建设和实施乡村振兴战略具有重大引领与推动作用。在传统农田生产…...
python超详细基础文件操作【建议收藏】
文章目录 前言1 文件操作1.1 文件打开与关闭1.1.1 打开文件1.1.2 关闭文件 1.2 访问模式及说明 2 文件读写2.1 写数据(write)2.2 读数据(read)2.3 读数据(readlines)2.3 读数据(readline&#x…...
华为变革进展指数TPM的五个级别:试点级、推行级、功能级、集成级和世界级
华为变革进展指数TPM的五个级别:试点级、推行级、功能级、集成级和世界级 TPM(Transformation Progress Metrics,变革进展指标)用来衡量管理体系在华为的推行程度和推行效果,并找出推行方面的不足与问题,…...

vue el-select多选封装及使用
使用了Element UI库中的el-select和el-option组件来构建多选下拉框。同时,也包含了一个el-input组件用于过滤搜索选择项,以及el-checkbox-group和el-checkbox组件用于显示多选项。 创建组件index.vue (src/common-ui/selectMultiple/index.vue) <tem…...
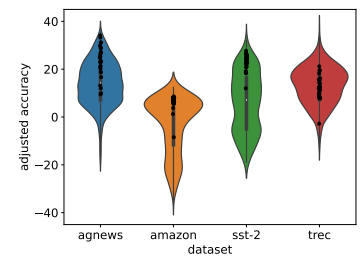
大模型上下文学习(ICL)训练和推理两个阶段31篇论文
大模型都火了这么久了,想必大家对LLM的上下文学习(In-Context Learning)能力都不陌生吧? 以防有的同学不太了解,今天我就来简单讲讲。 上下文学习(ICL)是一种依赖于大型语言模型的学习任务方式…...
zibll-7.5.1)
WordPress(安装比子主题文件)zibll-7.5.1
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、新建网站二、配置ssl三.配置伪静态四.上传文件五.添加本地访问前言 提示:这里可以添加本文要记录的大概内容: 首先,我们要先理解什么是授权原理。 原理就是我们大家运营网站,点击授权…...

蓝桥杯 动态规划
01 数字三角形 #include<bits/stdc.h> using namespace std; const int N105; using lllong long; ll a[N][N],dp[N][N]; int main(){int n;cin>>n;for(int i1;i<n;i){for(int j1;j<i;j){cin>>a[i][j];}}for(int i5;i>1;i--){for(int j1;j<i;j){…...
【图论】重庆大学图论与应用课程期末复习资料2-各章考点(计算部分)(私人复习资料)
图论各章考点 二、树1、避圈法(克鲁斯克尔算法)2、破圈法3、Prim算法 四、路径算法1、Dijkstra算法2、Floyd算法 五、匹配1、匈牙利算法(最大权理想匹配(最小权权值取反)) 六、行遍性问题1、Fleury算法&…...

整数和浮点数在内存中的存储(大小端详解)
目录 一、整数在内存中的存储 二、大小端字节序和字节序判断 2.1为什么有大小端? 2.2请简述大端字节序和小端字节序的概念,设计一个小程序来判断当前机器的字节序。(10分)-百度笔试题 方法一(char*强制类型转换)…...
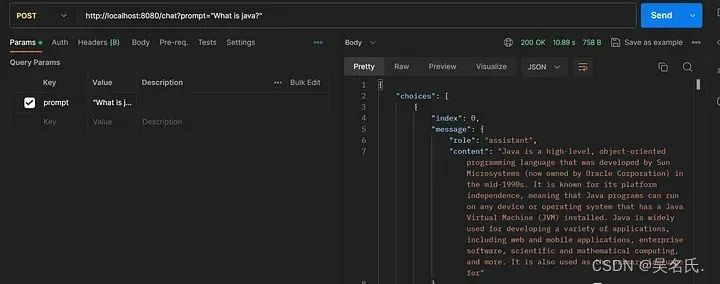
SpringBoot 集成 ChatGPT,实战附源码
1 前言 在本文中,我们将探索在 Spring Boot 应用程序中调用 OpenAI ChatGPT API 的过程。我们的目标是开发一个 Spring Boot 应用程序,能够利用 OpenAI ChatGPT API 生成对给定提示的响应。 您可能熟悉 ChatGPT 中的术语“提示”。在 ChatGPT 或类似语…...

数据结构——希尔排序(详解)
呀哈喽,我是结衣 不知不觉,我们的数据结构之路已经来到了,排序这个新的领域,虽然你会说我们还学过冒泡排序。但是冒泡排序的性能不高,今天我们要学习的希尔排序可就比冒泡快的多了。 希尔排序 希尔排序的前身是插入排…...
C++ day53 最长公共子序列 不相交的线 最大子序和
题目1:1143 最长公共子序列 题目链接:最长公共子序列 对题目的理解 返回两个字符串的最长公共子序列的长度,如果不存在公共子序列,返回0,注意返回的是最长公共子序列,与前一天的最后一道题不同的是子序…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

uniapp 开发ios, xcode 提交app store connect 和 testflight内测
uniapp 中配置 配置manifest 文档:manifest.json 应用配置 | uni-app官网 hbuilderx中本地打包 下载IOS最新SDK 开发环境 | uni小程序SDK hbulderx 版本号:4.66 对应的sdk版本 4.66 两者必须一致 本地打包的资源导入到SDK 导入资源 | uni小程序SDK …...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...
