最小二乘支持向量机”在学习偏微分方程 (PDE) 解方面的应用(Matlab代码实现)
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
👨💻4 Matlab代码
💥1 概述
本代码说明了“最小二乘支持向量机”在学习偏微分方程 (PDE) 解方面的应用。提供了一个示例,并将获得的结果与精确的解决方案进行比较。
📚2 运行结果
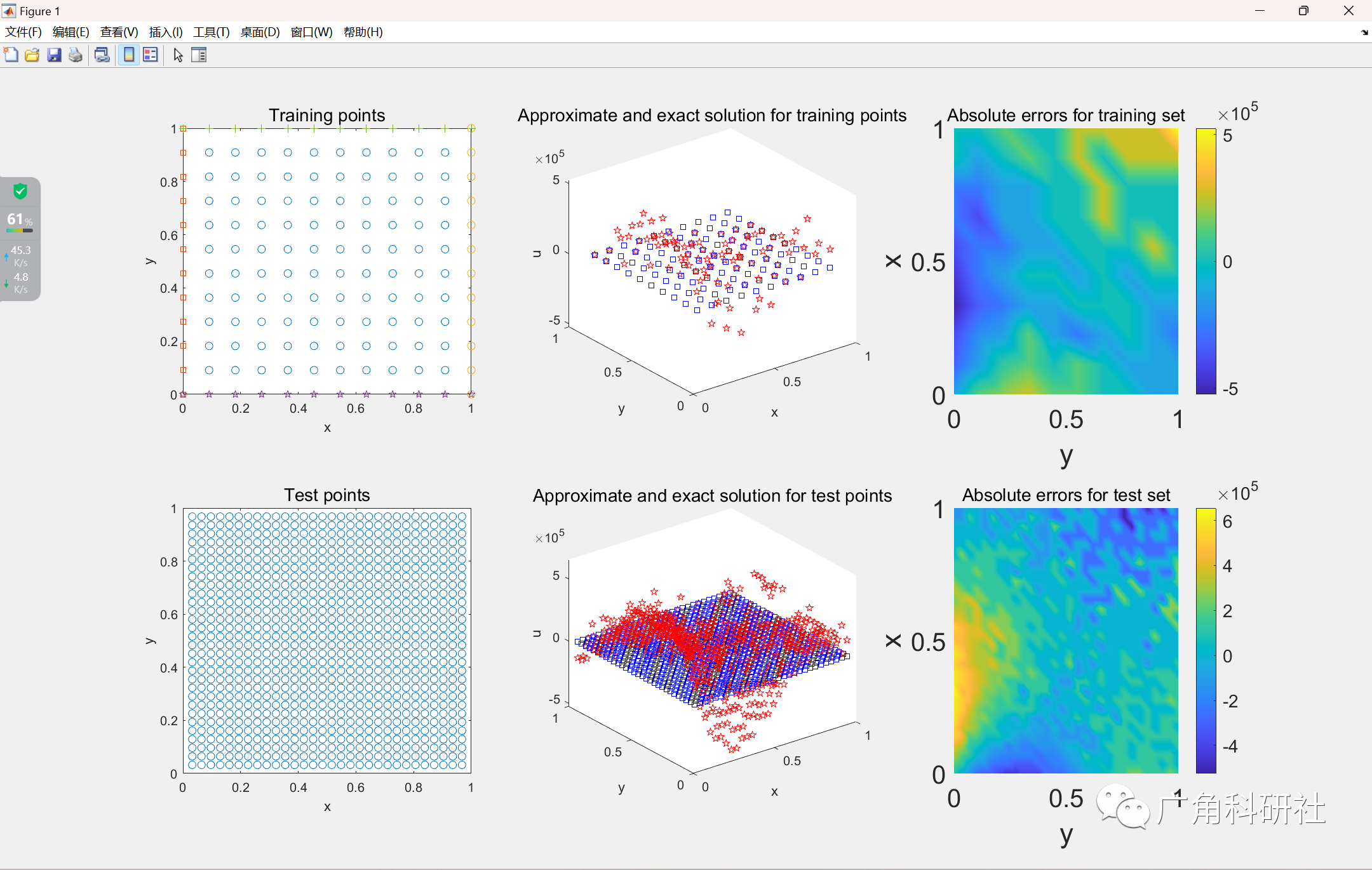
主函数部分代码:
clc; clear all; close all
warning('off','all')
a0=0;
b0=1;
n=11;
h=(b0-a0)/n;
[X1,Y1]=meshgrid(a0+h:h:b0-h);
W=[];
for i=1:size(X1,2)
Z=[X1(:,i),Y1(:,1)];
W=[W ; Z];
end
subplot(2,3,1)
plot(W(:,1),W(:,2),'o')
hold on
[X,Y]=meshgrid(a0:h:b0);
W2=[];
for i=1:size(X,2)
Z=[X(:,i),Y(:,1)];
W2=[W2 ; Z];
end
L1=[];
for i=1:n+1
L1=[L1 ; W2(i,:)];
end
L2=[];
for i=n*(n+1)+1:size(W2,1)
L2=[L2 ; W2(i,:)];
end
L3=[L1(:,2) L1(:,1)];
L4=[L2(:,2) L2(:,1)];
plot(L1(:,1),L1(:,2),'s')
plot(L2(:,1),L2(:,2),'o')
plot(L3(:,1),L3(:,2),'p')
plot(L4(:,1),L4(:,2),'+')
title('Training points','Fontsize',14)
xlabel('x')
ylabel('y')
%%
f=@(s,v) exp(-s).*(s-2+v.^3+6*v); % right hand side of the given PDE
gamma=10^14; % the regularization parameter
sig=0.95; % kernel bandwidth
K=KernelMatrix(W,'RBF_kernel',sig);
x=W(:,1);
y=W(:,2);
xx1=x*ones(1,size(x,1));
xx2=x*ones(1,size(x,1));
cof1=2*(xx1-xx2')/(sig);
xx3=y*ones(1,size(y,1));
xx4=y*ones(1,size(y,1));
cof2=2*(xx3-xx4')/(sig);
Kxx=(-2/sig)*K + (cof1.^2) .* K;
Kyy=(-2/sig)*K + (cof2.^2) .* K;
Kx2x2=( ( 12/(sig^2) - (12/sig)* (cof1.^2) + (cof1.^4) ) .*K);
Ky2y2=( ( 12/(sig^2) - (12/sig)* (cof2.^2) + (cof2.^4) ) .*K);
Kx2y2=( ( 4/(sig^2) - (2/sig)* (cof1.^2) - (2/sig)* (cof2.^2) + (cof1.^2).*(cof2.^2) ) .*K);
Ky2x2=( ( 4/(sig^2) - (2/sig)* (cof1.^2) - (2/sig)* (cof2.^2) + (cof1.^2).*(cof2.^2) ) .*K);
K1T= Kx2x2+ Kx2y2 + Ky2x2+ Ky2y2;
m=size(K1T,1);
%*******************************************************************
KL1=KernelMatrix(W,'RBF_kernel',sig,L1);
L1b1x=L1(:,1)*ones(1,size(x,1));
L1b2x=x*ones(1,size(L1(:,1),1));
cofL1x=-2*(L1b1x'-L1b2x)/(sig);
L1b1y=L1(:,2)*ones(1,size(y,1));
L1b2y=y*ones(1,size(L1(:,2),1));
cofL1y=-2*(L1b1y'-L1b2y)/(sig);
KL1xx=(-2/sig)*KL1 + (cofL1x.^2) .* KL1;
KL1yy=(-2/sig)*KL1 + (cofL1y.^2) .* KL1;
KL1T= KL1xx+ KL1yy;
%*************************************************
KL2=KernelMatrix(W,'RBF_kernel',sig,L2);
L2b1x=L2(:,1)*ones(1,size(x,1));
L2b2x=x*ones(1,size(L2(:,1),1));
cofL2x=-2*(L2b1x'-L2b2x)/(sig);
L2b1y=L2(:,2)*ones(1,size(y,1));
L2b2y=y*ones(1,size(L2(:,2),1));
cofL2y=-2*(L2b1y'-L2b2y)/(sig);
KL2xx=(-2/sig)*KL2 + (cofL2x.^2) .* KL2;
KL2yy=(-2/sig)*KL2 + (cofL2y.^2) .* KL2;
KL2T= KL2xx+ KL2yy;
%*************************************************
KL3=KernelMatrix(W,'RBF_kernel',sig,L3);
L3b1x=L3(:,1)*ones(1,size(x,1));
L3b2x=x*ones(1,size(L3(:,1),1));
cofL3x=-2*(L3b1x'-L3b2x)/(sig);
L3b1y=L3(:,2)*ones(1,size(y,1));
L3b2y=y*ones(1,size(L3(:,2),1));
cofL3y=-2*(L3b1y'-L3b2y)/(sig);
KL3xx=(-2/sig)*KL3 + (cofL3x.^2) .* KL3;
KL3yy=(-2/sig)*KL3 + (cofL3y.^2) .* KL3;
KL3T= KL3xx+ KL3yy;
%*************************************************
KL4=KernelMatrix(W,'RBF_kernel',sig,L4);
L4b1x=L4(:,1)*ones(1,size(x,1));
L4b2x=x*ones(1,size(L4(:,1),1));
cofL4x=-2*(L4b1x'-L4b2x)/(sig);
L4b1y=L4(:,2)*ones(1,size(y,1));
L4b2y=y*ones(1,size(L4(:,2),1));
cofL4y=-2*(L4b1y'-L4b2y)/(sig);
KL4xx=(-2/sig)*KL4 + (cofL4x.^2) .* KL4;
KL4yy=(-2/sig)*KL4 + (cofL4y.^2) .* KL4;
KL4T= KL4xx+ KL4yy;
%*************************************************
KL1L1=KernelMatrix(L1,'RBF_kernel',sig,L1);
KL2L1=KernelMatrix(L2,'RBF_kernel',sig,L1);
KL3L1=KernelMatrix(L3,'RBF_kernel',sig,L1);
KL4L1=KernelMatrix(L4,'RBF_kernel',sig,L1);
%*************************************************
KL1L2=KernelMatrix(L1,'RBF_kernel',sig,L2);
KL2L2=KernelMatrix(L2,'RBF_kernel',sig,L2);
KL3L2=KernelMatrix(L3,'RBF_kernel',sig,L2);
KL4L2=KernelMatrix(L4,'RBF_kernel',sig,L2);
%************************************************
KL1L3=KernelMatrix(L1,'RBF_kernel',sig,L3);
KL2L3=KernelMatrix(L2,'RBF_kernel',sig,L3);
KL3L3=KernelMatrix(L3,'RBF_kernel',sig,L3);
KL4L3=KernelMatrix(L4,'RBF_kernel',sig,L3);
%************************************************
KL1L4=KernelMatrix(L1,'RBF_kernel',sig,L4);
KL2L4=KernelMatrix(L2,'RBF_kernel',sig,L4);
KL3L4=KernelMatrix(L3,'RBF_kernel',sig,L4);
KL4L4=KernelMatrix(L4,'RBF_kernel',sig,L4);
%************************************************
A= [K1T+1/gamma*eye(m) , KL1T , KL2T, KL3T , KL4T , zeros((n-1)^2,1) ;....
KL1T' , KL1L1' , KL2L1' , KL3L1' , KL4L1' , ones(n+1,1) ;...
KL2T' , KL1L2' , KL2L2' , KL3L2' , KL4L2' , ones(n+1,1) ;...
KL3T' , KL1L3' , KL2L3' , KL3L3' , KL4L3' , ones(n+1,1) ;...
KL4T' , KL1L4' , KL2L4' , KL3L4' , KL4L4' , ones(n+1,1) ;...
zeros((n-1)^2,1)' , ones(n+1,1)' , ones(n+1,1)' , ones(n+1,1)' , ones(n+1,1)' , 0 ];
B=[f(W(:,1),W(:,2)); L1(:,2).^3 ; (1+L2(:,2).^3)*exp(-1) ; L3(:,1).*exp(-L3(:,1)) ; exp(-L4(:,1)).*(L4(:,1)+1) ; 0 ];
result=A\B;
alpha=result(1:m);
beta1=result(m+1:m+n+1);
beta2=result(m+n+2:m+2*n+2);
beta3=result(m+2*n+3:m+3*n+3);
beta4=result(m+3*n+4:m+4*n+4);
b=result(end);
%% Result for training points
yhat= (Kxx' + Kyy')* alpha + KL1 * beta1 + KL2* beta2 + KL3* beta3 + KL4* beta4 +b;
yexa=@(p,q) exp(-p).*(p+q.^3);
yexact=yexa(W(:,1),W(:,2));
Error1= yexact- yhat;
MAX_Absolute_error_training=max(abs(yhat-yexact));
RMSE_training=sqrt(mse(yhat-yexact));
fprintf('------- training set ------------------\n\n')
fprintf('Max Abs Error on training set=%d\n',MAX_Absolute_error_training)
fprintf('RMSE on training set=%d\n\n',RMSE_training)
subplot(2,3,2)
plot3(W(:,1),W(:,2),yhat,'pr')
hold all
plot3(W(:,1),W(:,2),yexact,'sb')
title('Approximate and exact solution for training points','Fontsize',14)
xlabel('x')
ylabel('y')
zlabel('u')
NError=reshape(Error1,size(X1,1),size(Y1,1));
Xn=linspace(0,1,n-1);
Yn=linspace(0,1,n-1);
subplot(2,3,3)
surface(Xn,Yn,NError)
shading interp
xlabel('y','Fontsize',14)
ylabel('x','Fontsize',14)
set(gca,'Fontsize',20)
grid on
h=colorbar;
set(h,'fontsize',14);
title('Absolute errors for training set','Fontsize',14)
%% Result for test points
a0=0;
b0=1;
n=31;
h=(b0-a0)/n;
[X2,Y2]=meshgrid(a0+h:h:b0-h);
WT=[];
for i=1:size(X2,2)
Z=[X2(:,i),Y2(:,1)];
WT=[WT ; Z];
end
subplot(2,3,4)
plot(WT(:,1),WT(:,2),'o')
title('Test points','Fontsize',14)
xlabel('x')
ylabel('y')
Kt=KernelMatrix(W,'RBF_kernel',sig,WT);
xt=WT(:,1);
yt=WT(:,2);
xx1t=x*ones(1,size(xt,1));
xx2t=xt*ones(1,size(x,1));
cof1t=-2*(xx1t-xx2t')/(sig);
xx3t=y*ones(1,size(yt,1));
xx4t=yt*ones(1,size(y,1));
cof2t=-2*(xx3t-xx4t')/(sig);
Ktestxx=(-2/sig)*Kt + (cof1t.^2) .* Kt;
Ktestyy=(-2/sig)*Kt + (cof2t.^2) .* Kt;
KKlte1=KernelMatrix(WT,'RBF_kernel',sig,L1);
KKlte2=KernelMatrix(WT,'RBF_kernel',sig,L2);
KKlte3=KernelMatrix(WT,'RBF_kernel',sig,L3);
KKlte4=KernelMatrix(WT,'RBF_kernel',sig,L4);
Ytest= (Ktestxx' + Ktestyy')* alpha + KKlte1 * beta1 + KKlte2* beta2 + KKlte3* beta3 + KKlte4* beta4 + b;
yextest=yexa(WT(:,1),WT(:,2));
subplot(2,3,5)
plot3(WT(:,1),WT(:,2),Ytest,'pr')
hold on
plot3(WT(:,1),WT(:,2),yextest,'sb')
title('Approximate and exact solution for test points','Fontsize',14)
xlabel('x')
ylabel('y')
zlabel('u')
yextest=yexa(WT(:,1),WT(:,2));
MAX_Absolute_error_test=max(abs(Ytest-yextest));
RMSE_test=sqrt(mse(Ytest-yextest));
fprintf('------- test set ------------------\n\n')
fprintf('Max Abs Error on test set=%d\n',MAX_Absolute_error_test)
fprintf('RMSE on test set=%d\n\n',RMSE_test)
fprintf('------- Finished -----------------------\n\n')
Error= Ytest - yextest ;
Ytnew=reshape(Ytest,size(X2,1),size(Y2,1));
Ytexa=reshape(yextest,size(X2,1),size(Y2,1));
NError=reshape(Error,size(X2,1),size(Y2,1));
Xn=linspace(0,1,n-1);
Yn=linspace(0,1,n-1);
subplot(2,3,6)
surface(Xn,Yn,NError)
shading interp
xlabel('y','Fontsize',14)
ylabel('x','Fontsize',14)
set(gca,'Fontsize',20)
grid on
h=colorbar;
set(h,'fontsize',14);
title('Absolute errors for test set','Fontsize',14)
🎉3 参考文献
[1] Mehrkanoon S., Falck T., Suykens J.A.K., "Approximate Solutions to Ordinary Differential Equations Using Least Squares Support Vector Machines",IEEE Transactions on Neural Networks and Learning Systems, vol. 23, no. 9, Sep. 2012, pp. 1356-1367.
[2] Mehrkanoon S., Suykens J.A.K.,"LS-SVM approximate solution to linear time varying descriptor systems", Automatica, vol. 48, no. 10, Oct. 2012, pp. 2502-2511.
[3] Mehrkanoon S., Suykens J.A.K., "Learning Solutions to Partial Differential Equations using LS-SVM",Neurocomputing, vol. 159, Mar. 2015, pp. 105-116.
👨💻4 Matlab代码
相关文章:

最小二乘支持向量机”在学习偏微分方程 (PDE) 解方面的应用(Matlab代码实现)
目录 💥1 概述 📚2 运行结果 🎉3 参考文献 👨💻4 Matlab代码 💥1 概述 本代码说明了“最小二乘支持向量机”在学习偏微分方程 (PDE) 解方面的应用。提供了一个示例,…...
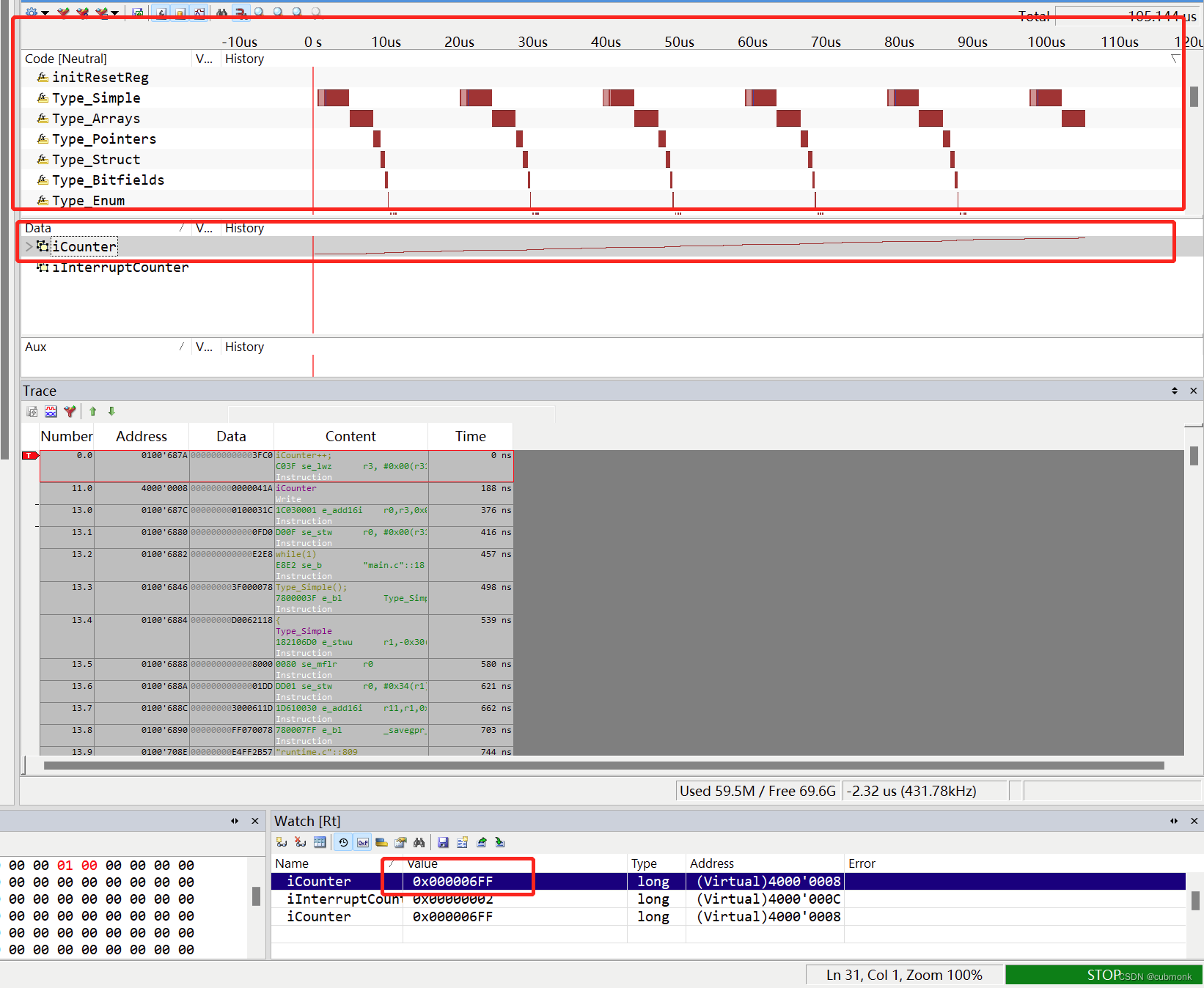
ISYSTEM调试实践8-winIDEA Analyzer功能1
前面几篇介绍了ISYSTEM的基本调试界面和功能,相比我之前用过的IDE,除了几种断点方式和脚本功能以外,应该都是比较简单,稍微操作一下就可以直接上手,后续我将介绍winIDEA的Analyzer 功能。 1 Analyzer简介 iSYSTEM An…...
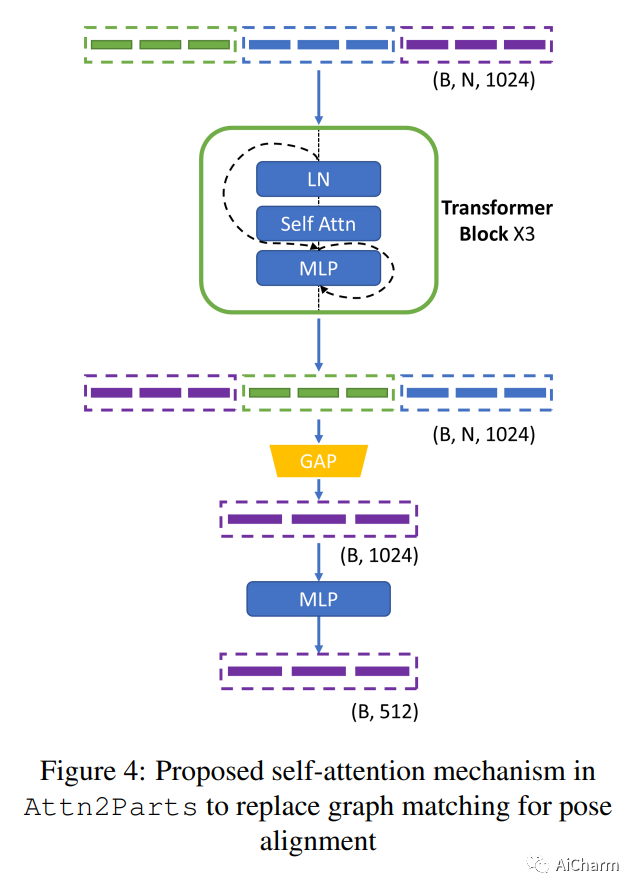
每日学术速递2.11
CV - 计算机视觉 | ML - 机器学习 | RL - 强化学习 | NLP 自然语言处理 Subjects: cs.IR、cs.MM 1.A Comprehensive Survey on Multimodal Recommender Systems: Taxonomy, Evaluation, and Future Directions 标题:关于多模态推荐系统的综合调查:分…...
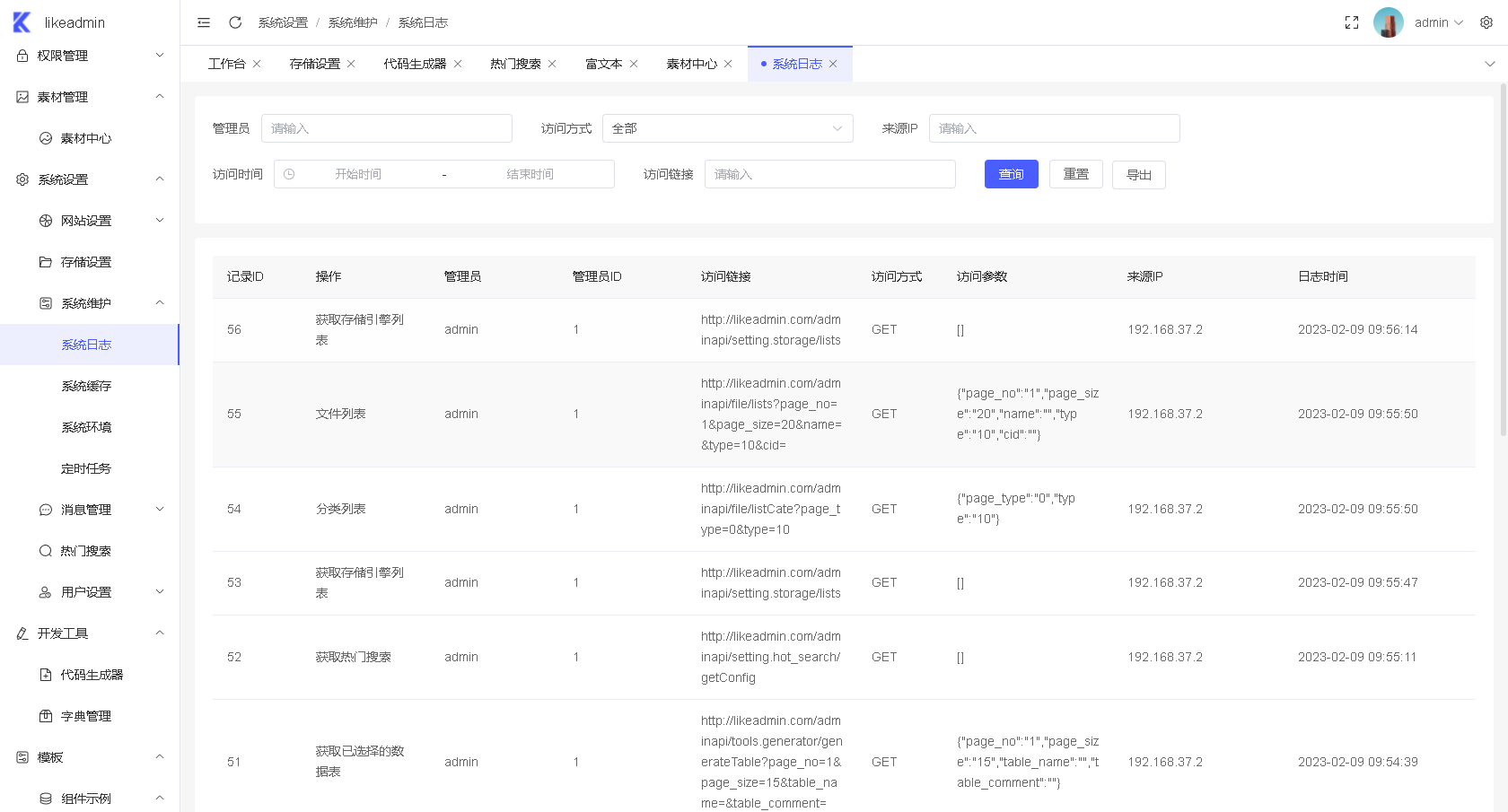
宝塔搭建实战php开源likeadmin通用管理admin端vue3源码(二)
大家好啊,我是测评君,欢迎来到web测评。 上一期给大家分享了server端的部署方式,今天来给大家分享admin端在本地搭建,与打包发布到宝塔的方法。感兴趣的朋友可以自行下载学习。 技术架构 vscode node16 vue3 elementPlus vit…...
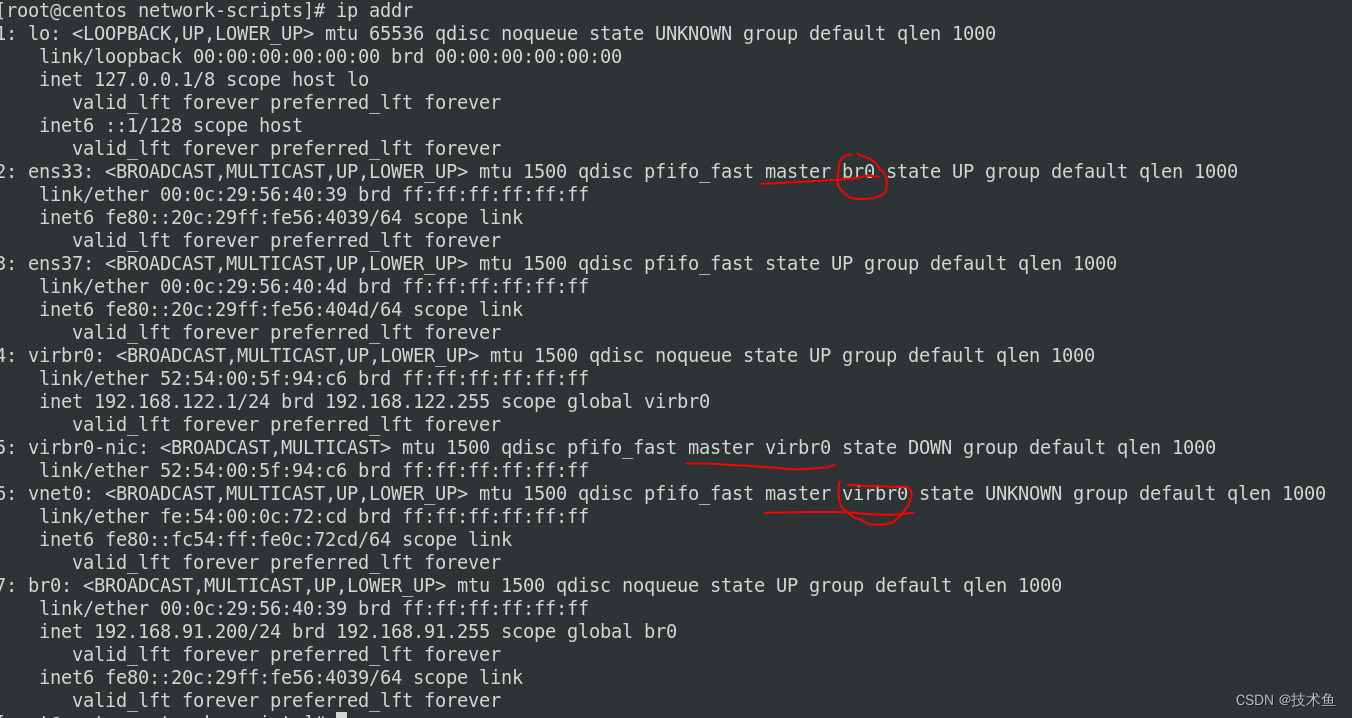
网络基础-虚拟化工具-网桥
系列文章目录 本系列文章主要是回顾和学习工作中常用的网络基础命令,在此记录以便于回顾。 该篇文章主要是讲解虚拟化的工具网桥相关的概念和常用命令 提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录系…...

剑指 Offer 14- II. 剪绳子 II
剑指 Offer 14- II. 剪绳子 II 给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]…k[m - 1] 。请问 k[0]k[1]…*k[m - 1] 可能的最大乘积是多少&a…...

English Learning - Day55 作业打卡 2023.2.9 周四
English Learning - Day55 作业打卡 2023.2.9 周四引言1. Jim 在看电视的时候他的老婆正在做饭。2. 他刚睡着电话就响了。3. 我正在想事情,这时忽然有人从后面抓我胳膊。4. 我们总是边吃火锅边唱歌。5. 他一听说出了事故,马上就来了现场。6. He entered …...
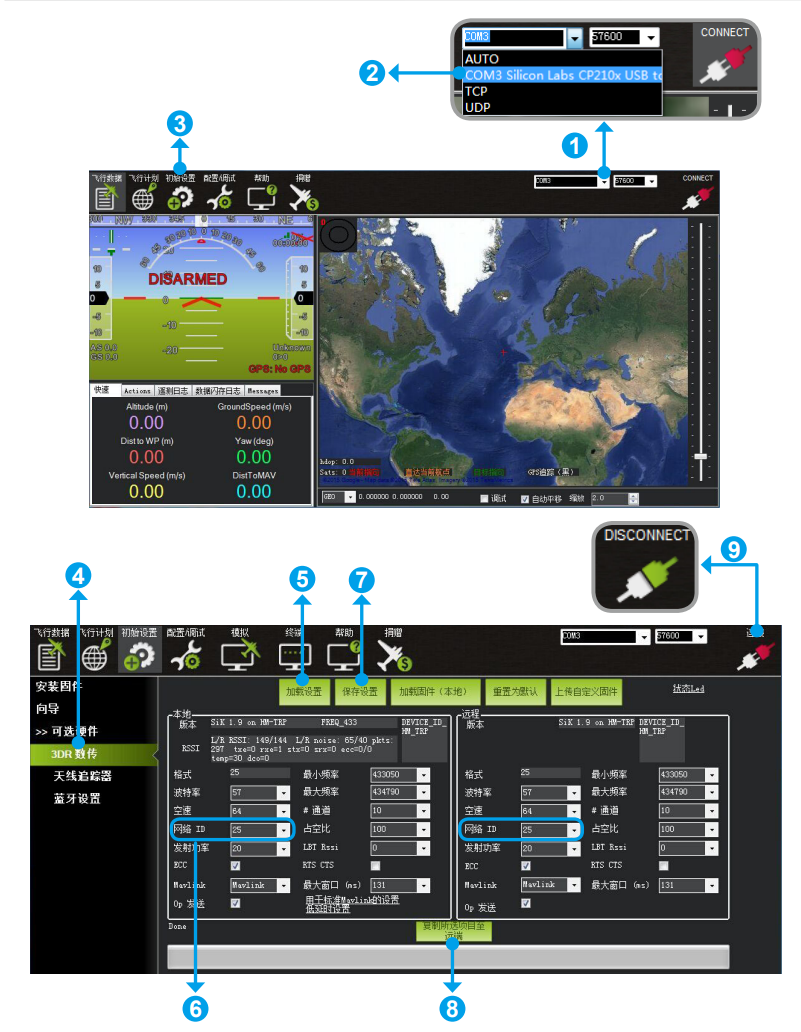
pixhawk2.4.8-地面站配置-APM固件
文章目录一、硬件准备二、软件准备1 已实飞测试2 MP地面站 任意版本下载:3 APM固件 任意版本下载:三、飞控校准1 刷固件2 机架选择3 加速度计校准4 指南针校准5 遥控器校准6 飞行模式7 紧急断电&无头模式8 基础参数设置9 电流计校准10 电调校准11 起…...

golang 通道类型
文章目录一、什么是通道类型二、通道产生的原因三、声明channel四、创建channel五、channel相关操作1、发送值2、接收值3、关闭通道3.1 注意3.2 特点四、通道类型1、无缓冲通道2、有缓冲通道五、单向通道一、什么是通道类型 Go 语言中的通道(channel)是一…...

并发、并行、吞吐量、延迟、响应时间 含义理解
并发、并行、吞吐量、延迟、响应时间 知识点了解 1. 响应时间(RT) 理解:响应时间是指系统对请求作出响应的时间。例如一个正在运行的服务,服务内程序接受到参数请求开始,到程序计算完,并将结果返回出去结束,这段时间…...
HTTP 和 HTTPS 的区别
文章目录前言一、HTTP 与 HTTPS 的基本概念HTTPHTTPS二、HTTP 和 HTTPS协议的区别前言 浏览网站时,我们会发现网址有两种格式,一种以http://开头,一种https://开头。好像这两种格式差别不大,只多了一个s,实际上他们有…...
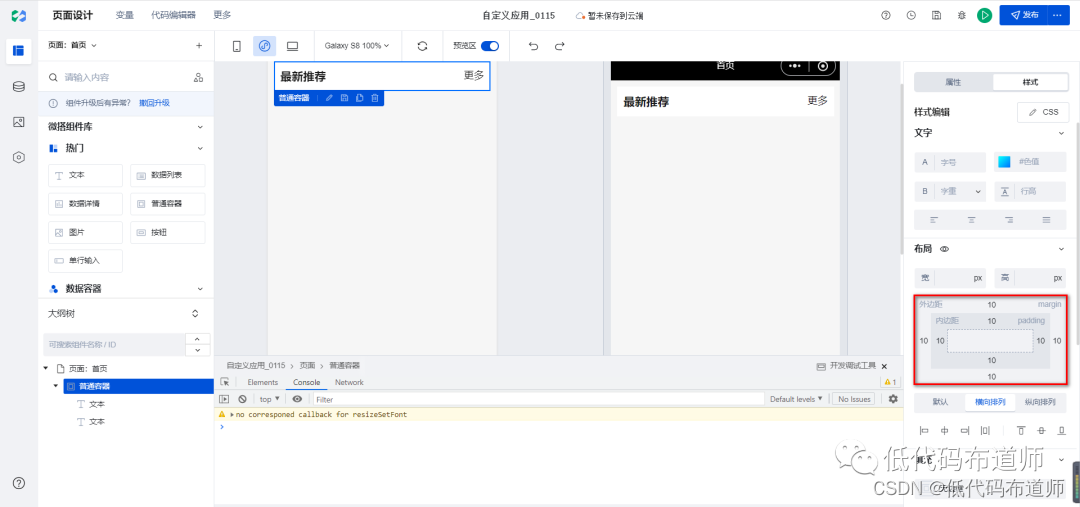
微搭低代码从入门到精通07-基础布局组件
低码开发不同于传统开发,传统开发我们通常需要编写前端代码和后端代码。前端代码由HTML、CSS和JavaScript组成,后端代码我们通常要用后端语言比如Java来编写接口。 低码开发的特点是可视化开发,在编辑器中通过组件的拖拽来完成页面的编制。如…...
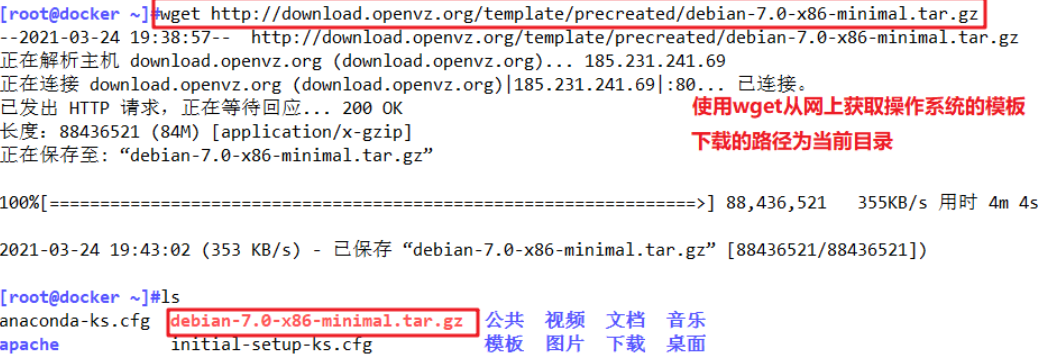
Docker镜像的创建
Docker镜像Docker镜像Docker 镜像是一个特殊的文件系统提供容器运行时所需的程序、库、资源、配置等文件包含一些为运行时准备的一些配置参数(如匿名卷、环境变量、用户等)镜像不包含任何动态数据,其内容在构建之后也不会被改变。Docker镜像的…...
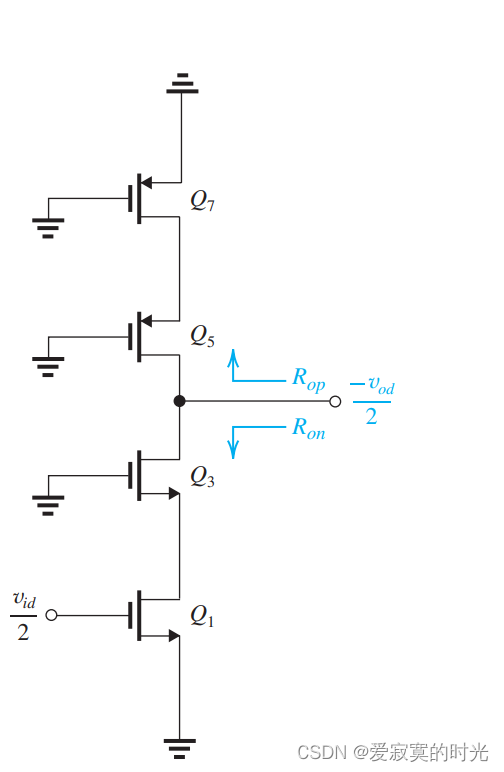
电子技术——MOS差分输入对
电子技术——MOS差分输入对 差分输入系统因其极高的共模抑制能力,差分输入几乎是是构建所有通用模拟IC的基本前级输入,也是现代信号传输理论的基础。本节我们讲解MOS差分输入对。 MOS差分输入对 下图展示了MOS差分输入对的基本原理图: 一个…...

树莓派 - 小记
文章目录关于树莓派Raspberry Pi OSGPIOScratch 编程Minecraft相关硬件关于树莓派 树莓派:Raspberry Pi,由美国树莓派基金会开发,是一款专门用于计算机教育的极简计算机。 第一代发布于 2012年。 特点:精致小巧,价格低…...
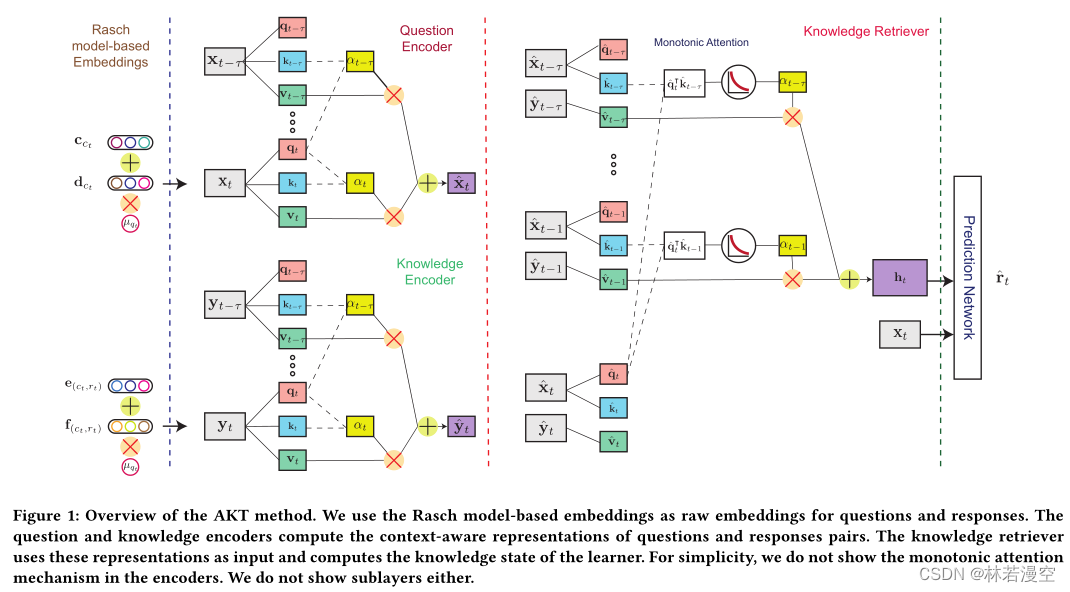
【论文解读|KDD2020】AKT. Context-Aware Attentive Knowledge Tracing
文章目录摘要1 引言1.1 贡献3 模型3.4 基于Rasch模型的嵌入5 结论摘要 知识追踪(KT)是指根据学习者在教育应用中的过去表现预测未来学习者表现的问题。KT最近使用灵活的基于深度神经网络的模型的发展在这一任务中表现出色。然而,这些模型通常提供有限的可解释性&am…...

Geek Uninstaller:向流氓软件火力全开,超良心的软件彻底卸载工具
写在前面 我们在电脑上安装软件,以及在使用软件的过程中,会产生一些程序文件、注册表项和临时文件等,用来支持软件的正常使用,都是正常现象。 但是,在卸载软件时,很多软件自身的卸载程序很不负责任&#…...

Java线程池
什么是线程池 线程池是指在初始化一个多线程应用程序过程中创建一个线程集合,然后在需要执行新的任务时重用这些线程而不是新建一个线程。线程池中线程的数量通常完全取决于可用内存数量和应用程序的需求。然而,增加可用线程数量是可能的。线程池中的每…...
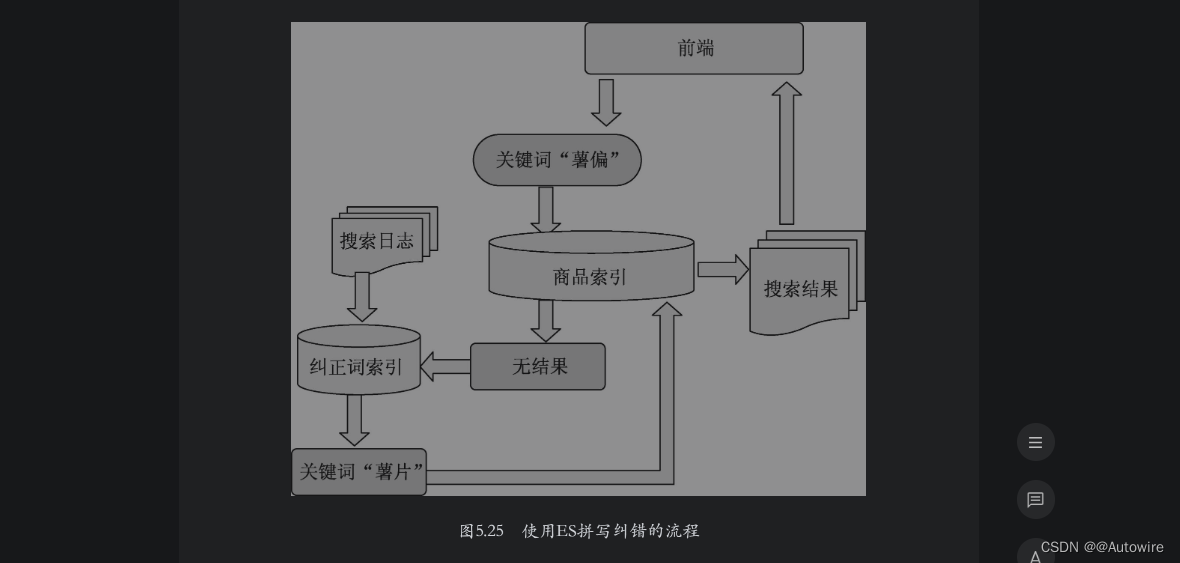
2023-02-10 - 5 文本搜索
与其他需要精确匹配的数据不同,文本数据在前期的索引构建和搜索环节都需要进行额外的处理,并且在匹配环节还要进行相关性分数计算。本章将详细介绍文本搜索的相关知识。 本章首先从总体上介绍文本的索引建立过程和搜索过程,然后介绍分析器的…...
,简单直白)
华为OD机试 - 最近的医院(Python),简单直白
任务混部 | 华为 OD 机试【最新】 题目 新型冠状病毒疫情的肆虐,使得家在武汉的大壮不得不思考自己家和附近定点医院的具体情况。 经过一番调查, 大壮明白了距离自己家最近的定点医院有两家。其中医院 A 距离自己的距离是 X 公里,医院 B 距离自己的距离是 Y 公里。 由于…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...
