简介Kadane算法及相关的普通动态规划
简介Kadane算法及相关的普通动态规划
本文详细论述Kadane算法的经典题目,并通过“首先列出动态规划解法,再改为Kadane算法解法”的方式,讲解二者的不同。最后给出一道Kadane算法变体的题目,解法极为简洁优美。
Kadane算法也是一种动态规划算法,它的时间复杂度也是O(n), 但它与普通的动态规划有什么不同呢?这里先给出结论,不同就是:它的空间复杂度是O(1),而普通动态规划的空间复杂度是O(n).
下面的例题-1是一道经典的可以用Kadane算法求解的题目。
例题-1 LeetCode-53
给定一个整数数组,求它的子数组之和的最大值。
比如,数组为[-2,1,-3,4,-1,2,1,-5,4], 则子数组元素之和最大为6,因为当子数组为 [4,-1,2,1]时可取得最大值。
解法-1. 普通动态规划法
众所周知,动态规划法需要有一个递推公式。这个公式的思考与解析如下。
假设有一个同样大小的dp数组,其第i个位置的元素dp[i]的含义是:原整数数组s从0至i处且包含元素i时的所有子数组中子数组元素之和的最大值。
听见来很拗口是不是。说白了就是,对于所有的以s[i]为最右元素的子数组求子数组元素之和,最大的那个值就是dp[i].
想一想,如果我们知道了所有的dp[0], dp[1], …,dp[size-1], 那么我们是不是就知道了子数组之和的最大值了呢。
这里要注意的是,当 i < j < size 时, dp[i] 有可能大于 dp[j].
知道 dp[i] 的定义后,那么 dp[i+1] 是什么呢?
很明显,dp[i] 与 dp[i+1] 的差异就在于原数组的第 i+1 个元素,即 s[i+1].
一种可能是:s[i+1]可以被继续累加到当前最大值上,即dp[i]和s[i+1]都是非负数,那么 dp[i+1] = dp[i] + s[i+1]
另一种可能是:s[i+1]不可以被继续累加到当前最大值上, 比如:dp[i]是负数,而s[i+1]又比dp[i]大, 于是只好从s[i+1]开始算,即 dp[i+1] = s[i+1]
综合这2个式子:dp[i+1] = max(dp[i]+s[i+1], s[i+1])
换一种写法: dp[i] = max(dp[i-1]+s[i], s[i])
在当前定义下,我们最后需要返回 dp 数组中的最大元素。
这里有一个问题,为什么不能把 dp[i] 定义为“从0至i处的所有子数组中子数组元素之和的最大值”呢?
如果可以这么定义的话,那么我们就不需要在dp数组中找一个最大值,而只要返回dp数组的最后一个元素即可了。
其实对于有些问题时完全可以这么做的,比如下面的例题-2.
但是对于例题-1来说,鉴于其所求是子数组元素之和的最大值,它相当于对之前的多个元素有依赖关系,如果那样定义的话,则无法建立dp[i+1]和dp[i]之间的递推关系。
这个问题是一个隐藏较深且不太容易解释的问题。喜欢对算法作深入思考的朋友可以多想想这里,看是否有更加简洁精辟的见解。
普通动态规划法的代码还是比较简洁的,如下:
class Solution {public int maxSubArray(int[] nums) {int [] dp = new int [nums.length];dp[0] = nums[0];int result = nums[0];for (int i=1; i<nums.length; i++) {dp[i] = Math.max(nums[i], nums[i]+dp[i-1]);result = Math.max(result, dp[i]);}return result;}
}
解法-2. Kadane算法
上面的整个dp数组是否必要呢?
其实不是必要的。公式中的 dp[i] 和 dp[i-1] 看似不同,但其实可以巧妙地用一个变量来代表,从而整个dp数组也就不需要了 – 只用一个变量来维护dp[i]. 所以Kadane算法的空间复杂度是O(1). 这个技巧还是很值得学习的。
代码如下:
class Solution {public int maxSubArray(int[] nums) {int max_here = nums[0];int result = nums[0];for (int i=1; i<nums.length; i++) {max_here = Math.max(nums[i], nums[i]+max_here);result = Math.max(result, max_here);}return result;}
}
例题-1中对于dp[i]的定义还是不那么符合人的直觉的,而下面例题-2对 dp[i] 的设定则非常直接了。
例题-2. LeetCode-121
给定一个整数数组,其中每一个数字代表了股票在当天的价格。你每天只能操作一次,这一次是买或者卖股票,请最大化利润。
比如:[7,1,5,3,6,4],最大化利润是5. 因为在价格为1的那天买,在价格为6的那天卖,可以得到5的利润。
解法-1. 普通动态规划法
有了前面那么难的题,这题就简单了。对于动态规划,就是主要要考虑递推公式。
设定一个同样大小的数组dp,那么很自然地就想到 dp[i] 就代表到当天为止的最大利润。
那么dp[i+1]是什么呢? 假设原数组叫prices, 此时相当于多了一个 prices[i+1], 所引起的变化就是也许 prices[i+1] 能得到更高利润。
怎么会得到更高利润呢?如果用prices[i+1]减去之前的最小值,则是它得到的利润值;如果这个值比dp[i]大,则有了更高利润。
由此可见,要记录一个历史最小值。这个并不难实现。
这样一分析,递推公式就出来了: dp[i+1] = max(dp[i], prices[i+1]-minValue)
由此也可见,我们最后需要返回的就是 dp[size-1],即dp数组的最后一个元素。
普通动态规划法代码如下:
int maxProfit(vector<int>& prices) {if (prices.empty()) return 0;vector<int> dp(prices.size());dp[0] = 0;int minPrice = prices[0];for (int i=1; i<prices.size(); i++) {dp[i] = max(dp[i-1], prices[i] - minPrice);if (prices[i] < minPrice) minPrice = prices[i];}return dp[prices.size()-1];
}
解法-2. Kadane算法
仍然对普通动态规划法稍作优化,用一个变量代替dp[i]和dp[i+1], 由此消除dp数组。
代码如下:
int maxProfit(vector<int>& prices) {if (prices.empty()) return 0;int max_here = 0;int minPrice = prices[0];for (int i=1; i<prices.size(); i++) {max_here = max(max_here, prices[i] - minPrice);if (prices[i] < minPrice) minPrice = prices[i];}return max_here;
}
除了上面2道例题,有的时候会出现 Kadane 算法的变体。这个时候需要因为一些特殊条件而做出一些巧妙的变化,则可以继续使用Kadane算法。
例题-3 LeetCode-152
给定一个整数数组,求其子数组的乘积最大值。
比如:[2,3,-2,4],其子数组乘积最大值为6,因为 2x3=6.
首先,还是要找出递推数组。假设dp[i]为“至位置i处的包含了位置i的子数组乘积最大值”,那么对于例子中给定的数组,对应的dp数组是这样的:[2, 6, -2, 4]
所以, dp[i+1] = max(dp[i]*s[i+1], s[i])
由此似乎可以写出程序了。和例题-1很像嘛!是不是直接套就可以了?
但注意这样的数组: [-2, 3, -4], 很明显答案是24,但应用上面算法的dp数组是 [-2, 3, 3].
原因很简单,每遇到负数一次则结果反转,也就是说,如果应用了上面的算法,则-2无法被后面再一次遇到负数时用上。
换句话说,尽管dp[1]为3是正确的,但dp[2]还是3就不正确了,而此时dp[0]或原数组nums[0]的信息无法被dp[2]用上。
至此,普通的动态规划似乎不再能够应用了,因为递推关系似乎无法推出来。怎么办呢?其实Kadane算法仍可以应用。
鉴于负数每乘一次都会反转结果,我们就只好一直乘,直至结尾。如果负数的个数是偶数,则这就是结果(先不考虑0)。
但如果负数的个数是奇数,比如1个,那我们就不知道是在这个负数的左边还是右边会出现乘积最大值了。
这又怎么办呢?也很好办。从左往右和从右往左分别扫一遍。因为我们不可能在一遇到负数的时候就重启计算。
最后,一旦遇到0怎么办呢?这就要重启计算了。相当于数字0将数组分段了。一旦遇到0,则从0后面的第1个数字开始,重启我们的乘法运算,直至下一个0或数组在当前方向上结束。
啰里吧嗦说了很多,但代码其实还是很简洁的。
class Solution {public int maxProduct(int[] nums) {long r1 = Integer.MIN_VALUE;long p1 = 1;for (int i=0; i<nums.length; i++) {p1 = p1 * nums[i];if (p1 > r1) r1 = p1;if (p1 == 0) p1 = 1;}long r2 = Integer.MIN_VALUE;long p2 = 1;for (int i=nums.length-1; i>=0; i--) {p2 = p2 * nums[i];if (p2 > r2) r2 = p2;if (p2 == 0) p2 = 1;}return (int)(r1>r2?r1:r2);}
}
由本题可见,Kadane算法其实可能比普通动态规划更加灵活。
(END)
相关文章:

简介Kadane算法及相关的普通动态规划
简介Kadane算法及相关的普通动态规划 本文详细论述Kadane算法的经典题目,并通过“首先列出动态规划解法,再改为Kadane算法解法”的方式,讲解二者的不同。最后给出一道Kadane算法变体的题目,解法极为简洁优美。 Kadane算法也是一…...
校园教务管理系统
学年论文(课程设计) 题目: 信息管理系统 校园教务管理系统 摘要:数据库技术是现代信息科学与技术的重要组成部分,是计算机数据处理与信息管理系统的核心,随着计算机技术的发展,数据库技…...

【LeetCode热题100】【双指针】接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。 示例 1: 输入:height [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] …...
)
软件工程-(可行性分析、需求分析)
目录 一.可行性研究 1.1定义 1.2项目背景 1.3三方面研究目标系统的可行性 1.3.1技术可行性分析 1.3.2 经济可行性分析 1.3.3 市场可行性分析 1.4. 数据流图 数据字典(DD) 1.5风险评估 1.6结论与建议 二、需求分析 引言 项目概述 利益相关者分析…...
HuggingFace学习笔记--BitFit高效微调
1--BitFit高效微调 BitFit,全称是 bias-term fine-tuning,其高效微调只去微调带有 bias 的参数,其余参数全部固定; 2--实例代码 from datasets import load_from_disk from transformers import AutoTokenizer, AutoModelForCaus…...

阅读笔记|A Survey of Large Language Models
阅读笔记 模型选择:是否一定要选择参数量巨大的模型?如果需要更好的泛化能力,用于处理非单一的任务,例如对话,则可用选更大的模型;而对于单一明确的任务,则不一定越大越好,参数小一…...
JSP 设置静态文件资源访问路径
这里 我们先在 WEB目录webapp 下创建一个包 叫 static 就用它来存静态资源 然后 我们扔一张图片进去 我们直接这样写 如下图 找到父级目录 然后寻找下面的 static 下的 img.png 运行代码 很明显 它没有找到 这边 我们直接找到 webapp目录下的 WEB-INF目录下的 web.xml 加入…...

【Pytorch】Visualization of Feature Maps(4)——Saliency Maps
学习参考来自 Saliency Maps的原理与简单实现(使用Pytorch实现)https://github.com/wmn7/ML_Practice/tree/master/2019_07_08/Saliency%20Maps Saliency Maps 原理 《Deep Inside Convolutional Networks: Visualising Image Classification Models and Saliency Maps》&…...
java第三十课
电商项目(前台): 登录接口 注册接口后台: 注册审核:建一个线程类 注意程序中的一个问题。 这里是 5 条记录,2 条记录显示应该是 3 页,实际操作过程 有审核机制,出现了数据记录动态变…...

Scala--2
package scala02object Scala07_typeCast {def main(args: Array[String]): Unit {// TODO 隐式转换// 自动转换val b: Byte 10var i: Int b 10val l: Long b 10 100Lval fl: Float b 10 100L 10.5fval d: Double b 10 100L 10.5f 20.00println(d.getClass…...
【SQL SERVER】定时任务
oracle是定时JOB,sqlserver是创建作业,通过sqlserver代理实现 先看SQL SERVER代理得服务有没有开 选择计算机右键——>管理——>服务与应用程序——>服务——>SQL server 代理 然后把SQL server 代理(MSSQLSERVER)启…...

MyBatis-Plus学习笔记(无脑cv即可)
1.MyBatis-Plus 1.1特性 无侵入:只做增强不做改变,引入它不会对现有工程产生影响,如丝般顺滑损耗小:启动即会自动注入基本 CURD,性能基本无损耗,直接面向对象操作强大的 CRUD 操作:内置通用 M…...

【VUE】watch 监听失效
如果你遇见了这个问题,那么尝试在 watch 函数中设置 { deep: true } 选项。这告诉 Vue 监听对象或数组内部的变化,就像下面这样: watch(()>chatStore.dataSources,(oldValue, newValue)>{// 监听执行逻辑 }, { deep: true })嗯&#x…...
python的异常处理批量执行网络设备的巡检命令
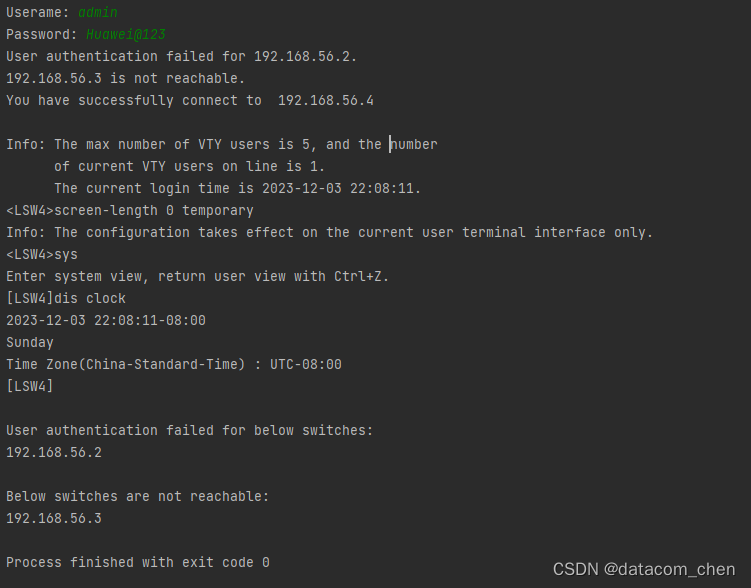
前言 在网络设备数量超过千台甚至上万台的大型企业网中,难免会遇到某些设备的管理IP地址不通,SSH连接失败的情况,设备数量越多,这种情况发生的概率越高。 这个时候如果你想用python批量配置所有的设备,就一定要注意这…...
react native 环境准备
一、必备安装 1、安装node 注意 Node 的版本应大于等于 16,安装完 Node 后建议设置 npm 镜像(淘宝源)以加速后面的过程(或使用科学上网工具)。 node下载地址:Download | Node.js设置淘宝源 npm config s…...
PGSQL(PostgreSQL)数据库安装教程
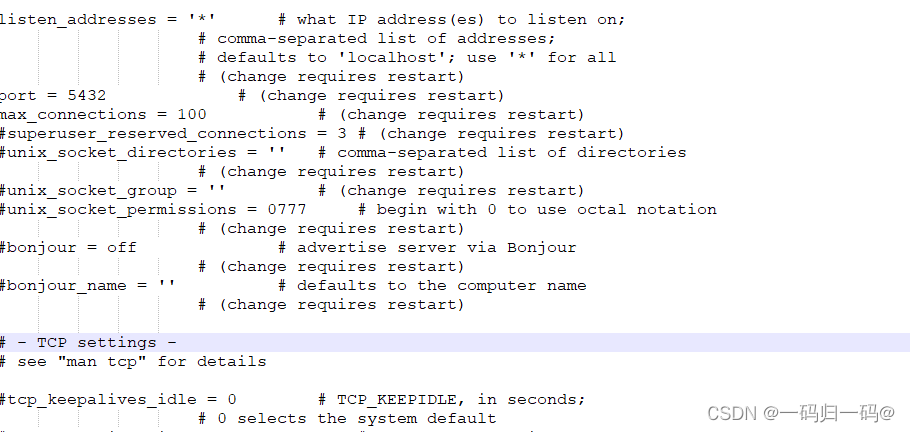
安装包下载 下载地址 下载后点击exe安装包 设置的data存储路径 设置密码 设置端口 安装完毕,配置PGSQL的ip远程连接,pg_hba.conf,postgresql.conf,需要更改这两个文件 pg_hba.conf 最后增加一行 host all all …...

识别和修复网站上损坏链接的最佳实践
如果您有一个网站,我们知道您花了很多时间在它上面,以使其成为最好的资源。如果你的链接不起作用,你的努力可能是徒劳的。您网站上的断开链接可能会以两种方式损害您的业务: 它们对企业来说是可怕的,因为当消费者点击…...

使用Navicat连接MySQL出现的一些错误
目录 一、错误一:防火墙未关闭 二、错误二:安全组问题 三、错误三:MySQL密码的加密方式 四、错误四:修改my.cnf配置文件 一、错误一:防火墙未关闭 #查看防火墙状态 firewall-cmd --state#关闭防…...
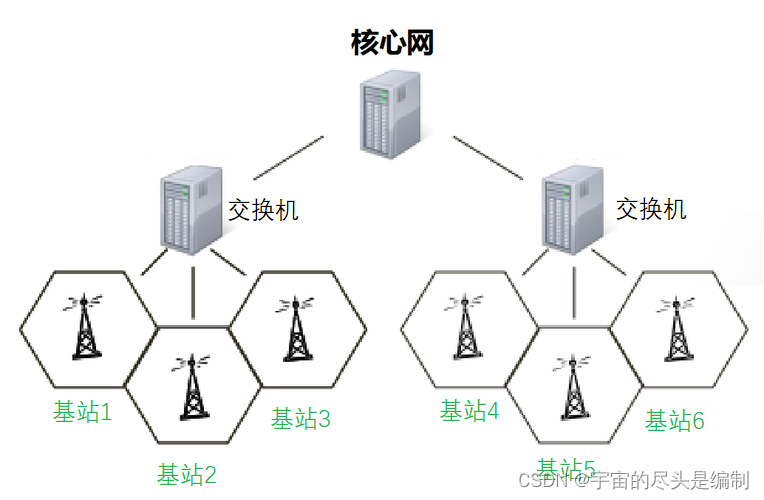
4G基站BBU、RRU、核心网设备
目录 前言 基站 核心网 信号传输 前言 移动运营商在建设4G基站的时候,除了建设一座铁塔之外,更重要的是建设搭载铁塔之上的移动通信设备,这篇博客主要介绍BBU,RRU以及机房的核心网等设备。 基站 一个基站有BBU,…...
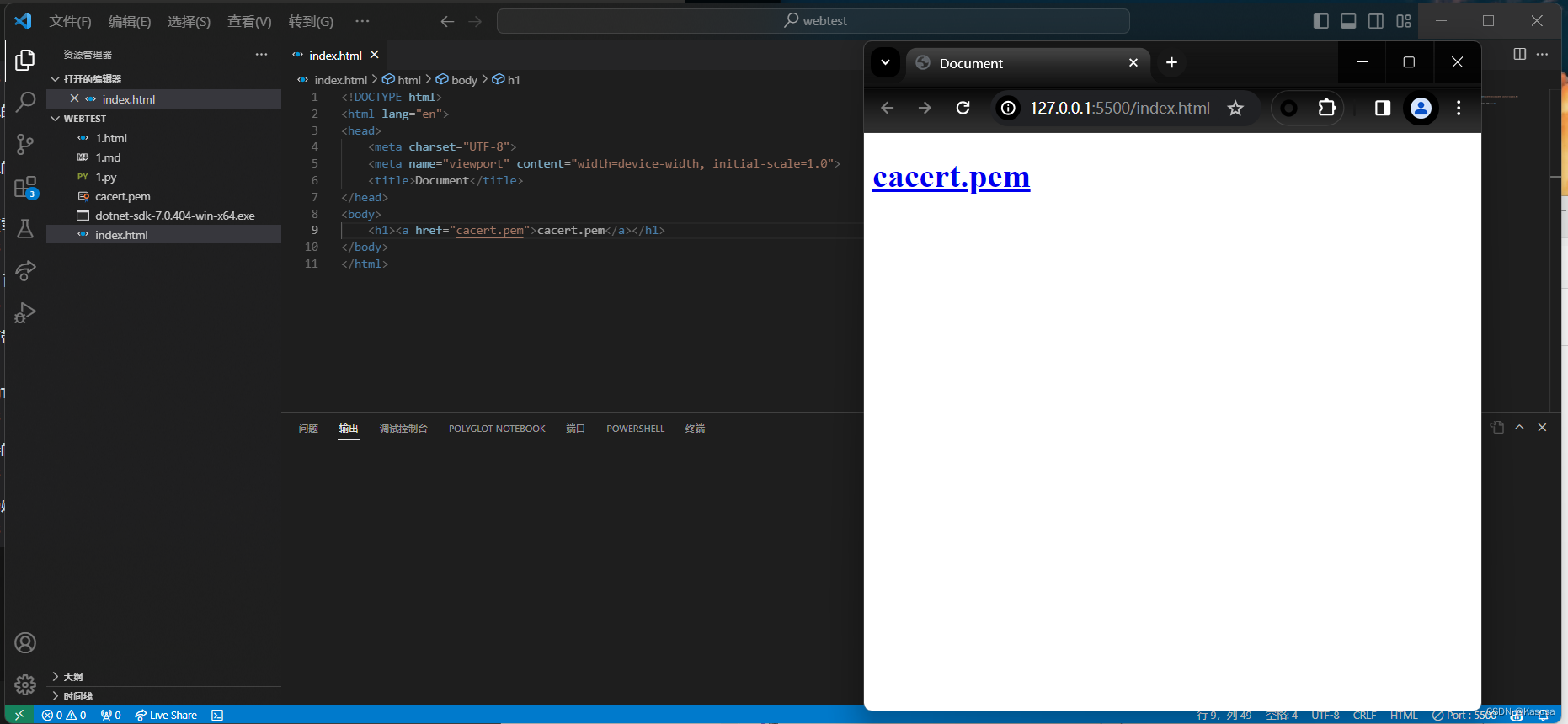
iphone/安卓手机如何使用burp抓包
iphone 1. 电脑 ipconfig /all 获取电脑网卡ip: 192.168.31.10 2. 电脑burp上面打开设置,proxy,增加一条 192.168.31.10:8080 3. 4. 手机进入设置 -> Wi-Fi -> 找到HTTP代理选项,选择手动,192.168.31.10:8080 …...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

汽车生产虚拟实训中的技能提升与生产优化
在制造业蓬勃发展的大背景下,虚拟教学实训宛如一颗璀璨的新星,正发挥着不可或缺且日益凸显的关键作用,源源不断地为企业的稳健前行与创新发展注入磅礴强大的动力。就以汽车制造企业这一极具代表性的行业主体为例,汽车生产线上各类…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...

基于单片机的宠物屋智能系统设计与实现(论文+源码)
本设计基于单片机的宠物屋智能系统核心是实现对宠物生活环境及状态的智能管理。系统以单片机为中枢,连接红外测温传感器,可实时精准捕捉宠物体温变化,以便及时发现健康异常;水位检测传感器时刻监测饮用水余量,防止宠物…...

跨平台商品数据接口的标准化与规范化发展路径:淘宝京东拼多多的最新实践
在电商行业蓬勃发展的当下,多平台运营已成为众多商家的必然选择。然而,不同电商平台在商品数据接口方面存在差异,导致商家在跨平台运营时面临诸多挑战,如数据对接困难、运营效率低下、用户体验不一致等。跨平台商品数据接口的标准…...

js 设置3秒后执行
如何在JavaScript中延迟3秒执行操作 在JavaScript中,要设置一个操作在指定延迟后(例如3秒)执行,可以使用 setTimeout 函数。setTimeout 是JavaScript的核心计时器方法,它接受两个参数: 要执行的函数&…...
