【数据结构】—红黑树(C++实现)

🎬慕斯主页:修仙—别有洞天
💜本文前置知识: AVL树
♈️今日夜电波:Letter Song—ヲタみん
1:36━━━━━━️💟──────── 5:35
🔄 ◀️ ⏸ ▶️ ☰
💗关注👍点赞🙌收藏您的每一次鼓励都是对我莫大的支持😍
目录
一、前言
红黑树的概念
红黑树与二叉搜索树的异同
二、红黑树的实现
节点的定义
AVL树的初始化定义
红黑树的插入(重点及难点!!!)
插入大致步骤
插入的总体逻辑
按照二叉搜索树的方法插入节点
父节点为红色, 需要进行相应的调整
情况一: cur为红,p为红,g为黑,u存在且为红
情况二: cur为红,p为红,g为黑,u不存在/u存在且为黑编辑
情况三: cur为红,p为红,g为黑,u不存在/u存在且为黑
插入实现
根据构建红黑树的规则验证红黑树
求红黑树高度以及遍历红黑树
三、总体代码
一、前言
本文是基于二叉搜索树以及AVL树的知识前提下对于红黑树进行叙述的,主要叙述的方面同AVL树一样,主要是在于插入方面的解析,其它部分同AVL树和二叉搜索树还是有些相似的。但是对于删除部分来说,红黑树就太难了,举个例子?:插入部分,红黑树的实现大概180行代码,而删除则是400往上接近500行了。难度可想而知,作者如果有能力后续会慢慢补齐的!
红黑树的概念
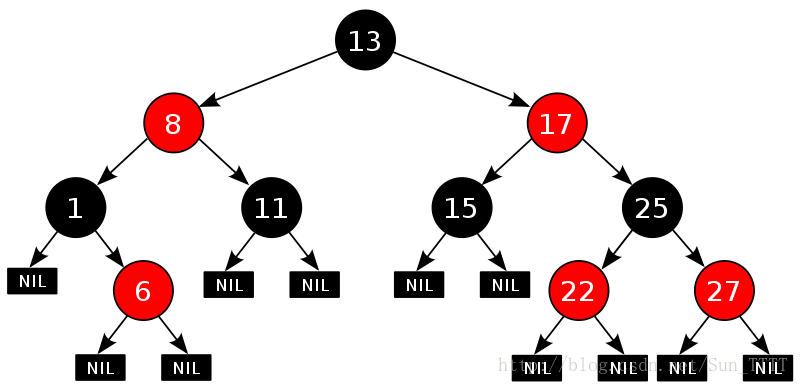
红黑树是一种自平衡二叉查找树,它的每个节点都有一个颜色属性,可以是红色或黑色。红黑树的特性如下:
- 每个节点要么是红色,要么是黑色。
- 根节点是黑色。
- 所有的叶子节点(NIL节点)都是黑色。(注意NIL实际上空节点,只不过我们将所有空节点看作黑色节点而已)
- 如果一个节点是红色,那么它的两个子节点都是黑色。(意味着黑色可以有黑色的节点也可以有红色的节点,但是红色只能有黑色的节点)
- 对于每个节点,从该节点到其所有后代叶节点的简单路径上,均包含相同数目的黑色节点。
这些特性保证了红黑树的搜索效率。在最坏的情况下,搜索一棵高度为h的红黑树的时间复杂度是O(h),与AVL树相当。此外,由于红黑树的插入和删除操作不需要像AVL树那样频繁地旋转,因此红黑树在实际应用中比AVL树更加稳定和高效。
在实际应用中,红黑树常用于实现关联数组(哈希表)的数据结构,以及数据库索引等场合。
红黑树与二叉搜索树的异同
红黑树和二叉搜索树的主要区别在于它们如何处理数据冲突。
二叉搜索树(BST)是一种特殊的二叉树,其中每个节点都存储一个键值,并且满足左子树中的所有键值小于根节点的键值,右子树中的所有键值大于根节点的键值。这使得搜索、插入和删除操作可以在平均情况下以O(log n)的时间复杂度完成。
红黑树也是一种二叉搜索树,但它通过限制每个节点的颜色和位置关系来保持树的平衡,从而确保搜索、插入和删除操作的时间复杂度始终为O(log n)。与BST不同的是,红黑树还具有以下特点:
* 每个节点要么是红色,要么是黑色。
* 根节点是黑色。
* 所有的叶子节点(NIL节点,空节点)都是黑色。
* 如果一个节点是红色,那么它的两个子节点都是黑色。
* 对于每个节点,从该节点到其所有后代叶节点的简单路径上,均包含相同数目的黑色节点。这些特性使得红黑树在实际应用中更加强大和灵活。例如,红黑树可以通过左右旋转变换快速调整树的形状,从而应对动态数据集的变化。此外,红黑树还可以应用于许多不同的场景,如数据库索引、排序算法、集合类数据结构等等。
二、红黑树的实现
节点的定义
使用枚举来定义结点的颜色,提高代码的可读性。定义三叉链,方便后续的旋转等等操作,定义KV结构的红黑树,定义一个枚举变量用于储存颜色。通过构造函数初始化节点。
enum Color
{RED,BLACK
};template<class K, class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Color _col;RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED){}
};
AVL树的初始化定义
template<class K, class V>
struct RBTree
{typedef RBTreeNode<K, V> Node;public:bool Insert(const pair<K, V>& kv)//插入操作bool IsBalance();//判断是否符合红黑树int Height();//求高度private:Node* _root = nullptr;//给缺省初始化};红黑树的插入(重点及难点!!!)
插入大致步骤
下面是红黑树插入的大致步骤:
1. 向红黑树中插入新的节点。
2. 确保新节点的颜色为红色。
3. 确保新插入的节点不会破坏红黑树的性质。如果新节点违反了某些性质,则需要对红黑树进行旋转操作或更改节点的颜色。
4. 返回到插入节点的父节点,继续执行第3步,直到所有违反性质的节点都被修复为止。
具体来说,当我们向红黑树中插入新的节点时,我们需要遵循以下规则:
- 每个节点都是红色或黑色。
- 根节点是黑色。
- 所有叶子节点(NIL节点,空节点)都是黑色。
- 如果一个节点是红色,则它的两个子节点都是黑色。
- 对于每个节点,从该节点到其所有后代叶子节点的简单路径上,均包含相同数目的黑色节点。
如果我们违反了这些规则中的任何一个,我们就可以通过旋转操作或更改节点的颜色来修复这个问题。例如,如果我们发现某个节点有两个子节点都是红色的,那么我们就需要将这个节点以及其两个子节点的颜色全部改为黑色,然后再将该节点的父节点变为红色。这样就可以确保新插入的节点不会破坏红黑树的性质。
插入的总体逻辑
- 按二叉搜索树的插入方法,找到待插入位置。
- 将待插入结点插入到树中。(新插入的节点默认为红)
- 若插入结点的父结点是红色的,则需要对红黑树进行调整。
- 按情况进行调整:情况一: cur为红,p为红,g为黑,u存在且为红。->将p,u改为黑,g改为红,然后把g当成cur,继续向上调整。情况二: cur为红,p为红,g为黑,u不存在/u存在且为黑->p为g的左孩子,cur为p的左孩子,则进行右单旋转;相反, p为g的右孩子,cur为p的右孩子,则进行左单旋转p、g变色--p变黑,g变红。情况三: cur为红,p为红,g为黑,u不存在/u存在且为黑->p为g的左孩子,cur为p的右孩子,则针对p做左单旋转,再对g做右单旋;相反, p为g的右孩子,cur为p的左孩子,则针对p做右单旋转,再对g做左单旋。
按照二叉搜索树的方法插入节点
按照搜索二叉树,大往右,小往左的思想,找到对应的节点,插入节点并且链接。大致步骤都是同二叉搜索树是相同的,只不过需要注意的是新插入的节点默认都是红色的。当父节点为黑色时,直接插入即可。
bool Insert(const pair<K, V>& kv)
{if (_root == nullptr)//如果根节点为空则直接开辟一个节点作为根节点并且返回true{_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;//后续遍历找位置以及旋转等Node* cur = _root;//遍历用while (cur) // 开始遍历到指定位置->其实就是到cur为空节点的地方{if (cur->_kv.first < kv.first)//要插入节点大于则往右遍历{parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first)//要插入节点小于于则往左遍历{parent = cur;cur = cur->_left;}else{return false;}}//默认新增节点给红色,防止给黑破坏平衡cur = new Node(kv);cur->_col = RED;if (parent->_kv.first < kv.first)//同父节点比大小{parent->_right = cur;//链接新节点}else{parent->_left = cur;//链接新节点}cur->_parent = parent;//新节点链接父节点//后续根据红黑树特性开始调整...//调整完毕}_root->_col = BLACK;//将根处理成黑。因为插入向上处理会改变,但是当最后为根时改变后就不能进入循环,因此需要最后处理为黑return true;
}父节点为红色, 需要进行相应的调整
重点在于看舅舅节点,看舅舅节点的存在与否,存在的话是红色?还是黑色? 根据舅舅节点来确定相应的调整操作。然后再看新插入节点cur处于parent的位置,在左?还是在右?进行相应的调整策略。
情况一: cur为红,p为红,g为黑,u存在且为红

当cur为红,p为红,g为黑,u存在且为红时,将p,u改为黑,g改为红,然后把g当成cur,继续向上调整。
情况二: cur为红,p为红,g为黑,u不存在/u存在且为黑

当cur为红,p为红,g为黑,u不存在/u存在且为黑,u不存在,如果p为g的左,cur为p的左,如上图一所示,则只需对g进行右单旋,如果p为g的右,cur为p的右,则只需对g进行左单旋,然后p、g变色--p变黑,g变红。
当u存在且为黑,即如上图二第2步所示。由图二1、2步我们可以知道cur是由于新增节点而变化而来的,我们也可以根据红黑树的定义可知,c、d、e分别为对应箭头的颜色。由此,我们需要进行对应的旋转以及变色操作,对于以上u存在且为黑,如果p为g的左,cur为p的左,则如图二第3步所示,对p进行右单旋,如果p为g的右,cur为p的右,则只需对g进行左单旋,然后p、g变色--p变黑,g变红。
情况三: cur为红,p为红,g为黑,u不存在/u存在且为黑


当cur为红,p为红,g为黑,u不存在/u存在且为黑,但是此时,如果p为g的左,cur为p的右,则如图所示需先对p进行左单旋,再对g进行右单旋。如果p为g的右,cur为p的左,则需对p进行右单旋,再对g进行左单旋。然后c、g变色--c变黑,g变红。
插入实现
bool Insert(const pair<K, V>& kv){if (_root == nullptr)//如果根节点为空则直接开辟一个节点作为根节点并且返回true{_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;//后续遍历找位置以及旋转等Node* cur = _root;//遍历用while (cur) // 开始遍历到指定位置->其实就是到cur为空节点的地方{if (cur->_kv.first < kv.first)//要插入节点大于则往右遍历{parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first)//要插入节点小于于则往左遍历{parent = cur;cur = cur->_left;}else{return false;}}//默认新增节点给红色,防止给黑破坏平衡cur = new Node(kv);cur->_col = RED;if (parent->_kv.first < kv.first)//同父节点比大小{parent->_right = cur;//链接新节点}else{parent->_left = cur;//链接新节点}cur->_parent = parent;//新节点链接父节点//根据红黑树特性开始调整while (parent && parent->_col == RED)//由于子节点和父节点都是红色,则需要调整{Node* grandfather = parent->_parent;//储存爷爷节点,用于找舅舅节点以及变色甚至旋转if (parent == grandfather->_left){// g// p u// cNode* uncle = grandfather->_right;//如果父亲节点在爷爷的左则舅舅在右if (uncle && uncle->_col == RED)//情况一:“变色处理” 舅舅节点存在且为红色,则我们需要将父亲以及舅舅变黑,爷爷变红{// 变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续向上处理cur = grandfather;parent = cur->_parent;}else //情况二:“需要旋转(单旋?or双旋?)+变色处理” 即舅舅节点存在时为黑或者舅舅节点不存在,则我们需要进行相应的旋转{if (cur == parent->_left){// 单旋// g p // p -> c g// cRotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// 双旋// g g p // p -> c -> c g// c pRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else // parent == grandfather->_right{// g// u p // c//Node* uncle = grandfather->_left;//情况一,但是uncle在左// u存在且为红if (uncle && uncle->_col == RED){// 变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续向上处理cur = grandfather;parent = cur->_parent;}else//情况二:“需要旋转(单旋?or双旋?)+变色处理”{if (cur == parent->_right){// 单旋// g p // p -> g c// cRotateL(grandfather);grandfather->_col = RED;parent->_col = BLACK;}else{// g g c// u p -> u c -> g p// c p u//RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;//将根处理成黑。因为插入向上处理会改变,但是当最后为根时改变后就不能进入循环,因此需要最后处理为黑return true;}void RotateL(Node* parent){++_rotateCount;Node* cur = parent->_right;Node* curleft = cur->_left;parent->_right = curleft;if (curleft){curleft->_parent = parent;}cur->_left = parent;Node* ppnode = parent->_parent;parent->_parent = cur;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}}void RotateR(Node* parent){++_rotateCount;Node* cur = parent->_left;Node* curright = cur->_right;parent->_left = curright;if (curright)curright->_parent = parent;Node* ppnode = parent->_parent;cur->_right = parent;parent->_parent = cur;if (ppnode == nullptr){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}}根据构建红黑树的规则验证红黑树
1. 每个结点不是红色就是黑色
2. 根节点是黑色的
3. 如果一个节点是红色的,则它的两个孩子结点是黑色的
4. 对于每个结点,从该结点到其所有后代叶结点的简单路径上,均 包含相同数目的黑色结点
5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点) bool IsBalance(){return _IsBalance(_root);}// 根节点->当前节点这条路径的黑色节点的数量bool CheckColour(Node* root, int blacknum, int benchmark){if (root == nullptr){if (blacknum != benchmark)return false;return true;}if (root->_col == BLACK)//统计黑色用于判断每条路径黑色都相同{++blacknum;}if (root->_col == RED && root->_parent && root->_parent->_col == RED){//当前节点与父节点连续红色cout << root->_kv.first << "出现连续红色节点" << endl;return false;}return CheckColour(root->_left, blacknum, benchmark)&& CheckColour(root->_right, blacknum, benchmark);//递归遍历每条路径}bool _IsBalance(Node* root){//根据构建红黑树的规则进行判断if (root == nullptr)return true;if (root->_col != BLACK)//根不能为红{return false;}// //参考值,统计一条路径的黑色节点数int benchmark = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK)++benchmark;cur = cur->_left;}//通过检查每条路径的黑色节点数判断是否平衡return CheckColour(root, 0, benchmark);}求红黑树高度以及遍历红黑树
基本上就是同AVL树以及搜索二叉树相同的道理。
int Height(){return _Height(_root);}//中序遍历void Inorder(){_Inorder(_root);}int _Height(Node* root){if (root == nullptr)return 0;int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}//中序遍历子函数void _Inorder(Node* root){if (root == nullptr)return;_Inorder(root->_left);cout << root->_kv.first << " ";_Inorder(root->_right);}三、总体代码
#pragma once
#include<iostream>
using namespace std;enum Color
{RED,BLACK
};template<class K, class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Color _col;RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _col(RED){}
};template<class K, class V>
struct RBTree
{typedef RBTreeNode<K, V> Node;
public:bool Insert(const pair<K, V>& kv){if (_root == nullptr)//如果根节点为空则直接开辟一个节点作为根节点并且返回true{_root = new Node(kv);_root->_col = BLACK;return true;}Node* parent = nullptr;//后续遍历找位置以及旋转等Node* cur = _root;//遍历用while (cur) // 开始遍历到指定位置->其实就是到cur为空节点的地方{if (cur->_kv.first < kv.first)//要插入节点大于则往右遍历{parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first)//要插入节点小于于则往左遍历{parent = cur;cur = cur->_left;}else{return false;}}//默认新增节点给红色,防止给黑破坏平衡cur = new Node(kv);cur->_col = RED;if (parent->_kv.first < kv.first)//同父节点比大小{parent->_right = cur;//链接新节点}else{parent->_left = cur;//链接新节点}cur->_parent = parent;//新节点链接父节点//根据红黑树特性开始调整while (parent && parent->_col == RED)//由于子节点和父节点都是红色,则需要调整{Node* grandfather = parent->_parent;//储存爷爷节点,用于找舅舅节点以及变色甚至旋转if (parent == grandfather->_left){// g// p u// cNode* uncle = grandfather->_right;//如果父亲节点在爷爷的左则舅舅在右if (uncle && uncle->_col == RED)//情况一:“变色处理” 舅舅节点存在且为红色,则我们需要将父亲以及舅舅变黑,爷爷变红{// 变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续向上处理cur = grandfather;parent = cur->_parent;}else //情况二:“需要旋转(单旋?or双旋?)+变色处理” 即舅舅节点存在时为黑或者舅舅节点不存在,则我们需要进行相应的旋转{if (cur == parent->_left){// 单旋// g p // p -> c g// cRotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// 双旋// g g p // p -> c -> c g// c pRotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}else // parent == grandfather->_right{// g// u p // c//Node* uncle = grandfather->_left;//情况一,但是uncle在左// u存在且为红if (uncle && uncle->_col == RED){// 变色parent->_col = uncle->_col = BLACK;grandfather->_col = RED;// 继续向上处理cur = grandfather;parent = cur->_parent;}else//情况二:“需要旋转(单旋?or双旋?)+变色处理”{if (cur == parent->_right){// 单旋// g p // p -> g c// cRotateL(grandfather);grandfather->_col = RED;parent->_col = BLACK;}else{// g g c// u p -> u c -> g p// c p u//RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break;}}}_root->_col = BLACK;//将根处理成黑。因为插入向上处理会改变,但是当最后为根时改变后就不能进入循环,因此需要最后处理为黑return true;}void RotateL(Node* parent){++_rotateCount;Node* cur = parent->_right;Node* curleft = cur->_left;parent->_right = curleft;if (curleft){curleft->_parent = parent;}cur->_left = parent;Node* ppnode = parent->_parent;parent->_parent = cur;if (parent == _root){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}}void RotateR(Node* parent){++_rotateCount;Node* cur = parent->_left;Node* curright = cur->_right;parent->_left = curright;if (curright)curright->_parent = parent;Node* ppnode = parent->_parent;cur->_right = parent;parent->_parent = cur;if (ppnode == nullptr){_root = cur;cur->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = cur;}else{ppnode->_right = cur;}cur->_parent = ppnode;}}bool IsBalance(){return _IsBalance(_root);}int Height(){return _Height(_root);}//中序遍历void Inorder(){_Inorder(_root);}private:// 根节点->当前节点这条路径的黑色节点的数量bool CheckColour(Node* root, int blacknum, int benchmark){if (root == nullptr){if (blacknum != benchmark)return false;return true;}if (root->_col == BLACK)//统计黑色用于判断每条路径黑色都相同{++blacknum;}if (root->_col == RED && root->_parent && root->_parent->_col == RED){//当前节点与父节点连续红色cout << root->_kv.first << "出现连续红色节点" << endl;return false;}return CheckColour(root->_left, blacknum, benchmark)&& CheckColour(root->_right, blacknum, benchmark);//递归遍历每条路径}bool _IsBalance(Node* root){//根据构建红黑树的规则进行判断if (root == nullptr)return true;if (root->_col != BLACK)//根不能为红{return false;}// //参考值,统计一条路径的黑色节点数int benchmark = 0;Node* cur = _root;while (cur){if (cur->_col == BLACK)++benchmark;cur = cur->_left;}//通过检查每条路径的黑色节点数判断是否平衡return CheckColour(root, 0, benchmark);}int _Height(Node* root){if (root == nullptr)return 0;int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}//中序遍历子函数void _Inorder(Node* root){if (root == nullptr)return;_Inorder(root->_left);cout << root->_kv.first << " ";_Inorder(root->_right);}private:Node* _root = nullptr;public:int _rotateCount = 0;
};感谢你耐心的看到这里ღ( ´・ᴗ・` )比心,如有哪里有错误请踢一脚作者o(╥﹏╥)o!

给个三连再走嘛~
相关文章:

【数据结构】—红黑树(C++实现)
🎬慕斯主页:修仙—别有洞天 💜本文前置知识: AVL树 ♈️今日夜电波:Letter Song—ヲタみん 1:36━━━━━━️💟──────── 5:35 …...

内衣洗衣机和手洗哪个干净?高性价比内衣洗衣机推荐
通常来说,我们的内衣裤对卫生要求比较高,毕竟是贴身穿的,所以如果和一般的衣物一起洗,就怕会有细菌互相感染。所以很多用户为了内衣裤的卫生都会选择自己手动洗,但手洗一方面很费时间和人力,另一方面又很伤…...
TikTok与互动广告:品牌如何打破传统界限
随着数字时代的蓬勃发展,广告行业也经历了翻天覆地的变革。在这个变革的浪潮中,TikTok作为一款崭新的社交媒体平台,通过其独特的短视频形式为品牌提供了全新的互动广告机会。 本文将深入探讨TikTok与互动广告的结合,以及品牌如何…...

跟着Nature Communications学习Hisat-Trinity-PASA等分析流程
一边学习,一边总结,一边分享! 详细教程请访问: 组学分析流程 本期分析流程 Hisat2-SamtoolsTrinity_GG_denovoPASA… 本期教程文章 题目:Genomic insights into local adaptation and future climate-induced vulnerability of a keystone forest tree in East Asia H…...
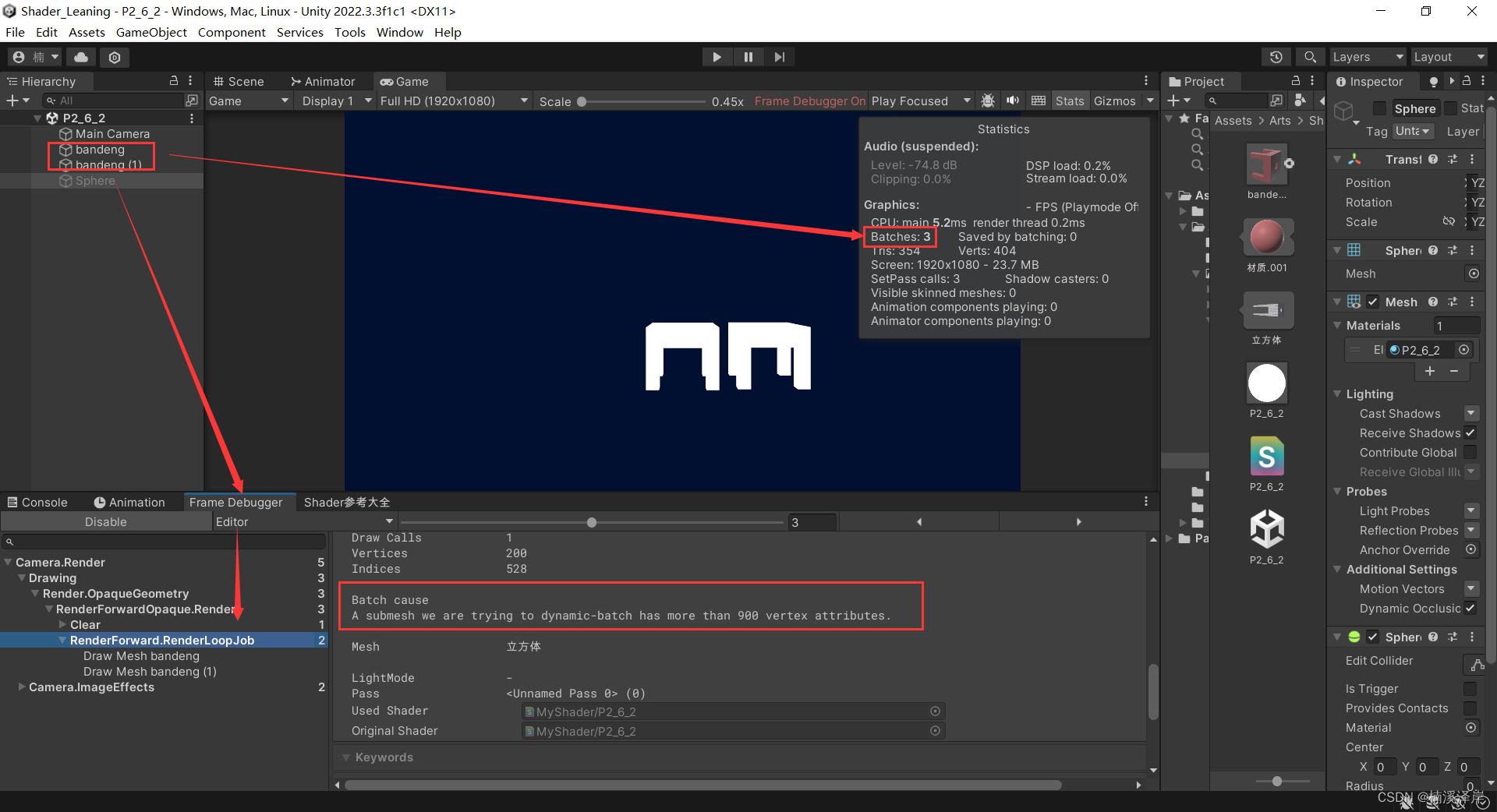
Unity中Batching优化的动态合批
文章目录 前言一、动态合批的规则1、材质相同是合批的前提,但是如果是材质实例的话,则一样无法合批。2、支持不同网格的合批3、动态合批需要网格支持的顶点条件二、我们导入一个模型并且制作一个Shader,来测试动态合批1、我们选择模型的 Mesh…...

2022年第十一届数学建模国际赛小美赛B题序列的遗传过程解题全过程文档及程序
2022年第十一届数学建模国际赛小美赛 B题 序列的遗传过程 原题再现: 序列同源性是指DNA、RNA或蛋白质序列之间的生物同源性,根据生命进化史中的共同祖先定义[1]。DNA、RNA或蛋白质之间的同源性通常根据它们的核苷酸或氨基酸序列相似性来推断。显著的相…...

【Linux】静态库与动态库制作及运行原理
Halo,这里是Ppeua。平时主要更新C语言,C,数据结构算法…感兴趣就关注我吧!你定不会失望。 本篇导航 0. 静态库与动态库1. 制作与使用静态库2. 制作与使用动态库3. 动态库是如何被加载到内存?3.1程序地址空间 0. 静态库…...

工具站推荐
自己搭了一个文本工具站 TextTool,包含了常用的文本功能。 我自己比较常用 行转列、列转行、下划线替换的功能。 欢迎各位大佬提意见和建议...
无法精准保留小数的解决方案)
【JS】toFixed()无法精准保留小数的解决方案
情景复现: 发现用 toFiexd() 四舍五入保留小数有时不是很精确,接下来用 a 8.0345,b8.045,举例如下: var a 8.035; console.log(a.toFixed(2)) // 8.04 var b 8.045; console.log(b.toFixed(2)) // 8.04 不难看出…...

vue3版本学习
1,响应式ref或者reactive const aa ref(hello) const bb reactive({ aa: hello, ss: workd }) 2,计算属性 响应式属性经过计算得到的值(ref),放到模板中,只会随着响应式author.books属性变化而变化 const autor …...
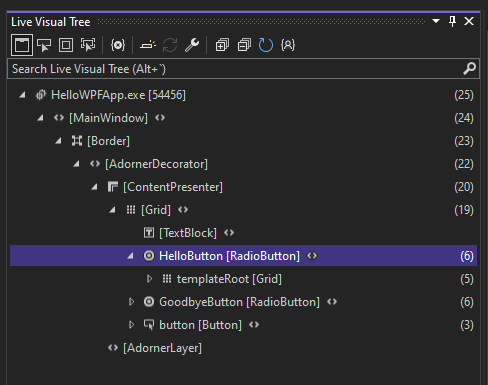
【WPF.NET开发】创建简单WPF应用
本文内容 先决条件什么是 WPF?配置 IDE创建项目设计用户界面 (UI)调试并测试应用程序 通过本文你将熟悉在使用 Visual Studio 开发应用程序时可使用的许多工具、对话框和设计器。 你将创建“Hello, World”应用程序、设计 UI、添加代码并调试错误。在此期间&#…...
视频智能分析国标GB28181云平台EasyCVR加密机授权异常是什么原因?
国标GB28181视频汇聚/视频云存储/集中存储/视频监控管理平台EasyCVR能在复杂的网络环境中,将分散的各类视频资源进行统一汇聚、整合、集中管理,实现视频资源的鉴权管理、按需调阅、全网分发、云存储、智能分析等。 近期有用户选择使用加密机进行EasyCVR授…...
Mysql安全之基础合规配置
一、背景 某次某平台进行安全性符合型评估时,列出了数据库相关安全选项,本文特对此记录,以供备忘参考。 二、安全配置 2.1、数据库系统登录时的用户进行身份标识和鉴别; 1)对登录Mysql系统用户的密码复杂度是否有要…...

前后端分离项目跨域请求
一、前端vue项目 在项目中创建request.js文件,添加以下内容 import axios from "axios"; const api axios.create({ //这里配置的是后端服务提供的接口baseURL: "http://localhost:8080/web-demo",timeout: 1000} ); export default api; …...
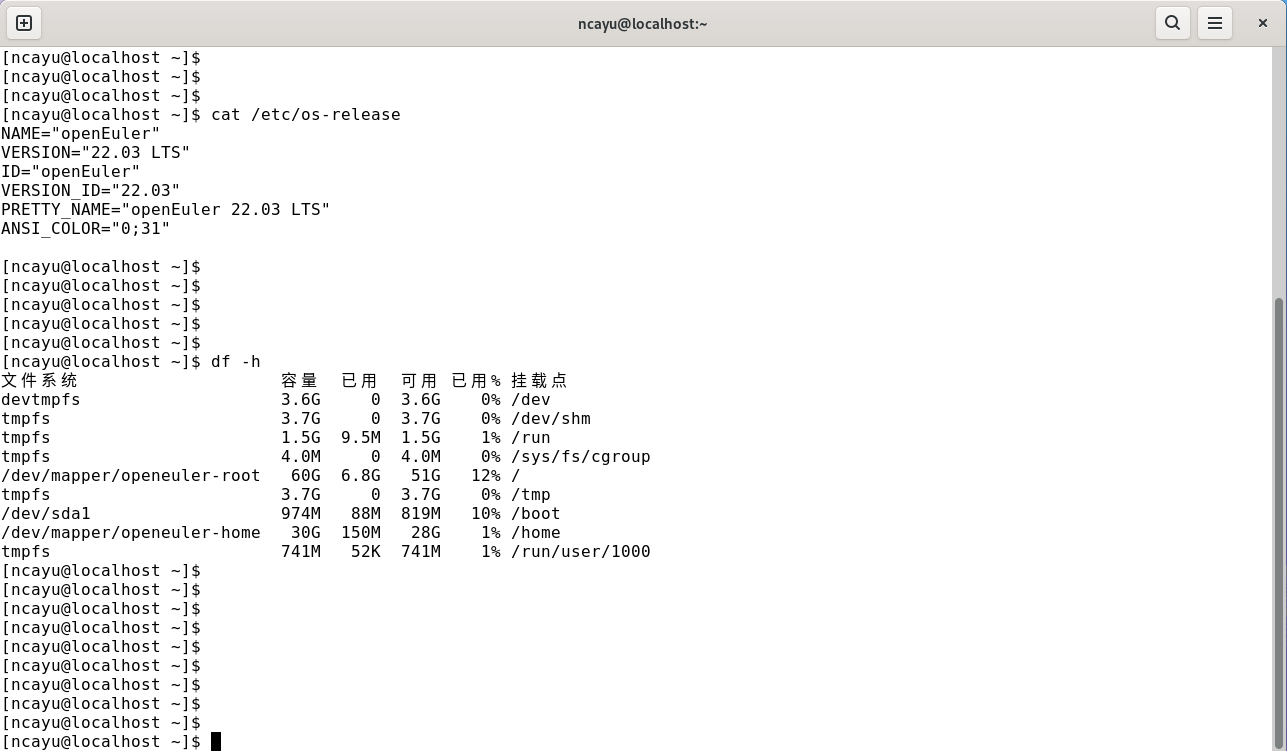
OpenEuler系统桌面终端设置字体
初始界面 终端的字体间距过大,阅读起来不方便。 调整终端字体 点击菜单,选择“配置文件首选项” 未命名 ---- 文本---- 勾选 自定义字体 ---- 选择 "DejaVu LGC Sans Mono"字体 你也可以根据自己的喜好,选择其他字体。 修改好了…...
)
repo常用命令解析(持续更新)
1 同步 1.1 将本地仓库更新到最新状态。它会从远程服务器下载最新的代码,并将本地仓库与之同步。如果本地仓库中已经存在某个项目,repo sync会自动检测本地仓库中该项目的版本,并将其更新到最新状态。 类似于git fetch和git merge命令组合使…...

关于小红书商单变现的一些答疑
AI小红书商单训练营也过去1个月了,今天给大家汇总几个常遇到的问题,希望对大家在运营过程中有所帮助。 1.账号封面是否要统一模版? 为了让账号主页呈现整洁美观的效果,建议统一封面设计,视频开头可以设置一个固定画面…...
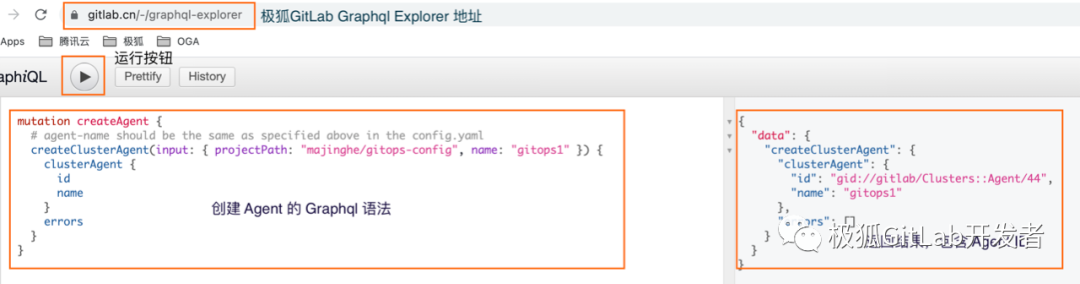
使用 Kubernetes Agent Server 实现 GitOps
目录 温习 GitOps 极狐GitLab Kubernetes Agent 极狐GitLab GitOps workflow 极狐GitLab KAS 的配置 创建极狐GitLab agent 创建 agent token Kubernetes 上安装 agent(agentk) 极狐GitLab GitOps workflow 实践 写在最后 温习 GitOps GitOps …...
Day12 qt QMianWindow,资源文件,对话框,布局方式,常用ui控件
QMianWindow 概述 QMainWindow 是一个为用户提供主窗口程序的类,包含一个菜单栏( menu bar )、多 个工具栏 (tool bars) 、多个铆接部件 (dock widgets) 、一个状态栏 (status bar) 及 一个中心部件 (central widget) 许多应用程序的基础…...
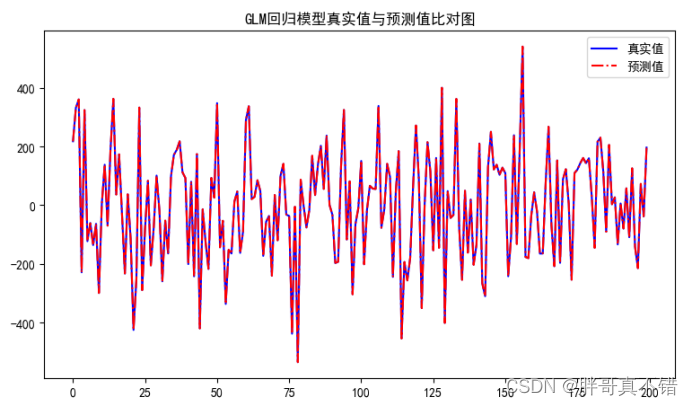
Python实现广义线性回归模型(statsmodels GLM算法)项目实战
说明:这是一个机器学习实战项目(附带数据代码文档视频讲解),如需数据代码文档视频讲解可以直接到文章最后获取。 1.项目背景 广义线性模型(Generalized Linear Model,简称GLM)是一种广泛应用于回归分析和分类问题的统…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

Linux 内存管理实战精讲:核心原理与面试常考点全解析
Linux 内存管理实战精讲:核心原理与面试常考点全解析 Linux 内核内存管理是系统设计中最复杂但也最核心的模块之一。它不仅支撑着虚拟内存机制、物理内存分配、进程隔离与资源复用,还直接决定系统运行的性能与稳定性。无论你是嵌入式开发者、内核调试工…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...
