【开放集检测OSR】开放集检测和闭集检测的区别和联系:从模型角度进行理解
定义一个分类器:
D t r a i n = { ( x i , y i ) } i = 1 N ⊂ X × C D_{train} = \{(x_i, y_i)\}^N _{i=1} ⊂ X × C Dtrain={(xi,yi)}i=1N⊂X×C
- X:输入空间
- ( x i , y i ) (x_i, y_i) (xi,yi): 输入的图像x以及其对象的类别标签y
- C :已知类的集合
1 For closed-set 闭集检测
测试时:用于测试模型性能的图像也都属于已知类别 C C C
D t e s t − c l o s e d = { ( x i , y i ) } i = 1 M ⊂ X × C D_{test-closed} = \{(x_i, y_i)\}^M _{i=1} ⊂ X × C Dtest−closed={(xi,yi)}i=1M⊂X×C
- 模型最终会返回一个概率分布: p ( y ∣ x ) p(y|x) p(y∣x)
分类器为每个输入示例x返回一个关于已知类别的概率分布 p ( y ∣ x ) p(y|x) p(y∣x),意味着对于给定的输入示例x,分类器会生成一个概率分布,其中每个类别y都对应一个概率值。这个概率值表示分类器对于该输入示例属于每个已知类别的置信度或可能性。
解析
具体而言,对于每个已知类别 c ∈ C c ∈ C c∈C,分类器会计算条件概率 p ( y = c ∣ x ) p(y=c|x) p(y=c∣x),表示在给定输入示例x的条件下,该示例属于类别c的概率。这样,对于每个输入示例x,分类器会为每个已知类别c生成一个概率值,最终形成一个概率分布 p ( y ∣ x ) p(y|x) p(y∣x),其中概率值的总和为1。
通过这个概率分布,我们可以了解分类器对于每个已知类别的相对置信度。通常情况下,预测类别会选择具有最高概率值的类别,因为它被认为是最有可能的类别。
这种概率分布的输出使我们能够获得更多关于分类器对于每个输入示例的不确定性和置信度的信息。它可以帮助我们进行后续的决策和分析,比如设置一个概率阈值来确定分类结果或者进行不确定性建模。
2 For open-set 开放集检测
测试时:用于测试模型性能的图像不仅仅属于已知类别 C C C,还可能属于位置类别 U U U
D t e s t − o p e n = { ( x i , y i ) } i = 1 M ′ ⊂ X × ( C ⋃ U ) D_{test-open} = \{(x_i, y_i)\}^{M'} _{i=1} ⊂ X × (C \bigcup U) Dtest−open={(xi,yi)}i=1M′⊂X×(C⋃U)
-
返回的概率分布: p ( y ∣ x , y ⊂ C ) p(y|x,y\subset C) p(y∣x,y⊂C) over known classes (理解:输入的图像为已知类的概率)
-
返回一个分数score: S ( y ∈ C ∣ x ) S(y\in C|x) S(y∈C∣x) indicate whether or not the test sample belongs to any of the known classes.
解析
在这种情况下,模型需要处理两种情况:已知类别和未见类别。
-
对于已知类别 C C C,模型会计算条件概率 p ( y ∈ C ∣ x ) p(y ∈ C|x) p(y∈C∣x),表示在给定输入示例x的条件下,该示例属于任何已知类别的概率。这样,模型可以返回一个关于已知类别的概率分布 p ( y ∣ x , y ∈ C ) p(y|x, y ∈ C) p(y∣x,y∈C),用于表示模型对于每个已知类别的置信度。
-
同时,模型还会返回一个分数 S ( y ∈ C ∣ x ) S(y ∈ C|x) S(y∈C∣x),该分数用于指示测试样本是否属于任何已知类别。 这个分数可以是一个连续值或二进制值,表示测试样本属于已知类别的程度。较高的分数表明测试样本更有可能属于已知类别,而较低的分数则表明测试样本可能属于未见类别 U U U。
3 关于概率分布 p ( y ∣ x ) 和 p ( y ∣ x , y ∈ C ) p(y|x)和p(y|x, y ∈ C) p(y∣x)和p(y∣x,y∈C)
关系:
- p(y|x):表示在给定输入示例x的条件下,该示例属于类别y的概率。这是一个针对已知类别的条件概率分布,在封闭集合的情景下使用。
- p(y|x, y ∈ C):表示在给定输入示例x的条件下,该示例属于任何已知类别y的概率。这也是一个针对已知类别的条件概率分布,但在开放集合的情景下使用。
区别:
- 范围:概率分布p(y|x)仅考虑已知类别C,而概率分布p(y|x, y ∈ C)同时考虑已知类别C和未知类别U。
- 输出:概率分布p(y|x)仅给出关于已知类别的概率信息,而概率分布p(y|x, y ∈ C)还会给出关于已知类别的分数信息,用于指示测试样本是否属于已知类别。
- 用途:概率分布p(y|x)主要用于封闭集合的分类任务,而概率分布p(y|x, y ∈ C)主要用于开放集合的分类任务,可以处理未见过的类别U。
相关文章:

【开放集检测OSR】开放集检测和闭集检测的区别和联系:从模型角度进行理解
定义一个分类器: D t r a i n { ( x i , y i ) } i 1 N ⊂ X C D_{train} \{(x_i, y_i)\}^N _{i1} ⊂ X C Dtrain{(xi,yi)}i1N⊂XC X:输入空间 ( x i , y i ) (x_i, y_i) (xi,yi): 输入的图像x以及其对象的类别标签yC :已知…...
【Flink】Flink核心概念简述
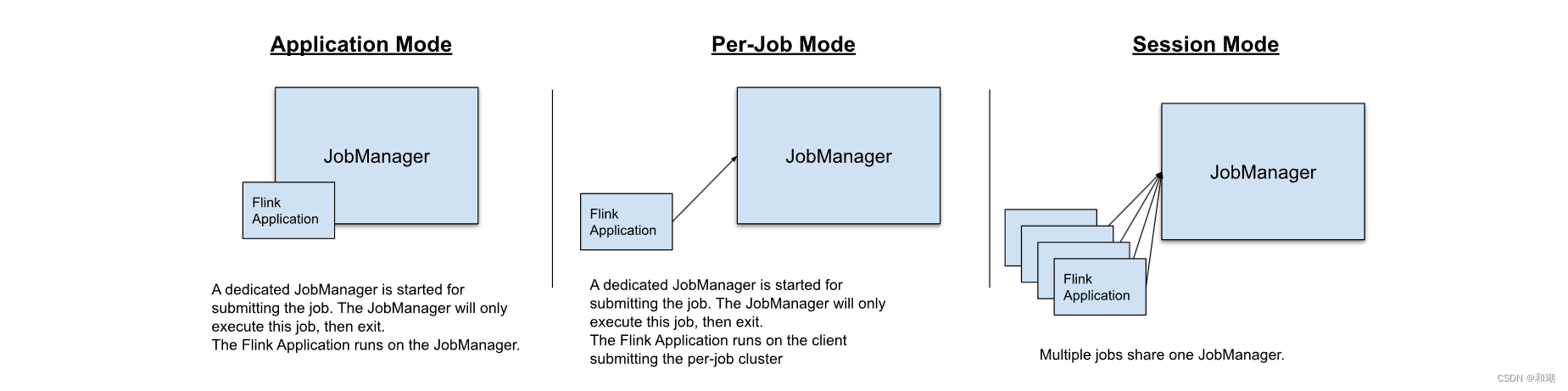
目录 一、Flink 简介二、Flink 组件栈1. API & Libraries 层2. runtime层3. 物理部署层 三、Flink 集群架构四、Flink基本编程模型五、Flink 的部署模式六、Flink 任务的执行模式五、Flink 的优点 一、Flink 简介 Apache Flink 的前身是柏林理工大学一个研究性项目&#x…...

linux-tar命令、解压、压缩
压缩 文件夹 命令:tar -zcvf ~/test/tar_t.tar.gz /target/ 将/target/文件夹及其子文件夹和文件压缩成tar_t.tar.gz文件,并放于~/test/路径下 文件 命令:tar -zcvf ~/test/tar_t.tar.gz /target/file 将/target/file文件压缩成tar_t.tar…...

Kafka Connect :构建强大分布式数据集成方案
Kafka Connect 是 Apache Kafka 生态系统中的关键组件,专为构建可靠、高效的分布式数据集成解决方案而设计。本文将深入探讨 Kafka Connect 的核心架构、使用方法以及如何通过丰富的示例代码解决实际的数据集成挑战。 Kafka Connect 的核心架构 Kafka Connect 的核…...

基于 Flink CDC 构建 MySQL 的 Streaming ETL to MySQL
简介 CDC 的全称是 Change Data Capture ,在广义的概念上,只要是能捕获数据变更的技术,我们都可以称之为 CDC 。目前通常描述的 CDC 技术主要面向数据库的变更,是一种用于捕获数据库中数据变更的技术。CDC 技术的应用场景非常广泛…...
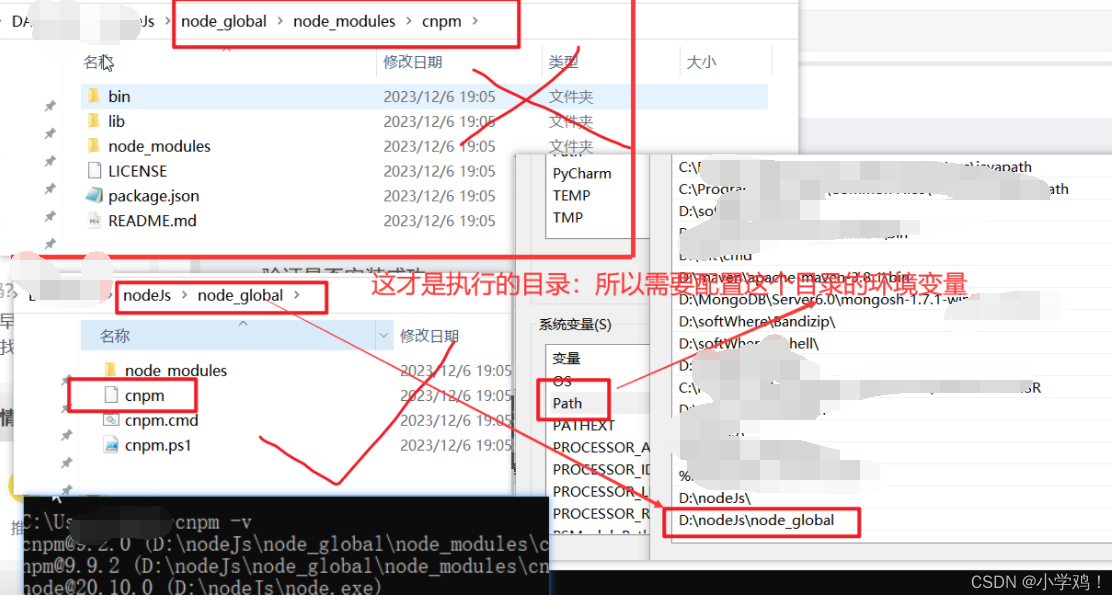
创建vue项目:node.js下载安装、配置环境变量,下载安装cnpm,配置npm的目录、镜像,安装vue、搭建vue项目开发环境(保姆级教程一)
今天讲解 Windows 如何创建 vue 项目,搭建 vue 开发环境,这是这个系列的第一章,有什么问题请留言,请点赞收藏!!! 文章目录 一、Vue简单介绍二、开始搭建1、安装node.js环境2、配置npm下载时的默…...
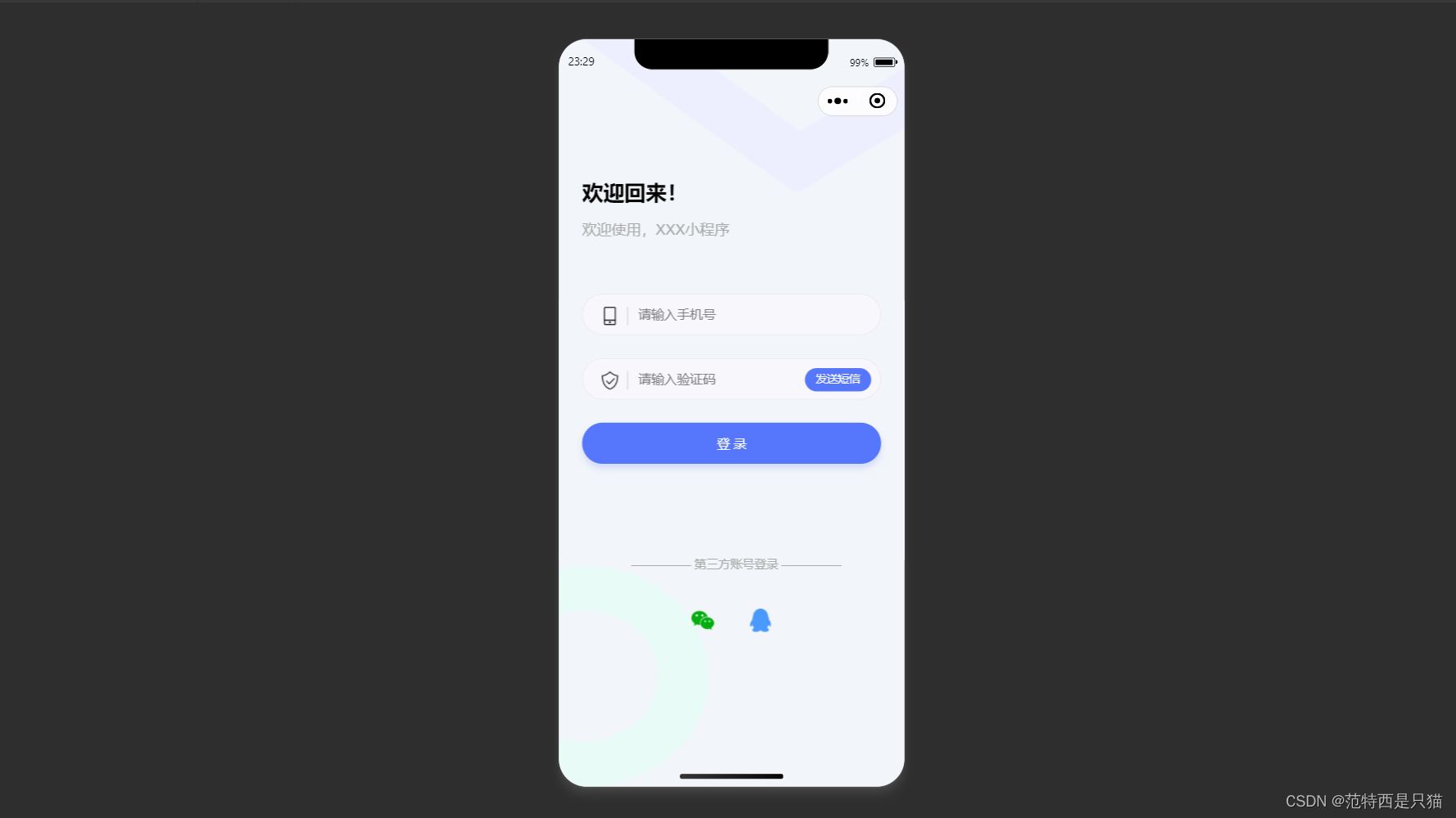
uni-app 微信小程序之好看的ui登录页面(一)
文章目录 1. 页面效果2. 页面样式代码 更多登录ui页面 uni-app 微信小程序之好看的ui登录页面(一) uni-app 微信小程序之好看的ui登录页面(二) uni-app 微信小程序之好看的ui登录页面(三) uni-app 微信小程…...

[ES]ElasticSearch强转日期的时区问题
问题 由于ES不能修改时区,且默认时区始终为UTC。 当才查询数据时,通过强转获得的日期并不是想要的,通过分析发现,正是由于默认时区导致结果相差了8个小时。 查询语句: POST http://localhost:9200/_sql?formattext {&…...

YOLOv5结合BiFPN,如何替换YOLOv5的Neck实现更强的检测能力?
一、BiFPN是什么? 1、什么是BiFPN BiFPN是一种基于特征金字塔网络(FPN)和双向特征金字塔网络(BiFPN)的对象检测神经网络结构,它被用于提高目标检测的准确度和速度。在目标检测领域,FPN用于将不同…...

3.PyTorch——常用神经网络层
import numpy as np import pandas as pd import torch as t from PIL import Image from torchvision.transforms import ToTensor, ToPILImaget.__version__2.1.13.1 图像相关层 图像相关层主要包括卷积层(Conv)、池化层(Pool)…...
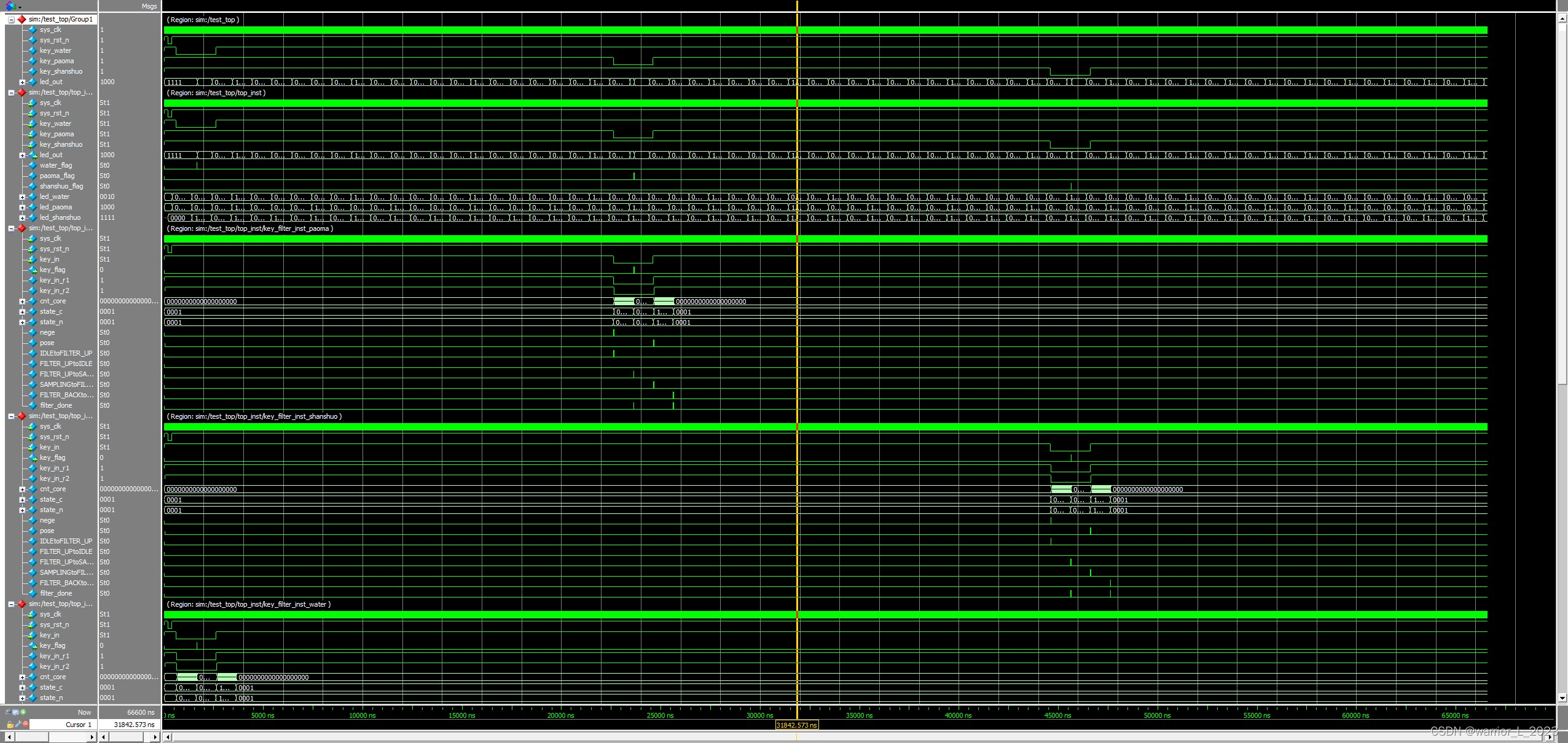
状态机的练习:按键控制led灯
设计思路: 三个按键控制led输出。 三个按键经过滤波(消抖),产生三个按键标志信号。 三个led数据的产生模块(流水,跑马,闪烁模块),分别产生led信号。 这六路信号(三路按键信号&am…...

看图学源码之 CopyOnWriteArraySet源码分析
基本介绍 使用内部CopyOnWriteArrayList进行所有操作的Set 特点 它最适合以下应用程序:集合大小通常较小、只读操作的数量远远多于可变操作,并且您需要在遍历期间防止线程之间的干扰。它是线程安全的。突变操作( add 、 set 、 remove等&…...

almaLinux centos8 下载ffmpeg离线安装包、离线安装
脚本 # 添加RPMfusion仓库 sudo yum install https://download1.rpmfusion.org/free/el/rpmfusion-free-release-8.noarch.rpm wget -ymkdir -p /root/ffmpeg cd /root/ffmpegwget http://rpmfind.net/linux/epel/7/x86_64/Packages/s/SDL2-2.0.14-2.el7.x86_64.rpmyum instal…...

CSS3 属性: transition过渡 与 transform动画
CSS3 提供了很多强大的功能,使开发人员可以创建更加吸引人的视觉效果,而不需要依赖于 JavaScript 或 Flash。其中,transition 和 transform 是两个常用的属性,它们分别用于创建平滑的过渡效果和元素的变形效果。下面我们将详细介绍…...

TCP通讯
第二十一章 网络通信 本章节主要讲解的是TCP和UDP两种通信方式它们都有着自己的优点和缺点 这两种通讯方式不通的地方就是TCP是一对一通信 UDP是一对多的通信方式 接下来会一一讲解 TCP通信 TCP通信方式呢 主要的通讯方式是一对一的通讯方式,也有着优点和缺点 …...

(NeRF学习)3D Gaussian Splatting Instant-NGP
学习参考: 3D Gaussian Splatting入门指南【五分钟学会渲染自己的NeRF模型,有手就行!】 三维重建instant-ngp环境部署与colmap、ffmpeg的脚本参数使用 一、3D Gaussian Splatting (一)3D Gaussian Splatting环境配置…...
uni-app 微信小程序之好看的ui登录页面(三)
文章目录 1. 页面效果2. 页面样式代码 更多登录ui页面 uni-app 微信小程序之好看的ui登录页面(一) uni-app 微信小程序之好看的ui登录页面(二) uni-app 微信小程序之好看的ui登录页面(三) uni-app 微信小程…...

Android 默认打开应用的权限
有项目需要客户要安装第三方软件,但是要手动点击打开权限,就想不动手就打开。 //安装第三方软件,修改方式 frameworks\base\services\core\java\com\android\server\pm\PackageManagerService.java //找到如下源码: //有三种方…...

2023年广东工业大学腾讯杯新生程序设计竞赛
E.不知道叫什么名字 题意:找一段连续的区间,使得区间和为0且区间长度最大,输出区间长度。 思路:考虑前缀和,然后使用map去记录每个前缀和第一次出现的位置,然后对数组进行扫描即可。原理:若 s …...
如何访问Github下载FFmpeg源码)
FFmpeg开发笔记(六)如何访问Github下载FFmpeg源码
学习FFmpeg的时候,经常要到GitHub下载各种开源代码,比如FFmpeg的源码页面位于https://github.com/FFmpeg/FFmpeg。然而国内访问GitHub很不稳定,经常打不开该网站,比如在命令行执行下面的ping命令。 ping github.com 上面的ping结…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...
