刷题记录--算法--简单
第一题
2582. 递枕头
已解答
简单
相关标签
相关企业
提示
n 个人站成一排,按从 1 到 n 编号。
最初,排在队首的第一个人拿着一个枕头。每秒钟,拿着枕头的人会将枕头传递给队伍中的下一个人。一旦枕头到达队首或队尾,传递方向就会改变,队伍会继续沿相反方向传递枕头。
- 例如,当枕头到达第
n个人时,TA 会将枕头传递给第n - 1个人,然后传递给第n - 2个人,依此类推。
给你两个正整数 n 和 time ,返回 time 秒后拿着枕头的人的编号。
示例 1:
输入:n = 4, time = 5 输出:2 解释:队伍中枕头的传递情况为:1 -> 2 -> 3 -> 4 -> 3 -> 2 。 5 秒后,枕头传递到第 2 个人手中。
示例 2:
输入:n = 3, time = 2 输出:3 解释:队伍中枕头的传递情况为:1 -> 2 -> 3 。 2 秒后,枕头传递到第 3 个人手中。
分析思路:
题目有两个参数time 与n
先分析time参数,有两种可能为0和不为0
time为0,没有时间,不计算后面的数。
time不为0,有时间,需要计算后面的数。
再分析n参数,从题目已知有两种可能n>1和n<1
n>1,数据会随time的变化而变化
n<=1,数据不会随time的变化而变化
最后分析time与n的关系
time与n有三种关系
time>n,会发生往复计数的情况。
time=n,会发生往复计数的情况,但结果一定是n-1啦。
time<n,不会发生往复计数的情况。
至此可以得到第一种解决方案
第一种解决方案数数法
按照先从1开始向右计数,到达n时调转方向向左计数的方法,这种方法不需要考虑time为0的情况,需要屏蔽n为0的情况,需要屏蔽n<=1的情况。
设置一个以time为参数的while循环,当time为0时退出循环,设置flag表明方向,1为向右,2为向左。设置i作为计数参数,程序开始时i为1向右计数,当i等于n时,flag变为-1,i向左计数。
需要注意的是,把n<2剔除。
class Solution {
public:int passThePillow(int n, int time){int i=1;int flag=1;if(n<2){i=n;}else{while(time){if(flag==1){++i;if(i==n){flag=-1;}}else if(flag==-1){--i;if(i==1){flag=1;}}--time;}}return i;}
};但是第一种思路很挫,非常挫,特别挫,作为代码狗,怎么能看得上这种思路呢,这种屎山代码呢,而且还没用到分析三,相当于刚才的分析白分析啦,不能忍啊,凸(艹皿艹 )。
第二种思路 除余法(厨余垃圾),这种方法也很垃圾
除余法的思路来自于在有限的线段下,除法的结果代表需要往复的次数,余的结果代表他还要走几次,举个栗子。
n=4,time=5

注意一下这里,time=5的意思是从5开始,走到0为止,体现在i上,是i要在1之后走出5步。上面的图表现出time=5时走出了一个往复,用除法体现5/3=1(这里必须是除3也就是n-1,因为向右前进时i只走了三步),剩下的两部5%3=2,所以n=4,time=5时,i走了一个往复,先向右走到4,然后调头走到2,这里的5/3=1的1表示的i走完一个全程(全程指的是1到4,或者4到1,不管方向,总之1代表走完一个全程,就是这样凸(艹皿艹 )这特么的这么难写,凸(艹皿艹 )啊);
上面写了一段,总结一下就是5/3=1表示i走完一段全程,5%3=2表示走完全程之后再走两步。
确定上面的以后,需要判断方向,以5/3为例,走完一个全程,需要调头,这时候的方向是向左的。所以不能被2整除的此时是向左。
接下来以7/3为例

7/3等于2,此时已经走完两个全程,方向向右。
接下来的余就简单啦,当(time/(n-1))%2==0时,向右走,此时只需要1+time%(n-1),相反(time/(n-1))%2!=0时向左走,用n-time%(n-1)就好了。
上面是time>n 的情况,接下来看看time=n的情况。
time=n表示走完一个全程多走一步,实际上也是一个全程以上的问题,可以归类到上面。
time<n这是一个没有走完全程的情况,不走完全程时,方向是向右的,那么完全可以带入多个全程的情况,(time/(n-1))%2==0。
接下来看看n,n分为<=1和>1两种情况,n<=1这种情况需要剔除,因为题目给的数从2开始,这个就不写了,也就一个if的事。
再接下来,就是time为0的情况,emmmmmm。。。。。time为0时,完全不影响i=1+time%(n-1);i=n-time%(n-1);计算的结果,所以这个题目的代码是
class Solution {
public:int passThePillow(int n, int time) {int i=0;if((time/(n-1))%2!=0){i=n-time%(n-1);}else if((time/(n-1))%2==0){i=1+time%(n-1);}return i;}
};不用循环,但是懒得想,厨余垃圾啊
最后看一下官方题解,目前么想明白
我们注意到每经过 2×(n−1)2 \times (n - 1)2×(n−1) 的时间,枕头会被传递回起点,所以我们可以直接用 time\textit{time}time 对 2×(n−1)2 \times (n - 1)2×(n−1) 取模求余数。
如果 time<n\textit{time} < ntime<n,枕头没有传递到队尾,传递到 time+1\textit{time} + 1time+1。
如果 time≥n\textit{time} \ge ntime≥n,枕头已经传递过队尾,传递到 n−(time−(n−1))=n×2−time−1n - (\textit{time} - (n - 1)) = n \times 2 - \textit{time} - 1n−(time−(n−1))=n×2−time−1。
相关文章:

刷题记录--算法--简单
第一题 2582. 递枕头 已解答 简单 相关标签 相关企业 提示 n 个人站成一排,按从 1 到 n 编号。 最初,排在队首的第一个人拿着一个枕头。每秒钟,拿着枕头的人会将枕头传递给队伍中的下一个人。一旦枕头到达队首或队尾,传递…...
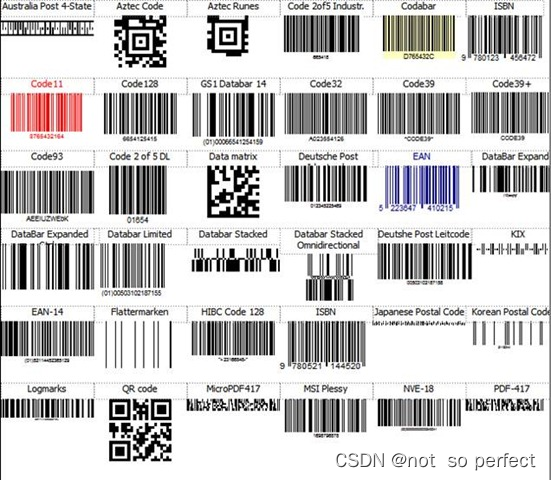
条码生成器与Zint使用
文章目录 目的条形码zint支持条形码种类下载编译qt pro配置code保存条形码目的 1: 了解条形码数据理论知识 2: 了解zint第三方库相关, 如何编译引用到项目中 条形码 条形码(Barcode)一维码 和二维码(QR code)都是用于存储信息的图形化表示方式,通常应用于商品标识、库…...
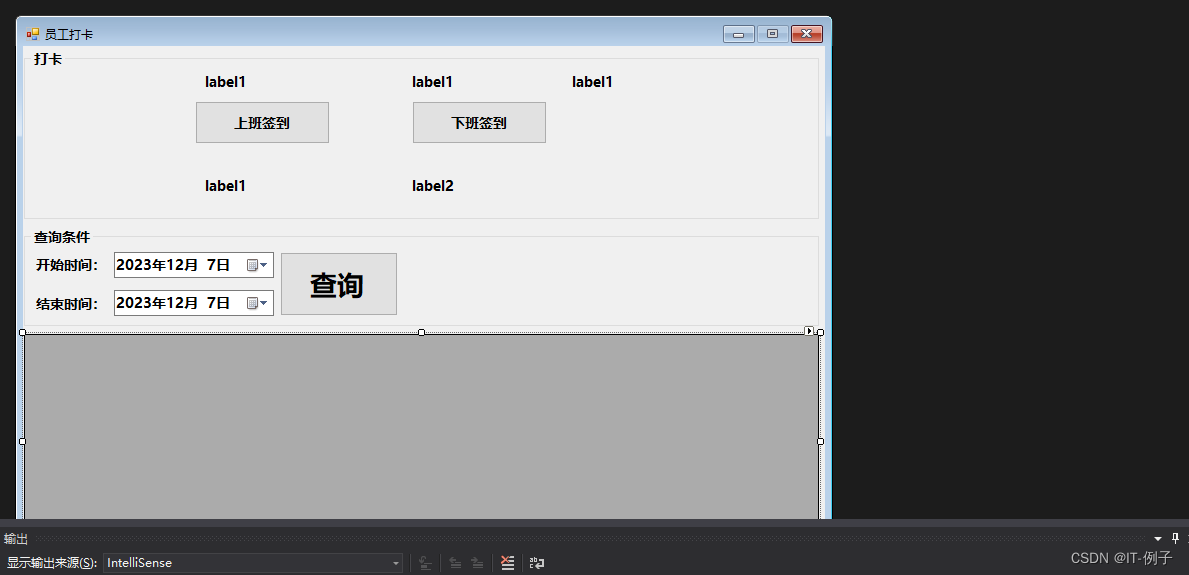
C#winform上下班打卡系统Demo
C# winform上下班打卡系统Demo 系统效果如图所示 7个label控件(lblUsername、lblLoggedInEmployeeId、lab_IP、lblCheckOutTime、lblCheckInTime、lab_starttime、lab_endtime)、3个按钮、1个dataGridView控件、2个groupBox控件 C#代码实现 using System; using System.Dat…...

P1 Qt的认识及环境配置
目录 前言 01 下载Qt Creator windows下载安装包拷贝到Linux Linux直接下载 02 Linux 安装Qt 前言 🎬 个人主页:ChenPi 🐻推荐专栏1: 《C_ChenPi的博客-CSDN博客》✨✨✨ 🔥 推荐专栏2: 《Linux C应用编程(概念类…...

单元测试Nunit的几种断言
Nunit提供了一些辅助函数用于确定好某个被测试函数是否正常工作。通常把这些函数称为断言 断言是单元测试最基本的组成部分。因此,NUnit程序库以Assert类的静态方法的形式提供了不同形式的多种断言 1. Assert.AreEqual:比较两个值是否相等。用于比较数…...

前端中的响应式布局与各个端适配
什么是响应式布局? 响应式布局指的是同一页面在不同屏幕尺寸下有不同的布局。在移动互联网高度发达的今天,我们在桌面浏览器上开发的网页已经无法满足在移动设备上查看的需求。传统的开发方式是PC端开发一套页面,手机端再开发一套页面。但是…...
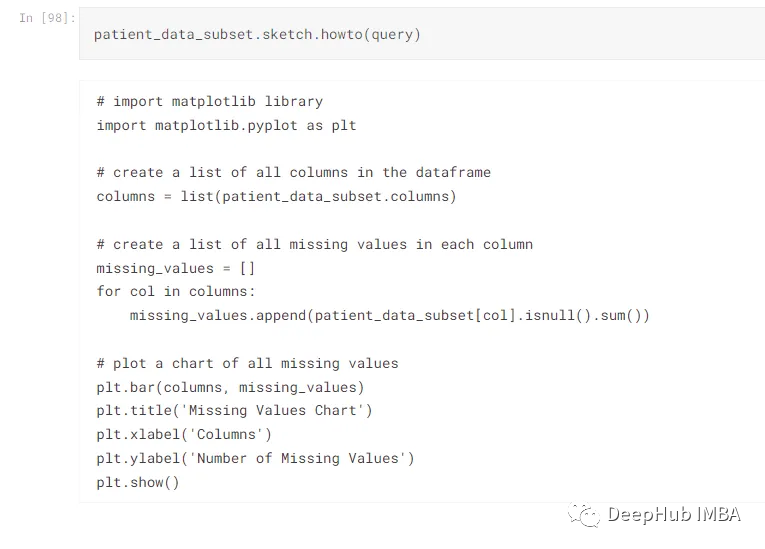
2023年5个自动化EDA库推荐
EDA或探索性数据分析是一项耗时的工作,但是由于EDA是不可避免的,所以Python出现了很多自动化库来减少执行分析所需的时间。EDA的主要目标不是制作花哨的图形或创建彩色的图形,而是获得对数据集的理解,并获得对变量之间的分布和相关…...

7-1 查找书籍
给定n本书的名称和定价,本题要求编写程序,查找并输出其中定价最高和最低的书的名称和定价。 输入格式: 输入第一行给出正整数n(<10),随后给出n本书的信息。每本书在一行中给出书名,即长度不超过30的字…...

【无线网络技术】——无线广域网(学习笔记)
📖 前言:无线广域网(WWAN)是指覆盖全国或全球范围内的无线网络,提供更大范围内的无线接入,与无线个域网、无线局域网和无线城域网相比,它更加强调的是快速移动性。典型的无线广域网:蜂窝移动通信系统和卫星…...

【java+vue+微信小程序项目】从零开始搭建——健身房管理平台(2)后端跨域、登录模块、springboot分层架构、IDEA修改快捷键、vue代码风格
项目笔记为项目总结笔记,若有错误欢迎指出哟~ 【项目专栏】 【java+vue+微信小程序项目】从零开始搭建——健身房管理平台(1)spring boot项目搭建、vue项目搭建、微信小程序项目搭建 【java+vue+微信小程序项目】从零开始搭建——健身房管理平台(2)后端跨域、登录模块、sp…...

NGINX相关配置
全局配置 NGINX配置信息 nginx 官方帮助文档:http://nginx.org/en/docs/Nginx的配置文件的组成部分: 主配置文件:/conf/nginx.conf(/nginx/conf/nginx.conf) 子配置文件: include conf.d/*.conf#事件驱动相关的配置 同步 event { worker_…...
如何将idea中导入的文件夹中的项目识别为maven项目
问题描述 大家经常遇到导入某个文件夹的时候,需要将某个子文件夹识别为maven项目 解决方案...

CleanMyMac4.16中文最新版本下载
当很多人还在为电脑运行缓慢、工作问题不能快速得到解决而烦恼的时候,我已经使用过了多款系统清理工具,并找到了最适合我的那一款。我的电脑是超耐用的Mac book,接下来给大家介绍三种在众多苹果电脑清理软件的排名较高的软件。 一、Maintena…...

谷歌正式发布最强 AI 模型 Gemini
2023年12月6日,谷歌公司宣布推出其被认为是规模最大、功能最强大的人工智能模型 Gemini。 Gemini将分为三个不同的套件:Gemini Ultra、Gemini Pro和Gemini Nano。 Gemini Ultra被认为具备最强大的能力,Gemini Pro则可扩展至多任务&#x…...
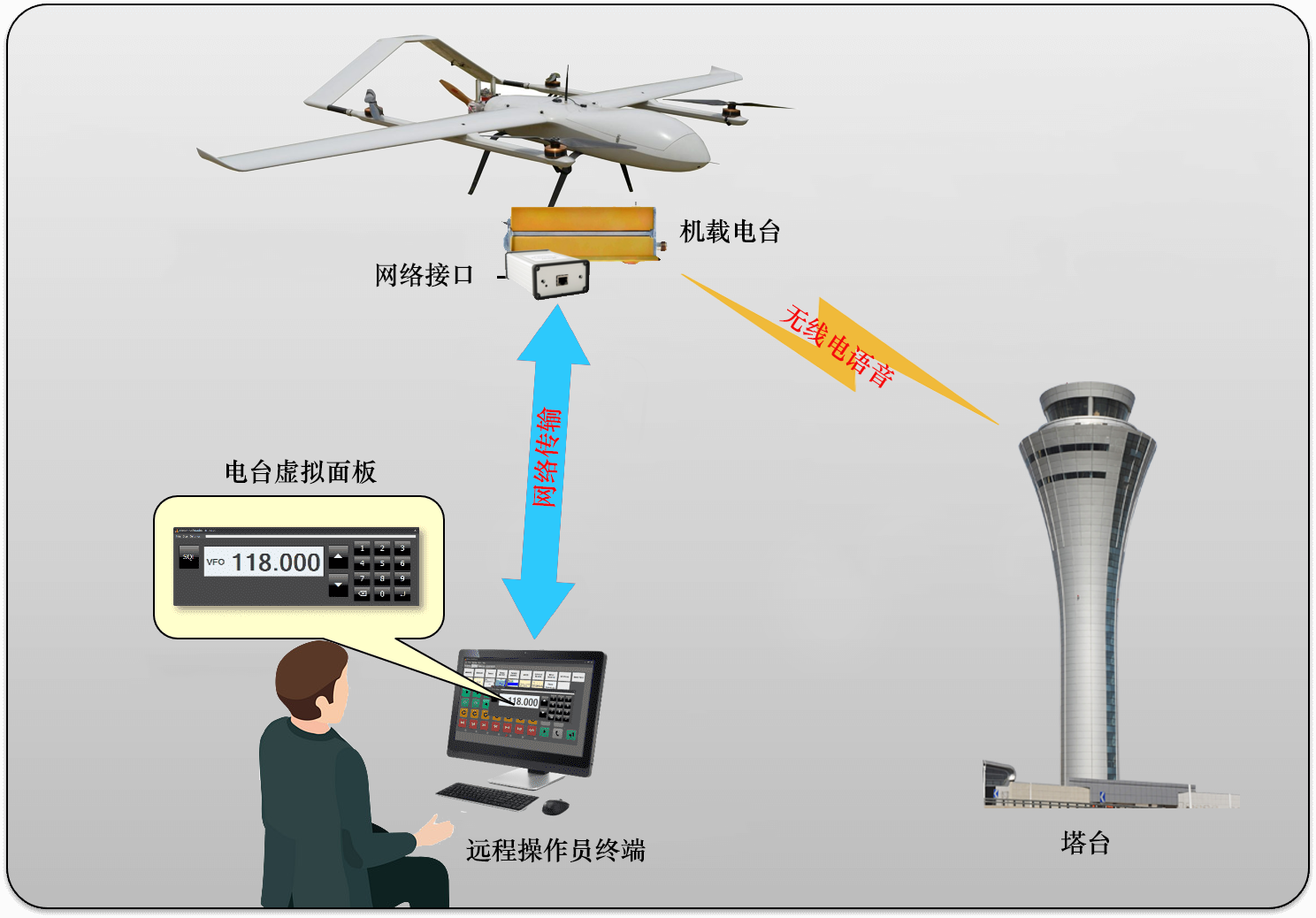
无人机语音中继电台 U-ATC118
简介 甚高频无线电中继通讯系统使用经过适航认证的机载电台连接数字网络传输模块,通过网络远程控制无缝实现无人机操作员与塔台直接语音通话。无人机操作员可以从地面控制站远程操作机载电台进行频率切换、静噪开关、PTT按钮,电台虚拟面板与真实面板布局…...

两种测量方式的自适应卡尔曼滤波数据融合
文章目录 测试效果代码CMakeLists.txt参考测试效果 代码 #include <iostream> #include <Eigen/Dense> #include...
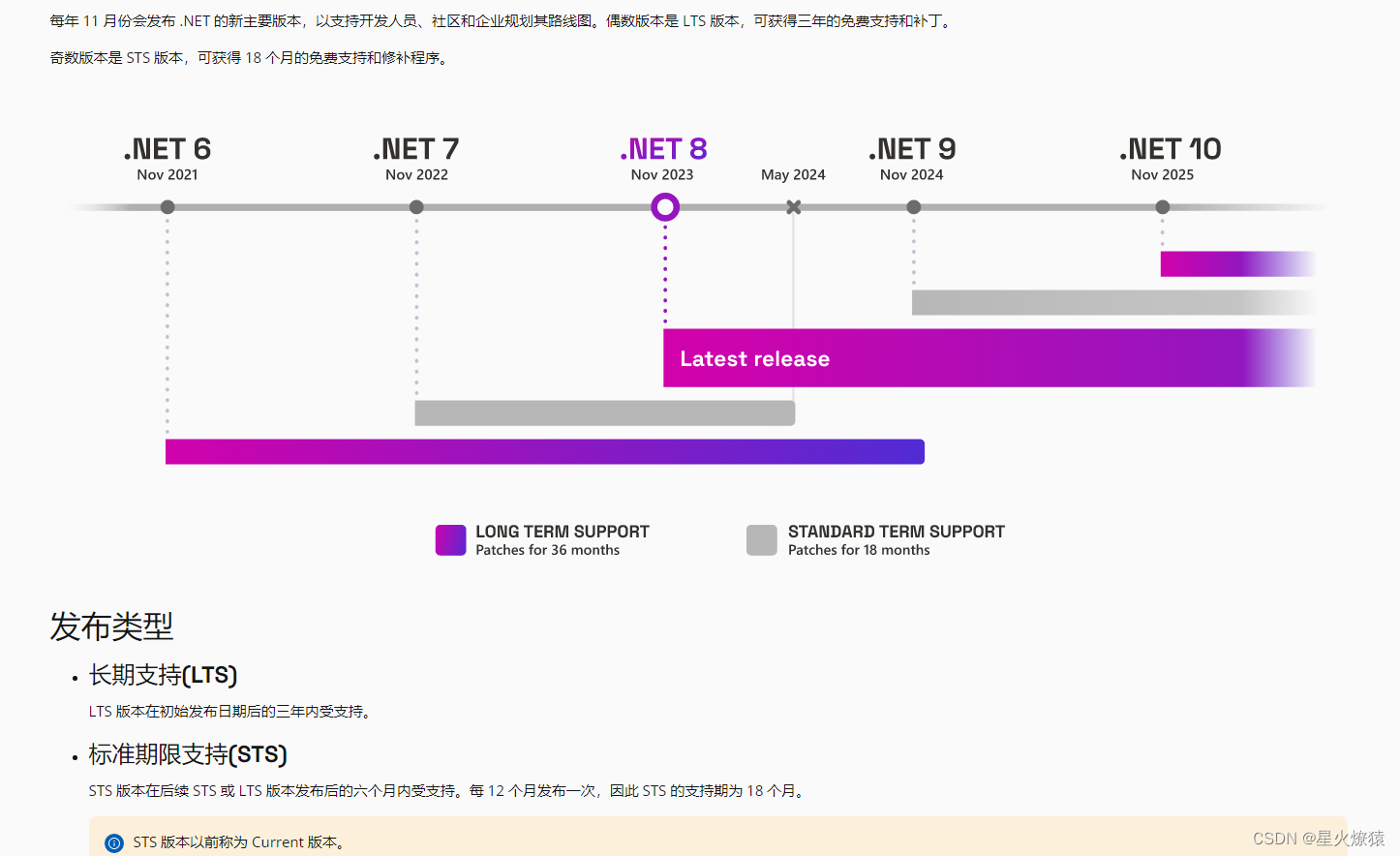
.Net6支持的操作系统版本(.net8已来,你还在用.netframework4.5吗)
机缘 不知不觉,.NET8都已经面世,而我们一直还停留在.netframework4.5开发阶段,最近准备抽空研究一下.Net6,一是为了提高技术积累,一方面想着通过这次的学习,看有没有可能将老的FX版本替换到.Net6开发上,经过查找官方资料,对.Net6支持的系统版本做一个分享,方便大家后期…...

CopyOnWriteArraySet怎么用
简介 CopyOnWriteArraySet是一个线程安全的无序集合,它基于“写时复制”的思想实现。它继承自AbstractSet,可以将其理解成线程安全的HashSet。 CopyOnWriteArraySet在读取操作比较频繁、写入操作相对较少的情况下可以提高程序的性能和可靠性。它的线程…...
uniapp得app云打包问题
获取appid,具体可以查看详情 也可以配置图标,获取直接生成即可 发行 打包配置 自有证书测试使用时候不需要使用 编译打包 最后找到安装包apk安装到手机 打包前,图片命名使用要非中文,否则无法打包成功会报错...

Linux bin包生成
需求背景: 在实际项目时我们很少把源码用个tar给到客户,这样显得很不专业,且有的时候我们提供补丁,那么这个时候我们提供一个补丁的bin包可以直接安装运行就显得很高大上了。 物料准备 准备一台liunx,虚拟机亦可&am…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...
