如何选择一款安全可靠的跨网安全数据交换系统?
随着网络和数据安全的重视程度增加,为了有效地保护内部的核心数据资产,普遍会采用内外网隔离的策略。像国内的政府机构、金融、能源电力、航空航天、医院等关乎国计民生的行业和领域均已进行了网络的隔离,将内部划分成不同的网段,比如内网-外网;研发网-办公网等等,将重要的数据代码放在内部网络,禁止用户访问或带出隔离网,从而保证数据资产的安全性。但是网络隔离后,不同网段间,仍存在数据交换需求,这时就需要一款安全数据交换系统,来进行文件安全交换。

很多企业会使用FTP来完成文件的流转,但使用中却存在以下问题:
1.FTP属于明文传输,对用户的网络和数据安全行为构成威胁:漏洞频发,容易遭到DOS攻击;随手可得的免费客户端软件,为黑客提供了便利;数据在传输中容易被截获和窃取。
2.不同部门、不同人员对文件的使用和管理权限应不同,使用FTP传输无法实现对文件权限的精细化管理。
3.FTP传输的日志功能较弱,无法满足大部分企业的审计要求。
4.员工个人无法独立轻简地进行传输操作,技术部门需投入人力协助,导致人力成本和维护成本较高。
5.传输稳定性较弱,无法满足大文件可靠传输,一定程度上影响办公效率。
6.对于一些内部服务器和操作系统已经进行国产化替代部署的企业,FTP无法适配国产化操作环境。
基于上述问题点,企业需要一套专业、高效、稳定的安全数据交换系统,来解决隔离网间文件传输的困境。这里推荐一款《Ftrans跨网文件安全交换系统》,其主要作用是帮助企业和组织在隔离网络之间(例如研发网-办公网、生产网-测试网、内网-外网,等等),快速建立“统一、安全、 高效的数传通道”,有效防止敏感信息泄露。这款安全数据交换系统解决方案的价值和优势有以下几点:
一、统一用户跨网文件交换方式
构建企业内部统一、安全的跨网文件交换通道;解决了企业多工具、系统并行使用,文件交换行为分散,难以管控的问题。
二、安全可控,防止数据泄露
多种数据交换安全管控手段,安全策略灵活而强大,充分满足不同类型企业的安全需求,有效防止数据泄露。
三、合法合规,规避使用风险
针对跨网文件交换的数据和人员权限、数据审核、日志审计等均有明确而有效的管控措施, 符合法律法规要求,避免企业的合规风险。
四、易用便捷,业务部门轻松使用
三种跨网交换方式、人性化的功能设计、清晰简洁的使用界面,简单易理解易用,业务部门可独立自主便捷操作,充分释放IT部门人力投入。
五、高效可靠,提升业务效率
独有的私有高性能文件传输协议专利技术,提供专用的浏览器传输插件,可实现TB级超大文件、 百万级海量文件的可靠传输,让文件流转和业务高效开展。
六、贴合市场,专业品质保障
专注于企业级数据交换技术十余年,产品在多个行业200多家头部客户中进行应用,实时保障15万终端用户的日常使用,产品和服务品质更有保障。
总体来说,《Ftrans跨网文件安全交换系统》这款安全数据交换系统,可以帮助企业建立可管控可审计、防止信息泄露、安全合规的统一跨网文件交换通道。目前已应用于高科技、制造业、金融、医疗、能源、电力等多个行业,是解决网络隔离条件下,网间数据安全收发、摆渡、共享的理想解决方案。
相关文章:

如何选择一款安全可靠的跨网安全数据交换系统?
随着网络和数据安全的重视程度增加,为了有效地保护内部的核心数据资产,普遍会采用内外网隔离的策略。像国内的政府机构、金融、能源电力、航空航天、医院等关乎国计民生的行业和领域均已进行了网络的隔离,将内部划分成不同的网段,…...
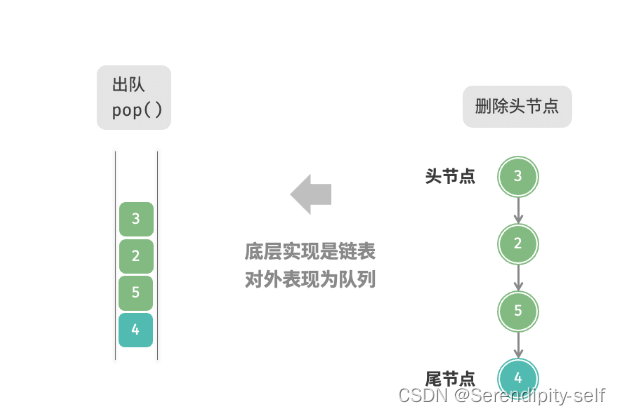
基于c++版本的数据结构改-python栈和队列思维总结
##栈部分-(叠猫猫) ##抽象数据类型栈的定义:是一种遵循先入后出的逻辑的线性数据结构。 换种方式去理解这种数据结构如果我们在一摞盘子中取到下面的盘子,我们首先要把最上面的盘子依次拿走,才可以继续拿下面的盘子&…...
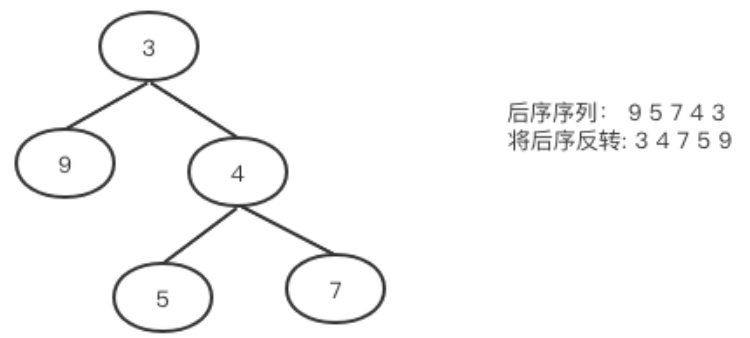
算法通关村第七关—迭代实现二叉树的遍历(黄金)
迭代实现二叉树的遍历 迭代法实现前序遍历 前序遍历是中左右,如果还有左子树就一直向下找。完了之后再返回从最底层逐步向上向右找。不难写出如下代码:(注意代码中,空节点不入栈) public List<Integer>preorde…...
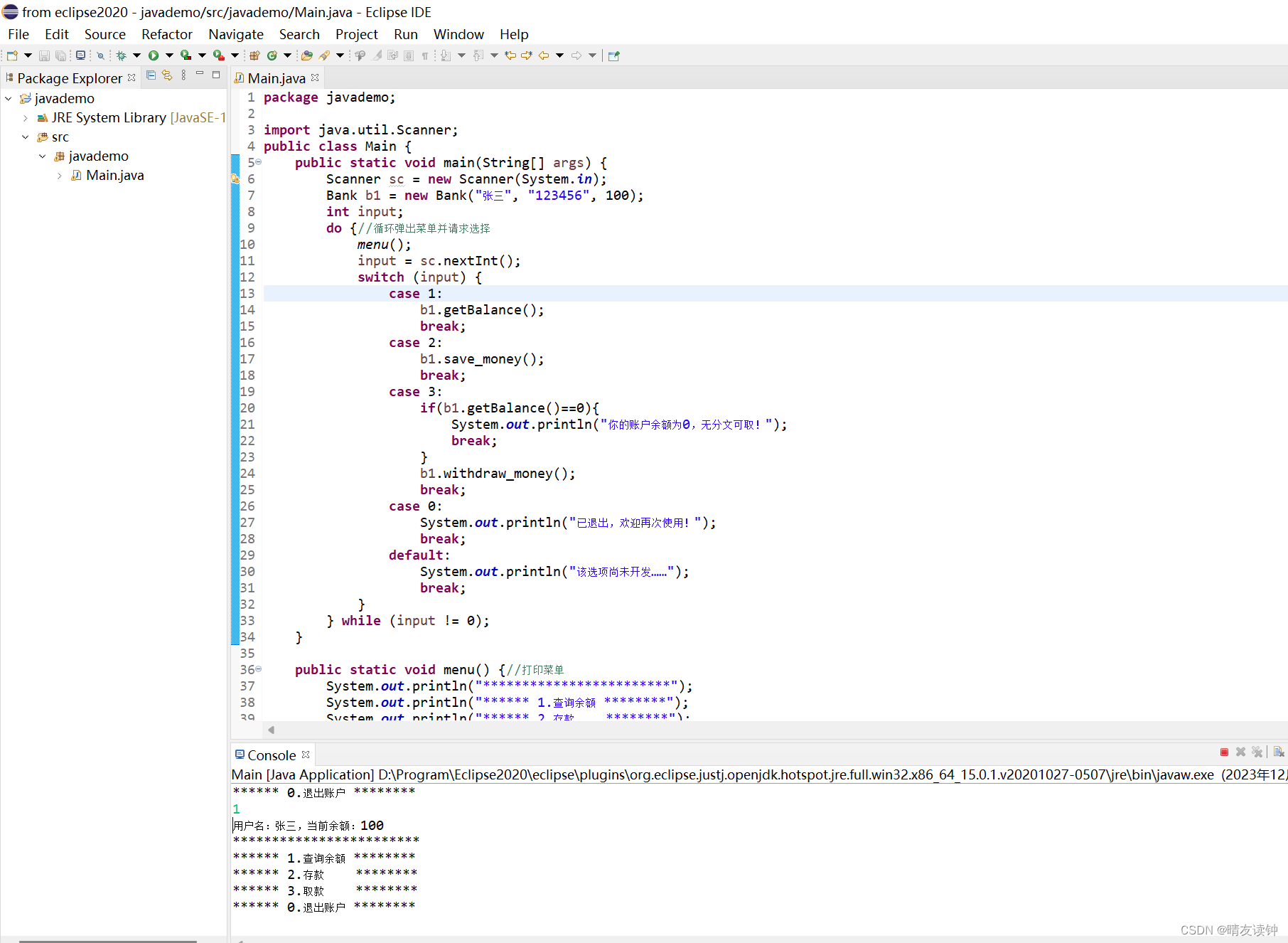
Java期末复习题之封装
点击返回标题->23年Java期末复习-CSDN博客 第1题. 定义一个类Person,定义name和age私有属性,定义有参的构造方法对name和age进行初始化。在测试类中创建该类的2个对象,姓名、年龄分别为lili、19和lucy、20,在屏幕打印出2个对象的姓名和年龄…...
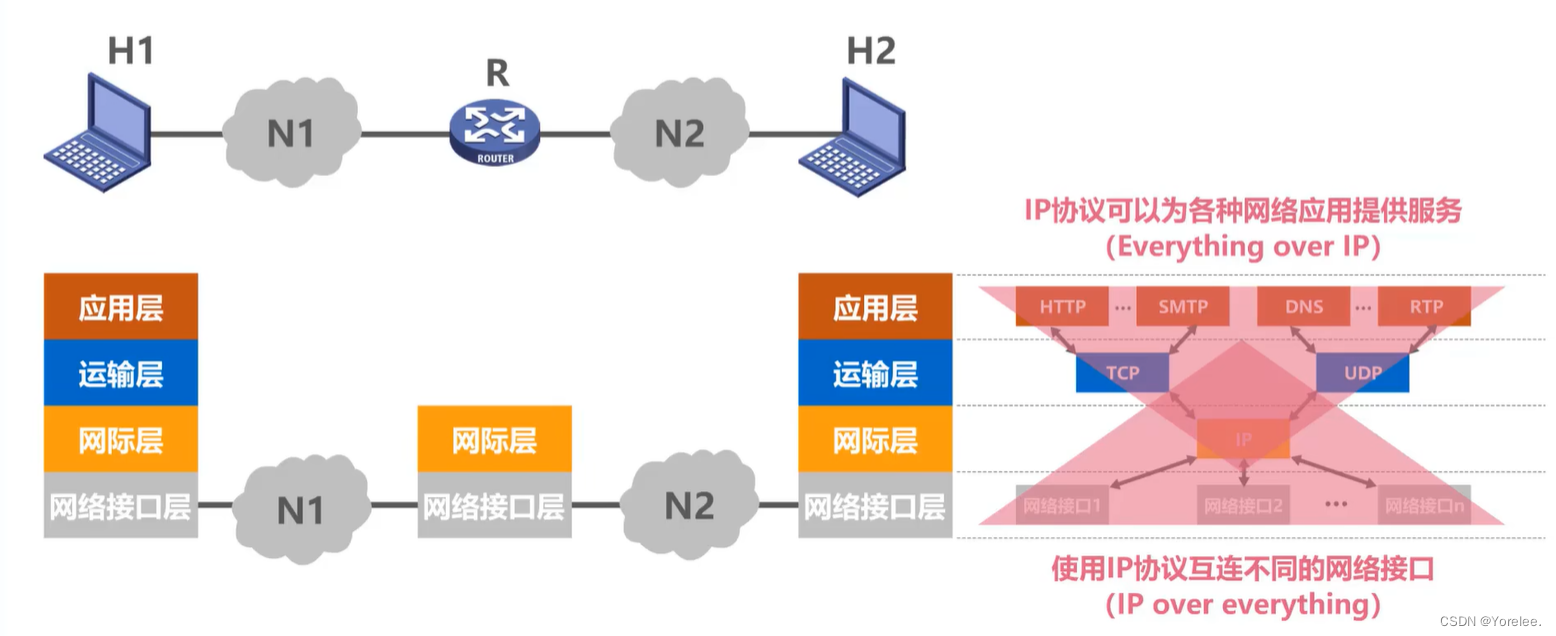
湖科大计网:计算机网络概述
一、计算机网络的性能指标 一、速率 有时候数据量也认为是以10为底的,看怎么好算。(具体吉大考试用什么待商榷) 二、带宽 在模拟信号系统中带宽的含义,本课程中用到的地方是:香农定理和奈奎斯特定理公式的应用之中。 …...

每日一道c语言
任务描述 题目描述:输入10个互不相同的整数并保存在数组中,找到该最大元素并删除它,输出删除后的数组 相关知识(略) 编程要求 请仔细阅读右侧代码,结合相关知识,在Begin-End区域内进行代码补充…...
一些题11)
(C)一些题11
1. #include<stdio.h> #include<string.h> void main() { char *s1"ABCDEF",*s2"aB"; s1; s2; puts(s1); puts(s2); printf("%d\n",strcmp(s1,s2)); } 答案࿱…...

多级路由component页面不加载
项目基于vue-element-admin 新建SubView.vue <template><router-view /> </template><script setup> </script>在父层添加component {path: /sj,component: Layout,redirect: /sj,name: 三级医院评审标准(2022),meta: {title: 三级医院评审标准(…...

【原创】Mac mini M1安装home-brew
Mac mini M1 所需神器 home-brew 按照官网的脚本无法安装。 无奈,从github下载安装包来安装。 Homebrew 结果,还需要先安装 Xcode command 命令行工具 xcode-select --install安装完了,却无法执行。 修改配置文件 cd vi .zshrc添加如下内…...
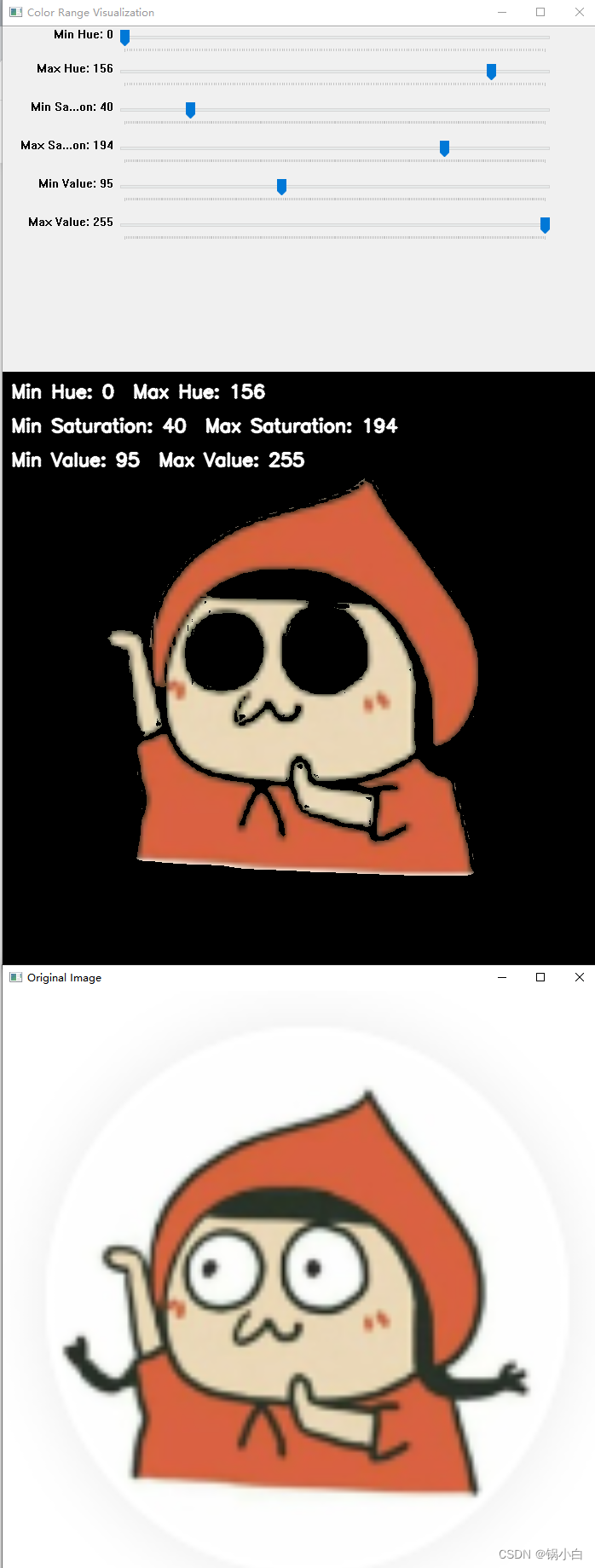
【python交互界面】实现动态观察图像在给定HSV范围的区域显示
HSV颜色空间 与RGB颜色空间相比,HSV颜色空间更适合进行颜色分析和提取特定颜色的目标。在HSV空间中,颜色信息被分布在不同的通道上,使我们能够更准确地定义颜色的范围,并使用阈值操作轻松地分离出我们感兴趣的区域部分。 HSV三个通…...

Vue3中定义变量是选择ref还是reactive?
目录 ref和reactive的优势 1. ref 优势: 应用场景: 示例: 2. reactive 优势: 应用场景: 示例: ref和reactive的劣势 1. ref 2. reactive 应用案例 总结 Vue3中定义变量可以选择使用ref或reac…...
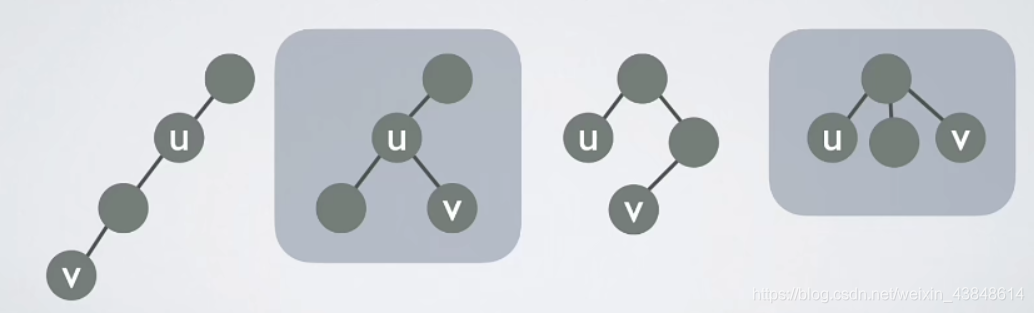
数据结构 | 查漏补缺之哈希表、最短路径、二叉树与森林的转换
哈希表是什么? 或者说 设图采用邻接表的存储结构,写对图的删除顶点和删除边的算法步骤 删除边 删除点 最短路径问题 参考博文 迪杰斯特拉(Dijkstra)算法_dijkstra算法-CSDN博客 Dijkstra(迪杰斯特拉)算法 定义一个点为源点,算源…...
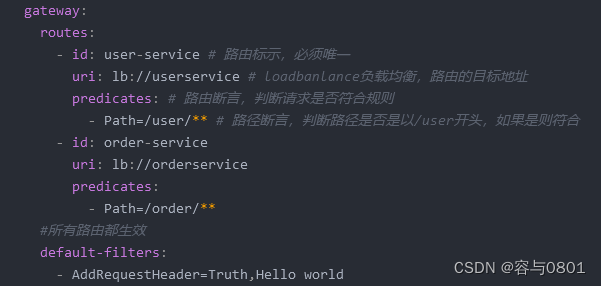
SpringCloud
五大组件 注册/配置中心 Nacos 、Eureka远程调用 Feign负载均衡 Ribbon服务保护 sentinel(实现限流、降级、熔断)网关 gateway 注册中心 Eureka 服务注册:服务提供者把自己的信息注册到Eureka,由Eureka来保存这些信息服务发现…...

fastadmin嵌套关联查询,thinkPHP5嵌套关联查询
fastadmin嵌套关联查询 thinkPHP5嵌套关联查询 笔记记录 嵌套关联查询 A -> B -> C A 表关联B表 B表关联C表 同时把A/B/C表相关的数据展现出来 B表的model B表关联C表 我的C表是B表的自身关联。也是一个表,所以为C表 namespace app…...
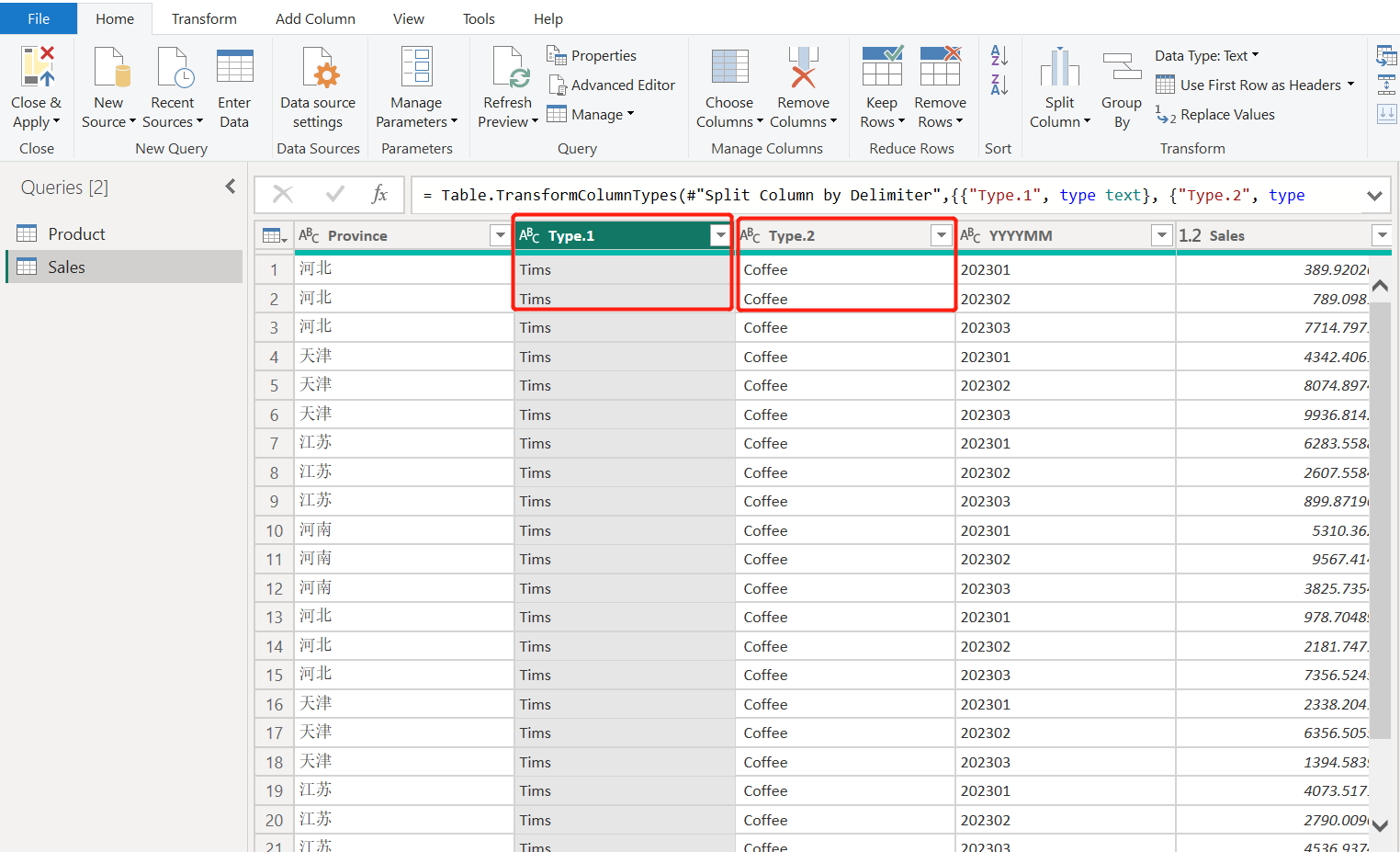
Power BI - 5分钟学习拆分列
每天5分钟,今天介绍Power BI拆分列功能。 什么是拆分列? 有时导入Power BI的数据表中,某列内容都包含同样的特殊字符如 /&/-/_等,可以利用这个特殊字符进行拆分列的操作,获得我们想要的信息。 操作举例…...
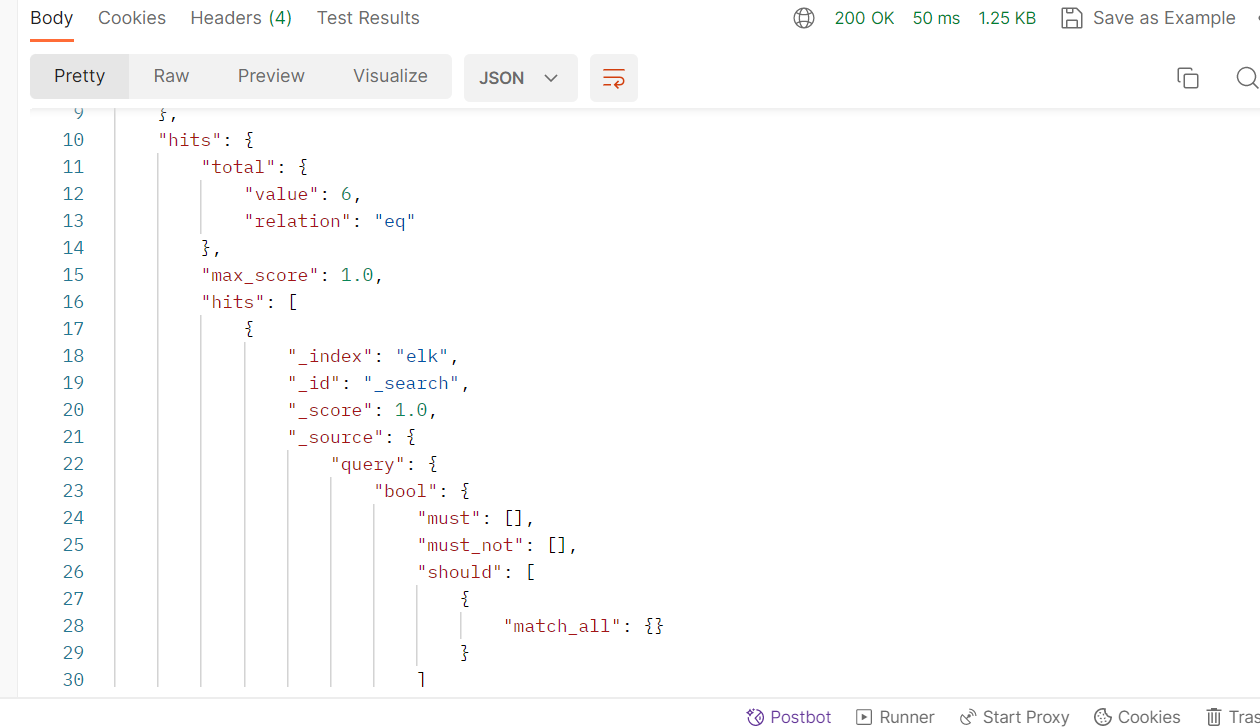
ELK(四)—els基本操作
目录 elasticsearch基本概念RESTful API创建非结构化索引(增)创建空索引(删)删除索引(改)插入数据(改)数据更新(查)搜索数据(id)&…...
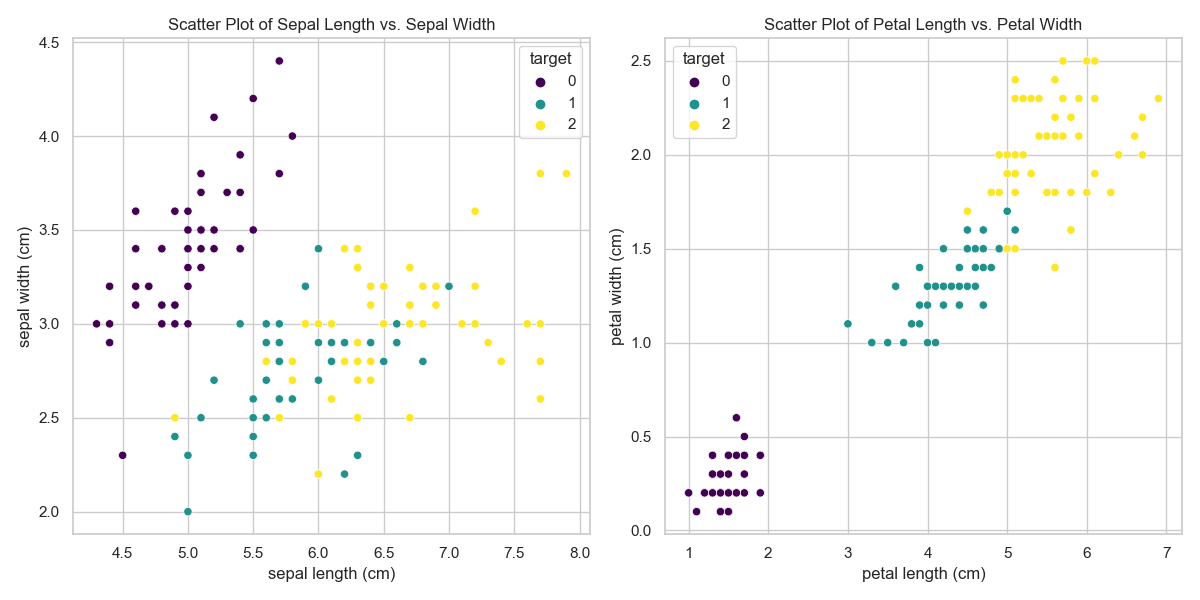
【100天精通Python】Day75:Python机器学习-第一个机器学习小项目_鸾尾花分类项目(上)
目录 1 机器学习中的Helloworld _鸾尾花分类项目 2 导入项目所需类库和鸾尾花数据集 2.1 导入类库 2.2 scikit-learn 库介绍 (1)主要特点: (2)常见的子模块: 3 导入鸾尾花数据集 3.1 概述数据 3.…...
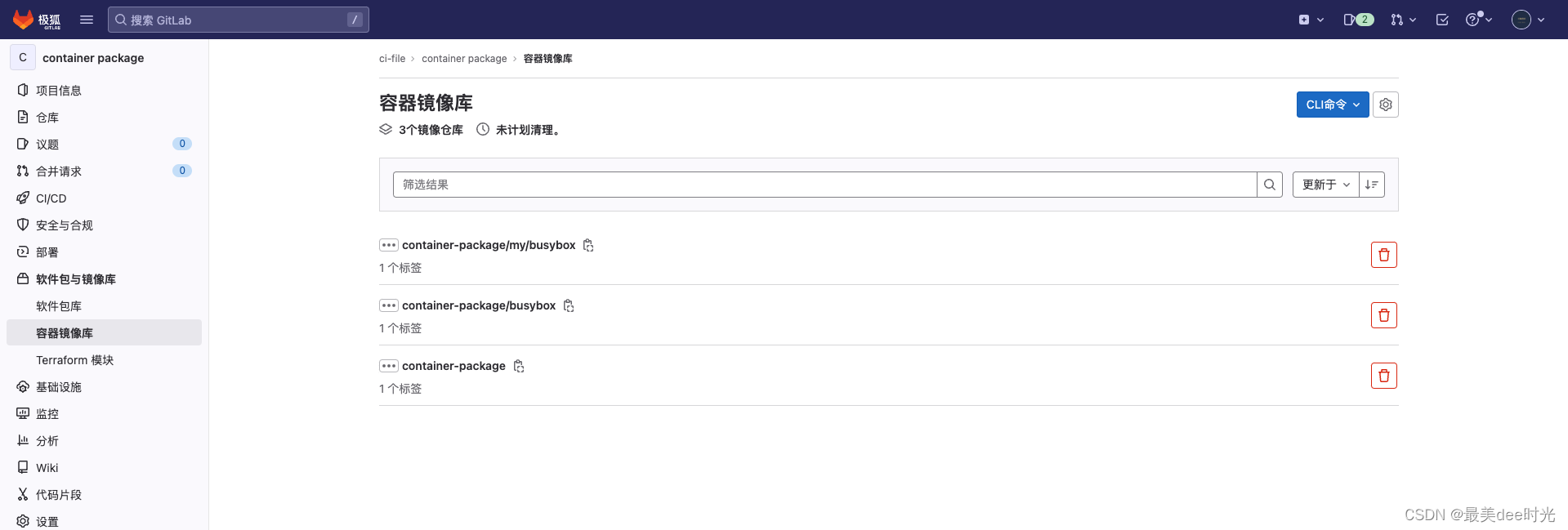
gitlab高级功能之容器镜像仓库
今天给大家介绍一个gitlab的高级功能 - Container Registry,该功能可以实现docker镜像的仓库功能,将gitlab上的代码仓的代码通过docker构建后并推入到容器仓库中,好处就是无需再额外部署一套docker仓库。 文章目录 1. 参考文档2. Container R…...
)
线程的使用(二)
新增实现方式之实现Callable接口 特点 1、可以有返回值。 2、方法可以抛异常。 3、支持泛型的返回值。 4、需借助FutureTask类,比如获取返回值。 步骤 1、创建一个实现Callable接口的实现类。 2、重写call方法, 将此线程需执行的操作声明在call&…...
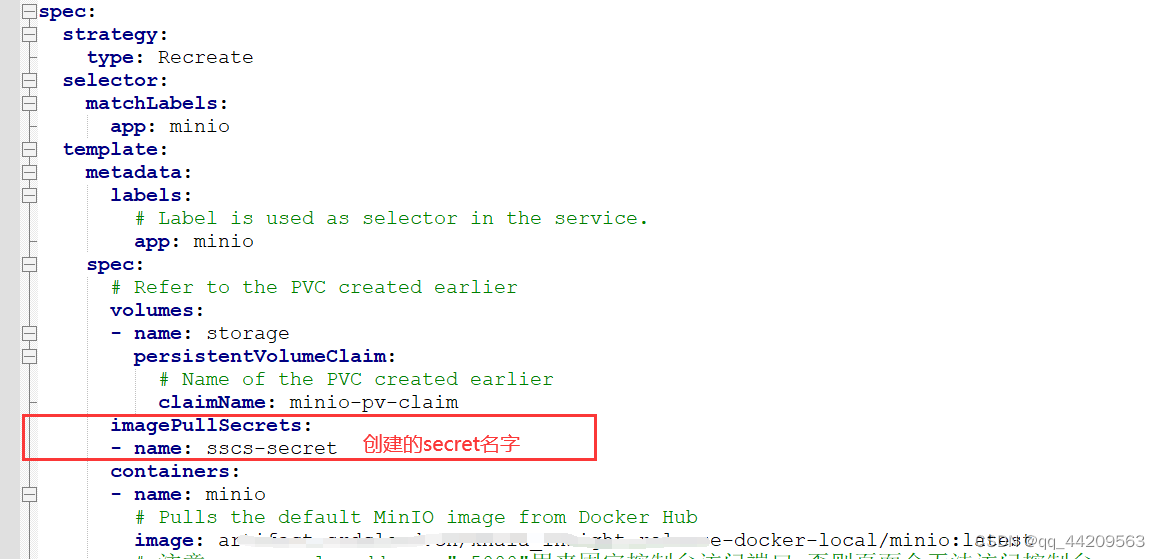
k8s之镜像拉取时使用secret
k8s之secret使用 一、说明二、secret使用2.1 secret类型2.2 创建secret2.3 配置secret 一、说明 从公司搭建的网站镜像仓库,使用k8s部署服务时拉取镜像失败,显示未授权: 需要在拉取镜像时添加认证信息. 关于secret信息,参考: https://www.…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

Linux安全加固:从攻防视角构建系统免疫
Linux安全加固:从攻防视角构建系统免疫 构建坚不可摧的数字堡垒 引言:攻防对抗的新纪元 在日益复杂的网络威胁环境中,Linux系统安全已从被动防御转向主动免疫。2023年全球网络安全报告显示,高级持续性威胁(APT)攻击同比增长65%,平均入侵停留时间缩短至48小时。本章将从…...

shell脚本质数判断
shell脚本质数判断 shell输入一个正整数,判断是否为质数(素数)shell求1-100内的质数shell求给定数组输出其中的质数 shell输入一个正整数,判断是否为质数(素数) 思路: 1:1 2:1 2 3:1 2 3 4:1 2 3 4 5:1 2 3 4 5-------> 3:2 4:2 3 5:2 3…...
——统计抽样学习笔记(考试用))
统计学(第8版)——统计抽样学习笔记(考试用)
一、统计抽样的核心内容与问题 研究内容 从总体中科学抽取样本的方法利用样本数据推断总体特征(均值、比率、总量)控制抽样误差与非抽样误差 解决的核心问题 在成本约束下,用少量样本准确推断总体特征量化估计结果的可靠性(置…...

【Zephyr 系列 16】构建 BLE + LoRa 协同通信系统:网关转发与混合调度实战
🧠关键词:Zephyr、BLE、LoRa、混合通信、事件驱动、网关中继、低功耗调度 📌面向读者:希望将 BLE 和 LoRa 结合应用于资产追踪、环境监测、远程数据采集等场景的开发者 📊篇幅预计:5300+ 字 🧭 背景与需求 在许多 IoT 项目中,单一通信方式往往难以兼顾近场数据采集…...
