蓝桥杯:货物摆放--因数存到数组里的技巧--减少运算量的方法
小蓝有一个超大的仓库,可以摆放很多货物。
现在,小蓝有 n 箱货物要摆放在仓库,每箱货物都是规则的正方体。小蓝规定了长、宽、高三个互相垂直的方向,每箱货物的边都必须严格平行于长、宽、高。
小蓝希望所有的货物最终摆成一个大的长方体。即在长、宽、高的方向上分别堆 L、W、H 的货物,满足 n=L×W×H。
给定 n,请问有多少种堆放货物的方案满足要求。
例如,当 n=4 时,有以下 6种方案:1×1×4、1×2×2、1×4×1、2×1×2、2×2×1、4×1×1
请问,当 n=2021041820210418 (注意有 16 位数字)时,总共有多少种方案?
提示:建议使用计算机编程解决问题。
#include <stdio.h>
int main ()
{long long n=2021041820210418, i, j, count = 0,a[3000], cnt = 0;//找出所有因子放进数组for(int i = 1; i <= sqrt(n); i++){if(n % i == 0){a[++cnt] = i;printf("ys1:%lld ",a[cnt]);if(i*i != n) {a[++cnt] = n/i;printf("ys2:%lld ",a[cnt]);}}}for (i = 1; i <= cnt; i++) {if (n%a[i]==0) {printf("x%lld:%lld\n ",i,a[i]);for (j = 1; j <= cnt; j++) {if ((n/a[i])%a[j]==0) {printf("y%lld:%lld ",j,n/a[j]);count++;}}}}printf("\n总个数为%lld",count);
}```相关文章:

蓝桥杯:货物摆放--因数存到数组里的技巧--减少运算量的方法
小蓝有一个超大的仓库,可以摆放很多货物。 现在,小蓝有 n 箱货物要摆放在仓库,每箱货物都是规则的正方体。小蓝规定了长、宽、高三个互相垂直的方向,每箱货物的边都必须严格平行于长、宽、高。 小蓝希望所有的货物最终摆成一个大…...

我的创作纪念日——一年
机缘 初心始于对技术的热爱和分享知识的渴望。最初,我在一次练习中遇到了一些问题,通过解决这些问题并将解决方案记录下来,我意识到分享经验对自己和他人都非常有价值。于是,我开始在博客和社交平台上记录日常学习过程、撰写技术…...
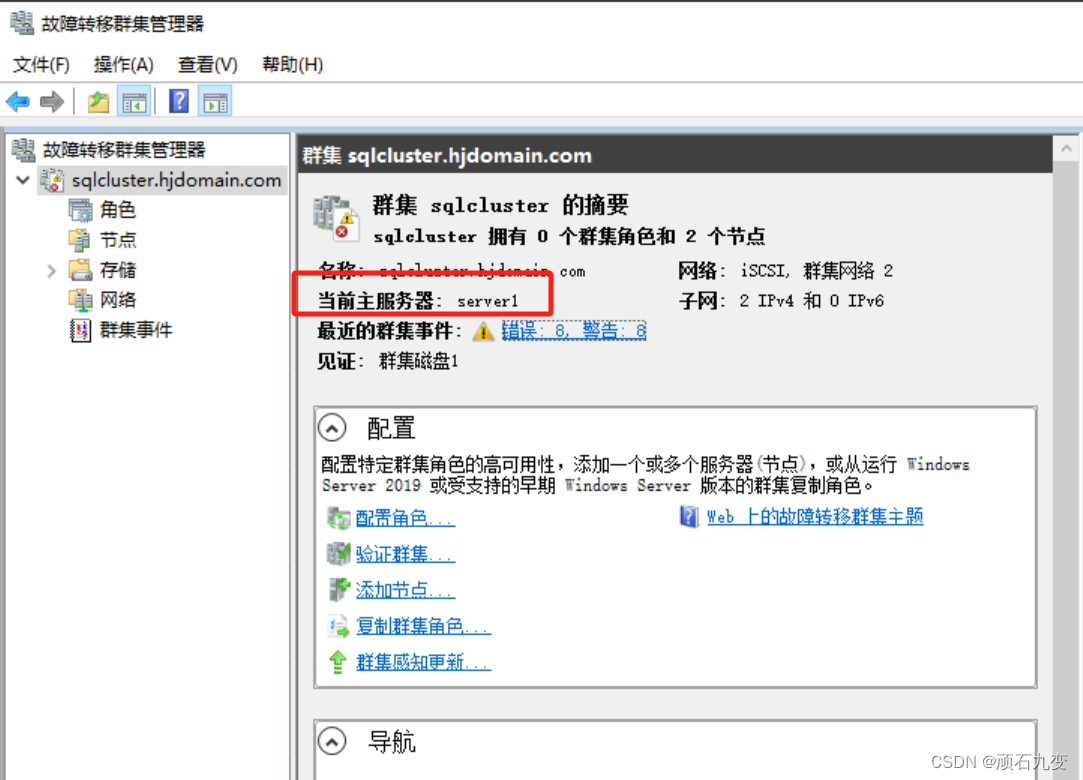
Windows server 部署iSCSI共享磁盘搭建故障转移群集
在域环境下,在域控制器中配置iSCSI服务,配置共享网络磁盘,在节点服务器使用共享磁盘,并在节点服务器中搭建故障转移群集,实现故障转移 环境准备 准备3台服务器,配置都是8g2核,50g硬盘…...
2023年山东省职业院校技能大赛信息安全管理与评估二三阶段样题
2023年山东省职业院校技能大赛信息安全管理与评估二三阶段 样题 第二阶段 模块二 网络安全事件响应、数字取证调查、应用程序安全 一、竞赛内容 Geek极安云科专注技能竞赛技术提升,基于各大赛项提供全面的系统性培训,拥有完整的培训体系。团队拥有曾…...

数据结构——栈与栈排序
栈的特性 栈是一种遵循后进先出(LIFO)原则的数据结构。其基本操作包括: push:将元素添加到栈顶。pop:移除栈顶元素。peek:查看栈顶元素,但不移除。 栈排序的原理 栈排序的核心是使用两个栈&…...
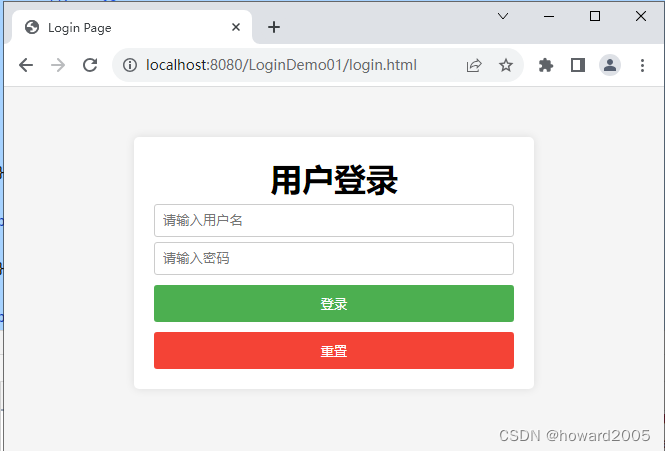
Java Web应用小案例 - 实现用户登录功能
文章目录 一、使用纯JSP方式实现用户登录功能(一)项目概述(二)实现步骤1、创建Web项目2、创建登录页面 二、使用JSPServlet方式实现用户登录功能三、使用JSPServletDB方式实现用户登录功能 一、使用纯JSP方式实现用户登录功能 &a…...
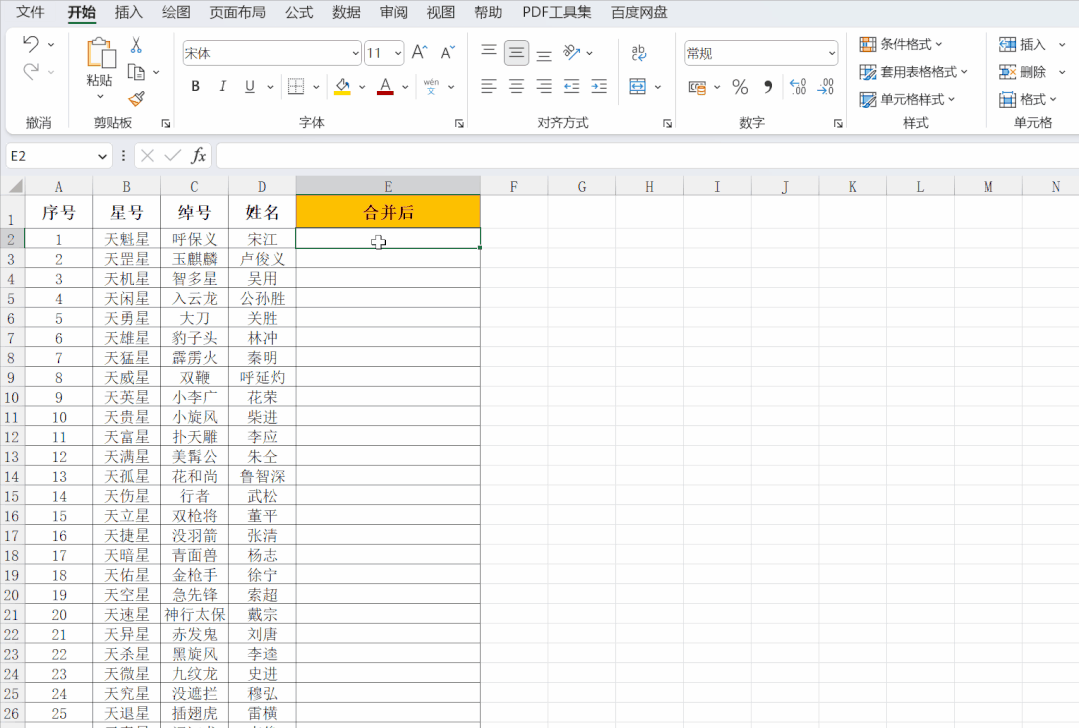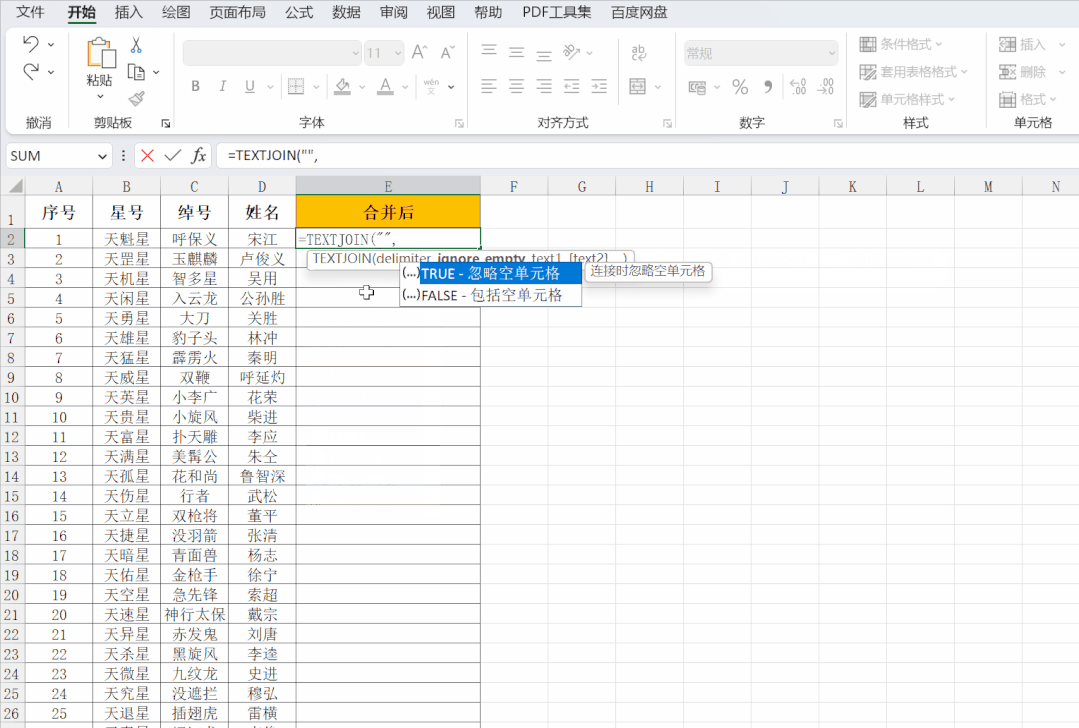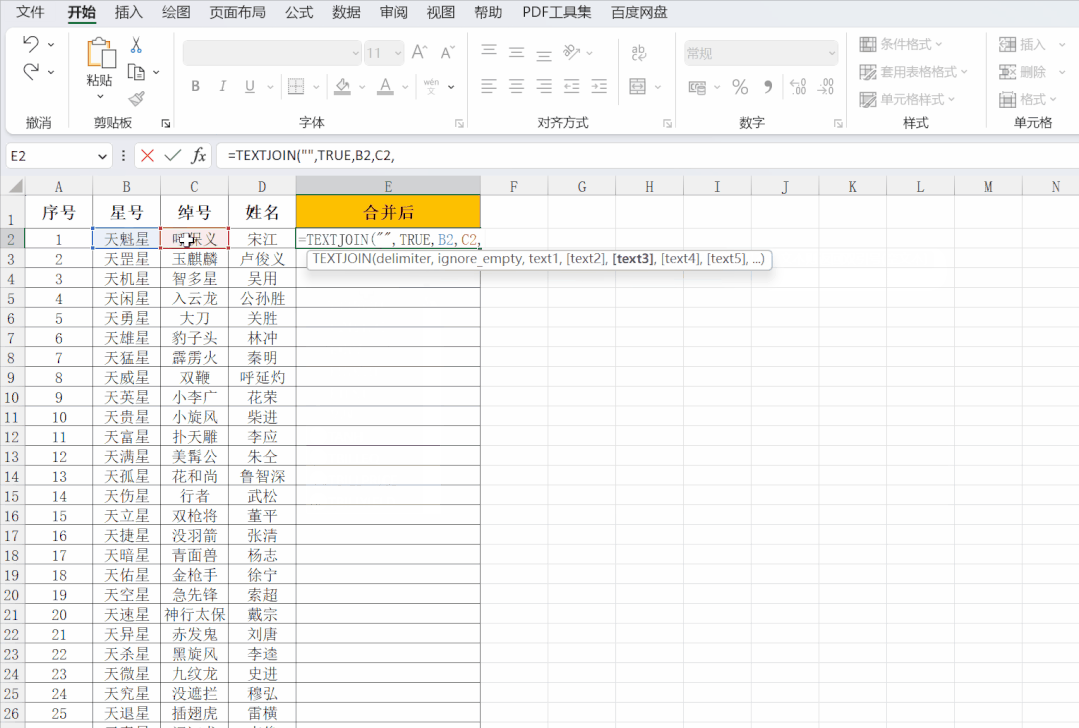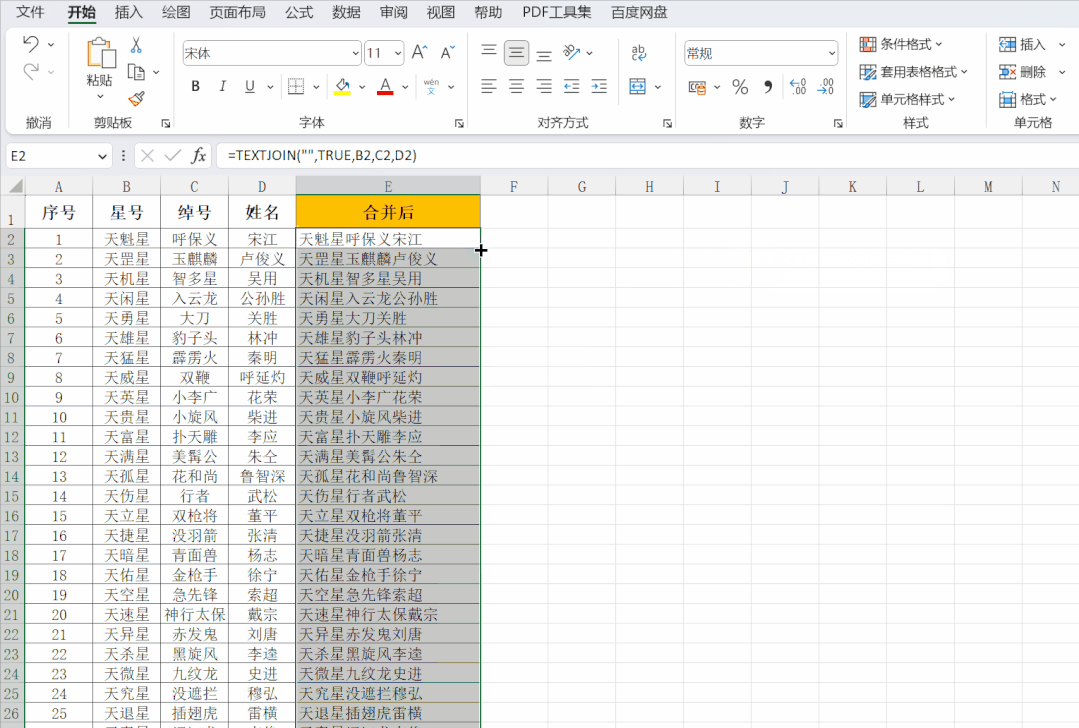
Excel——多列合并成一列的4种方法
Excel怎么将多列内容合并成一列? 怎么将多个单元格的内容连接起来放在一个单元格里? 比如下图,要将B、C、D列的内容,合并成E列那样,该怎么做呢? △图1 本文中,高潜老师将给大家介绍 4种 将多…...
路由)
Vue笔记(四)路由
路由(Vue Router) 用Vue Vue Router创建单页面应用非常简单。当加入Vue Router时,需要将组件映射到路由上,让Vue知道在哪里渲染它们。 路由基本例子 <!-- 引入Vue 和 router --><script src"https://unpkg.com/vu…...
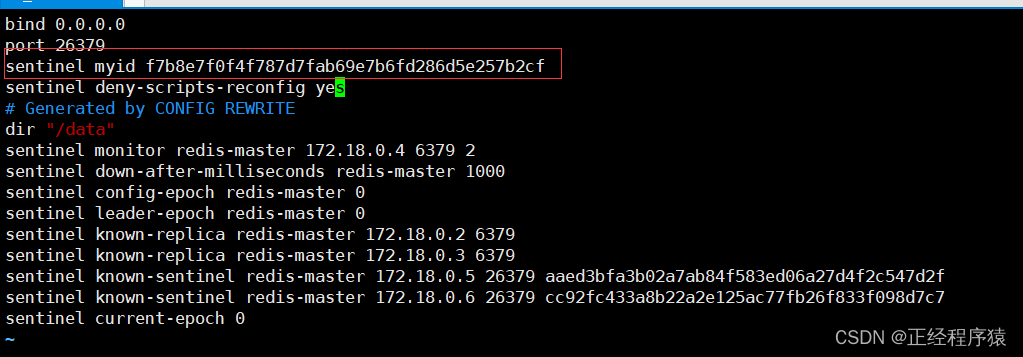
Redis部署-哨兵模式
目录 redis sentinel相关名词 redis sentinel架构 故障转移流程 基于docker搭建redis哨兵 准备工作 搭建过程 模拟主节点宕机,观察哨兵节点的工作流程 哨兵重新选取主节点的流程 1.主观下线 2.客观下线 3.哨兵节点推举出一个leader节点 4.leader选举完毕,leader挑选…...
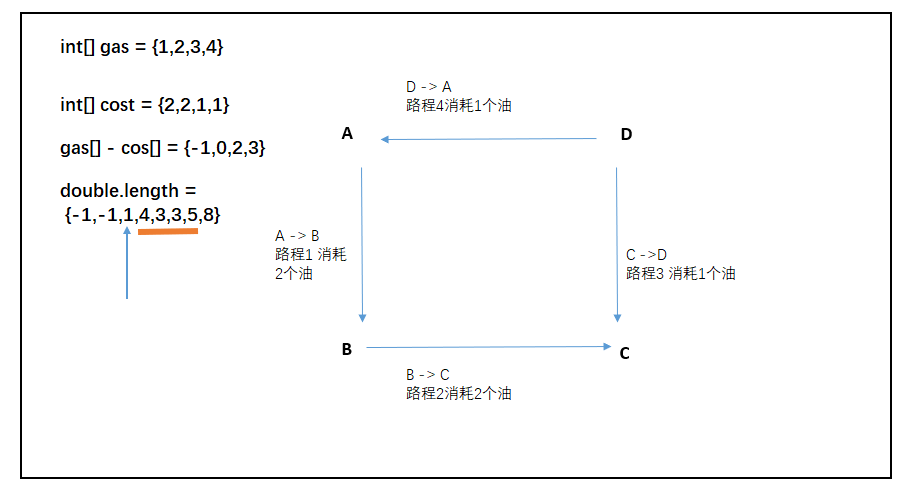
滑动窗口练习(三)— 加油站问题
题目 测试链接 在一条环路上有 n 个加油站,其中第 i 个加油站有汽油 gas[i] 升。 你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。 给定两个整数数组…...
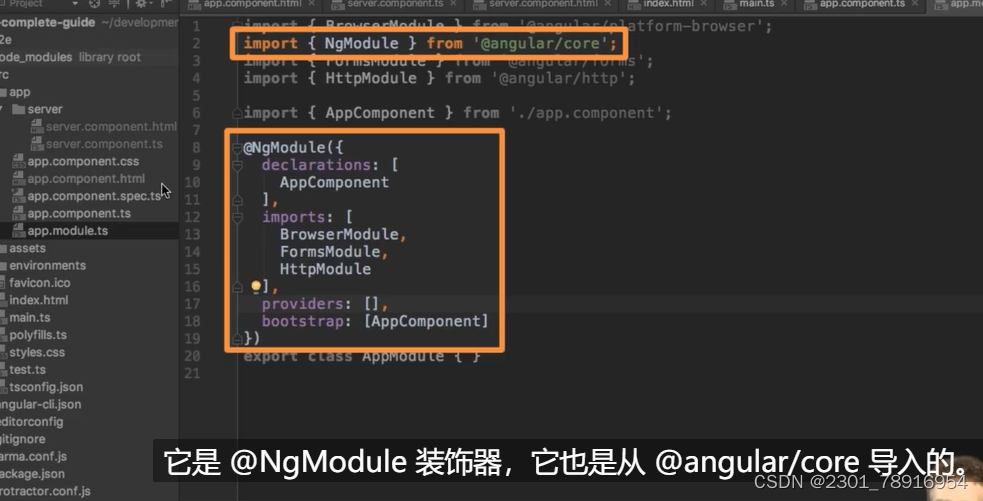
udemy angular decoration 自存
番外 为什么一个ts文件变成了component,因为它使用了components装饰器 components is just a class,you export it so angular know how to use it 举例:组件装饰器 decoration前总是有一个符号 decoration的作用(之一?) NgModu…...
msvcr90.dll丢失的解决方法分享,5个快速修复dll文件丢失教程
在今天的电脑使用过程中,我们可能会遇到各种各样的问题。其中之一就是msvcr90.dll丢失的问题。那么,msvcr90.dll是什么?msvcr90.dll丢失对电脑有什么影响?又该如何解决这个问题呢?接下来,我将为大家详细介绍…...

海外媒体发稿:软文发稿推广技巧解析超级实用-华媒舍
随着互联网时代的发展,软文发稿成为推广产品与服务的重要手段之一。本文将向大家介绍软文发稿推广的技巧,帮助您更好地利用软文推广商业活动。无论是拥有自己的品牌还是个人创业者,都可以从中受益。 1. 什么是软文? 软文是指以文…...
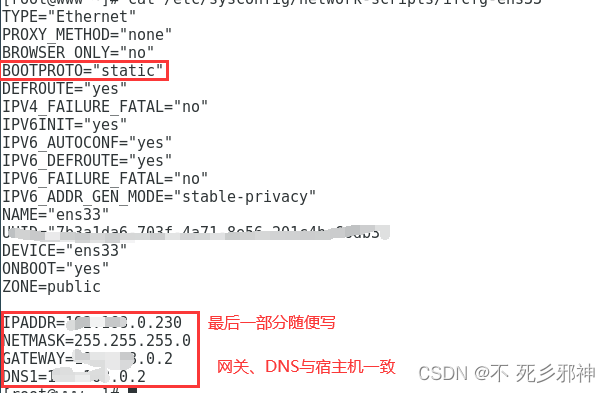
vm net 方式 静态ip配置访问主机IP和外网
1、win 11 安装vm,镜像文件 F:\software\VMwork\CentOS-7-x86_64-Everything-1804.iso 2、配置网络 net 方式 3、右击网络--》属性---》更改适配器设置--》vmnet8 属性、这里不做配置会出现主机ping通访问不通的情况,(访问不通,…...
基本语法)
Vue笔记(二)基本语法
基本语法 <style> table {border-collapse: collapse;margin:0 auto; } strong {color: rgb(235, 51, 100); }td, th {padding-left: 6px; } table tr td:first-child {width:150px } table tr td:nth-child(2) {width:300px } </style> <template><tabl…...
)
前端面试提问(4)
1、手撕防抖与节流、树与对象的转换、递归调用,链表头插法 1.1、防抖 防抖函数用于延迟执行某个函数,直到过了一定的间隔时间(例如等待用户停止输入)后再执行。 即后一次点击事件发生时间距离一次点击事件至少间隔一定时间。 …...
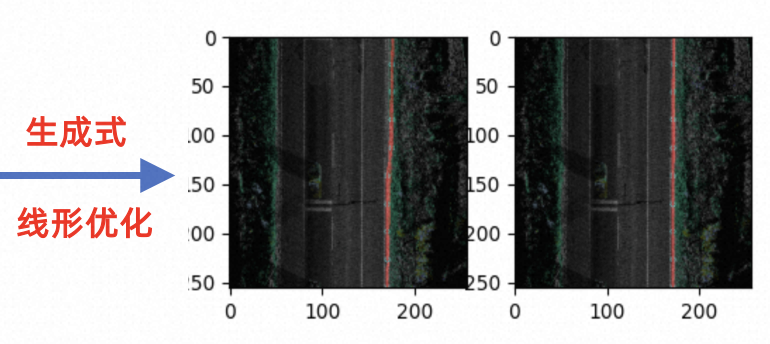
基于BEV+Transformer的地面要素感知+建模技术在高德的应用
导读 本文将主要介绍BEVTransformer端到端感知与建模技术在高德各项业务中的应用,如高精地图中地面要素(包含线要素和地面标识)自动化上的具体方案及其演化过程。该方案使用BEVTransformer技术来实现采集车上不同传感器(包含激光和…...

了解c++11中的新增
一,统一的初始化列表 在引入c11后,我们得出计划都可以用初始化列表进行初始化。 C11 扩大了用大括号括起的列表 ( 初始化列表 ) 的使用范围,使其可用于所有的内置类型和用户自 定义的类型, 使用初始化列表时,可添加等…...
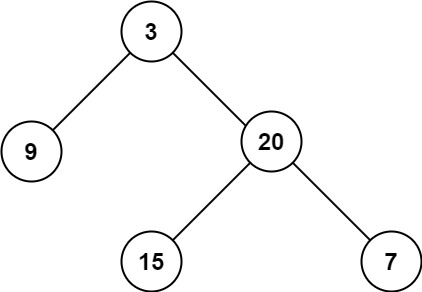
104. 二叉树的最大深度(Java)
目录 解法: 官方解答: 方法一:深度优先搜索 方法二:广度优先搜索 思路与算法 复杂度分析 时间复杂度: 空间复杂度: 给定一个二叉树 root ,返回其最大深度。 二叉树的 最大深度 是指从根…...

SpringSecurity6 | 自定义认证规则
✅作者简介:大家好,我是Leo,热爱Java后端开发者,一个想要与大家共同进步的男人😉😉 🍎个人主页:Leo的博客 💞当前专栏: Java从入门到精通 ✨特色专栏…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...
